基于兒童立場的小學(xué)數(shù)學(xué)練習(xí)設(shè)計新探

周云霞 黃 芬

（江陰市利港實驗小學(xué)，江蘇無錫 214400）

基于兒童立場的小學(xué)數(shù)學(xué)練習(xí)設(shè)計，即在教學(xué)中，以兒童為本，以兒童學(xué)習(xí)為中心，基于兒童的起點，著眼兒童的發(fā)展，充分尊重兒童真實的認(rèn)識過程，從學(xué)的視角設(shè)計練習(xí)，給兒童平添學(xué)習(xí)和建構(gòu)的機會，讓兒童的思維在有效的練習(xí)中悄然生長。

一、基于兒童的個體差異彈性設(shè)計練習(xí)

數(shù)學(xué)課標(biāo)中明確指出：數(shù)學(xué)課程要面向全體學(xué)生，適應(yīng)學(xué)生個性發(fā)展的需要，使得人人都能獲得良好的數(shù)學(xué)教育，不同的人在數(shù)學(xué)上得到不同的發(fā)展。因此，數(shù)學(xué)練習(xí)設(shè)計，要面向全體兒童，關(guān)注兒童的個體差異，促進每一個兒童在原有基礎(chǔ)上得到發(fā)展，也就是有差異的發(fā)展。

1.擬定彈性目標(biāo)

在一個班級中，我們要承認(rèn)并重視此類現(xiàn)象：一部分學(xué)生往往會走得快一些，一部分學(xué)生則會走得慢一些。設(shè)計練習(xí)時，我們要充分考慮兒童之間的差異，擬定彈性教學(xué)目標(biāo)。如“公倍數(shù)和最小公倍數(shù)”第一課時的教學(xué)，教學(xué)目標(biāo)可定為：全班學(xué)生理解公倍數(shù)和最小公倍數(shù)的含義；部分學(xué)生學(xué)會用一一列舉的方法找到兩個數(shù)的最小公倍數(shù)；部分學(xué)生則在一一列舉的方法的基礎(chǔ)上，發(fā)現(xiàn)用“大數(shù)翻倍”的方法找出兩個數(shù)的最小公倍數(shù)。總之，基于學(xué)生實際擬定的教學(xué)目標(biāo)，應(yīng)當(dāng)在學(xué)生的“最近發(fā)展區(qū)”內(nèi)，是有彈性與差異性的。

2.設(shè)計開放問題

開放題，思考起點低，所有學(xué)生都能投入思考，具有較大的思維空間，不同的學(xué)生會有多樣的思考，都會有較大的進步與收獲。如一年級“元角分的認(rèn)識”練習(xí)時，設(shè)計：“小剛有一張5角紙幣，五張2角紙幣，八張1角紙幣，他要拿一元去買雪糕，他可以怎么拿？”這是一道開放題，學(xué)生解答有時會出現(xiàn)多種答案：有少數(shù)后進生有一種方法；大多數(shù)學(xué)生能夠列幾種甚至全部拿法；還有個別能力強的學(xué)生不僅能全部列出，而且能使自己的拿法條理化，體現(xiàn)一定邏輯順序。同學(xué)之間通過交流相互補充、修正，全員參與，使每位學(xué)生都能獲得新的認(rèn)識。

3.設(shè)計層次練習(xí)

練習(xí)時，還可以由易到難設(shè)計不同層次的習(xí)題，可以設(shè)計“必做題”和“選做題”，必做題是基礎(chǔ)題，每個學(xué)生都要做的，但是選做題，讓學(xué)生根據(jù)自身的能力選擇做題，這樣就能保證每個學(xué)生“吃得了”又“吃得飽”。總之，每一位學(xué)生在原有基礎(chǔ)上得到發(fā)展，都能體會到成功的快樂。

二、基于兒童的認(rèn)知特點靈活安排練習(xí)

數(shù)學(xué)教材上占據(jù)了教材過半篇幅的練習(xí)，為練習(xí)課提供了很好的練習(xí)線索，但大多數(shù)教師照本宣科，大大降低了練習(xí)的效果。教學(xué)時，教師要根據(jù)兒童的認(rèn)知特點，選擇好教學(xué)內(nèi)容，靈活安排，使教學(xué)的出發(fā)點與落腳點都是為了兒童的發(fā)展。

1.教材練習(xí)變一變

在教學(xué)時，根據(jù)兒童在學(xué)習(xí)過程中的實際情況，按照兒童的年齡特點和認(rèn)知特點組織練習(xí)，對教材題目進行增、刪、換等調(diào)整，從而使題目的設(shè)計更貼近兒童的學(xué)習(xí)實際，充分激發(fā)兒童學(xué)習(xí)積極性，讓練習(xí)更具有實效。

如二年級下冊“認(rèn)識平均分”教材后的練習(xí)：1.動手平均分12根小棒；2.判斷哪種是平均分；3.先圈再填空；4.解決實際問題。“平均分”這個概念對于二年級學(xué)生來說較抽象，最后解決實際問題時還存在問題。根據(jù)學(xué)生的學(xué)習(xí)認(rèn)知規(guī)律，我將練習(xí)調(diào)整如下：1.概念判斷，加深認(rèn)識；2.動手圈分，在操作中加深理解；3.增加“無圖想象平均分”練習(xí)，幫助學(xué)生抽象“平均分”概念，解決實際問題；4.開放題練習(xí)，發(fā)散學(xué)生的思維。通過重新調(diào)整練習(xí)內(nèi)容，學(xué)生從形象思維逐步過渡到抽象思維，不僅加深認(rèn)識，內(nèi)化認(rèn)知，又發(fā)展了思維。

2.學(xué)生錯題用一用

在教學(xué)時，我們要關(guān)注學(xué)生在學(xué)習(xí)過程中產(chǎn)生的學(xué)習(xí)錯誤，并看到錯誤背后隱含的合理因素，幫助學(xué)生在糾正錯誤中學(xué)會知識，積極采取措施使“錯誤”轉(zhuǎn)變?yōu)榇龠M理解的有效契機。在四年級學(xué)習(xí)了“運算律”后，從課堂作業(yè)發(fā)現(xiàn)，學(xué)生乘法分配律和乘法結(jié)合律容易混淆，如：

88×125=（80+8）×125=80×（8×125）

88×125=8×11×125=（8×125）×（11×125）

在練習(xí)課上，我用視頻展示學(xué)生在簡算時的錯誤，讓學(xué)生議一議，說一說錯在哪，怎么改，以后要注意什么。這樣呈現(xiàn)題目，也就是吸納了學(xué)生學(xué)習(xí)過程中的想法，從而使練習(xí)的題目更加鮮活，更具有針對性。

三、基于兒童的思維發(fā)展專項設(shè)計練習(xí)

數(shù)學(xué)課標(biāo)指出：“數(shù)學(xué)教學(xué)活動，特別是課堂教學(xué)應(yīng)激發(fā)學(xué)生興趣，調(diào)動學(xué)生積極性，引發(fā)學(xué)生的數(shù)學(xué)思考，鼓勵學(xué)生的創(chuàng)造性思維。”數(shù)學(xué)練習(xí)，比練更重要的是思。不要將練習(xí)單純作為“程序性練習(xí)”，而應(yīng)當(dāng)讓學(xué)生徜徉于數(shù)學(xué)思考中，使學(xué)生的思維得到發(fā)展。

1.設(shè)計對比練習(xí)

數(shù)學(xué)教學(xué)中，教師可以根據(jù)新舊知識間的聯(lián)系，通過形式、內(nèi)容、方法等對比設(shè)計練習(xí)，引導(dǎo)學(xué)生抓住其間的聯(lián)系，辨別其中的差異，以此加深理解，提高學(xué)生的分析能力，豐富學(xué)生知識結(jié)構(gòu)，培養(yǎng)學(xué)生良好學(xué)習(xí)習(xí)慣。

如一年級“兩位數(shù)加一位數(shù)（進位加）”這節(jié)課，主要是讓學(xué)生掌握“個位相加滿十，十位多1”的算理與算法，我設(shè)計了這樣的專項對比練習(xí)：“42+6幾十多？42+9幾十多？”使兒童在對比中強化進位；“26+9=46+9=76+9=86+9=”學(xué)生在這樣的求同和求異對比中，明晰了自己的思維，清晰地理解了進位加的算理。

2.設(shè)計延伸練習(xí)

數(shù)學(xué)練習(xí)要善于挖掘知識內(nèi)部的聯(lián)系，恰當(dāng)對所學(xué)知識進行延伸和拓展。精心設(shè)計延伸練習(xí)，幫助兒童感知新舊知識間的聯(lián)系，并把新知納入原有知識體系，鞏固新知，拓展思維，促進知識的遷移。

如教學(xué)二年級“認(rèn)識分米和毫米”這一課時，最后設(shè)計了填長度單位練習(xí)：芝麻寬2（），橡皮長2（ ），文具盒長2（ ），小樹高2（ ）。通過填不同的長度單位，引出學(xué)生所有學(xué)過的長度單位，幫助學(xué)生把新舊知識進行鏈接，將本節(jié)課內(nèi)容納入原有知識體系，實現(xiàn)認(rèn)知體系的新建構(gòu)。

3.設(shè)計挑戰(zhàn)練習(xí)

數(shù)學(xué)新課標(biāo)中指出“創(chuàng)新意識的培養(yǎng)是現(xiàn)代數(shù)學(xué)教學(xué)的基本任務(wù)，應(yīng)體現(xiàn)在數(shù)學(xué)教與學(xué)的過程中”。在教學(xué)中，對教學(xué)內(nèi)容做適當(dāng)加工，設(shè)計一些挑戰(zhàn)性的練習(xí)，讓數(shù)學(xué)練習(xí)的過程成為學(xué)生經(jīng)歷探索、獲得發(fā)現(xiàn)的歷程，可以激發(fā)學(xué)生主動思考，提高學(xué)生思維的參與度，培養(yǎng)學(xué)生的創(chuàng)新思維。

如在“圓的練習(xí)”這節(jié)練習(xí)課教學(xué)時，我一開始讓男女生分別計算大圓和小圓的周長和面積（如圖1）；然后把兩圖組合成圓環(huán)，讓學(xué)生計算圓環(huán)的面積。

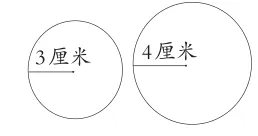
圖1

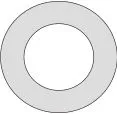
圖2

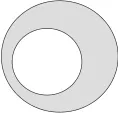
圖3

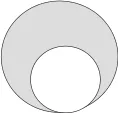
圖4

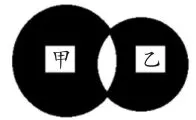
圖5

在此基礎(chǔ)上，出示變化題（圖3、圖4），部分學(xué)生通過計算與對比，很快發(fā)現(xiàn)了只要小圓在大圓里面，無論小圓的位置怎樣改變，陰影部分形狀雖變了，但面積大小不變。趁熱打鐵，進一步探索圖5中兩個圓組合圖形中的陰影部分面積，再次讓學(xué)生思維高漲，創(chuàng)造性思維由此迸發(fā)。

有效的教育始于對兒童的理解，有效的習(xí)題設(shè)計也一定是始于對兒童的理解。數(shù)學(xué)練習(xí)，不只是指向知識的鞏固、能力的提高，更應(yīng)該是集中指向兒童的發(fā)展，為兒童持續(xù)發(fā)展打下良好的基礎(chǔ)。數(shù)學(xué)練習(xí)，教師要讓學(xué)生回歸主體的地位，讓學(xué)生練得有趣，練得有味，練習(xí)有勁，練得有效！

[1]中華人民共和國教育部.義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）[S].北京:北京師范大學(xué)出版社,2011.

[2]曹才翰，章建躍.數(shù)學(xué)教育心理學(xué)[M].北京：北京師范大學(xué)出版社，2006.

[3]賁友林.現(xiàn)場與背后[M].南京:江蘇教育出版社,2004.

[4]余文森.小學(xué)數(shù)學(xué)：名師高效教學(xué)設(shè)計藝術(shù)[M].重慶:西南師范大學(xué)出版社,2010.