高速電磁閥靜態電磁力數學模型

趙建輝， 格列霍夫·雷奧尼德， 范立云， 馬修真， 宋恩哲

(1.哈爾濱工程大學 動力與能源工程學院，黑龍江 哈爾濱 150001； 2.莫斯科國立鮑曼技術大學 機械制造學院，俄羅斯 莫斯科 115569)

共軌噴油器是高壓共軌系統關鍵部件，直接影響噴油量波動、噴嘴內燃油的氣液兩相流動特性、缸內燃油霧化特性和油氣混合質量。高速電磁閥是共軌噴油器的核心控制部件，高動態響應特性的高速電磁閥有利于提高共軌系統對循環噴油量、噴油定時和噴油規律的控制精度。

電磁力特性和運動件的質量共同決定高速電磁閥動態響應特性，電磁力特性比運動件的質量對高速電磁閥動態響應的影響更為顯著，因此大量文獻報道了高速電磁閥靜態電磁力的研究。Liu、Sun等[1-2]采用三維有限元方法，以電控單體泵上的高速電磁閥為研究對象，開展高速電磁閥結構參數對靜態電磁力影響規律的研究。Cheng、Miller等[3-4]采用有限元法進行高速電磁閥靜態電磁力優化研究，獲得了最優的電磁閥結構參數。在采用三維有限元法進行高速電磁閥設計優化時，其較長的求解時間使得設計工作效率下降。更為重要的是，共軌噴油器內高速電磁閥的工作過程涉及電磁、機械和液力的非線性瞬變耦合，電磁三維有限元法很難實現高速電磁閥的多物理場瞬變耦合計算。在研究電控高壓共軌系統時，許多學者采用的是一維靜態電磁力子模型與機械子模型、液力子模型耦合的研究方法開展相關科研工作[5-8]。高速電磁閥一維靜態電磁力數學模型的重要性不僅體現在電磁閥電磁轉化特性研究，更體現在電磁閥多物理場耦合的動態響應特性研究。Topcu等[9-11]在建立電磁閥一維數學模型時，認為電磁閥軟磁材料的磁阻和氣隙磁阻相比較小，在建模時可忽略電磁閥軟磁材料的磁阻，即不考慮電磁力的飽和現象。Sefkat等[12]在建立電磁數學模型時假設磁場是單調變化的，即磁場是不存在磁場飽和現象。然而，大量的研究結果表明，在共軌噴油器工作過程中，高速電磁閥必然產生電磁力飽和，尤其是在高驅動電流條件下。

綜合以上，在高速電磁閥靜態電磁力數學模型建立時，是需要考慮最大電磁力飽和這一現象，磁飽和現象不需要被考慮的這一不適當的假設條件會嚴重降低電磁閥在電磁轉化預測方面的預測準確性。因此，本文根據高速電磁閥電磁瞬變耦合原理，以磁性材料的瞬態磁導率為橋梁，建立了考慮最大電磁力飽和的高速電磁閥靜態電磁力數學模型。

1 高速電磁閥電磁力數學模型

1.1 高速電磁閥電路-磁路模型

圖1所示為高速電磁閥的結構示意圖，高速電磁閥主要由鐵芯、線圈和銜鐵組成，為實現高速電磁閥大的電磁力，鐵芯和銜鐵通常是采用飽和磁感應強度大、剩磁小的軟磁材料制造。

在高速電磁閥中，電磁閥總磁通和磁路總磁阻之間的關系為

(1)

式中：Φ為總的磁通量，N為線圈匝數，I為電流，Rtotal為電磁閥總磁阻。

為實現高速電磁閥電磁數學模型可以正確描述非線性磁化過程和磁飽和現象，電磁閥數學模型必須考慮電磁閥鐵芯和銜鐵等軟磁材料的磁阻。此外，通常情況下，電磁閥的主副磁極對應的等效橫截面積是不同的，為了使數學模型能夠描述這種現象，把主副磁極對應的氣隙磁阻分為用Rgap1和Rgap2表示。在電磁閥的計算過程中，忽略高速電磁閥氣隙處的邊緣效應和電磁閥的漏磁。圖2所示為高速電磁閥的等效磁路示意圖。

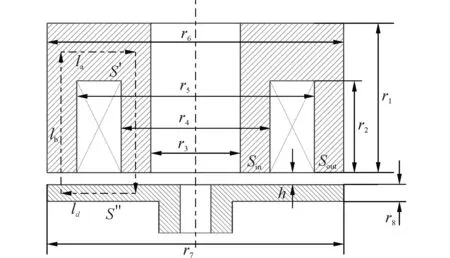
圖1 高速電磁閥結構示意圖Fig.1 The structure of high-speed solenoid valve (HSV)

根據圖2所示，高速電磁閥的總磁阻Rtotal計算公式為

Rtotal=Rgap1+Rgap2+Rarm+Riron

(2)

式中：Rgap1為主磁極對應的氣隙磁阻,Rgap2為副磁極對應的磁阻，Rarm為銜鐵的磁阻，Riron為鐵芯的磁阻。相應地，各部分的磁阻計算公式如下

(3)

式中：Sin為主磁極橫等效截面積；Sout為電磁閥副磁極等效橫截面積；h為電磁閥氣隙寬度；lb為電磁閥鐵芯內部垂直方向的磁路等效長度；la為電磁閥鐵芯內部水平方向的磁路等效長度；ld為銜鐵內部水平方向的磁路等效長度；μ為電磁閥軟磁材料磁導率，由電磁閥的B-H基本磁化曲線確定；S″為銜鐵內部對應ld的磁路等效橫截面積；S′為銜鐵內部對應la的磁路等效橫截面積。各部分磁路對應的平均磁路長度如下

(4)

最終，高速電磁閥電磁力的計算公式為

(5)

1.2 B-H基本磁化曲線擬合公式

在高速電磁閥電磁力數學模型中，軟磁材料磁導率μ一方面體現軟磁材料磁阻對電磁閥電磁轉化的影響，另一方面體現電磁閥驅動電流對磁阻的影響，上述所建立的電磁閥電磁力數學模型正是通過軟磁材料磁導率實現高速電磁閥電-磁的瞬變耦合。磁性材料的B-H基本磁化曲線決定材料的瞬變磁導率，因此，B-H曲線擬合公式的準確性直接影響電磁閥電磁數學模型的預測準確性。

Jiles等[13]提出了描述磁化現象和磁滯現象的Jiles-Atherton模型(簡稱J-A模型)，J-A模型廣泛應用在電磁電機仿真計算等領域，但是在使用J-A模型進行計算時，需要對模型中的五個關鍵系數進行確定，而這五個系數通常是采用較復雜的數學方法并基于試驗數據進行擬合確定的。Leite等[14]采用遺傳算法進行J-A模型系數的確定，并通過試驗值和仿真值的最小均方差進行校核。Monia等[15]研究了J-A模型中五個系數對磁性材料磁化過程的影響，發現五個系數中的每一個均明顯影響磁化和磁滯數學模型預測的準確度。在使用J-A模型進行磁性材料磁化過程和磁滯過程描述時，模型中五個系數的精確確定給J-A模型在工程上的應用帶來一定的困難。因此，急需尋找一種工程上應用簡單且計算精度高的軟磁材料B-H磁化曲線擬合公式，該擬合公式可正確描述磁性材料的非線性磁化特性和磁飽和現象。

Chan等[16]假設磁性材料的磁滯回線是以B-H基本磁化曲線為對稱軸分布的，由此得到計算軟磁材料基本磁化曲線的數學模型：

(5)

從圖3看出，Chan提出的公式僅能保證在初始磁化階段和磁飽和階段預測值和試驗值具有較好的吻合性，而無法正確預測從初始磁化到接近磁飽和的變化過程。

一維商業軟件AMESim[17]在進行電磁過程計算時，采用式(6)進行電磁執行器電磁轉化過程中磁性材料B-H磁化曲線的描述，式(6)中的待定系數A由式(7)確定:

(6)

(7)

式中：Ms為飽和磁化強度，Mr為剩余磁化強度，Bs為飽和磁感應強度，Hs為飽和磁化強度對應的磁場強度，Hc為矯頑力，μ0為真空磁導率。

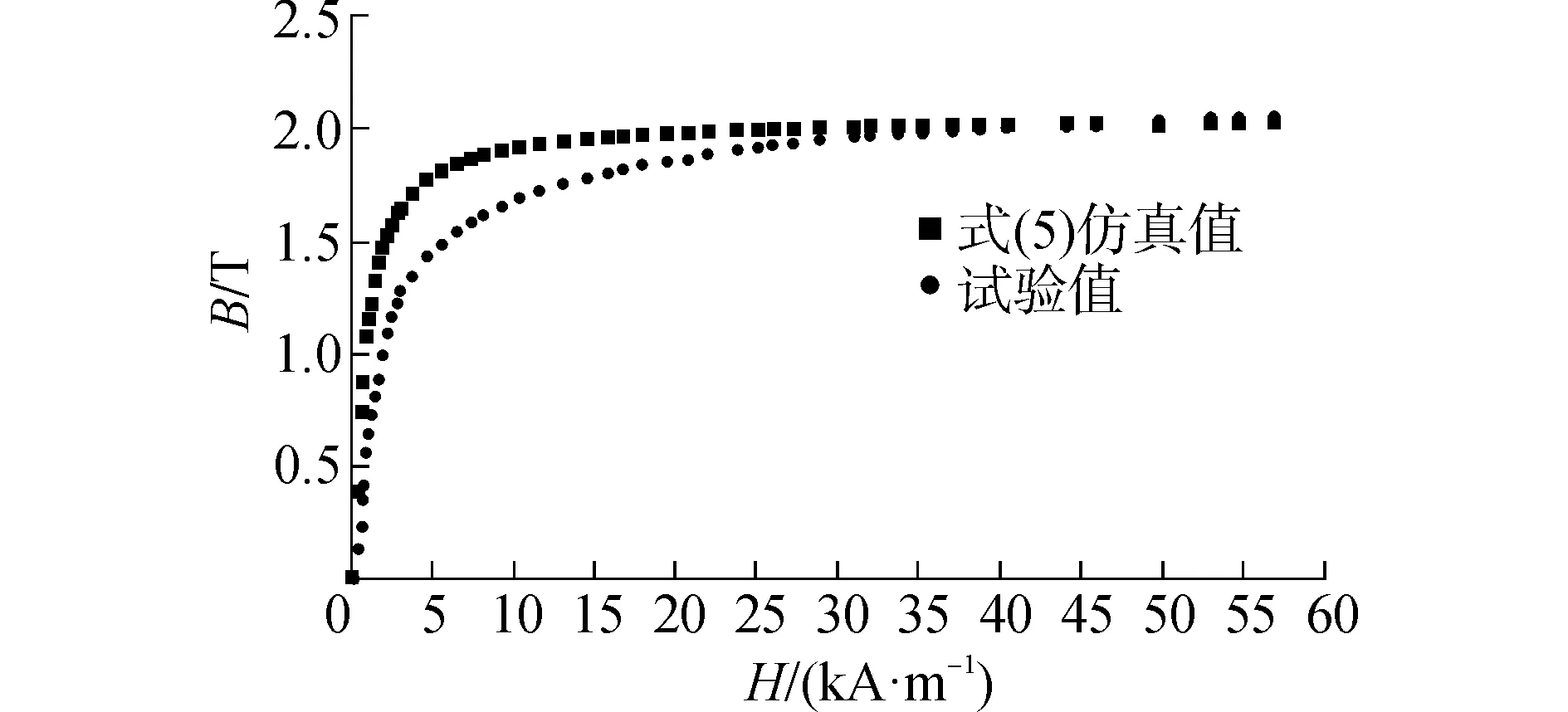
圖3 Chan公式的計算結果和B-H曲線試驗結果的對比Fig.3 Comparison between simulated by formula proposed Chan and experimental results of B-H curves

從圖4看到，當采用AMESim軟件提供的B-H曲線擬合式(6)和(7)時，預測值已經不能正確描述磁性材料真實的磁化過程。當采用式(6)時，式中的待定系數A不通過式(7)確定，而是根據試驗的B-H磁化曲線調整，那么當A=5 000時，AMESim提供的擬合公式可以比較正確的描述磁性材料的磁化過程，但同式(6)存在的問題一樣，該擬合公式仍無法準確地描述軟磁性材料從初始磁化向磁飽和的過渡階段。

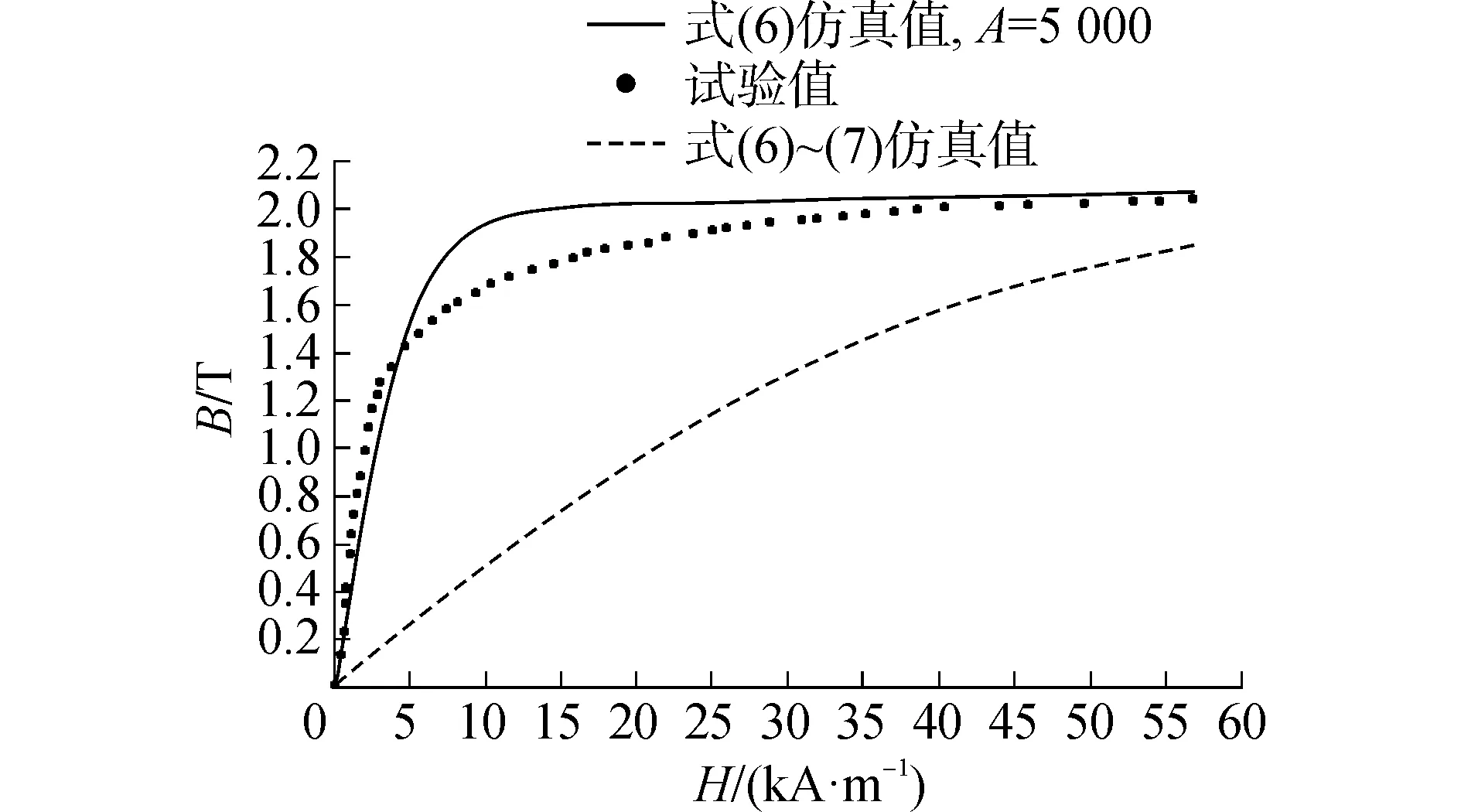
圖4 AMESim公式計算結果和B-H曲線試驗結果的對比Fig.4 Comparison between simulated by formula proposed AMESim and experimental results of B-H curves

從圖5所示的磁性材料(包括硬磁材料和軟磁材料)B-H基本磁化曲線示意圖上看到，隨H的增加，B開始會迅速增大，但當H較大后，B不會隨著H的增加而無限增大，而是逐漸接近最大磁飽和強度Bs，因此，所選擇的擬合公式也應可以正確描述圖5中所示的B隨H的變化規律。

在眾多的函數形式中，對數函數log(x)所反映的曲線變化規律接近于圖5所示B-H基本磁化曲線的變化規律。選擇對數函數的另一個重要的原因是，對數函數形式可以保證即使當H無限大時，隨H的增加，B仍可以保持很小程度的增加，因為只有在H的整個變化區間內B一直在增大，磁導率μ(μ=ΔB/ΔH)才能保證不為零，這樣式(5)、(6)才具有物理意義。此外，為減少B-H曲線擬合公式中系數的數量，確定以e為底的自然對數ln(x)的形式作為B-H曲線擬合公式的基本形式。對于每一種磁性材料，其基本磁化曲線均是從原點開始，即當H=0時B一定為零，而ln(x)對數是不存x=0點，因此把ln(x)對數轉化成ln(x+1)的形式，這保證了ln(x+1)的擬合公式滿足磁性材料B-H磁化曲線通過原點(0,0)的物理意義，綜合上述因素，確定了B-H曲線擬合公式的基本形式為

B=ln(H+1)

(8)

圖5 B-H磁化曲線示意圖Fig.5 Diagram of B-H magnetization curve

每一種磁性材料具有不同的磁飽和強度Bs和最大磁導率μmax，Bs值決定磁性材料磁飽和特性，μmax決定磁化曲線的非線性磁化過程，為了實現B-H曲線擬合公式適用于任意的磁性材料的磁化曲線的擬合，需要在擬合公式中引入兩個系數p1和p2，利用系數p1調節擬合曲線所能達到的磁飽和強度Bs，利用系數p2調節磁化曲線從初始磁化向臨界磁飽和的轉化過程。式(9)為在式(8)基礎上引入系數p1的擬合公式。從圖6可以看到，隨著系數p1的增加，擬合曲線的最大磁感應強度逐漸增大，特別是當p1=0.2時，式(9)得到的擬合曲線在描述磁飽和強度方面和試驗數據有著較好的吻合性，同時注意到，無論系數p1取值多少，在初始磁化階段，計算值和試驗數據均存在著較大誤差，已無法準確描述磁性材料在初始磁化階段的非線性磁化過程。

B=p1ln(H+1)

(9)

式(10)為在式(8)基礎上引入系數p2的B-H曲線擬合公式。從圖7可以看到，隨著系數p2的增加，在初始磁化階段，擬合曲線和試驗數據的吻合性越來越好，特別是當p2=0.000 9時，式(10)比較準確的描述了磁性材料的初始磁化過程，但注意到，由于沒有在擬合曲線中引入系數p1來限制最大磁感應強度，所以看到式(10)計算的最大磁感應強度隨系數p2的增加而增大。

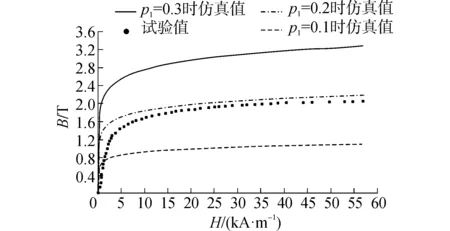
圖6 系數p1對B-H擬合曲線的影響Fig.6 Influence of p1 on B-H fitting curves

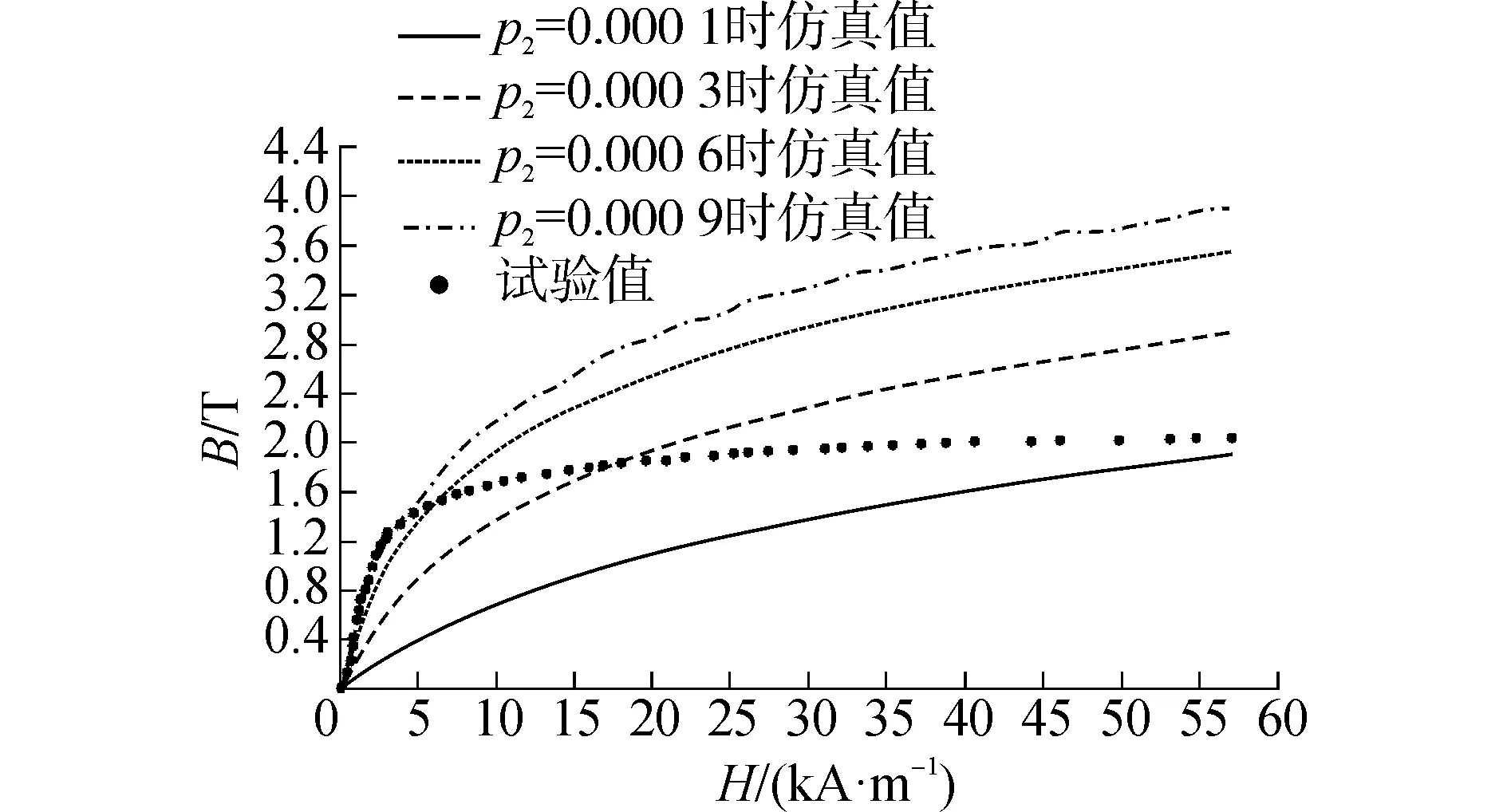
圖7 系數p2對B-H擬合曲線的影響Fig.7 Influence of p2 on B-H fitting curves

(10)

從上面的分析可以看出，在擬合公式中需要引入系數p1和p2，以實現擬合公式對任何軟磁材料具有普遍的適用性。式(11)為綜合引入p1、p2系數后的B-H曲線擬合公式，式中系數p1和p2可通過在試驗B-H基本磁化曲線上選擇的兩個數據點(H1,B1)和(H2,B2)來確定，點(H1,B1)推薦選在Bs/2處，如圖5所示，而點(H2,B2)推薦選在接近Bs處：

B=p1ln(p2H+1)

(11)

從圖8看到，擬合公式(11)給出的計算值和試驗B-H曲線相差極大，分析產生這種現象的原因是p1和p2兩個系數的同時引入會成倍增大擬合公式計算得到的最大磁感應強度。通過對式(11)分析發現，p1的引入會驟然增大擬合公式的斜率，然而缺少p1又會導致擬合公式無法實現描述磁飽和的現象的，因此，在式(11)的基礎上，經過大量的計算分析確定：

(12)

從圖9所示的對比結果看到，式(12)所示的B-H曲線擬合公式預測的結果和試驗值在整個磁化過程中具有非常好的吻合性，計算值和試驗值最大誤差不超過5%，該擬合公式不僅可以描述磁性材料的磁飽和現象(即磁飽強度)，而且還可以描述磁性材料的非線性磁化過程(從初始磁化向臨界磁飽和發展)。

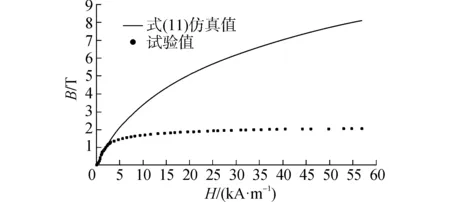
圖8 式(11)計算值和試驗數據的對比Fig.8 Comparison between simulated by (11) and experimental results of B-H curves

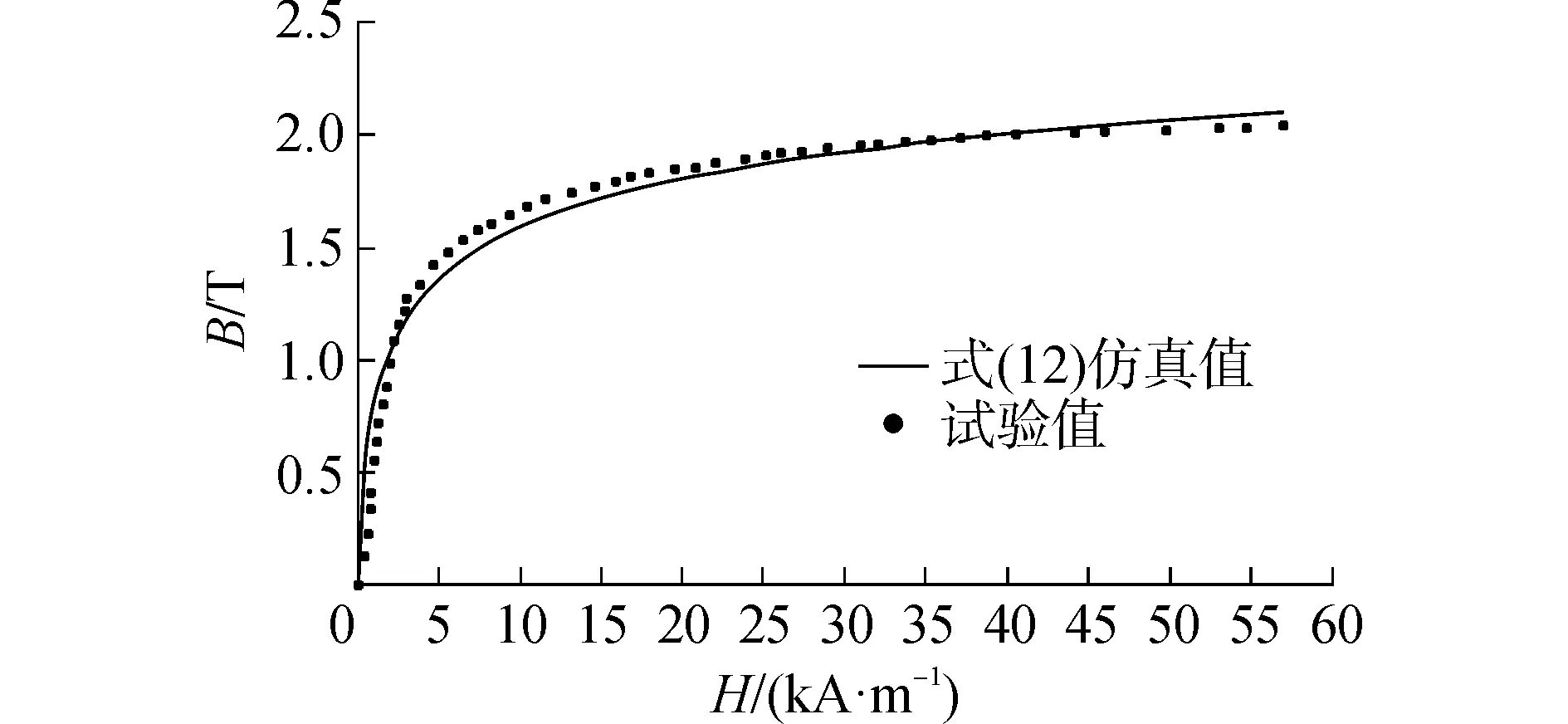
圖9 式(12)計算值和試驗數據的對比Fig.9 Comparison between simulated by (12) and experimental results of B-H curves

2 高速電磁閥靜態電磁力數學模型驗證

為驗證所建立的高速電磁閥靜態電磁力數學模型的正確性，采用圖10所示的電磁閥靜態電磁力試驗裝置進行不同驅動電流下電磁閥靜態電磁力的試驗驗證。表1給出了該電磁閥靜態電磁力試驗裝置主要儀器的測量精度。

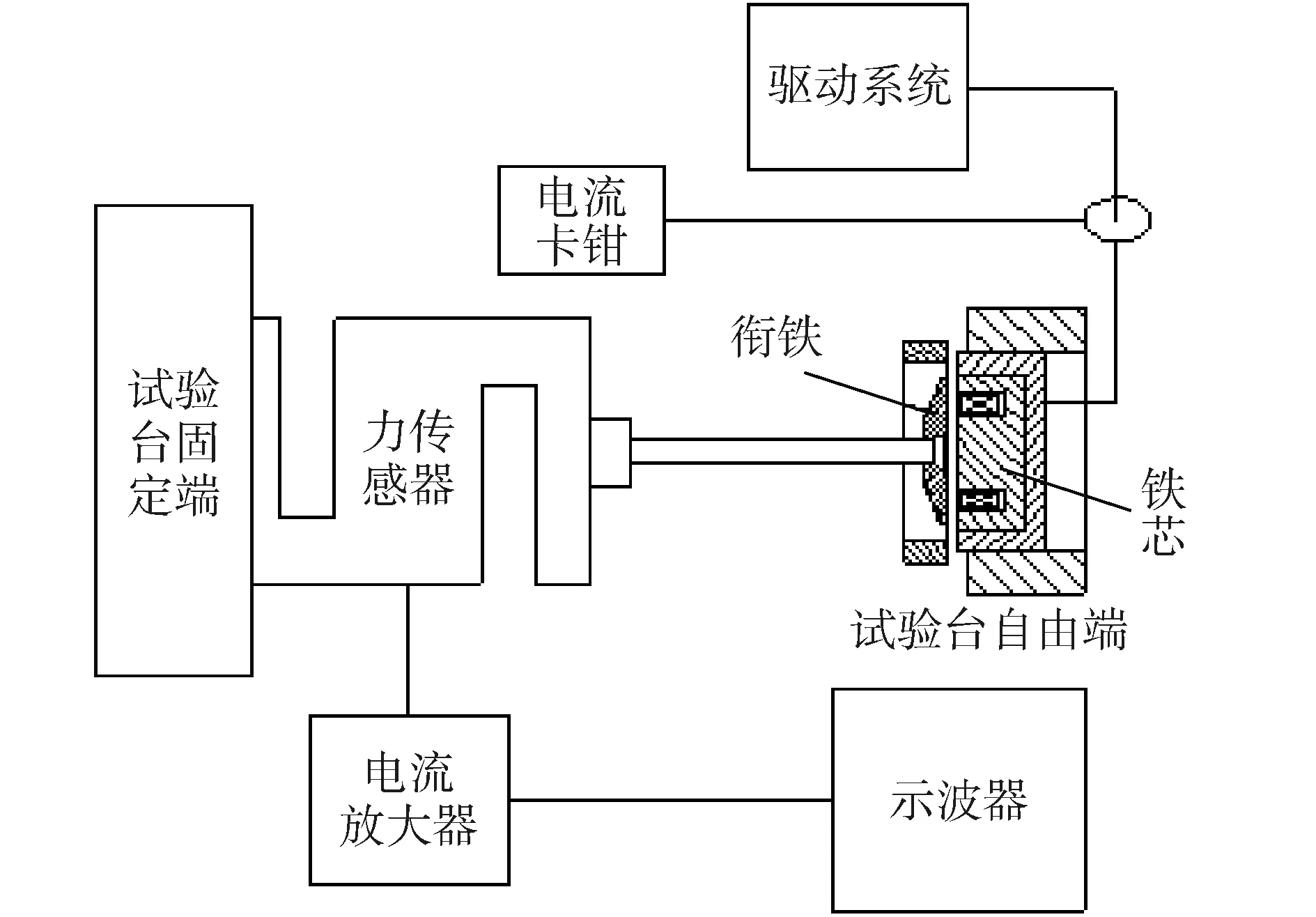
圖10 高速電磁閥靜態電磁力試驗臺示意圖Fig.10 The block diagram of test bench for HSV

儀器產品類型測量范圍測量精度/%力傳感器CZLYB-3ChengduXingputransducerCo.,Ltd.0～500N≤0.05電流探針1146AAgilenttechnology1～100A≤±2

表2所示為所研究的高速電磁閥的詳細結構參數。0.10 mm和0.12 mm的氣隙是目前MAN公司和WARTSILA公司船用共軌噴油器高速電磁閥的氣隙寬度，因此選用上述兩種氣隙下的電磁力試驗數據進行上述電磁閥靜態電磁力數學模型的驗證。從圖11和12看到，在兩種工作氣隙下，在驅動電流1～18 A范圍內，高速電磁閥靜態電磁力數學模型計算結果和試驗數據具有非常好的一致性，證明了所建立數學模型預測結果的準確性。

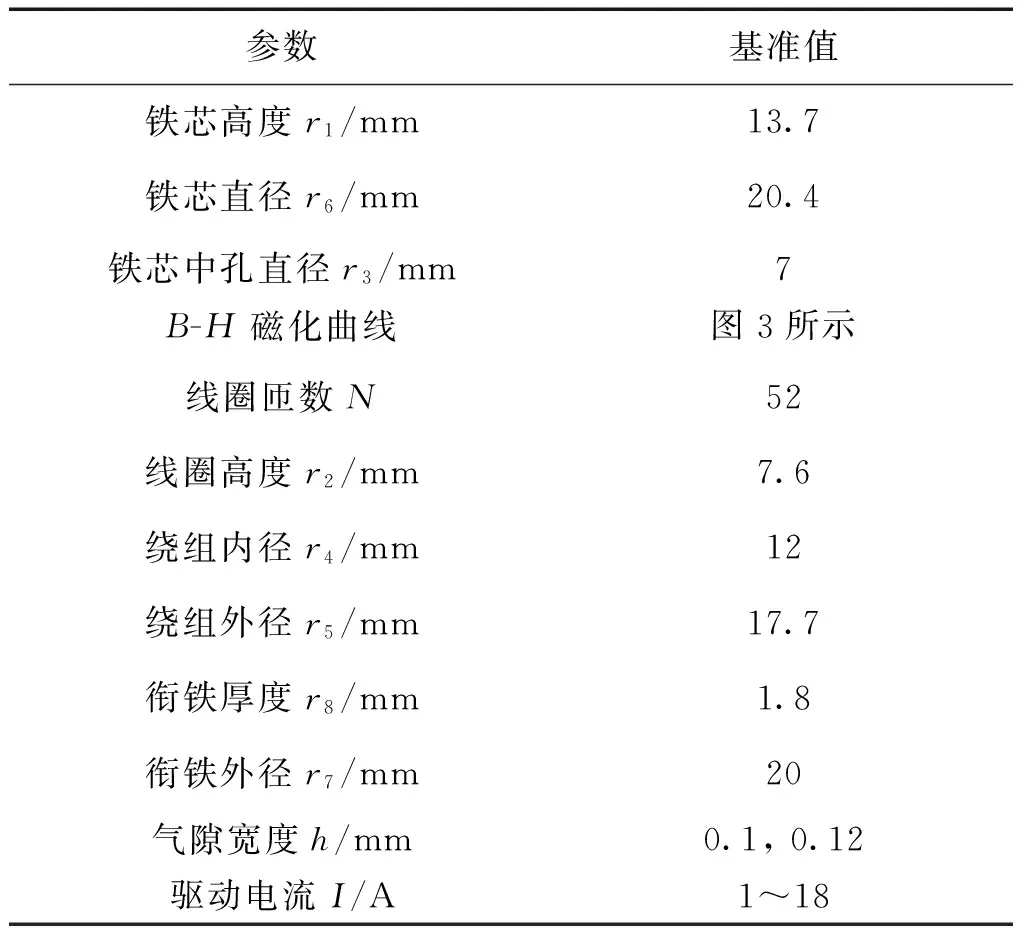
表2 高速電磁閥結構參數

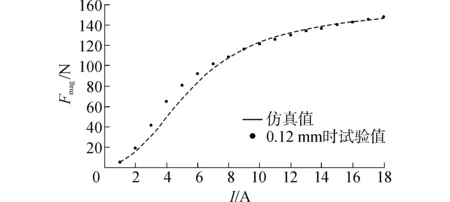
圖11 氣隙0.10 mm下電磁力計算值和試驗結果對比Fig.11 Comparison between simulated and experimental results of electromagnetic force in 0.1 mm of air gap width

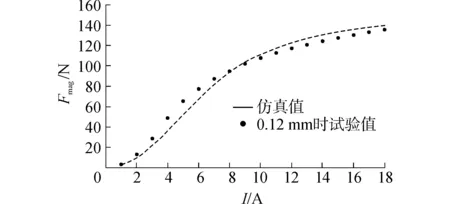
圖12 氣隙0.12 mm下電磁力計算值和試驗結果對比Fig.12 Comparison between simulated and experimental results of electromagnetic force in 0.12 mm of air gap width

3 結論

1)提出了具有普適性的B-H曲線擬合公式，計算值和試驗值的對比表明了所提出的磁化曲線擬合公式可正確描述軟磁材料的非線性磁化過程和磁飽和現象。

2)在高速電磁閥靜態電磁力數學模型中，通過磁性材料磁導率把磁性材料對電磁轉化影響的因素引入到電磁閥數學模型中，基于電磁耦合原理，建立了考慮最大電磁力飽和的高速電磁閥靜態電磁力數學模型，利用試驗數據驗證了該模型的正確性。

3)基于上述建立的高速電磁閥靜態電磁力數學模型，可開展結構參數對電磁閥電磁力的優化研究，為后期高速電磁閥的設計提供技術支撐。

[1] LIU P, FAN LY, HAYAT Q, et al. Research on key factor and theirs interaction effects of electromagnetic force of high speed solenoid valve[J]. The scientific world journal, 2014, 5: 1-13, ID567242.

[2] SUN Z Y, LI G X, WANG L, et al. Effects of structure parameters on the static electromagnetic characteristics of solenoid valve for an electronic unit pump[J]. Energy convers manage, 2016, 113(1): 119-130.

[3] CHENG Q, ZHANG ZD, GUO H, et al. Improved processing and performance of GDI injector based on metal injection molding technology[J]. International journal of applied electromagnetics and mechanics, 2014, 44(1): 99-114.

[4] MILLER J I, FlACK T J, CEBON D. Modeling the magnetic performance of a fast pneumatic brake actuator[J]. Journal of dynamic systems measurement and control-transactions of the ASME, 2014, 136(2): 729-736.

[5] SALVADOR F J, MARTI-ALDARAVI P, CARRERES M, et al. An investigation on the dynamic behavior at different

temperatures of a solenoid operated common rail ballistic injector by means of a one dimensional model[C]//SAE Paper. Detroit, Michigan, 2014: 2014-01-1089.

[6] SALVADOR F J, GIMENO J, DE LA MORENA J, et al. Using one-dimensional modeling to analyze the influence of the use of biodiesel on the dynamic behavior of solenoid-operated injector in common rail systems: results of the simulations and discussion[J]. Energy convers manage 2012， 54: 122-132.

[7] PAYRI R, SALVADOR F J, MARTF-ALDARAVF P, et al. Using one-dimensional modeling to analyze the influence of the use of biodiesel on the dynamic behavior of solenoid-operated injector in common rail systems: detailed injection system model[J]. Energy convers manage 2012， 54: 90-99.

[8] BENEDIKT H, HEINZ U. Modeling and experimental validation of the solenoid valve of a common rail diesel injector[C]//SAE Paper. Detroit, Michigan, 2014: 2014-01-0195.

[9] TOPCU E E, YUKSE I, KAMIS Z. Development of electro-pneumatic fast switching valve and investigation of its characteristic[J]. Mechatronics, 2006, 16(6)： 365-378.

[10] JIN Y Z, DENG R Y, JIN Y Z, et al. Research on the response characteristics of solenoid valve of the air-jet loom by simulation[J]. International journal of thermal sciences, 2013, 22(6)： 606-612.

[11] MEHMOOD A, LAGHROUCHE S, BAGDOURI M E. Nonlinear dynamic modeling of an electro-pneumatic pressure converter for VGT pneumatic actuator[J]. International journal of automotive technology, 2013, 14(6): 941-953.

[12] SEFKAT G. The design optimization of the electromechanical actuator[J]. Struct Mul Tidiscip O, 2009, 37(37): 635-644.

[13] JILES D C, ATHERTON D L. Theory of ferromagnetic hysteresis[J]. Journal of magnetism and magnetic materials, 1986, 61: 48-60.

[14] LEITE JV, AVILA S L, BATISTELA N J, et al. Real coded genetic algorithm for Jiles-Atherton model parameters identification[J]. IEEE transactions on magetics, 2004, 40(2): 888-891.

[15] MONIA F J. Magnetic hysteresis modeling and numerical simulation for ferromagnetic materials[C]//52ndConference on Decision and Control. Florence, Italy, 2013: 516-523.

[16] CHAN J H, VLADIMIRESCU A, GAO X C, et al. Nonlinear transformer model for circuit simulation[J]. IEEE T Comput Aid D, 1991, 10(4): 476-482.

[17] LMS Imagine. User′s Guide of AMESim Rev12[EB/OL]. Germany: LMS. (2013). AMESim Rev12 Help.

本文引用格式：

趙建輝， 格列霍夫·雷奧尼德， 范立云， 等. 高速電磁閥靜態電磁力數學模型[J]. 哈爾濱工程大學學報， 2017， 38(12): 1884-1889.

ZHAO Jianhui, GREKHOV Leonid, Fan Liyun, et al. Investigation of high speed static electromagnetic force model of solenoid valve[J]. Journal of Harbin Engineering University， 2017， 38(12): 1884-1889.