基于Matlab的鐵附件虛擬包裝優化設計
錢哨,申進,胡舉綱,李亮,仇愛軍,卞振華,季明星
(1.國網江蘇省電力有限公司鹽城分公司,鹽城 224051;2.鹽城工學院,鹽城 224051)
引言
鐵附件是電力線路輸變電用構(附)件的俗稱,是根據用戶的特殊要求而進行生產的非標準件產品,范圍覆蓋10kV及35kV、110kV、220kV輸電線路及變電站用構件,以及交通和市政用到的一些非標件。由于其形狀不規整,占地面積較大,所以對鐵附件倉儲帶來很大的困擾。
主要存在問題如下:(1)同種型號不同廠方尺寸規格的不一致;(2)結構不規整導致擺放倉儲凌亂;(3)進出庫計數和發放困難;(4)占地面積大不符合倉儲5S標準。如何有效的解決各類鐵附件產品的倉儲就涉及到其規格尺寸標準化、包裝標準化和倉儲標準化的問題。
本文根據目前鐵附件包裝存在的問題,結合包裝容器結構設計的主要特點,利用Matlab編程軟件對典型鐵附件零件進行了包裝結構優化設計,并且結合NX軟件實現鐵附件包裝的虛擬裝配和分析。
1 鐵附件零件特點分析
常見的鐵附件零件種類包括了扁鐵成套抱箍、扁鐵洋元抱箍、電纜抱箍、連接鐵、橫擔、頂套等多種規格多種型號。其尺寸系列和形狀結構各不相同。僅扁鐵洋元抱箍又分為直徑100到直徑400等40種不同尺寸規格。目前鐵附件零件倉儲面臨的最大問題就是安放的雜亂無章,沒有一種統一的包裝設計。并且對于零件的清點計數、發放等都帶來了很大的問題。設計一種內部結構可調整,外部結構尺寸統一的包裝箱是目前鐵附件零件倉儲急需解決的問題。
2 結構優化設計分析
根據鐵附件零件的結構特性,并且結合設計需求,最終的包裝箱必須能夠安放在貨架之上,并且每個包裝箱承載的重量受到貨架規格的限制。本文利用MATLAB仿真軟件,將所需設計的包裝箱尺寸、重量作為設計變量,通過軟件編程求優化向量,使設計目標函數取得極值。
3 基于Matlab的優化設計
Matlab軟件是一款非常優秀的數值計算和圖形圖像處理工具軟件,其優化工具箱含有一系列優化算法函數,這些函數拓展了Matlab數字計算環境的處理能力,可以解決復雜結構的優化問題[2]。
根據鐵附件結構的特點,其包裝箱的優化設計是有約束的非線性規劃問題。利用Matlab函數fmincon( )處理有約束的非線性多元變量的優化問題[3],該命令的具體格式為:[x, fval, exitflag,output, lambda, grad, hessian] = fmincon (fun,x0, A, b, Aeq, beq, lb, ub, nonlcon, options)。
說明:
(1)參數中fun是目標函數,x0為初始值,x為返回的設計變量值。
(2)A和b表示線性不等式約束,A為系數矩陣,b為向量;Aeq和beq表示線性等式條件,Aeq為系數矩陣,beq為向量;lb和ub分別為優化參數x的上下界;nonlcon表示非線性約束條件;options為設置優化選項參數[3]。
(3)返回值fval為目標函數在最優解X點的函數值;exitflag為返回算法的終止標志,exitflag>0表示優化結果收斂于解,exitflag<0表示優化結果不收斂于解,exitflag=0表示優化超過了聲明的代入函數值的次數;output為返回優化算法信息的一個數據結構;lambda是拉格朗日乘子,顯示是哪個約束條件有效;grad和hessian分別表示最優解x點的梯度和Hessian矩陣值[4]。
4 優化設計實例
針對典型鐵附件零件洋元進行結構優化設計(圖1、圖2所示),直徑為D=200mm,長L=270mm。設計一種滿足盛裝體積在1m3的包裝結構。并且要求能夠實現洋元的固定,包裝箱總重量小于1.5噸,能夠通過叉車安放在貨架之上。

圖1 直徑D=200洋元
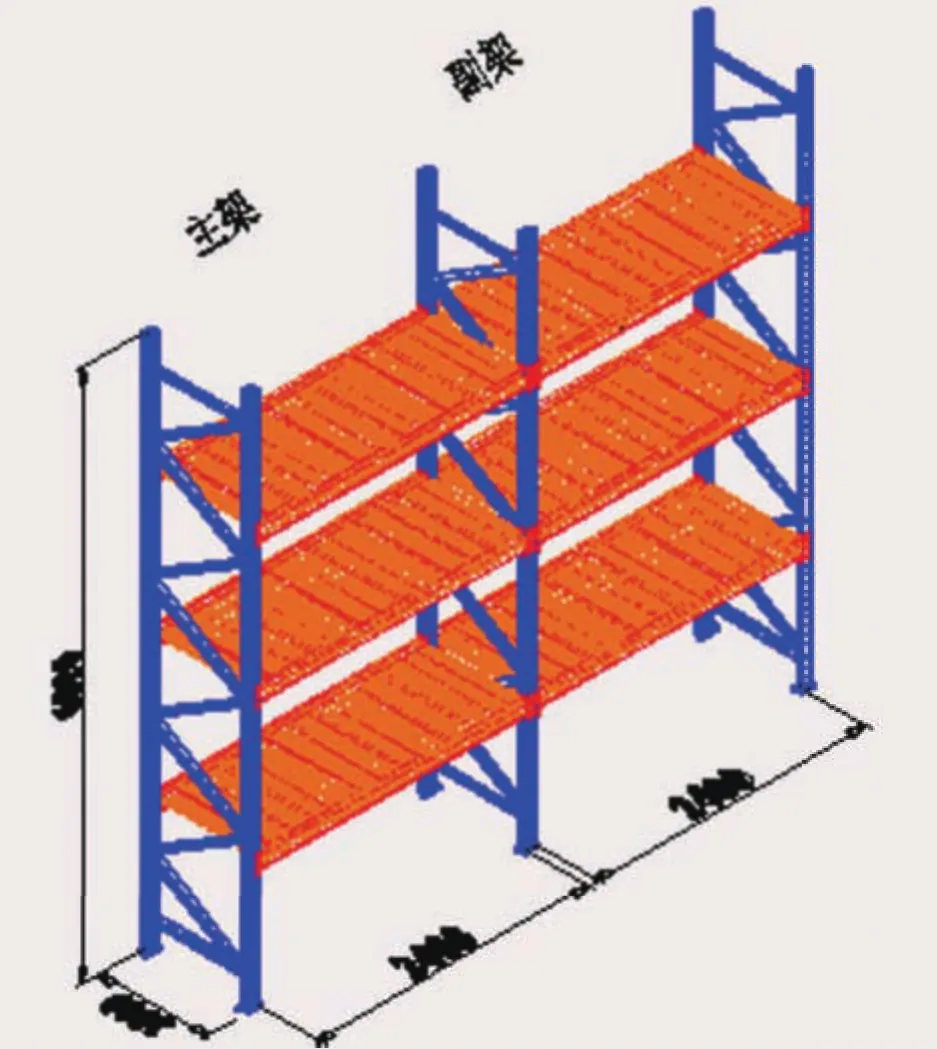
圖2 貨架規格
根據其設計要求,其外形尺寸必須滿足國家電網規定的貨架安放規格,即長X,寬Y,高Z之和必須小于3.2m。試求該包裝結構用料最省,安放最合理的結構參數X,Y,Z。該問題的設計目標是使包裝箱在滿足包裝要求情況下用料最省,而包裝箱材料的多少是與箱坯的面積大小直接相關的。若不計粘結邊的面積,則問題可以轉化為在約束條件:X*Y*Z=1;X+Y+Z≤3.2;X>0,Y>0,Z>0。選用Matlab9.0軟件來進行上述目標的設計,具體的步驟如下:
(1)首先利用 Matlab9.0的程序編輯器建立目標函數的objfun.m
function f=objfun(x)
f=2*[X+Y]*[X+Z];
(2)然后再建立約束條件的m文件confun.m
function [c, ceq] = confun (x)
c = [];
(3)輸入優化命令
> > x0= [1 1 1];
> > A = [1,1,1];
> > b = [1. 6]
> > lb = [0; 0; 0];
> > options = optimset ('LargeScale', 'off','Display', 'iter');
我說“:隨您怎么說,說心中想說的就可以。”婆婆清了清嗓子,微笑著說:“我兒媳曾經告訴我,是一家人,就要說家人該說的話,做家人該做的事,正是堅持這一點,我們婆媳從矛盾重重走到今天的相親相愛。”
> > [x, fval, exitflag, output] = fmincon('objfun', x0, A, b, [], [], lb, [], 'confun', options)
完成以上步驟以后,會得到最優化的結果值:
Optimization terminated successfully:
Search direction less than 2* options. TolX and
maximum constraint violation is less than options. TolCon
Active Constraints:
1
X=1.45
Y=1.4
Z=0.97
fval=1.5390
exitflag=1
output=
iterations: 13
funcCount: 73
stepsize: 1
algorithm: [1x44 char]
firstorderopt: 1. 3270e - 004
cgiterations:[]
根據以上優化設計方法與程序運行結果發現,當包裝箱的結構參數X=1.45m,Y=1.4m,Z=0.97m時,此時尺寸比例滿足理想尺寸的比例條件2:1:2,而且材料用量fval為最小值;同時,終止迭代的錯誤條件exitflag=1>0,表示優化結果收斂于解,優化是成功的。
5 仿真設計和虛擬裝配
通過上述的Matlab結構優化仿真我們可以對洋元結構包裝箱的外部尺寸進行最優化的設計。解決了外部尺寸設計的問題,我們可以通過NX軟件對包裝箱內部結構進行仿真設計和虛擬裝配(圖3為D200洋元虛擬裝配效果圖)。
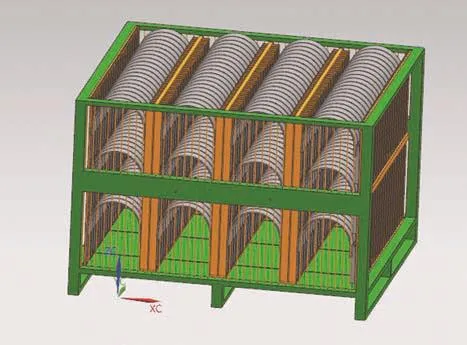
圖3 D200洋元虛擬裝配效果圖
通過對洋元結構特點的分析,本文采用插槽式安裝方法,設計的特點如下:(1)插槽式安裝便于實現洋元結構的兩側固定,不會在運輸和存儲過程中出現掉落現象;(2)3層結構設計,最大程度上利用了箱體空間,實現包裝零件數量最大化;(3)固定插槽數目設計,便于清點、發放、計數。同時通過虛擬設計可以對不同種尺寸洋元進行數量統計(表1所示)。
6 結語
根據包裝容器結構尺寸優化設計的特點,分析了計算機輔助優化設計的一般流程和求解方法,選用Matlab 軟件實現了設計目標。優化設計結果不僅美化了包裝件的外觀,而且降低了包裝成本;同時,利用三維設計軟件進行虛擬設計,既減少了設計者的工作量,又加快了設計速度。
[1]飛思科技產品研發中心. MATLAB6.5輔助優化計算與設計[M].北京:電子工業出版社,2003.
[2]王德忠.包裝計算機輔助設計[M].北京:印刷工業出版社, 1999.
[3]石博強,滕貴法,等. MATLAB數學計算范例教程[M].北京:中國鐵道出版社,2004.
[4]廖敏,戴躍洪.瓦楞紙箱結構設計及其優化方法[J].包裝工程,2006,27(4): 153-156.
[5]甘純剛,等.瓦楞紙箱結構優化的CAD系統[J].包裝工程,2006,27(5): 155-158.
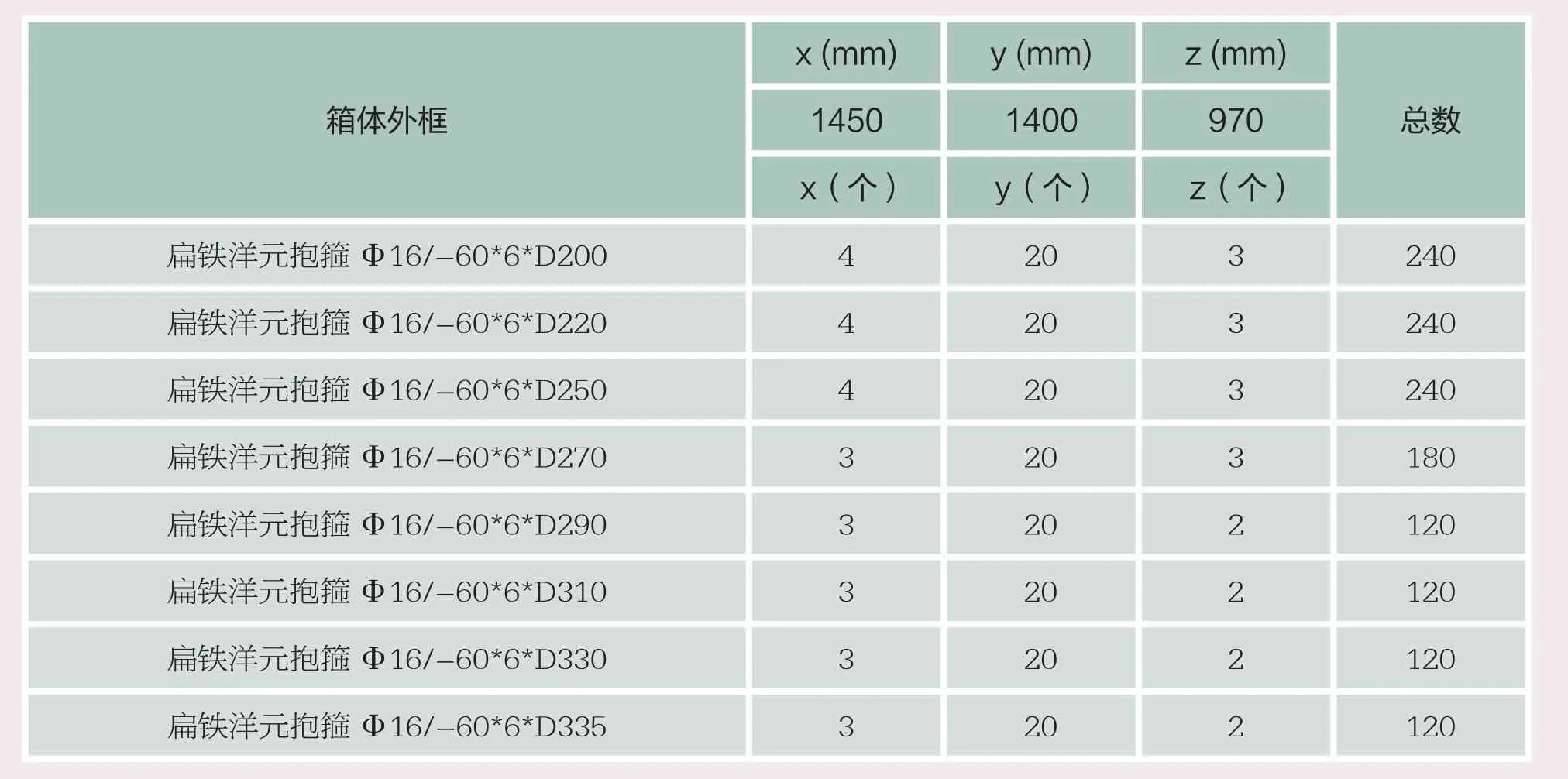
表1 包裝箱尺寸和各型號安裝數量

