水電站和電力調度量測系統的狀態估計探析

劉小龍，劉 俊

（1.陜西省漢中市石門水庫管理局，陜西 漢中 723000；2.中國電力科學研究院，江蘇 南京 210003）

0 引言

水電站和電力調度系統量測數據在采集、傳遞、交換過程中不可避免存在誤差，包括個別可預測的偶然誤差和帶有部分規律性的系統誤差。此外還包括偏離實際量測數據變化軌跡較遠的數據，即粗差。粗差的出現約占量測系統量測總數的1%~10%[1]。

隨著新理論在電力系統中的應用，多種抵御粗差能力的狀態估計新方法應運而生。如新息圖狀態估計[2]、最小信息損失狀態估計[3]等，這些方法分別從不同思路獲取有利于估計的信息，提高了狀態估計抵御粗差的能力。

本文提出了一種基于線性分段權函數的選權迭代狀態估計方法，并在調度仿真平臺上驗證，該方法通過選取“三段式”線性權因子函數，根據量測殘差確定不同設備類型量測點等價權值，將傳統加權最小二乘狀態估計方法[4]和抗差估計理論相互結合，既保留加權最小二乘估計計算的高效快速性，又使得狀態估計算法本身具備較強抵御粗差的能力。

1 傳統粗差檢測和定位

狀態估計傳統的粗差檢測和定位一般采用估計-粗差檢測與辨識-再估計-再粗差檢測與辨識的兩輪迭代計算模式，即估計后辨識的方法。對于較大偏差的量測粗差數據可以將其識別出來，但對于偏離真值較小的量測數據，則無法通過粗差檢測和定位完全將其影響消除，導致這些不正確的數據參與了狀態估計，從而對正確數據形成污染，造成誤檢和漏檢。

針對上述問題，本文提出了基于線性分段權函數的選權迭代狀態估計方法，對于超過辨識門檻的量測數據但仍可用于計算的量測量，即對估計精度提高有貢獻的量測量，不采用刪除和抑制的策略，而采取降權方法降低該量測的權重，使該量測通過降權方法仍參與狀態估計計算，為狀態估計精度提高作出貢獻。而對于殘差很大的不良數據，權值強制為零，使其不影響狀態估計計算精度。

2 選權迭代狀態估計方法

選權迭代狀態估計方法是在粗差不可避免的情況下，選擇適當的算法使電網狀態量估計盡可能減免粗差的影響，得出正常模式下的最佳估值。其原則是充分利用有效量測，限制利用可使用量測，排除有害量測。

權函數是衡量選權迭代狀態估計方法優劣的一個重要因素，經典選權迭代狀態估計的權函數都是以降權思路提出的，通過不斷迭代，使含粗差項量測值的權趨近少零，本文也是基于上述思想，通過建立分段線性的權因子函數，得到既有較強抵御粗差能力，又有較高效率的估值。

2.1 問題求解

選權迭代狀態估計通過等價權函數將抗差估計理論與最小二乘形式相互結合，其權是殘差的函數，計算迭代式為：

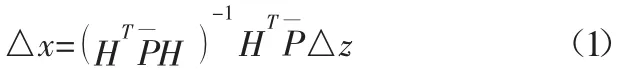
本文所述求解方法與傳統的最小二乘算法的區別是：本文方法在估計迭代計算中量測權值隨量測殘差變化，其權值按照三段式線性權函數確定。而最小二乘算法在求解過程中權值保持不變；本文方法對可利用量測采取線性函數降權處理模式，而傳統狀態估計粗差檢測和定位方法中對量測采用“非此即彼”一刀切處理模式。

2.2“三段式”權函數

選權迭代狀態估計根據量測殘差所處區域，將權區域劃分為保權區、降權區、淘汰區。從而充分利用有效信息，限制性利用可用信息，排除有害信息，因此將這種估計方法使用的權函數稱為“三段式”權函數，其函數曲線如圖1所示。

圖1“三段式”權函數

圖1中a、b、c均大于零，其值，其中a為保權區邊界系數，b為降權斜率控制系數，c為淘汰區邊界系數，為量測誤差的標準差，它決定于量測、變換與傳送各個環節誤差的總和，其值由缺省量測權值確定，r為測點量測殘差，w（r）為測點權因子。

根據測量誤差理論，邊界系數a可取2.5，這個區間以外的量測值既必能完全排除又要限制其有害影響。當殘差超出±10σ時，在量測值分布模式可用的情況下，這部分數據不應作為有用的量測信息，即取權值為0。本文算例中a取2.5，b取11.5，c取10.6。

由圖1可知，當殘差r絕對值在aσ以內時，權因子w取1，即為其保權區；當殘差 r絕對值處于[aσ，cσ]區間時，權因子取為線性函數形式，權因子w逐漸減小，降低量測值在計算中的權重，量測數據偏差較大時，對其分配的權值也就越低。而當殘差r絕對值處于（cσ，+∞）區間時，這些數據不應作為量測信息，即取w等于0，為淘汰區。從函數的正半軸看過去，函數分三段，分別對應著量測數據的有用數據，有效數據以及有害信息。即相應的保權區、降權區、淘汰區，其權因子分別為：

當-aσ≤r≤aσ 時，保權區權因子

當 aσ＜r≤cσ 時，降權區權因子函數

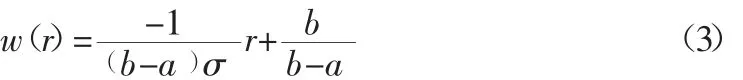
當-cσ≤r＜-aσ 時，降權區權因子函數

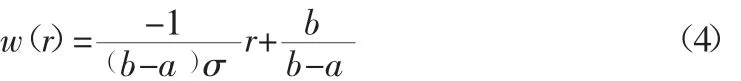
當 r＞cσ 或 r＜-cσ 時，淘汰區權因子

2.3 量測等價權

通過“三段式”權函數計算量測權因子，量測等價權為：

當-aσ≤r≤aσ 時，保權區量測等價權Pˉ為

當 aσ＜r≤cσ 或-cσ≤r＜-aσ 時，降權區量測等價權為

當 r＞cσ 或 r＜-aσ 時，淘汰區量測等價權為

式(6)和式(7)中，w'為量測點的初始缺省權值。根據各量測殘差求出對應的權因子后，通過式（6）~式（8）計算量測等價權，利用該等價權通過加權最小二乘迭代方法進行求解。

3 計算流程

基于線性分段權函數的選權迭代狀態估計在實現上采用傳統PQ解耦最小二乘估計的求解迭代方法，相比加權最小二乘法方法不同在于其量測權值隨量測殘差而變化。其殘差是指在每次迭代終了時量測量與該次迭代結果所得的量測估計量之差，殘差絕對值大的量測的權值會被減小，從而在下一次迭代中的影響也隨之減小，如此迭代下去直到收斂為止。因此，僅需對傳統加權最小二乘估計軟件作很少的修改就能達到自抵御粗差的能力，相應的計算流程如圖2所示。計算主要步驟如下：

步驟1：置迭代計數器為1，采用平啟動方式計算有功支路和注入潮流、有功殘差，進行第一次有功迭代，判斷有功最大偏差是否小于設定門檻，設置選權迭代標志。

步驟2：根據式(2)～式(5)計算測點等價權因子，在此基礎上計算量測等價權值，重新形成有功量測雅克比矩陣以及有功因子表分解。

步驟3：根據有功最大偏差量判斷有功是否收斂，否則進行無功迭代，其過程與有功迭代相似，當有功、無功偏差均小于收斂精度時狀態估計迭代計算完成。

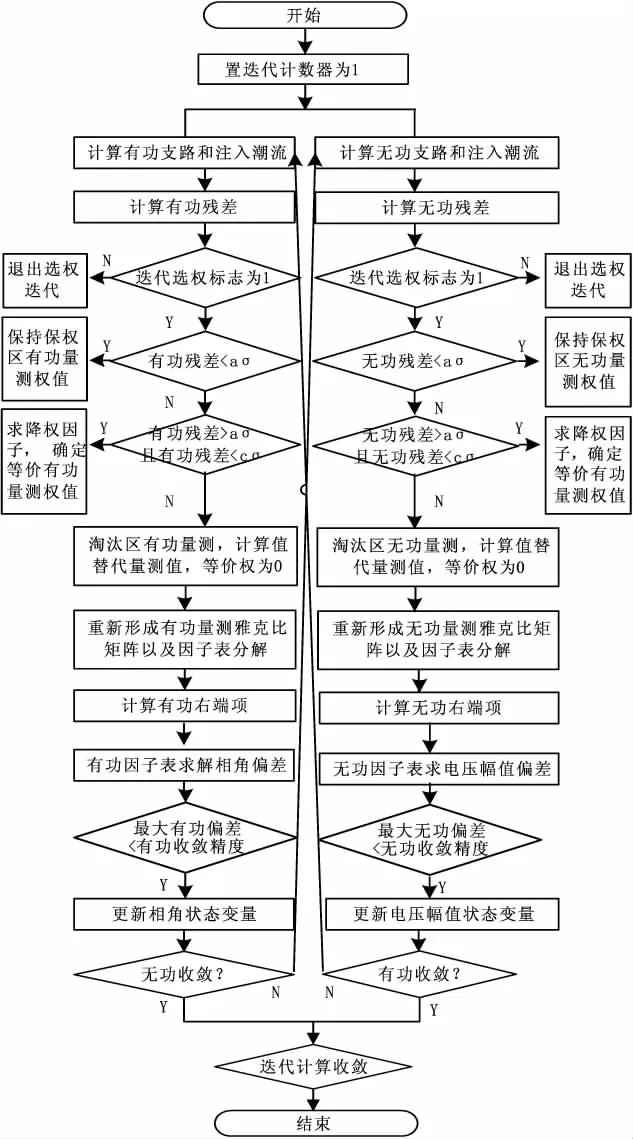
圖2 選權迭代狀態估計計算流程

4 算例分析

為驗證基于分段線性權函數的選權迭代狀態估計的計算性能，本文在智能電網調度試驗驗證平臺上選用某地調實際數據進行實驗驗證。其建模廠站數397個，建模線路總數1317個，建模變壓器總數733個，建模機組95臺，建模負荷總數6497個。電網計算母線數為1558條，量測總數為8771個。

本文將從粗差檢測和定位門檻對狀態估計計算精度影響和算法抵御粗差性能指標兩個方面對所提算法進行驗證。

4.1 狀態估計結果指標

狀態估計精度反映狀態估計結果與其真值之間的靠近程度。對基于標準節點的系統，由于標準節點的電力系統狀態真值（取潮流值）是已知的，這時選擇狀態估計結果和狀態真值之間的偏差作為估計精度的量化指標。但實際電力系統的狀態量真值是未知的，量測的估計誤差也不可知，因此不能再采用基于真值的量化指標，本文所定義的狀態估計性能指標如下：

1）狀態估計精度指標G(s)

G(s)指標如式（9）所示。其中 s為門檻值；Dot|r|＜s為量測估計殘差絕對值小于門檻值s的量測點數；Dottotal為量測總點數。

2）狀態估計有功目標函數值T11

T11指標如式（10）所示。其中zip為有功量測值；wip為有功量測權重；rip為有功量測殘差。

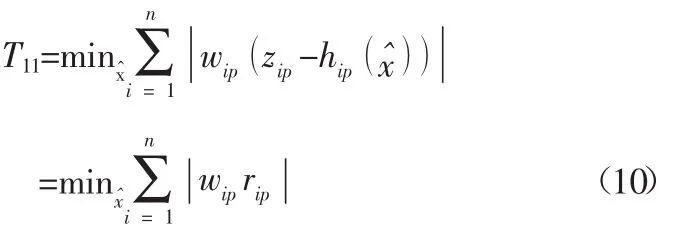
3）狀態估計無功目標函數值T12

T12指標如式(11)所示。其中ziq為無功量測值；wiq為無功量測權重；riq為無功量測殘差；

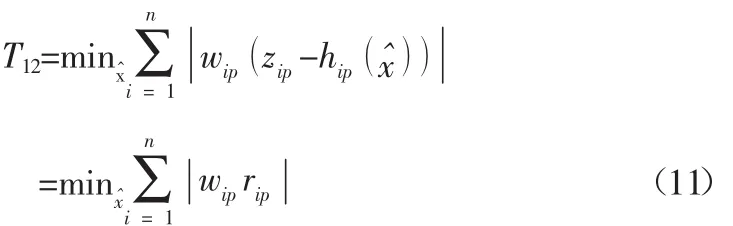
4）狀態估計總目標函數值T13

式（10）和式（11）中，n 為量測數目；x?為狀態量的估計值；h（x?）為第i個量測相對于狀態量估計值的非線性函數值。

4.2 狀態估計抵御粗差能力

采用式（9）～式（12）指標來衡量狀態估計計算精度，其結果如圖3和表1所示，其中Agri1為基于SCADA量測的加權最小二乘狀態估計，Agri2為本文所述的基于分段線性權函數的選權迭代狀態估計。

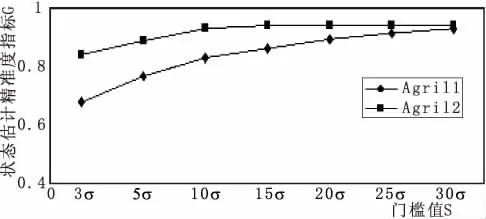
圖3 G指標曲線

圖3為邊界系數a取2.5，b取11.5，c取10.6時指標G的曲線。其中橫坐標表示門檻值s，取量測誤差標準差的整數倍；縱坐標為狀態估計精度指標G，取值為(0，1]。

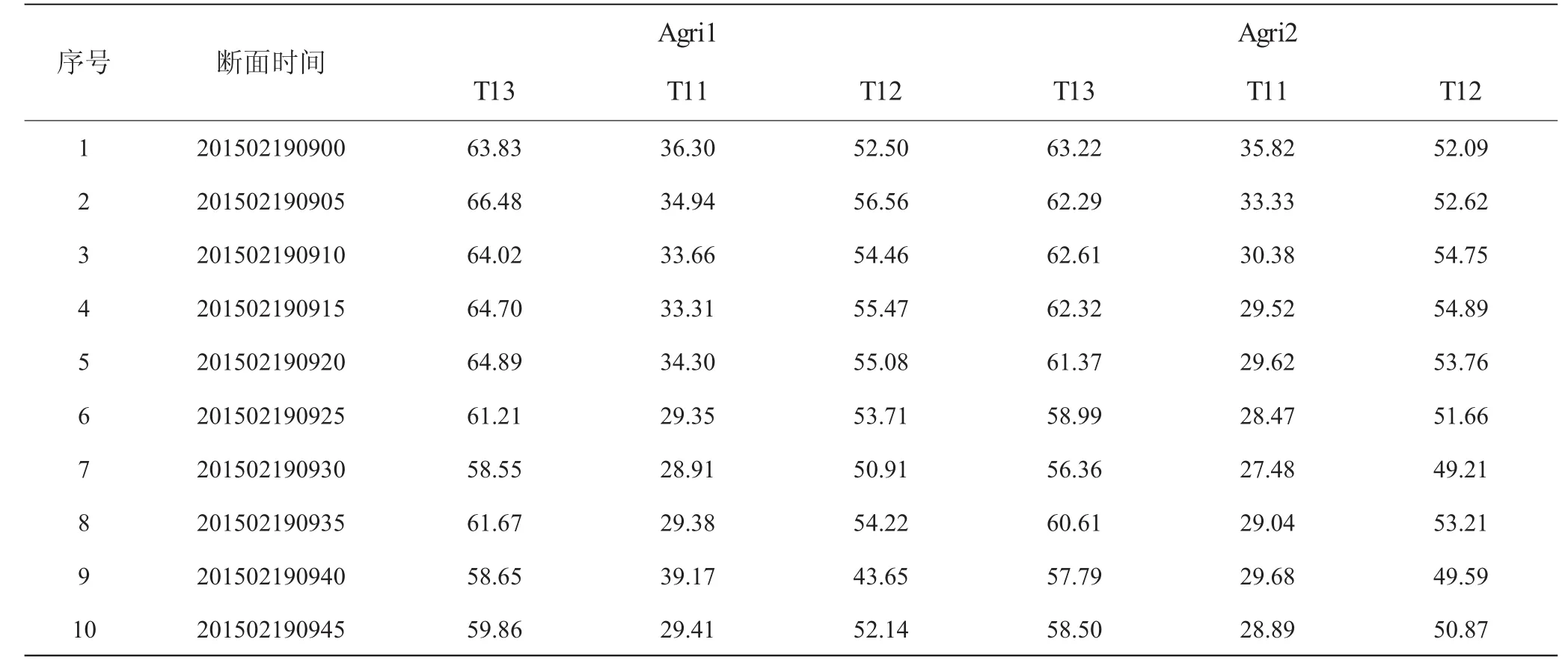
表1 不同時刻兩種算法的T11、T12、T13指標值

表1為不同時刻斷面下兩種算法的T11、T12、T13指標比較結果。其中量測斷面總數為10，按照狀態估計每5分鐘計算周期獲得。

從圖3的G曲線上可以看出，在量測系統粗差和正常量測均已確定的情況下，若狀態估計計算精度較高，則能使僅含粗差的量測殘差較大，而正常量測的殘差很小，G指標趨向于1；若狀態估計的精度較差，或者沒有能夠完全剔除所有量測系統粗差影響，則沒有被剔除粗差將對其他正常量測進行污染，導致正常量測的殘差上升，則G指標下降，如圖3中當門檻值取3時，此時加權最小二乘估計法的G指標為0.69，而采用本文方法后G指標為0.81，落在3門檻值以內的量測點數增多，算法所表現的抵御粗差能力更好，因此采用本文算法其估計精度較之傳統方法較好。

對于2015年2月19日9點5分的時間斷面上，采用本文方法后總體目標函數由66.48降為62.29，表明估計殘差進一步縮小。因此，從表1不同時間斷面指標所呈現的趨勢來看，在全局效果上，狀態估計的總目標函數、有功目標函數等性能指標相比傳統加權最小二乘估計方法減小，因而其估計的精度得以提高。

5 結語

通過智能電網調度試驗驗證平臺，采用基于線性分段權函數的選權迭代狀態估計方法后，由于權因子和量測量殘差動態相互關聯，有效的抑制了量測系統不良數據對估計結果的影響，使估計精度較之傳統加權最小二乘估計方法較好，能夠有效的排除系統粗差對水電站和電力系統數據量測狀態估計計算的干擾。

[1]周江文，黃幼才，楊元喜，等．抗差最小二乘法[M]．武漢：華中理工大學出版社，1997．

[2]周蘇荃，柳焯．新息圖法狀態估計[J]．繼電器，2000．

[3]孫宏斌，高峰，張伯明．電力系統最小信息損失狀態估計的信息學原理[J]．中國電機工程學報，2005．

[4]于爾鏗．電力系統狀態估計[M]．北京：水利電力出版社，1985.