偽單調均衡問題的一種加速投影算法
,
( 上海理工大學 管理學院,上海 200093)
1 問題的提出
均衡問題EP(f,C)[1]是:尋找點x*∈C,使對?y∈C,下面不等式成立:
f(x*,y)≥0
(1)
式中:C∈Rn是非空閉凸集,f:C×C→R為一個雙重函數,即對?x∈C,f(x,x)=0恒成立.
當f(x,y)=〈F(x),y-x〉,其中,F:C→Rn為一個連續函數,那么,EP(f,C)就轉化成變分不等式問題VI(F,C),即尋找點x*∈C,使對?y∈C,下面不等式成立:
〈F(x*),y-x〉≥0
(2)
顯然,f連續,F也連續.如果f關于x*∈C是偽單調的,則F關于x*∈C也是偽單調的.
EP(f,C)在電力市場、交通運輸、經濟及網絡等問題中都有廣泛的應用[2-5].求解EP(f,C)的方法主要有三類:a.近似點法,該方法由Martinet[6]提出并首次應用在求解VI(F,C),后來Moudafi[7]在假設映射f單調的前提下將該算法推廣到求解EP(f,C);b.gap函數法[8],利用連續可微的gap函數將EP(f,C)轉化為最優化問題,但是,算法的收斂性建立在f強單調的基礎上;c.輔助問題原理法,Cohen[9]提出x*∈C是EP(f,C)的一個解,當且僅當x*∈C是強凸問題
的唯一解,其中,ck>0,但這需要f強單調且Lipschitz連續.隨后,Antipin[10]在文獻[9]的基礎上,在每次迭代過程中增加一個外推步,提出了一種改進算法,具體過程如下:
式中:D是Bregman距離函數;C是一個多面凸集.
該算法減弱了f的單調性,其收斂性建立在f偽單調且Lipschitz連續的基礎上.
本文借助于輔助問題原理法,結合Solodov等[11]提出的求解變分不等式的改進投影算法,運用Armijo型線搜索,通過改進投影區域,使每次迭代結果更接近均衡問題的解.在f偽單調并連續(非Lipschitz連續)的前提下,證明了算法的收斂性.
2 預備知識
定義1設C?Rn,f:C×C→R∪{+}是雙重函數,
a.若對?x,y∈C,?ρ>0,使得f(x,y)+f(y,x)≤-ρ‖x-y‖2,則稱f在C上是強單調的.
b.若對?x,y∈C,f(x,y)+f(y,x)≤0,則稱f在C上是單調的.
c.若對?x,y∈C,f(x,y)≥0?f(y,x)≤0,則稱f在C上是偽單調的.
顯然,(1)?(2)?(3).
定義2若存在正常數c1,c2,使得f(x,y)+f(y,z)≥f(x,z)-c1‖x-y‖2-c2‖y-z‖2,則稱f在C上Lipschitz連續.
定義3設X?Rn,實值函數f:X→R,
a.若對?x,y∈X,?λ∈[0,1],有f(λx+(1-λ)y)≤max{f(x),f(y)},則稱f(x)為X上的擬凸函數.
b.若對?x,y∈X,〈f(y),x-y〉≥0蘊涵f(x)≥f(y),或者f(x) 定義4對?z∈C,?2f(z,z)表示凸函數f(z,·)在z處的次梯度,其中,?2f(z,z)滿足: 引理1[12]設PC(·)是C上的投影映射,則 a.‖PC(x)-PC(y)‖≤‖x-y‖,?x,y∈Rn; b.‖PC(x)-PC(y)‖2≤〈PC(x)-PC(y),x-y〉,?x,y∈Rn; c.〈x-PC(x),y-PC(y)〉≤0,?y∈C,x∈Rn; d.‖PC(x)-y‖2≤‖x-y‖2-‖PC(x)-x‖2,?y∈C,x∈Rn; e.‖PC(x)-PC(y)‖2≤‖x-y‖2-‖PC(x)-x+y-PC(y)‖2,?x,y∈Rn. 引理2[13]設f(x,y)關于y是Gateaux可微的,如果x*是EP(f,C)的解,即f(x*,y)≥0,?y∈C,則x*也是變分不等式〈G(x*),y-x*〉≥0,?y∈C的解,其中,G(x)=?f2(x,x).進一步,如果對每個x∈C,f(x,y)關于y是偽凸的,則逆命題也成立. 基于上述的理論基礎,現提出求解偽單調均衡問題的一種加速投影算法.該算法的基本思想是運用Armijo型線搜索得到一個預估點并以此構造一個超平面,進一步通過適當選擇步長和減小投影域使得算法產生的序列快速收斂.現介紹具體算法. 算法1 步驟1計算 令zk=xk-γmkrk,其中,mk是使得 〈?2f(zk,zk),rk〉≥σ‖rk‖2 的最小非負數. 步驟3令k=k+1,返回步驟1. 用SOL(f,C)表示均衡問題EP(f,C)的解集,由文獻[14],若f是連續的,則SOL(f,C)是閉合集合;若f是偽單調的,則SOL(f,C)是凸集.為了證明算法1的收斂性,首先作出如下假設: A1f在C上偽單調; A2f(x,y)是C×C上的連續可微凸函數且關于y是偽凸的,?2f(x,x)在C上是上半連續的; 根據上述假設可知,SOL(f,C)是一個閉凸集. 0∈?2f(x,x)+NC(xk) 其中,NC(xk)是xk處的外法向錐.因此,有 〈ωk,x-xk〉≥0,?x∈C (3) 其中,ωk∈?2f(x,x).由于f(xk,yk)是凸函數,則 (4) 結合式(3)和式(4),又因為,f(xk,xk)=0,所以,f(xk,x)≥0對?x∈C都成立,即xk是EP(f,C)的解. 定理2若rk≠0,則對?k≥0,存在非負數mk使得〈?2f(zk,zk),rk〉≥σ‖rk‖2成立. 證明假設〈?2f(zk,zk),rk〉-σ‖rk‖2<0,即有〈F(xk-γmkrk),xk-yk〉-σ‖rk‖2<0,因為,γ∈(0,1),當m→,取極限,根據f(x,y)的連續性,可以得到〈F(xk),xk-yk〉-σ‖rk‖2≤0. 由引理2,即 f(xk,yk)+σ‖rk‖2≥0 (5) 當y=xk時, (6) (7) 證明將xk+1代入式(7)的左邊,可得 由引理1和引理3可得 其中,第1個不等式由引理1得到,第2個不等式由偽單調條件得到.根據引理3,可得 ‖xk+1-x*‖2≤‖xk-x*‖2- 另一方面,由zk=xk-γmkrk,即xk-zk=γmk(xk-yk),顯然,由輔助問題原理,當k→時,所以, 當j→時,則有 因為,對?x∈C,f(x,x)=0恒成立,所以, 通過改進投影區域,給出了求解偽單調均衡問題的一種加速投影算法,由以上述證明可知,此算法不要求雙重函數f是Lipschitz連續的,且在偽單調條件下是全局收斂的. [1] GIANNESSI F,MAUGERI A,PARDALOS P M.Equilibrium problems:nonsmooth optimization and variational inequality models[M].Boston,MA:Springer,2001. [2] OLIVEIRA H A E JR.Coalition formation feasibility and Nash-Cournot equilibrium problems in electricity markets:a Fuzzy ASA approach[J].Applied Soft Computing,2015,35:1-12. [3] HO W,WONG S C,YING L B.Sequential optimization aproach for the mulit-class user equilibrium problem in continus transportation system[J].Journal of Advanced Transportation,2010,38(3):323-345. [4] BOGDAN M.Applications of parametric abstract equilibrium problems in economics[J].Procedia Economics and Finance,2012,3:99-104. [5] DE CEA J,FERNNDEZ J E,V DEKOCK,et al.Solving network equilibrium problems on multimodal urban transportation networks with multiple user classes[J].Transport Reviews,2005,25(3):293-317. [6] MARTINET B.Regularization d″inéquations variationnelles par approximations successives[J].Rev Fr Inform Rech Opér,1970,4(3):154-159. [7] MOUDAFI A.Proximal point algorithm extended to equilibrium problems[J].Journal of Natural Geometry,1997,15(1/2):91-100. [8] MASTROENI G.Gap functions for equilibrium problems[J].Journal of Global Optimization,2003,27(4):411-426. [9] COHEN G.Auxiliary problem principle extended to variational inequalities[J].Journal of Optimization Theory and Applications,1988,59(2):325-333. [10] ANTIPIN A S.The convergence of proximal methods to fixed points of extremal mappings and estimates of their rate of convergence[J].Computational Mathematics and Mathematical Physics,1995,35(5):539-551. [11] SOLODOV M V,SVAITER B F.A new projection method for variational inequality problems[J].SIAM Journal on Control and Optimization,1999,37(3):765-776. [12] ANH P N,LE THI H A.An Armijo-type method for pseudomonotone equilibrium problems and its applications[J].Journal of Global Optimization,2013,57(3):803-820. [13] 徐慶,朱道立,魯其輝.Nash均衡、變分不等式和廣義均衡問題的關系[J].管理科學學報,2005,8(3):1-7. [14] KONNOV I.Combined relaxation methods for variational inequalities[J].Berlin Heidelberg:Springer,2001:77-92. [15] WANG Y J,XIU N H,WANG C Y.Unified framework of extragradient-type methods for pseudomonotone variational inequalities[J].Journal of Optimization Theory and Applications,2001,111(3):641-656.3 加速投影算法
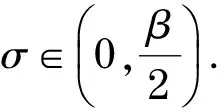
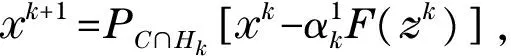
4 收斂性分析
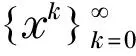
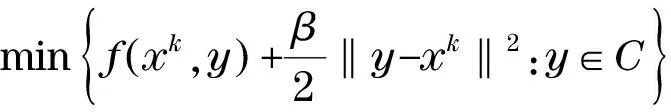
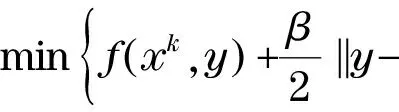
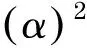

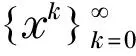
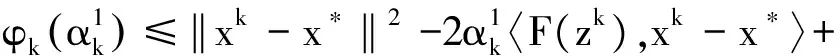
5 結 論

