基于引力模型的揚子江城市群中心城市選擇與影響范圍劃分

戴德頤

【摘 要】以2016年揚子江城市群人口和經濟數據為依據，運用引力模型和斷裂點理論為基礎，對揚子江城市群主要城市間經濟聯系結構和城鄉地區受輻射范圍進行研究。分析結果表明，南京和蘇州可分別作為揚子江城市群主要和次要中心城市，兩者輻射范圍大致以泰州、泰興到常州一線為界。

【關鍵詞】引力模型；揚子江城市群；中心城市；斷裂點理論

中圖分類號： F124.3；F224 文獻標識碼： A 文章編號： 2095-2457（2018）28-0290-003

DOI：10.19694/j.cnki.issn2095-2457.2018.28.136

江蘇沿江8市是全省區位優勢較為明顯的地區，經濟基礎好，明星城市多，要素資源豐富，曾經創造了聞名全國的“蘇南模式”。但是近年來隨著要素資源向中心城市集聚的趨勢加劇后，蘇南地區經濟增長日趨乏力，在高GDP數據背后，創新不足的問題也顯露出來，與廣東、浙江等地相比，江蘇雖然是經濟大省，卻不是創新經濟的強省。

2017年，江蘇省委、省政府出臺《關于加快建設揚子江城市群的意見》，提出到2020年，要將揚子江城市群基本建成整體聯動、分工有序、集聚高效的網格化城市群，隨后省委省政府多次強調，要將南京建設成為首位度高的省會城市，在揚子江城市群和寧鎮揚一體化中發揮龍頭帶動作用。江蘇省力求通過整合各地要素優勢，形成新的合力，助推全省經濟實現新的突破，并解決“有高原，無高峰”的困境。

目前，關于中心城市與城市群城市結構的問題，已經有眾多學者進行研究，包括核心城市中心度測度[1-2]、城市經濟空間結構分析[3-5]、中心城市影響范圍劃分[6-7]；從研究對象范圍大小來看，主要可分為全國性城市群，如長三角、珠三角、京津冀城市群、區域性城市群，如某個省份次級地域城市群；常用的研究方法主要有引力模型及改進的引力模型、城市影響范圍的斷裂點理論[6]、空間自相關理論等。現有研究中使用最多的引力模型，源自物理學中的萬有引力定律，指任意兩個物體之間均存在引力，引力大小與它們的質量乘積成正比，與它們之間的距離平方成反比。經過相關學者的引用和改進，最終形成了目前在區域經濟、地理經濟等學科領域最為常見的引力理論。自該方法傳入國內以后，眾多城市經濟領域的學者也紛紛進行了相關研究，常用人口、GDP規模來表示城市的質量，考慮到現在交通、信息科技的飛速發展，幾何意義上的距離已經不能準確反映城市之間的空間結構，簡單用GDP等指標也很難概括城市的質量，因此，很多學者選擇新的指標進行研究，從多個維度來衡量城市的綜合實力及城市之間的距離。在高鐵時代，交通時間與交通成本也被納入距離因素。本研究擬運用引力模型和斷裂點理論，在測度揚子江城市群各城市間引力值的基礎上，量化各城市的影響等級，并劃分城市群區域城鄉地區受輻射范圍，為揚子江城市群建設及城鄉協調發展提供理論依據。

1 揚子江城市群概況與研究方法

1.1 揚子江城市群概況

揚子江城市群地處江蘇省長江沿岸，包括南京、蘇州、無錫、常州、鎮江、揚州、泰州、南通等8個省轄市，及其所轄區、縣、縣級市。該區域地理位置優越，自古以來便是我國經濟文化發達地區，境內河湖密布，平原為主，水運便利，有“黃金水道”之稱的長江下游流經該地入海，水運吞吐量占全長江九成以上，長江南京以下12.5米深水航道竣工后，更是大幅提高了境內的水運能力。就全國來說，揚子江城市群綜合條件在同類型城市群中居于前列。

2016年，揚子江城市群以大約5萬平方公里的國土面積，集聚了近5千萬常住人口，創造GDP逾6萬億元，該數值在各省級行政區中僅次于廣東、江蘇與山東三省；人均GDP達120773元，超過全國所有省級行政區，也高于京、津、滬三大直轄市；金融機構存款余額102580.9億元，僅次于廣東、北京和上海。各項數據均有力顯示，揚子江城市群是世界級長三角城市群的主要組成部分，也在長江經濟帶戰略中占據重要地位。

1.2 引力模型

參考物理學中的萬有引力模型，在國際貿易中，相關學者借鑒了萬有引力模型，提出不同國家之間的貿易量與兩國之間的距離平方成反比，與兩國經濟總量的乘積成正比。在經濟地理領域，學者經過轉換，提出與之類似的城市間經濟流量計算模型，認為兩個城市之間的引力與各自城市的質量乘積成占比，與城市間距離的某個次方成反比。

公式（1）是經濟地理中常見的引力模型，其中Fij表示i城市與j城市之間的經濟流量，K表示引力系數，Qi、Qj分別表示i和j城市的質量，dij表示兩地之間的距離，r表示距離衰減系數。有研究表明，距離衰減系數通常在0.5-3之間，考慮到當前交通條件日益發達，空間距離的相對重要性已不像早期那么重要，因此，本文將距離衰減系數定位1，引力系數也按照慣例取1。

引力值大小反映城市之間經濟聯系的強度，值越大，說明兩城市間經濟聯系越緊密；反之，說明兩地間經濟聯系較少。城市群研究中，常用引力值的大小來反映兩城市間的互動關系，只有與區域內多數城市都有較高引力值的城市，才會成為該區域的中心城市；同時，只有城市群各城市間經濟聯系普遍密切，該城市群才是發展較為成熟的城市群。

1.3 斷裂點理論

1949年康弗斯（P.D.Converse）在“零售引力規律”的基礎上，提出了斷裂點理論。斷裂點理論認為，城市的影響范圍由該城市的規模和相鄰兩城市間的距離決定，某個城市規模越大，綜合實力越強，該城市的影響范圍就越大，反之則越小，相鄰兩城市的吸引力剛好達到彼此相等的點，叫做斷裂點[6]。斷裂點公式為：

其中，Dc表示斷裂點到核心城市c的距離，Dce表示核心城市c和核心城市e之間的距離，Ge和Gc分別表示城市e和c的綜合實力。

2 實證分析

2.1 引力值計算

城市之間引力值計算主要涉及城市質量Q和城市之間距離r。以往研究中，常用城市人口或GDP代表城市質量，但過去的研究經驗表明，單純用人口或GDP并不能很好的表征城市質量，因此，本文采用人口與GDP的乘積，結果取根號表示城市的質量。需要注意的是，因我國城市概念比較模糊，有行政轄區意義上的城市，也有純市區概念的城市，從經濟地理意義上來說，市區概念更符合引力模型的范疇，因此，本文我們取市區概念的城市，人口及GDP均按照市區口徑，省轄市不計算下轄縣及縣級市的數據。同理，在GDP和人口數據上，我們認為市區應該是以第二、第三產業為絕對主導，所以，我們取市區第二和第三產業增加值作為市區GDP指標，取市區第二和第三產業就業人口作為市區人口指標。城市之間的距離按照兩城市之間百度地圖的推薦路線計算。

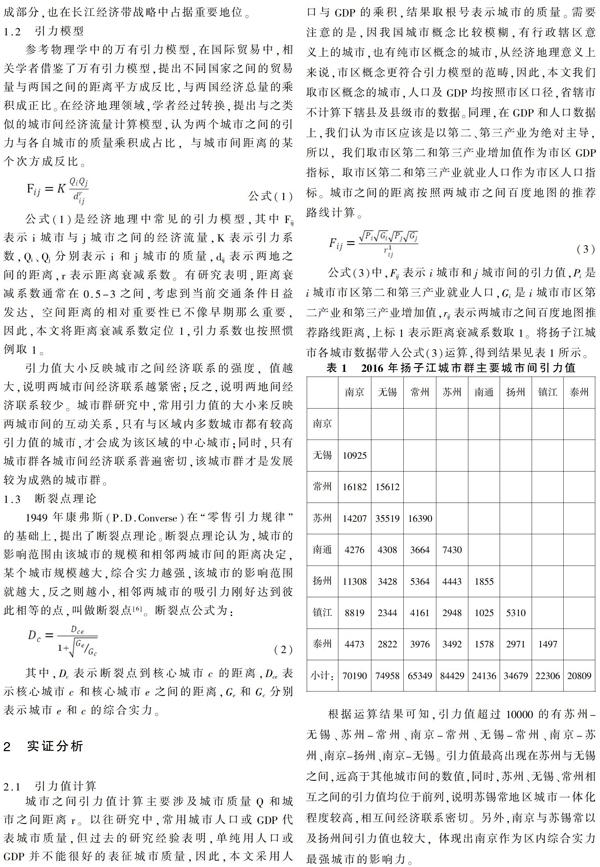
公式（3）中，Fij表示i城市和j城市間的引力值，Pi是i城市市區第二和第三產業就業人口，Gi是i城市市區第二產業和第三產業增加值，rij表示兩城市之間百度地圖推薦路線距離，上標1表示距離衰減系數取1。將揚子江城市各城市數據帶入公式（3）運算，得到結果見表1所示。

根據運算結果可知，引力值超過10000的有蘇州-無錫、蘇州-常州、南京-常州、無錫-常州、南京-蘇州、南京-揚州、南京-無錫。引力值最高出現在蘇州與無錫之間，遠高于其他城市間的數值，同時，蘇州、無錫、常州相互之間的引力值均位于前列，說明蘇錫常地區城市一體化程度較高，相互間經濟聯系密切。另外，南京與蘇錫常以及揚州間引力值也較大，體現出南京作為區內綜合實力最強城市的影響力。

表2顯示列出了揚子江城市群各主要城市互動聯系前三位城市。蘇州、南京分別有3次位居第一，無錫、常州分別有1次位居第一。但是對區域內所有城市來說，南京都居于引力值排名前三位，而蘇州并未列入揚州和鎮江的引力值前三位城市。因此，從經濟聯系范圍的廣度來看，南京超過蘇州，成為揚子江城市群首選中心城市。蘇州則是區域內蘇錫常次級區域的中心城市，對周邊城市起到有力帶動作用。

2.2 斷裂點計算

在運用公式（2）計算各個城市的斷裂點時，城市間距離（Dce）、城市e和城市c的實力（Ge、Gc）所采用的數據均與引力模型計算中要求一致。參考2.1部分計算的引力值，本文認為揚子江城市群中具備做中心城市的備選名單有南京、蘇州、常州、揚州，無錫因為與蘇州過近，且只出現在3個城市的引力值前三位，故不適合作為中心城市。揚州是該區域長江以北總引力值最大城市，因此，也放入備選名單。

斷裂點計算結果顯示，南京與常州之間的斷裂點距離南京75.66千米，距離常州53.33千米。也就是說，從影響力來說，南京能夠影響到越過鎮江，接近丹陽的位置，常州影響力略微超過丹陽，不到鎮江。南京與蘇州的斷裂點位于距南京116.44千米處，距離蘇州99.54千米，位于常州市西郊，這與傳統蘇錫常的影響范圍一致。南京與揚州的斷裂點距南京市69.1千米，距揚州市36.91千米，大致位于儀征市。蘇州與常州的斷裂點距蘇州50.96千米，距常州42.04千米，大約位于無錫市惠山區，說明無錫更接近蘇州的輻射范圍，而常州主要輻射自身轄區。蘇州與揚州間斷裂點距蘇州121.23千米，距揚州75.77千米，蘇州影響范圍大致可到泰州泰興市及鎮江市東部邊界。

根據斷裂點計算結果，可以知道揚子江城市群城鄉區域受輻射范圍的結構劃分，輻射范圍最大的是南京和蘇州，其中南京的輻射范圍大致到達常州市及泰州市，覆蓋揚州市、鎮江市全境及泰州市和常州市西部區域；蘇州輻射范圍向西到達常州市區，向北到達泰州泰興市，覆蓋無錫、南通全市及常州中東部、泰州東部區域。常州和揚州輻射范圍主要在本市范圍內。

3 結論

本文通過改進后的引力模型和斷裂點模型，構建了衡量揚子江城市群城市間引力值的評價體系，計算了主要城市間斷裂點值，計算結果與揚子江城市群實際情況基本符合，說明該評價方法客觀可行。計算結果說明，南京最適宜做為揚子江城市群中心城市，其輻射范圍最廣，蘇州與周邊的無錫、常州聯系緊密，可以作為次區域中心城市。但對于南京來說，也存在引力值偏低的問題，如要更好帶動整個區域發展，尚需繼續提高城市綜合實力，并有效擴展城市邊界，縮短與其他城市空間距離。

為促進揚子江城市群城鄉一體化發展，可分別以南京為中心、蘇州為次中心，輻射帶動整個城市群發展。建立城鄉一體化的要素雙向流動機制，通過中心城市——中等城市——小城鎮——鄉村的發展路徑，加大區域內綜合交通體系建設，逐步將小城鎮及鄉村地區納入大城市的公共服務體系中，切實提高農民生活水平；轉移農村富余勞動力到城市中就業，并可利用生活成本低、土地資源豐富的優勢，承接部分大中城市的簡單加工、休閑旅游等項目。通過上述措施，形成以點帶線，以線到面，最終建立以工促農、城鄉互補的城市群發展新經驗。

【參考文獻】

[1]姚永玲，唐彥哲.城市群首位城市的聯系能級、中心度和控制力[J].經濟地理，2015，35（7）：66-72.

[2]王錄倉，嚴樹娟，王靜.欠發達地區城市流強度及中心度研究—以甘肅省為例[J].現代城市研究，2016，04：95-99.

[3]王海江等.我國省域經濟聯系的空間格局及其變化[J].經濟地理，2012，32（7）：18-23.

[4]何勝，唐承麗，周國華.長江中游城市群空間相互作用研究[J].經濟地理，2014，34（4）：46-53.

[5]張樂，馬永俊.浙中城市群核心城市經濟聯系強度及影響因素[J].湖南師范大學自然科學學報，2013，（3）：85-89.

[6]方大春，孫明月.長江經濟帶核心城市影響力研究[J].經濟地理，2015，35（1）：76-81.

[7]張利利，佘濟云，李銳，陳冬洋.基于引力模型的城鄉交錯帶空間邊界界定研究[J].中南林業科技大學學報，2017，37（1）：99-104.