基于神經網絡的模擬電路故障診斷
胡婕


摘要:為了提高RBF神經網絡進行模擬電路故障診斷的速度與準確性,提出了一種基于小波變換、主成分分析與RBF神經網絡相結合的故障診斷算法。該算法首先利用小波變換提取模擬電路的故障信號特征,然后利用主成分分析達到降維的目的”從而達到精確識別故障類別的目的。最后選用Sallen-Key帶通濾波器作為實驗對象進行測試,測試結果表明該方法能精確識別模擬電路的故障類別,從而起到故障診斷,為后續電路的處理指明方向。
關鍵詞:RBF神經網絡;小波變換;主成分分析;故障診斷
0 引言
模擬電路廣泛應用于通訊、自動控制,家用電器等各個方面,隨著電子技術的迅猛發展,模擬電路的復雜度和密集度不斷增長,因些我們對于模擬電路是否能可靠運行提出更加嚴格的要求。因此,近年來各種基于人工智能算法的模擬電路故障診斷方法成為了故障診斷的研究熱點。
1 RBF神經網絡
RBF神經網絡(Radial Basis Function Neural Net-work,RBFNN)的結構示意圖如圖1所示,它是一種三層前饋網絡,由輸入層、隱含層和輸出層組成。
RBF神經網絡由n個輸入節點、h個隱節層節點和m個輸出層節點構成。其中第i個隱節點的激活函數為Φi(*),這個函數也稱為徑向基函數。徑向基函數有多種表示形式,這里我們采用Gaussian函數,即。輸出層的藝表示神經元的激活函數為線性函數。
RBF神經網絡的第k個輸出為:
RBF神經網絡具有自學習、自組織、自適應能力,與BP神經網絡相比,它不僅具有某些生物神經元的近興奮、遠抑制的生理學基礎,而且結構更簡單,學習速度也更快,具有更強的生命力。目前,RBF神經網絡已經成功地應用于數據分類、模式識別、系統建模和故障診斷等領域。
2 改進的RBF神經網絡診斷模型
本文在前人的基礎上進行了一些改進,主要體現在:(1)對原始數據采用小波變換進行預處理,從而獲得故障特征能量譜,并進一步構造特征向量;(2)采用主成分分析對特征數據進行處理從而達到降低維度的目的;(3)結合小波變換、主成分分析及RBF神經網絡對模擬電路進行故障診斷。
2.1 小波變換
小波變換是一種新的變換分析方法,它繼承和發展了短時傅立葉變換局部化的思想,同時又克服了窗口大小不隨頻率變化等缺點,能夠提供一個隨頻率改變的“時間一頻率”窗口,是進行信號時頻分析和處理的理想工具。小波變換的基本思想就是用一族函數去表示或逼近一個信號,這一族函數成為小波函數系。小波變換就是通過這一基本小波函數的不同尺度的平移和伸縮構成的。
小波變換的表達式如式(2)所示:
(2)式中:f(t)為待測信號;φ(t)為小波基函數;a為尺度并且a>0。
我們把待測信號f(t)分解成高頻信號和低頻信號,因此2層小波可分解成如圖2所示。
利用小波變換,我們對原始故障信號進行處理,從而得到故障特征向量,它是由分解系數的能量值所構成,具體過程如下所示:
(1)首先我們對原始故障信號進行小波變換,得到如下數據:
AN,D1,D2,…,DN
(2)將得到的數據序列求取平方和從而得到特征能量譜,繼而我們可以得到特征向量,即F=(EAN,ED1,ED2,…,EDN)
2.2 主成分分析
主成分分析法(Principal Component Analysis,簡稱PCA)是最古老的多元統計分析方法之一。它可以將數據從高維數據空間變換到低維數據空間,從而達到數據的特征及壓縮。
當模擬電路發生故障時,必然表現出與之對應的故障特征,為了全面反映電路實際的運行狀態,我們必然將從不同角度觀測到的故障特征盡可能完整地記錄下來。但這具有一定的不足,即故障特征中變量的維數過高,從而導致后面神經網絡結構復雜、訓練精度降低等缺點。為此,為了解決上述的問題,我們可以采用主成分分析方法對故障特征變量進行數據壓縮,從而構成故障特征新的樣本集。
具體做法如下所示:
(1)對經過小波變換后的數據進行標準化處理;
(2)將上面得到的數據變換成協方差矩陣;
(3)求取協方差矩陣的特征向量;
(4)計算特征向量的貢獻率;
(5)選取貢獻率較大的特征向量為故障特征向量,從而做為RBF神經網絡的輸入數據。
2.3 RBF神經網絡算法
RBF神經網絡的學習算法分為以下三個方面:
(1)確定隱含層由多少個神經元構成;
(2)求取隱含層節點的數據中心hi及其對應的徑向基函數擴展常數;
(3)修正輸出權值。
本文采用K-means聚類的學習算法,該算法也同樣適應于對模擬電路故障特征進行聚類。其具體算法如下:
(1)對算法進行初始化:我們在這里選取h個不同的聚類中心,并且令k=1。
(2)采用‖Xj-hi(k)‖,i=1,2,…,h,j=1,2,…,n此式計算聚類中心與樣本輸入之間的歐式距離。
(3)通過最小距離對Xj進行分類。
(4)重新計算hi(k+1)。
(5)若hi(k+1)≠hi(k),則轉到第2步,否則轉到步驟6,即停止聚類。
(6)確定隱節點的擴展常數,即δi=κdi,其中di,κ為重疊系數。
3 改進的RBF神經網絡故障診斷
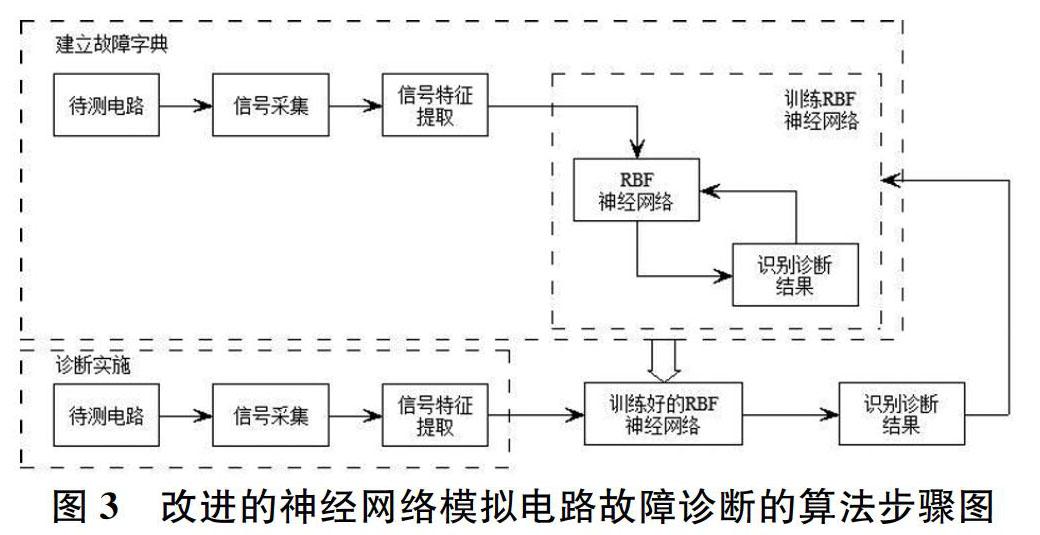
基于改進的RBF神經網絡的模擬電路故障診斷類似故障字典法,即先建立字典庫,故障診斷過程則稱為“查字典”。結合小波變換、主成分分析和RBF神經網絡,改進的神經網絡模擬電路故障診斷的算法步驟如圖3所示。
從圖3我們可以看出,RBF神經網絡的故障診斷由建立故障字典階段即學習過程和診斷實施階段這兩部分組成。首先我們需要對故障建立字典,也就是說我們需要對各種故障電路和無故障電路進行仿真,對模擬電路的輸出響應信號進行小波變換和主成分分析從而提取到模擬電路的故障特征,從而得到訓練樣本并訓練RBF神經網絡。當我們對模擬電路進行故障診斷時,對實測模擬電路施加同樣的激勵,然后對輸出響應進行進行小波變換和主成分分析,從而提取到模擬電路的故障特征,最后我們將這些故障特征輸入之前已經訓練好的神經網絡,從而可以診斷出模擬電路是出了哪種故障。
4 實驗與分析
本文提出了基于小波變換、主成分分析和RBF神經網絡相結合的模擬電路故障診斷算法,并將此算法應用于Sallen-Key帶通濾波器,來檢驗這種算法進行模擬電路故障診斷的準確率。Sallen-Key帶通濾波器電路圖如圖4所示,其中電阻具有±5%的容差范圍,電容具有±10%的容差范圍。此電路中的R2,R3,C1,C2這四個元件對頻率影響最為明顯,因此我們選擇R2,R3,C1,C2為被診斷元器件,可獲得R2(1±50%)、R3(1±50%)、C1(1±50%)、C2(1±50%)以及無故障這9種狀態。故障分類表如表1所示。
我們對5allen-Key帶通濾波器進行故障診斷時,選用幅值為5V,持續時間為10μs的脈沖序列,然后對該電路每種故障各進行60次蒙特卡羅分析,9種故障狀態可以得到540種故障數據。我們先將1-9種故障的30組訓練樣本特征向量輸入RBF神經網絡診斷系統,從而得到最優狀態的RBF神經網絡,然后將余下的3。組故障數據輸入訓練好的RBF神經網絡,即可以得到診斷率。故障數據如果沒有經過小波變換和主成分分析,直接通過傳統的RBF神經網絡,我們也進行了仿真實驗。這二種情況的診斷率如表2所示。對比模擬電路故障診斷結果如表2所示,我們發現經過小波變換和主成分分析后得到的故障特征數據再經過RBF神經網絡得到的診斷率要明顯優于直接經過傳統的RBF神經網絡的診斷率。
4 結論
實驗結果表明,基于小波變換、主成分分析和RBF神經網絡相結合的模擬電路故障診斷方法有較高的診斷率,該方法能精確地表明模擬電路的實際狀態,可以為模擬電路的故障診斷提供較好的依據。
參考文獻
[1]Coifman RR Wavelct analysis and signal mcessing[J].ActaPetmlogiea Et Mineralogica,1992,9(3):765-780.
[2]李明.基于多元統計分析的故障診斷方法及其應用研究[D].濟南:山東大學,2006.
[3]郝春燕等.基于神經網絡的模擬電路故障診斷方法[J].工亞控制計算機,2018,31(6):63-65.
[4]馬峻等.MRA-PCA-PSO組合優化BP神經網絡模擬龜路故障診斷研究[J].電子測量與儀器學,2018,32(3):73-78.
[5]李論等,基于小波變換多分辨率特征提取的模擬電路故障診斷方法研究[J].計算機與現代化,2012,(9):181-183,189.
[6]王艷等.基于小波包神經網絡的模擬電路故障診斷[J].電腦與信息技術,2014,22(6):22-25.

