基于動態面的微型撲翼飛行器縱向控制

董維中，崔 龍，王志東，2

（1.中國科學院大學 中國科學院沈陽自動化研究所 機器人學國家重點實驗室，沈陽 110016；2.日本千葉工業大學 先進機器人系，千葉 日本）

微型撲翼飛行器模仿昆蟲飛行，通過左右翅翼的高頻撲動產生推力、升力。國內外研究結果表明[1-2]，在小尺寸飛行器中，撲翼飛行的效率明顯高于固定翼、旋翼方式。撲翼飛行器可以靈活地懸停、倒飛、側飛等，其令人矚目的操縱性使得微型撲翼飛行器具有令人振奮的軍事、民用研究前景。

文獻[3-4]的實驗結果表明，撲翼飛行器的氣動力產生機制總結為延遲失速、旋轉環量、尾跡捕獲等，這些結論已經形成經驗公式。國外一些著名的項目組已經開展并得到了重要的研究成果。其中，斯坦福大學MFI項目和哈佛大學的Wood項目組等接近完成了實用撲翼飛行器的開發研究。

撲翼飛行器涉及了多學科交叉研究，包括微型機械設計、新型材料、流體力學、控制、電子、通信等學科和工程領域。在此，介紹撲翼飛行器總體設計，給出飛行器氣動力的計算；建立飛行器縱向模型，設計縱向控制器；針對懸停狀態進行仿真驗證。

1 微型撲翼飛行器

1.1 飛行器的總體設計

給出了一種微型撲翼飛行器的總體設計[5-6]，如圖1所示，飛行器主要由碳纖維機體、傳動機構、X型翼、微型電機、機載電路板等組成。

圖1 微型仿昆蟲撲翼飛行器Fig.1 Miniature insect like flapping wing aircraft

必須指出的是，從工程角度來看，X型翅翼擁有較高的效率并且制造難度最低，它只在上下方向單自由度地撲動。另外，由于翅翼所采用的高性能薄膜具有很高的柔性，從而使它能夠輕易地被流場改變形狀而產生推力。

機體采用碳纖維減輕了機體質量，連接部件采用柔性鉸鏈，如圖2所示。

不同于其他項目組采用人工肌肉的驅動方式，該飛行器仍然采用微型直流電機，電機安裝在飛行器機體質心。這種方式與荷蘭的DELFLY2飛行器相同。所采用的無刷直流電機內部結構如圖3所示。

圖2 柔性鉸鏈Fig.2 Flexure hinge

圖3 電機的內部結構Fig.3 Internal structure of motor

通過擴大機翼面積，提升了飛行器升力，從而具備一定程度的負載能力，其最重要的負載是機載電路板。該板安裝在機體上，只為完成人工遙控操作。其主要功能是與地面遙控器進行通信，從而控制微型電機。機載電路板的核心是一塊51單片機，它作為中央處理器負責通信信息解碼，并對微型電機進行控制。

需要指出的是，遙控飛行的目的是對總體設計進行室內飛行驗證。

遙控飛行的操作過程如下：地面人員操作遙控器的搖桿，搖桿的偏轉信息經過遙控器的芯片編碼后無線發送至機載電路板；信號經過電路板的天線，輸出給耦合共振芯片，然后經過數字轉換，再送入單片機；單片機隨之完成對地面搖桿信息的解算，之后形成電機指令送至功率芯片，最后變為電流信號控制電機轉速，由此保證飛機按照地面操作員的指令進行機動。機載電路板實物如圖4所示。

圖4 機載電路板實物Fig.4 Airborne circuit board material

所用機載電路板由中國科學院數學與系統研究院研制，其金屬部分為電路板的接收電線，能夠在50 m的半徑之內操縱飛行器飛行。

1.2 飛行器的氣動力計算

要建立飛行器數學模型，需先計算飛行器周圍流場作用在翅翼上的氣動力，這是撲翼飛行器研究非常重要的難點之一。氣動力計算公式[6]如下：

經過數值分析，給出準穩態氣動力計算歸一化處理結果為

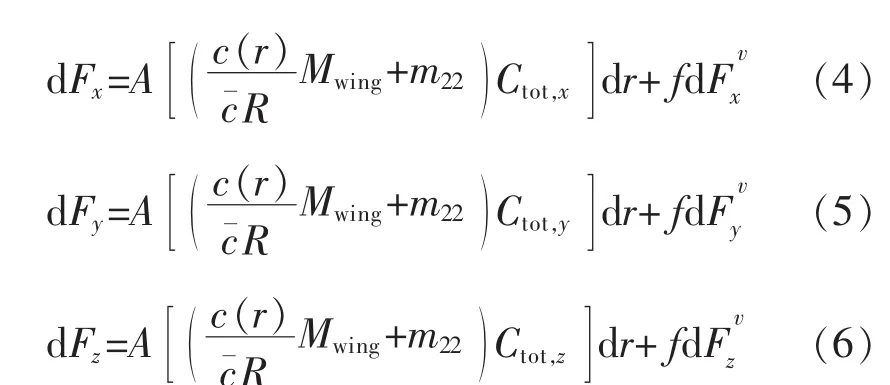
式中：A，f分別為翅翼的撲動角幅值和撲動頻率。通過改變A，f來影響氣動力的變化。在此，控制目標就是控制歸一化數值模型中的撲動角幅值A和頻率f，以直接操縱飛行器。

2 飛行器的縱向數學模型

在此，縱向模型的前提是不涉及縱向控制中的高度通道，也不針對橫滾、偏航等方向，只針對縱向控制中最重要的俯仰角控制；相對于機體，翅翼的質量忽略不計。

采用Newton-Euler原理建立動力學方程，根據動量矩定理，有

式中：L，M，N分別為飛行器在滾轉、偏航、俯仰方向所受到的力矩；p，q，r為滾轉、偏航、俯仰方向的轉動速率。 式（7）、式（8）均不涉及縱向控制，故不給予考慮。

根據俯仰角定義

式（10）的直觀解釋是：俯仰角在一定時間內的偏轉就是俯仰角速率。

另外，根據飛行控制理論，式（9）中滾轉、偏航的轉動速率p和q在俯仰控制時變化緩慢，因而可以忽略。

最后，給出縱向控制模型，它僅描述控制力矩和飛行器俯仰角速率之間的映射關系，即

3 飛行器縱向穩定控制

傳統PID控制方法對于復雜非線性系統來說，控制效果較差，在此引入動態面控制方法。為了提高控制效果，把俯仰角控制分為內回路的俯仰角速率控制和外回路的俯仰角控制。

以下驗證在懸停模態下，飛行器在縱向方向的穩定問題。控制變量為撲動頻率f和撲動角幅值A，而控制的目標是飛行器在x方向上的位置、z方向上的位置和俯仰角輸出。在此僅詳述俯仰角控制律設計過程。在完成俯仰角控制器后，只對時間積分就能得到縱向平面的位置控制器，故不再贅述。需要說明，縱向位置控制也直接依賴于撲動角幅值A和頻率f。

首先給出已定義的俯仰角模型式（11）。

步驟 1定義 e?=?-?d，則有

步驟2定義1個滑動面

步驟3定義1個Lyapunov函數

對式（14）求導，得

步驟4定義

針對r，設計估計值為

為了解決使用反演法而產生的問題，引入一階濾波器，即

式中：α?（0）=rˉ（0）；τ?為濾波常數。 故可得

一階濾波器的選擇是為了便于實現，定義濾波誤差為

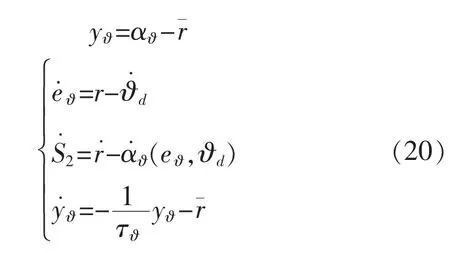
假設外部擾動力矩變化緩慢，構造1個聯合Lyapunov函數

對其求導，得

針對式（22），設計控制器為

把式（23）代入式（22），得到

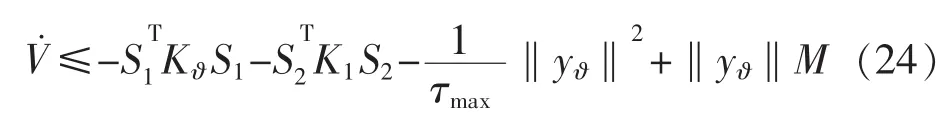
根據Young不等式，得到

最后得到

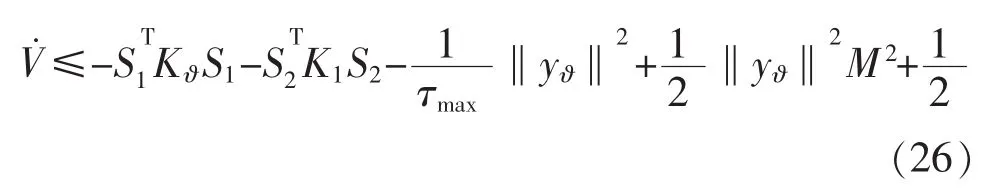
由式（26）可知，系統在動態面控制器的作用下，能夠在有限的時間內收斂到1個小區域內，因此控制策略是有效的。

對于撲動角幅值和撲動頻率控制律的設計，由于

式中：N為俯仰力矩，由氣動力Fx，Fz乘以作用力臂得到。而氣動力Fx，Fz直接由撲動角幅值A和頻率f決定，因此控制律如式（23）所示，通過這種直接控制方法可以完成對俯仰通道的控制。

4 半物理仿真實驗

[7]的仿真實驗過程，模擬在懸停狀態下的縱向位置和俯仰角鎮定。

設定平衡點為（0，0），為飛行器輸入設定跟蹤值 xd=0 m，zd=0 m，q=4°。

仿真實驗結果即飛行器縱向位置輸出數據，如圖5所示。

圖5 飛行器縱向x，z位置輸出Fig.5 Aircraft longitudinal x，z position outputs

由圖可見，飛行器能夠在有限的時間內迅速收斂，其位置輸出穩態收斂在0點附近。根據計算，系統輸出誤差最高為0.4%，達到控制要求。

縱向仿真第3個輸出量為俯仰角，其數據如圖6所示。

圖6 飛行器俯仰角輸出Fig.6 Aircraft pitch angle output

由圖可見，系統在懸停狀態下，機體俯仰角圍繞機體軸，會呈現一定的擺動，擺動的偏差最高達到0.3%，基本滿足要求。

半物理實驗同時進行了高速攝影位置拍攝。在拍攝過程中，飛行器姿態無明顯變化，基本保持穩定，如圖7所示。這說明在飛行器總體設計合理，具有較高的靜穩定性。

圖7 飛行器姿態基本保持穩定Fig.7 Aircraft attitude remains stable basically

5 結語

所完成的總體設計在室內測試中基本達到對飛行時間的要求，說明其總體設計方案中的X型翼能夠提供足夠的升力，滿足加載機載電路板的要求；采用經驗公式計算飛行器的氣動力，實現了較高的逼近精度；在縱向俯仰角和位置控制的仿真試驗中，所研制的基于動態面控制律是有效的，在位置和俯仰角輸出上表現出較高的穩定性和較小的控制誤差。關于撲翼飛行器縱向控制的研究成果為下一步開展全自主飛行打下了基礎。

參考文獻：

[1]袁昌盛，李永澤，譚健.微撲翼飛行器控制系統相關技術研究進展[J].計算機測量與控制，2011，19（7）：1527-1529.

[2]Ramamurti R，Sandberg W C.A three dimensional computational study of the aerodynamic mechanisms of insect flight[J].Journal of Experimental Biology，2002，60（18）：110–118.

[3]Weis-Fogh T.Quick estimates of flight fitness in hovering animals including novel mechanisms for lift production[J].J Exp Biol，1973，59（1）：169-230.

[4]Ellington C P.The aerodynamics of hovering insect flight IV：Aero-dynamic Mechanisms[J].Phil Trans R Sco Land，1984，305（1122）：145-185.

[5]Orlowski C，Girard A，SHYY W.Four wing flapping wing micro air vehicles[C]//Proceedings of the 2010 AIAA Guidance，Navigation and Control Conference.AIAA，2012.

[6]Gordon J，Berman Z，WANG JANE.Energy-minimizing kinematics in hovering insect flight[J].J Fluid Mech，2012，582：153-168.

[7]杜亞娟.半實物仿真綜合實驗臺控制系統方案[J].計算機工程，2010，36（22）：233-235.