工業余熱制冷系統溫度傳感器測量準確性校正

周 剛，楊永平

（陜西理工大學 陜西省工業自動化重點試驗室，漢中 723000）

當今社會，空調已經成為人們生活中不可缺少的部分，空調需求巨大的增加，給環境和能源帶來了巨大的壓力。因此，研發出了工業余熱吸收式制冷機組，它利用工業中低溫廢水、廢氣作為主要驅動能源，具有環保節能功效，制冷效果也好。由于得不到準確的工業余熱吸收式制冷系統最基本的溫度參數，使得工業余熱吸收式制冷系統的效率得不到有效的提高。

1 Cu50溫度傳感器數據的標定

在眾多Cu系列的傳感器之中，Cu50溫度傳感器測量精度很高，測量范圍在-50℃～+150℃之間比較正確，廣泛應用于工業余熱吸收式制冷系統的發生器、吸收器中。所以檢測就選用0～100℃的范圍，依次改變恒溫箱的溫度進行檢測。在實際應用中，首先對其進行T-R特性校正，常用方法有：（1）PB運算法[1-2]，該方法收斂速度慢，容易陷入局部極小而得不到全局最優值，計算結果誤差太大，對于網絡的隱節點數選取沒有理論指導；（2）硬件補償算法[3-4]，這種方法是對其測量電路進行校正補償，雖然精度高，但操作復雜；（3）神經網絡算法[5-6]，這種方法運算量大、速度慢，容易陷入局部極小而得不到全局最優值，精度不高。為了保證數據的擬合精度和有效地查看擬合效果，利用最小二乘法將測量數據分成4段，分別進行一次、二次、三次、四次擬合，該方法比較簡單，通過擬合精度評估和在工業余熱吸收式制冷系統的應用中驗證了該方法精度高。工業余熱吸收式制冷系統的吸收器、發生器研究的溫度范圍通常在10～100℃，所以可以在這個研究范圍進行檢測，可以采用恒溫箱來控制溫度，改變恒溫箱溫度進行測量，采用四線制結法對Cu50熱電阻進行連接，用安捷倫表對Cu50熱電阻隨溫度變化而對應的電阻值進行測量，用精度高的數字溫度計測量它的實際溫度。圖1為試驗系統示意圖，圖2為實際測量的數據曲線。

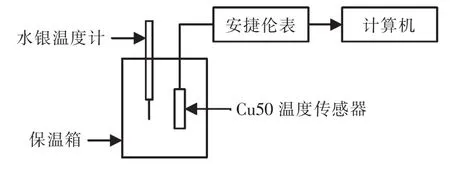
圖1 試驗系統示意Fig.1 Schematic of the test system

圖2 Cu50熱電阻溫度傳感器T-R的實測數據的關系曲線Fig.2 Cu50 temperature sensor’s T-R relation curve of the actually measured data

由圖2曲線可看出Cu50溫度傳感器具有非線性的特征，可以得出傳統的校正方程，由文獻[7]可知，Cu50溫度傳感器的溫度和電阻關系（在-50℃～150℃）之間的校正方程為

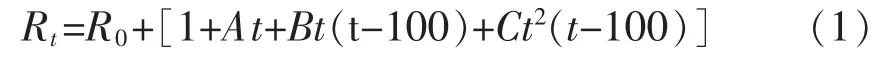
式中：Rt為溫度t時Cu電阻的電阻值；R0為t=0℃時Cu電阻的電阻值；A，B，C分別是對應的系數，A=4.28×10-3℃-1，B=-9.31×10-8℃-2，C=1.23×109℃-3。

本文將測出的數據分為（10℃～40℃）、（40℃～70℃）、（70℃～100℃）3個區間，然后利用最小二乘法對區間內數據進行一次、二次、三次、四次擬合，利用誤差評估原理得出Cu50熱電阻溫度傳感器的最佳校正方程。

2 基于Matlab的數據擬合方法

2.1 最小二乘法擬合原理

首先得到一組實測數據（xi，fi）（i=1，2，…，n），求出一個最佳擬合 y（x）∈φm=span｛φ0，φ1，…，φm｝，使得則 y（x）是在函數類 φm中的最小二乘逼近函數[8-9]。設y（x）=然后定義 m+1 元函數S（a0，a1，a2，…am），則有：

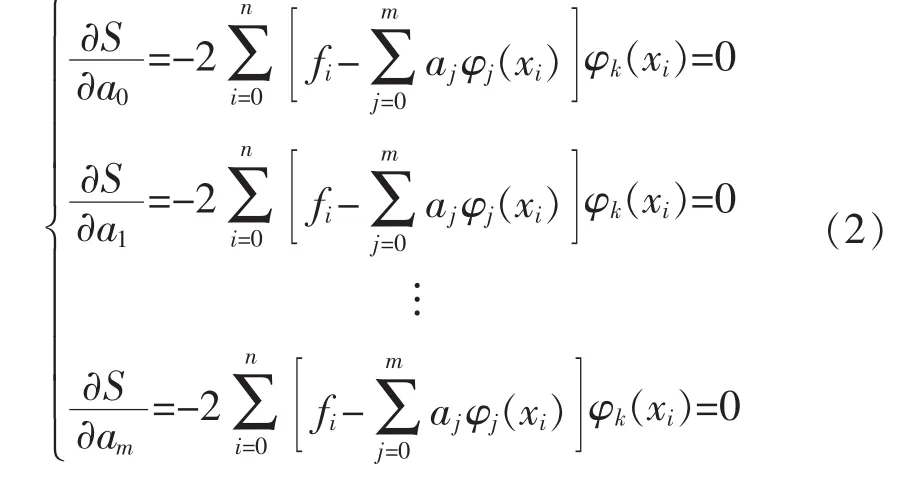
從而有：

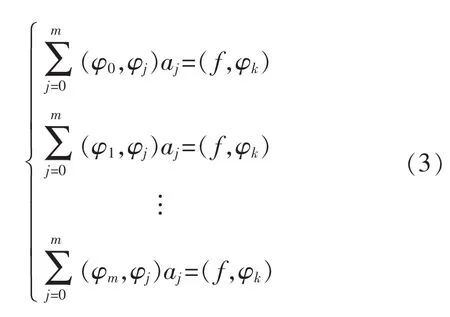
用矩陣形式表示為

求解方程即可得 a0，a1，a2，…，am。

2.2 基于Matlab的曲線擬合

Matlab中的內置函數polyfit可以進行n次多項式擬合[10-11]，其調用格式為

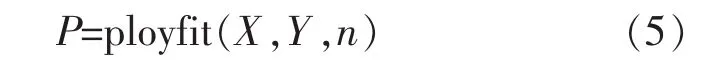
式中：X為試驗的溫度；Y為對應的電阻值；n為多項式的次數。

在（10℃～40℃）、（40℃～70℃）、（70℃～100℃）3個區間內分別進行一次、二次、三次擬合，擬合后的多項式系數如表1所示。

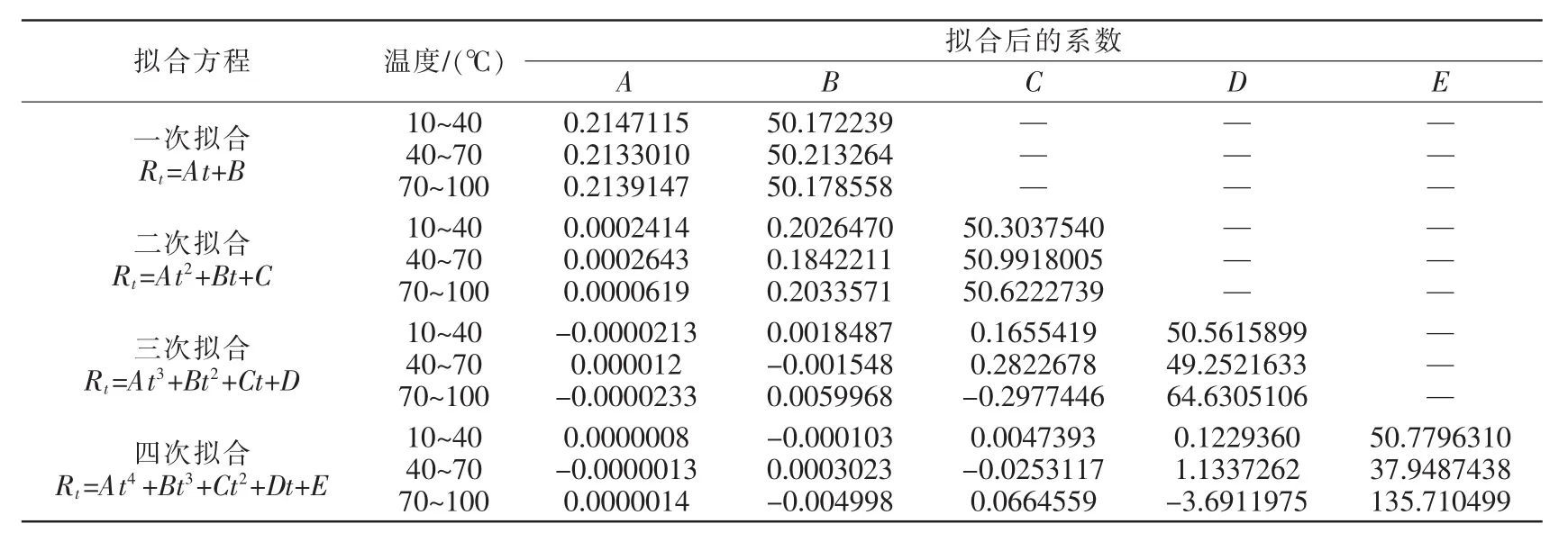
表1 Cu50溫度傳感器擬合多項式系數Tab.1 Cu50 thermal resistance temperature sensor’s quasi polynomial coefficient

利用最小二乘法分段擬合后的圖形如圖3所示。

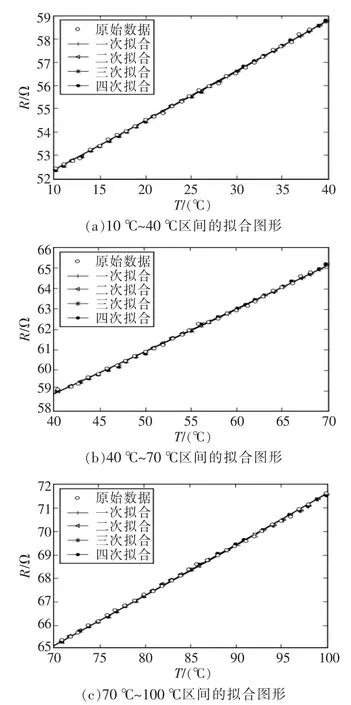
圖3 最小二乘法的分段擬合圖形Fig.3 Segmented fitting curve of least square method

2.3 擬合精度評估

為了評估校正方程的擬合精度，通常采用以下標準進行評估[12-13]：

（1）擬合殘差

式中：E（f）為校正方程的擬合殘差，E（f）越平穩，校正方程精度越高；yi為實測值；f（xi）為各擬合方程的擬合值。

（2）擬合偏差的最值

擬合偏差的最值就是擬合殘差的最值，它包括最大擬合偏差Emax（f）和最小擬合偏差Emin（f）。擬合偏差最值越小，選用的校正方程越理想。

（3）擬合殘差的算術平均值

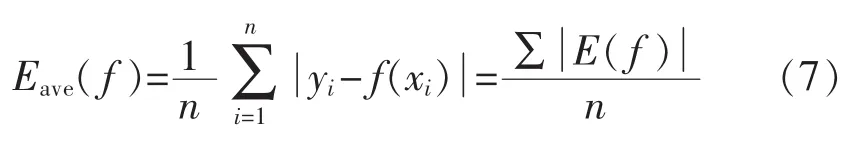
式中：Eave（f）為校正方程擬合殘差的算術平均值，Eave（f）越小，則校正方程精確度越高；n為實測數據點數。

（4）標準差

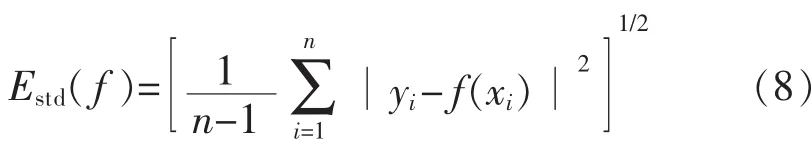
式中：Estd（ f）為校正方程標準差，Estd（ f）越小，校正方程精度越高。

2.4 擬合結果評估

由圖4可知在對Cu50溫度傳感器進行一次擬合時，擬合殘差波動很大，而對其進行二次、三次、四次擬合后，也不能通過擬合殘差評估出好壞，因此，通過3種擬合的擬合偏差的最值、擬合殘差的算術平均值及標準差進行對比，就可以得到Cu50熱電阻溫度傳感器的最佳校正方程，如表2所示。

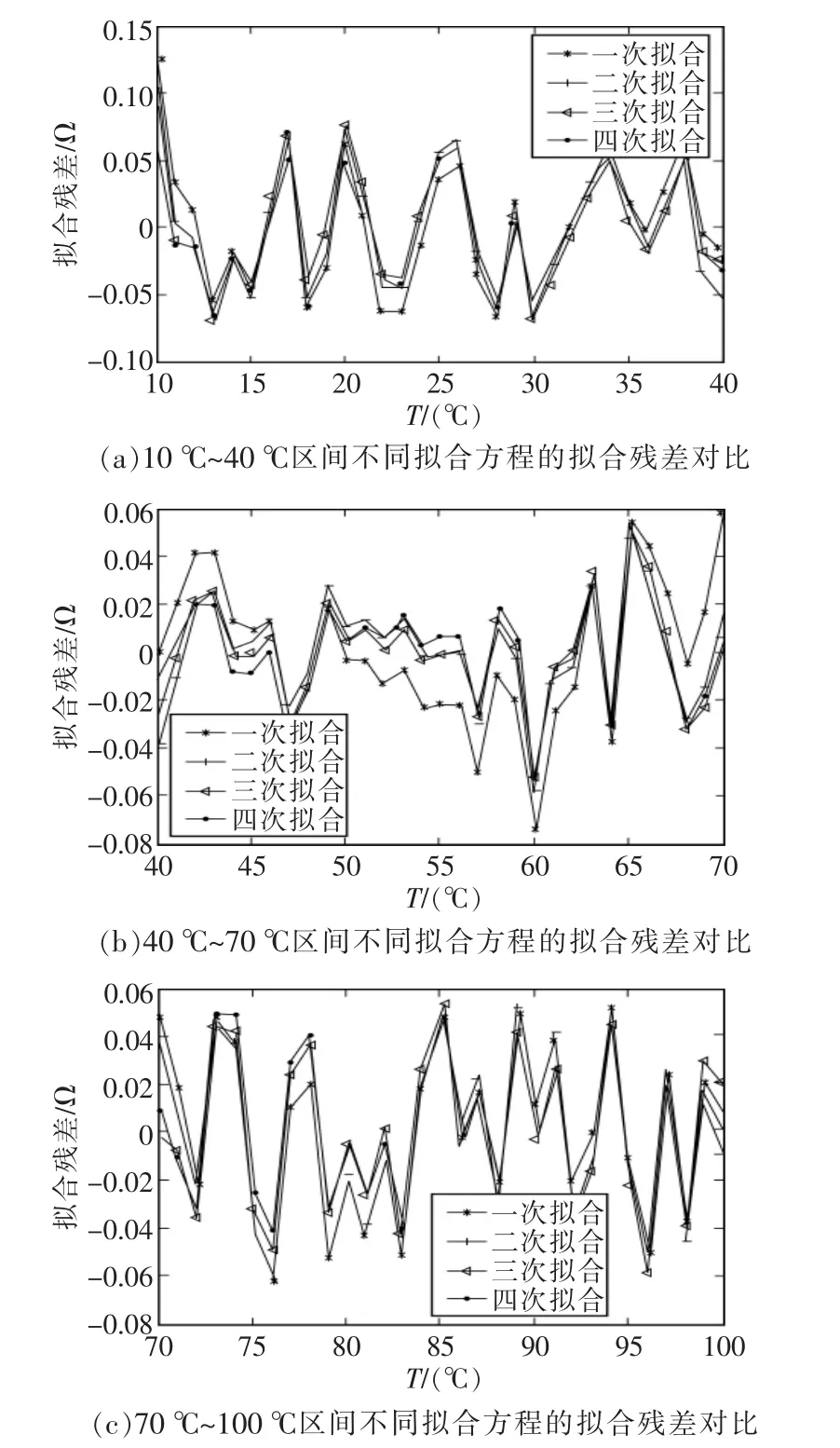
圖4 分段擬合的擬合殘差對比Fig.4 Comparison of fitting residual of the segmented fitting

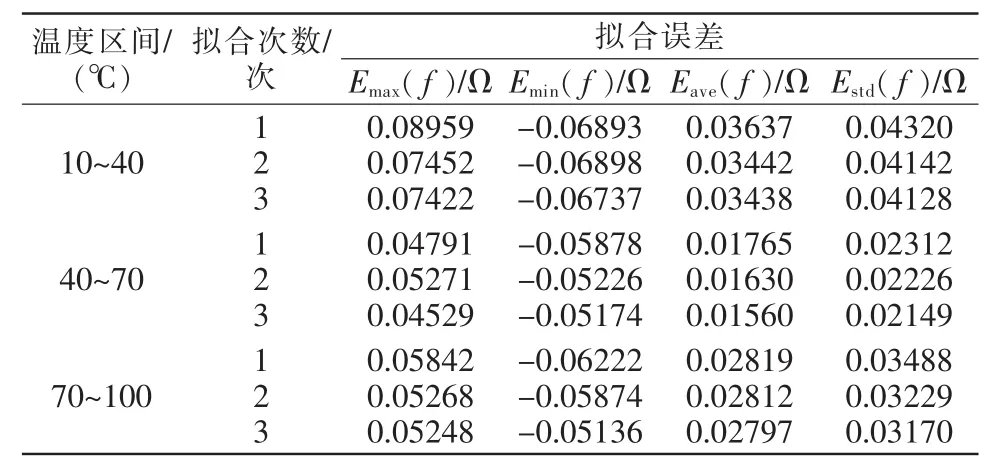
表2 Cu50溫度傳感器在10℃～100℃區間方程擬合誤差Tab.2 Equation fitting error of Cu50 temperature sensor at 10℃～100℃

由表2可知，在3個溫度區間內，四次擬合方程的最大偏差、最小偏差、擬合殘差的算數平均值、標準差為最小，由此可以得到，在10℃～100℃溫度范圍內，四次擬合方程是最適合Cu50溫度傳感器精度的校正方程，具體表示為

3 結語

本文采用最小二乘法對Cu50溫度傳感器的測量數據進行分段擬合，進而得到溫度與電阻之間的關系式，通過對絕對誤差，算術平均誤差以及標準誤差的綜合分析，得出在10～100℃溫度范圍內，與Cu50溫度傳感器T-R的實測數據的逼近度最高是四次擬合方程。通過驗證，四次擬合方程（9）比傳統方程（1）提高了2個數量級，在工業余熱吸收式制冷系統中得到了很好的應用。本文得出的校正擬合方法對于其他類的熱電阻溫度傳感器的校正擬合也很適用。

[1]劉天鍵，王劭伯，朱善安.基于神經網絡的鉑電阻溫度傳感器非線性校正方法[J].儀器儀表學報，2002，23（5）：81-84.

[2]李琴，劉海東.改進BP網絡及其在傳感器非線性校正中的應用[J].計算機應用與軟件，2009，26（7）：181-184.

[3]張修太，胡雪惠，翟亞芳，等.基于PT100的高精度溫度采集系統設計與試驗研究[J].傳感技術學報，2010，23（6）：813-815.

[4]張志勇，辛長宇，朱玉龍，等.Pt100溫度傳感器非線性的補償方法與電路實現[J].電子器件，2007，30（6）：2190-2191.

[5]田豐，孫小平，趙昱，等.基于BP神經網絡的濃度傳感器非線性校正[J].計算機工程與應用，2005，41（3）：226-228.

[6]林康紅，施惠昌，盧強，等.基于神經網絡的傳感器非線性誤差校正[J].傳感器技術，2002，21（2）：42-43，47.

[7]工業鉑.銅熱電阻JJG229-1998[S].北京：中國計量出版社，2004.

[8]陳嵐峰，楊靜瑜，崔崧，等.基于MATLAB的最小二乘曲線擬合仿真研究[J].計算機與現代化，2014，32（1）：75-78．

[9]楊大地，王開榮.數值分析[M].北京：科學出版社，2006.

[10]楊云升.Matlab曲線擬合及其在試驗數據處理中的應用[J].電腦與信息術，2009，17（2）：35-36.

[11]趙海濱.Matlab應用大全[M].北京：清華大學出版社，2012.

[12]張鵬超，張強.一種NTC熱敏電阻校正方程的試驗研究[J].傳感技術學報，2012，25（2）：221-223.

[13]錢政，王中宇，劉桂禮.測量誤差分析與數據處理[M].北京：北京航空航天大學出版社，2008.