EDXRF無標樣分析未知樣品含量的算法研究
白海濤,葛良全,張慶賢,劉永利,程 鋒,張 罡,趙 奎
(成都理工大學 核技術與自動化工程學院,四川 成都 610059)
能量色散X熒光分析(energy dispersive X-ray fluorescence analysis,EDXRFA)技術能夠快速、準確、經濟地對樣品進行多元素分析,分析精度在ug/g級別。該技術廣泛應用于工業分析、環境監測、地質礦產等領域[1]。但在EDXRFA分析中,儀器的無源效率刻度和基體校正一直是EDXRFA面臨的難題。近年來,針對EDXRFA無標樣刻度技術得到了深入研究。葛良全等[2]利用樣品歸類方法實現基本參數法在EDXRFA中的應用;劉敏等[3]進行了基本參數法在SDD-EDXRF無標樣分析技術中的應用研究,以及基本參數法無標樣校正釩-鈦-鐵間吸收增強效應[4]。樣品的質量衰減系數是基本參數法的必要參數,用于基本參數法的求解過程,而該參數與被測樣品的物質成分密切相關。從測量能譜中分析樣品基體信息求解質量衰減系數,是進行未知樣品無標樣分析的關鍵。2011年,傅卓人論證了未知樣品有效原子序數確定方法[5],用于確定未知樣的有效原子序數。EDXRFA在野外現場測量中,低原子序數元素(<18)難以準確分析,因此樣品存在未知成分。傳統算法并未考慮未知成分對含量解析的影響,并且用含有2~3種元素的樣品檢驗無標樣算法的準確性。本文針對未知基體地質樣品,研究能夠實現基體自動判別的X熒光無標樣定量分析算法,并通過測量分析15個國家的標準樣品,計算其Ti、Fe、Ni、Cu、Zn元素的含量,驗證算法的可靠性。
1 原理與方法
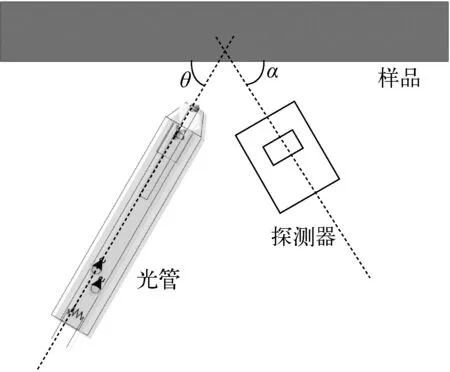
圖1 EDXRFA測量系統結構圖Fig.1 Measurement system structure figure of EDXRFA
能量色散X熒光分析(energy dispersive X-ray fluorescence analysis, EDXRFA)測量系統結構示于圖1,經光管發出的原級X熒光以θ角入射樣品,元素特征X射線和散射射線以α角進入探測器。假設樣品的厚度為無限厚,入射X射線的總強度為I0;探測器探測立體角為Ω,探測器對元素特征X射線本征探測效率為ε;對于元素的K層電子的吸收躍遷因子為Ji,Kα射線譜線分數為Fα,i,熒光產額為ωk,i;元素含量為Ci,對入射能量E的光電效應截面為τi,E。通過MCNP(a general Monte Carlo N-Particle transport code)模擬Rh靶的X射線原級譜線分布為ψ(E),分為102道;樣品對能量為E的X射線的質量衰減系數為μS,E,對i元素的Kα特征射線的質量衰減系數為μS,Kα。在以上條件下,i元素一次熒光強度可表示為[1]:
(1)
將式(1)改為式(2):
(2)
其中:
(3)
Hi=Ji·Fα,i·ωk,i
(4)
i元素二次熒光強度可表示為[1]:
(5)
其中:
(6)
Hj是j元素Kα特征射線的激發因子,由j元素吸收躍遷因子、譜線分數、熒光產額決定。
Gi是同儀器結構相關的參數,對一個固定的測量系統Gi是常數,可以由理論計算或者單標樣求解。通過以上公式,可以在已知參數條件下,求解熒光強度與元素含量的關系。
2 實驗方法
2.1 Gi參數確定
為了求解Gi參數值,首先制作了Ti、Fe、Ni、Cu、Zn、Sr、Sn、Pb等8個元素含量分別為0.1%、0.5%、1.0%、5.0%、10.0%的單物質標樣。分析精度為0.000 01 g的分析天平用于稱量,化學試劑為分析純。樣品由SiO2和H3BO3組成基體,研磨均勻。通過實驗室EDXRF熒光儀測量單元素標樣,利用公式(1)計算各元素的Gi值,計算結果列于表1。A-Gi表示元素的平均Gi值,R-E表示元素在不同比例下的Gi參數對于該元素A-Gi的相對誤差。
通過理論分析,當測量條件固定時,各元素的Gi為常數,表1中列出實驗結果與理論分析相符合,Ti、Fe元素相對誤差絕對值均在6%以內。因X射線光管的電壓為30 keV,光管對Sn、Pb元素激發效率低,計數統計漲落導致Sn、Pb元素的Gi參數波動較大。
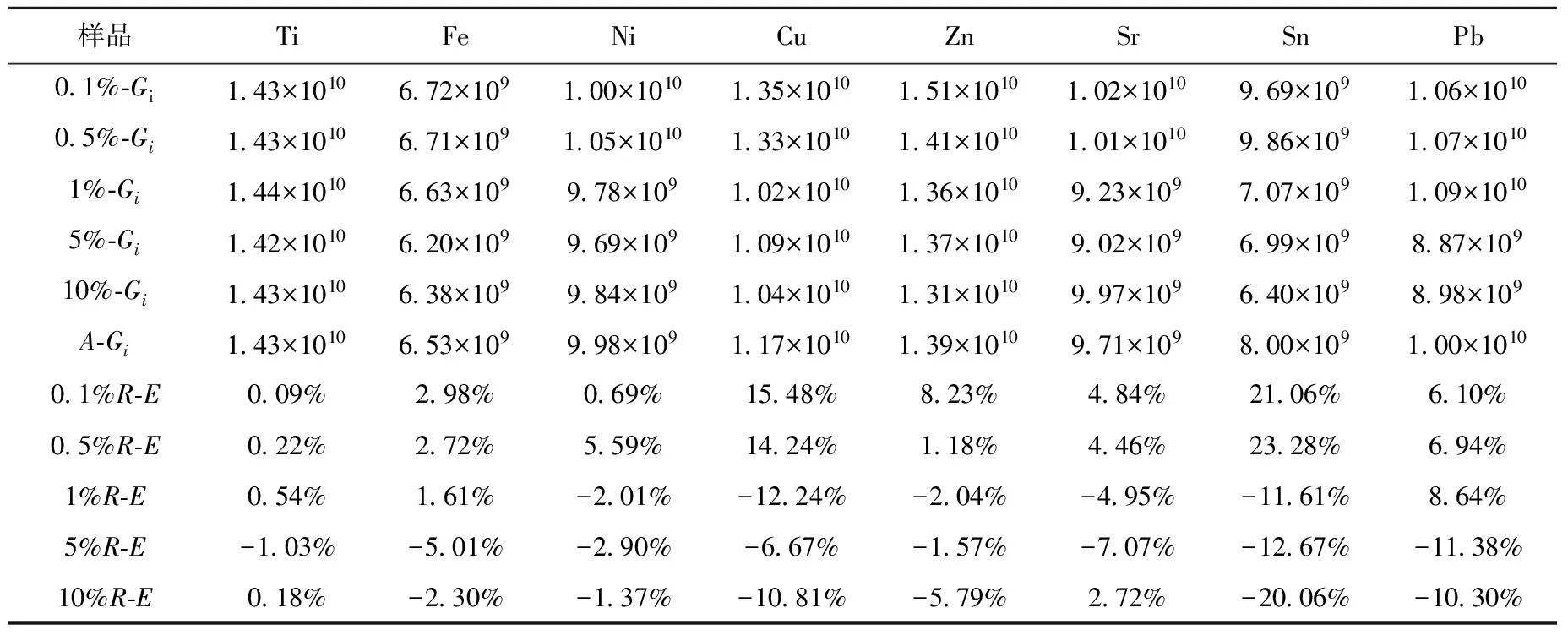
表1 各元素不同含量下的Gi值Table 1 The Gi value of each element in different content
2.2 基體確定
1) 根據Ti、Fe、Ni、Cu、Zn、Sr、Sn、Pb單元素標樣物質成分計算有效原子序數,計算公式如式(7)所示[6],其中Ci、Zi分別為單標樣中i元素的含量和原子序數。
(7)
2) 根據Rh靶原級譜線Kα峰的相干與非相干散射峰強度的比值R,得到Zeff-R的擬合曲線示于圖2。
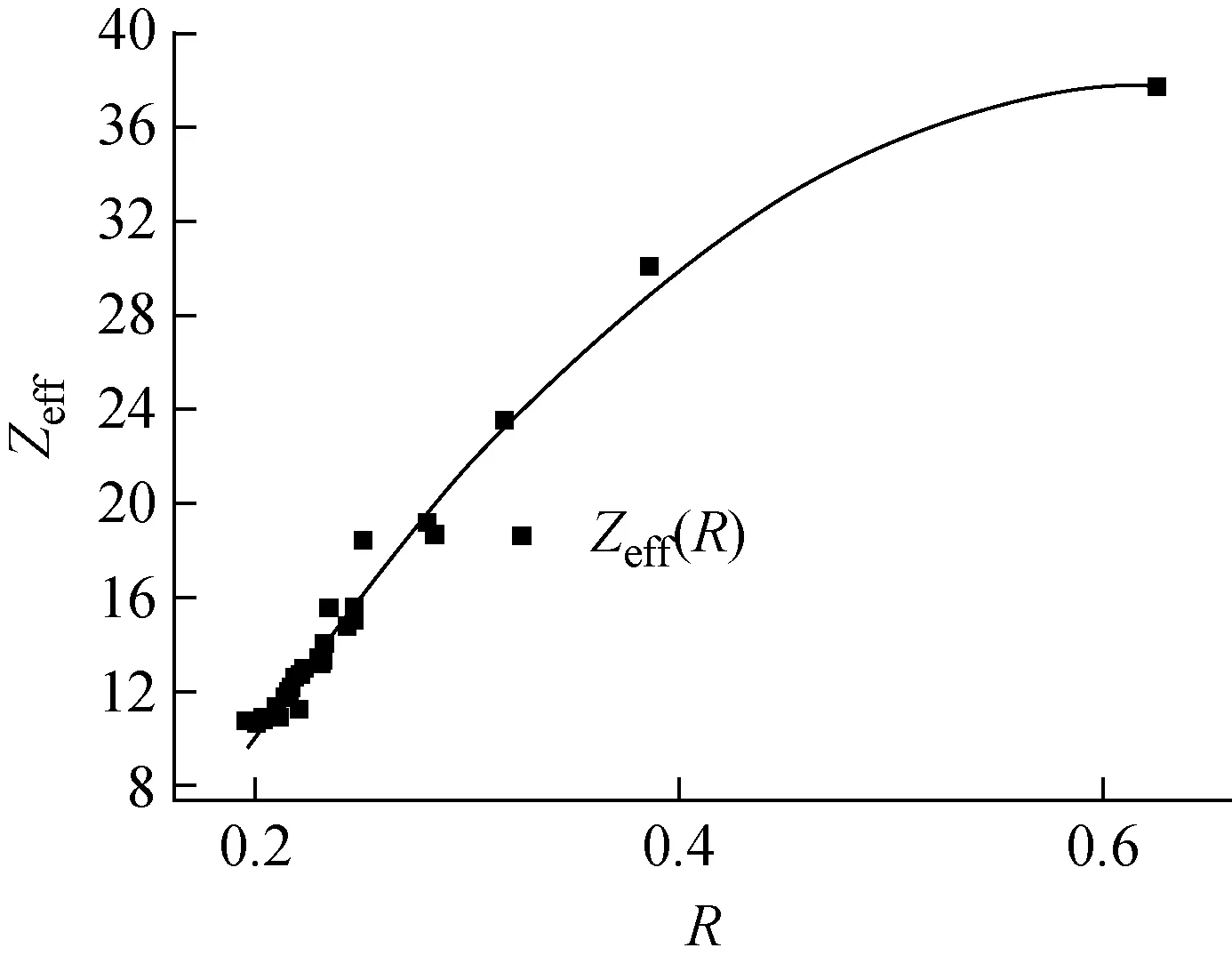
圖2 Zeff-R擬合曲線Fig.2 Zeff-R fitting curve
通過曲線擬合,得到Zeff-R擬合公式如下:
Zeff=-21.547 8+187.823x-148.215x2
(8)
擬合系數R2=0.984 2。
3) 初始迭代中,樣品基體的有效原子序數由式(8)求解,并根據有效原子序數計算樣品質量衰減系數,用于式(1)、(5)、(6)計算。
4) 由于有效原子序數未能準確表現元素的吸收限特征,改用下式表征樣品基體:
(9)
Zeff為根據公式(8)擬合得到的值,Ci是初步求得的含量,(1-∑Ci)是未知成分XZeff的含量。利用公式(9)求解未知成分的有效原子序數XZeff,從而求得μS,E、μS,Kα,求解公式如下:
μS,E=∑Ciμi,E+(1-∑Ci)uXZeff,E
(10)
μS,Kα=∑Ciμi,Kα+(1-∑Ci)uXZeff,Kα
(11)
2.3 基本參數迭代
基本參數迭代算法流程示于圖3,主要步驟如下。
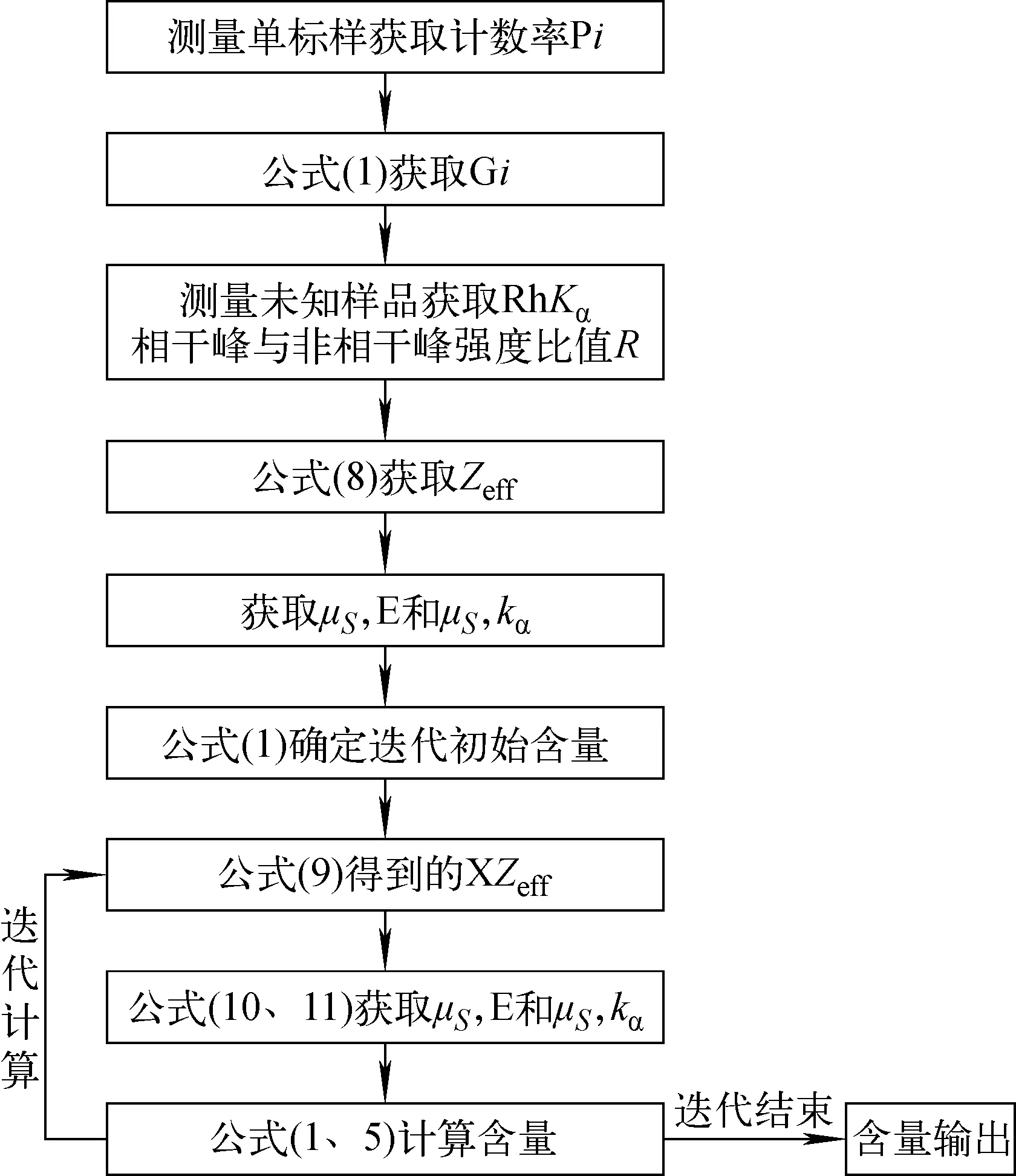
圖3 算法流程圖Fig.3 Algorithm flow chart
1) 由樣品測量能譜計算被測樣品原級譜線相干散射峰與非相干散射峰強度比值R,由公式(8)計算有效原子序數Zeff,通過Zeff獲得相應質量衰減系數。
2) 公式(1)中激發因子由參考文獻[7-8]中的數據求解,儀器參數Gi由2.1節求得。通過公式(1)確定待測元素的初始含量。
3) 將初始含量代入公式(9)計算樣品中未知成分的有效原子序數XZeff,再通過公式(10)、(11)得到相應質量衰減系數,并由公式(1)、(5)重新計算樣品中待測元素含量。
4) 重復步驟3,直到算法迭代收斂時,迭代結束,進行含量輸出。
3 結果與分析
利用本研究中的定量算法計算15個國家土壤標樣中Ti、Fe、Ni、Cu、Zn元素的含量,計算結果列于表2。由表2結果可見,Fe為百分含量,其他元素含量為μg/g,C-計算為本研究算法計算得到的含量,C-標準為國家土壤標樣提供的參考含量。R-E為C-計算與C-標準的相對誤差,如公式(12)所示;ν表示測量數據統計漲落的相對標準差,如公式(13),其中N為計數率;σ表示平均誤差,如公式(14)所示,其中n為樣品數。
(12)
(13)
(14)
由表2數據可見,Ti、Fe、Zn計算含量與標準含量接近,但不同元素的測量精度差異較大。
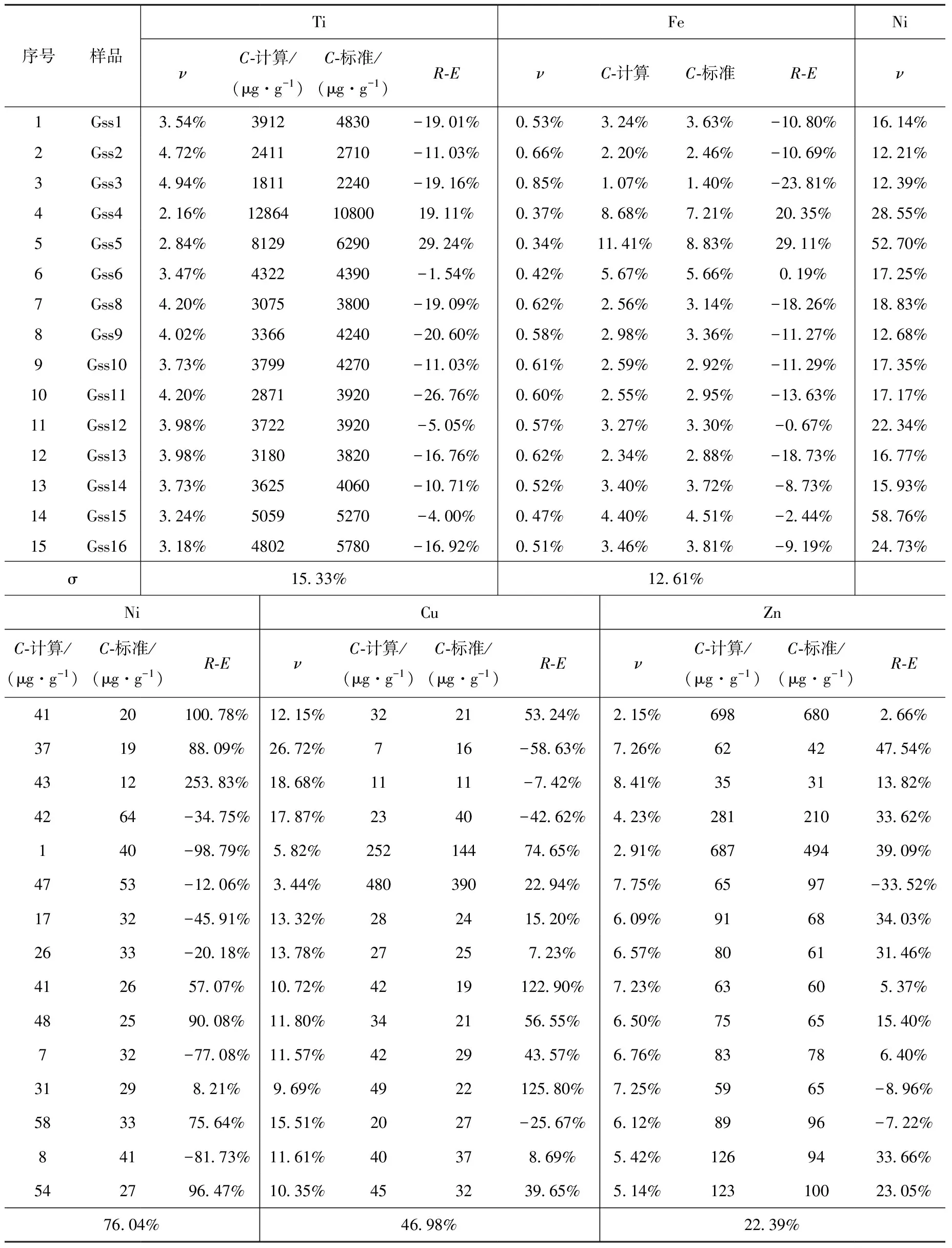
表2 樣品的標準含量和相對誤差Table 2 The standard content and the relative error of each samples
(1) 對于高含量元素,如Ti、Fe元素,含量在2 000 μg/g以上。Ti元素誤差最大為29.24%,最小為1.54%;Fe元素R-E最大為29.11%,最小為0.19%,并且Ti、Fe元素平均誤差均小于16%。誤差最大為Gss5樣品,其有效原子序數的計算因重元素光電效應導致偏離實際樣品值較大。Gss5樣品中重元素Pb含量達552 μg/g,而其他樣品小于100 μg/g。
對于Cu、Zn微量元素,其含量范圍11~680 μg/g,含量計算誤差與樣品含量相關。例如Cu元素誤差最大為125.8%時,其含量為22 μg/g,而Cu元素含量390 μg/g時,其誤差為22.94%。分析Zn元素也有類似結果。由于測量數據統計漲落、譜線解析等原因造成的誤差是測量誤差的主要來源。
(2) 對于Ni元素,標樣的Ni元素含量低,其Kα特征峰面積小,并且峰面積受Fe元素Kβ峰影響,測量數據離散度較大。將標樣中Ni元素標準含量和峰面積做線性擬合,結果示于圖4。由圖4結果可以看出,Ni元素的含量和峰面積已偏離線性關系,計算得到含量的誤差較大,偏離了實際含量。
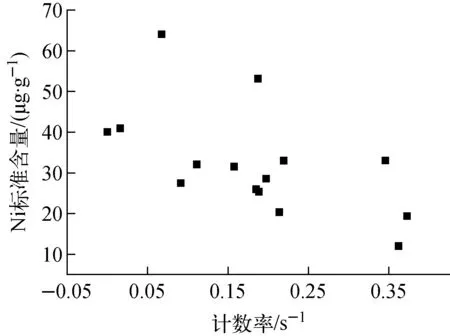
圖4 Ni元素標準含量和峰面積線性關系圖Fig.4 Linear relationship between the standard content and peak area of Ni element
4 結 論
針對未知基體的EDXRF分析,實現了自動基體分析的無源效率刻度方法,通過入射X射線的相干和非相干散射峰面積的比值R確定樣品的有效原子序數和質量衰減系數。采用單元素標樣測定了Gi參數。通過計算標準樣品中Ti、Fe、Ni、Cu、Zn元素含量驗證算法可靠性。結果表明,該算法能夠計算未知樣品的基體質量衰減系數和待測元素含量,能夠實現EDXRF的無標樣分析。但由于測量數據統計漲落、譜線解析帶來的誤差是EDXRFA誤差的重要源項,分析結果中部分元素相對誤差較大。因此在無標樣樣品分析中,需要進行精確的譜解析。
[1] 程鋒,張慶賢,葛良全,等. 能量色散X射線熒光分析中改進型基本參數法研究[J]. 光譜學與光譜分析,2015(7):2 034-2 037.
Cheng Feng, Zhang Qingxian, Ge Liangquan, et al. The study of advanced fundamental parameter method in EDXRFA[J]. Spectroscopy and Spectral Analysis, 2015(7): 2 034-2 037(in Chinese).
[2] 戴振麟,葛良全,鄒德慧. 能量色散X射線熒光分析基本參數法研究[J]. 核電子學與探測技術,2008,28(1):146-149.
Dai Zhenlin, Ge Liangquan, Zou Dehui. The research of fundamental parameters method in energy dispersive X-ray fluorescence analysis[J]. Nuclear Electronics and Detection Technology, 2008, 28(1): 146-149(in Chinese).
[3] 劉敏,庹先國,李哲,等. FP法在SDD-EDXRF無標樣分析技術中的應用研究[J]. 核電子學與探測技術,2012,32(9):1 096-1 099.
Liu min, Tuo Xianguo, Li Zhe, et al. The application of fundamental parameters method in EDXRF based on SDD[J]. Nuclear Electronics and Detection Technology, 2012, 32(9): 1 096-1 099(in Chinese).
[4] 劉敏,庹先國,李哲,等. SDD-EDXRF中FP法無標樣校正釩鈦鐵間吸收增強效應[J]. 核電子學與探測技術,2012,32(10):1 192-1 195.
Liu min, Tuo Xianguo, Li Zhe, et al. The calibration of vanadium titanium iron absorption enhancement effect in SDD-EDXRF[J]. Nuclear and Detection Technology, 2012, 32(10): 1 192-1 195(in Chinese).
[5] 傅卓人. 地質樣品中有效原子序數的確定[D]. 成都:成都理工大學,2011.
[6] 張偉軍. 化合物或混合物的有效原子序數研究[J]. 核電子學與探測技術,2013,33(1):120-126.
Zhang Weijun. A study on the effective atomic number of compounds and mixtures[J]. Nuclear Electronics and Detection Technology, 2013, 33(1): 120-126(in Chinese).
[7] 吉昂,卓尚軍,李國會. 能量色散X射線熒光光譜[M]. 北京:科學出版社,2011.
[8] 卓尚軍,吉昂. X射線熒光光譜分析[M]. 北京:科學出版社,2003.

