基于PSO小波神經網絡輔助卡爾曼濾波的BDS/INS定位

李衛東，黃晨陽，劉 楊，王新屏

(大連交通大學電氣信息學院，遼寧 大連 116023)

0 引言

在北斗定位系統(Beidou navigation satellite system，BDS)中，卡爾曼濾波是一種通過軟件消除定位信號噪聲的重要方法[1]。假如對列車運行模型構造不夠精確，會導致卡爾曼濾波后信號的發散、失真等不良結果[2]。通過構建卡爾曼濾波的輸入/輸出小波神經網絡，可以解決這些問題[3]。

本文結合文獻[1]～文獻[3]的優點，改進了小波神經網絡的學習率。在此基礎上，采用粒子群優化(particle swarm optimization，PSO)算法結合遺傳算法(genetic algorithm，GA)優化的小波神經網絡對實際問題進行建模。仿真試驗證明了該方法的有效性。

1 基于卡爾曼濾波的BDS/INS組合定位

目前，我國BDS總體性能略低于全球定位系統(global positioning system,GPS),它的主要問題可能在于:定位精度低、易受到無線電的干擾、保密性和安全性弱、 數據傳輸率低。這些缺陷可以通過與慣性導航系統(inertial navigation system，INS)結合來補償[4]。BDS/INS可以使北斗信號在由于遮擋或高強度干擾的情況下，能單獨進行導航定位，從而保證導航的可靠性。北斗系統可以修正INS的輸出信息，減少它隨時間積累的誤差，保證導航的精確性和工作的穩定性。

卡爾曼濾波是一種通過算法估計被提取信號的最優理論。自1980年以來，它被廣泛應用于運載體的導航和定位系統中[5]。

它的原理可以簡述為：假設Xk為tk時刻的被估計狀態，Wk-1系統的驅動噪聲序列驅動方程如下：

Xk=φk,k-1Xk-1+Γk-1Wk-1

(1)

對Xk的量測方程滿足線性關系：

Zk=HxXk+Vk

(2)

狀態一步預測：

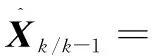
(3)

狀態估計：

(4)

濾波增益：

(5)

一步預測均方誤差：

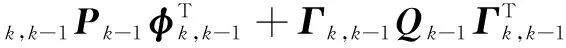
(6)

估計均方誤差：

Pk=(I-KkHk)Pk/k-1

(7)

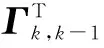
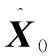
北斗定位系統與列車和地面設備時鐘一致，并向其上的接收機發送用于導航定位的調制波。導航電文發送隨機偽噪聲。理想情況下，接收機接收到電文后，將它與衛星信號的原電文進行對齊處理，求得衛星與接收機的距離和列車的相關參數[6]。INS器件通過測量移動載體的運動加速度及位移，再通過積分運算，推導出列車相關參數。隨后，BDS系統中的接收機將收到的相關列車參數，經電平轉換后，通過通信電路傳輸到信號處理器進行處理。同時在數字信號的裝置中將其中的慣性導航器件處理的信號導入，兩者信息相融合。

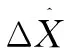
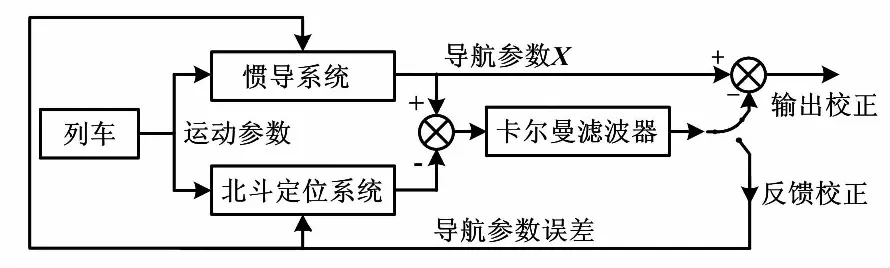
圖1 BDS/INS結構圖

2 小波神經網絡輔助的卡爾曼濾波

2.1 卡爾曼濾波的不足及彌補方法

實際運行中，由于列車運動模型不能準確構造以及系統中存在硬件誤差等原因，會導致經過卡爾曼濾波，獲得的速度波形與實際速度波形有偏差，進而使得到的定位信息也不準確[8]。雖然這些誤差的精確模型很難計算，但可以通過現有的卡爾曼濾波的輸入/輸出數據構造神經網絡模型，再對這個神經網絡模型進行校正。通過這種方式讓北斗定位系統獲取到較為準確的速度波形，從而提高北斗定位的精度。

采用圖2所示的神經網絡監督控制替換卡爾曼濾波。通過在線比較誤差的方法對小波神經網絡進行修正，逐步替換反饋控制器。在受到外界噪聲或其他因素干擾的情況下，控制器的反饋將會再次發揮作用。神經網絡監督控制方法，不但確保了控制系統能夠比較穩定地運行，還有效提高了系統的精度及其自適應的能力[9]。

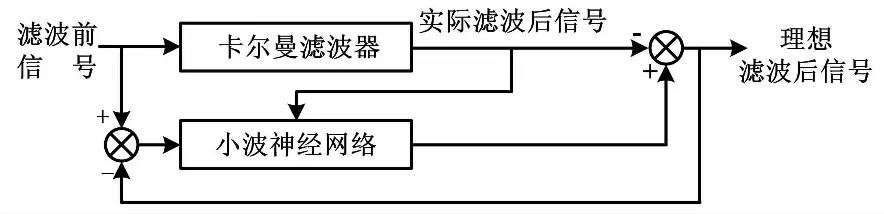
圖2 神經網絡監督控制圖

2.2 小波神經網絡結構

小波理論本身比較適合處理[10-11]小波神經網絡(wavelet neural network，WNN)。與神經網絡理論結合后，小波神經網絡算法具有更加靈活有效的函數逼近能力以及較強的容錯能力。其核心是將小波變換加入神經網絡模型中,構造以“Sigmoid函數”為基本構架的小波神經網絡。在構造小波神經網絡時，因為小波分解能夠進行平移，理論上能夠逼近任意函數。

本文根據信號的特點,采用了融合型的小波神經網絡。該網絡主體為3層網絡[12],具有單輸入、單輸出的結構，輸入層為并行輸入，隱含層、輸出層包含了m個神經元。

小波神經網絡結構如圖3所示小波函數中的伸縮，平移參數a、b和神經網絡參數都可以通過網絡學習進行訓練。圖3中，隱含層神經元的激勵函數f1是 Morlet 小波函數：

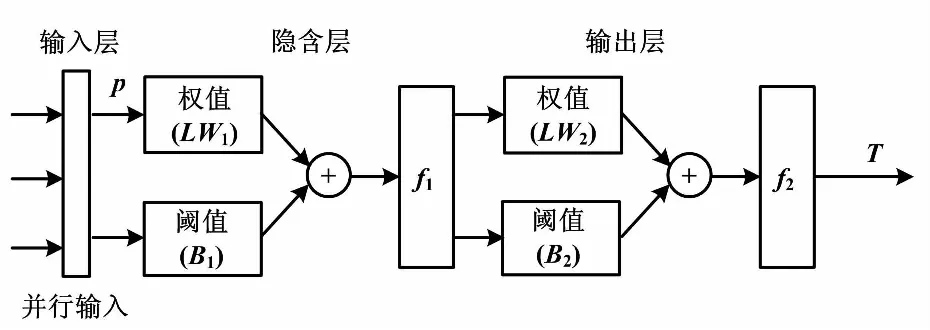
圖3 小波神經網絡結構圖

(8)

隱含層輸出為：

(9)

(10)

式中：O為隱含層的輸出；x為輸入層的輸入；w為權值；h為Morlet小波函數。

輸出層輸出為：

(11)

2.3 改進的小波神經網絡訓練算法

本文采用了改進的梯度下降法[13]，對小波神經網絡權值和參數進行訓練，誤差函數為：

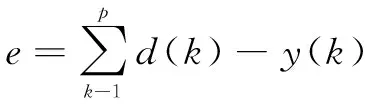
(12)

式中:d(k)為期望輸出；y(k)為網絡實際輸出；p為樣本數。

首先對輸入數據進行分割，并行輸入，得到權值平均值。這樣權值的反復變化次數減少，不但節省了時間，也提高了系統的穩定性。神經網絡主要基于誤差修正來進行結構的調整和學習,學習率的改變會影響收斂的速度和訓練的效果。如果學習率過小,系統的調節時間會太長;如果學習率太大,可能導致振蕩或發散。隨著時間增加，系統的調節幅度應相應減少。調整后的學習率單調增加且增加率逐漸變緩，log(a+x)無疑滿足這個條件。

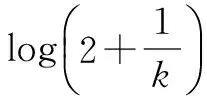
學習率的調整式：

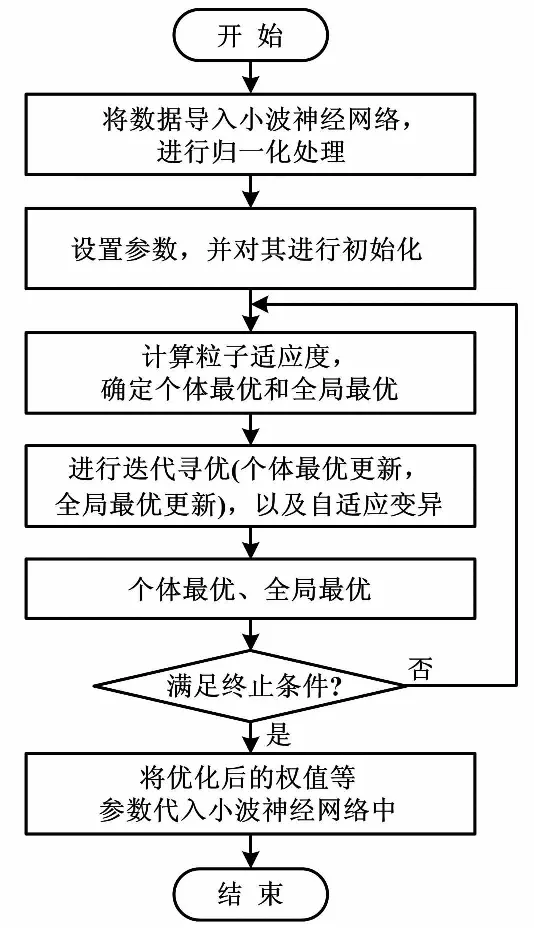
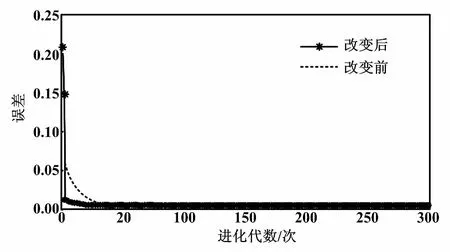
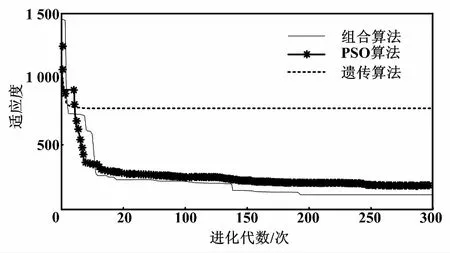
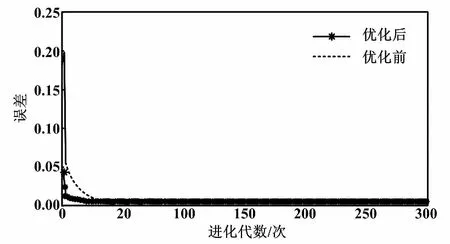
ηk+1=ηklog(1+k)e(k+1)

(13)

ηk+1=ηklog(2+1/k)e(k+1)≥e(k)

(14)

式中：η為學習因子；λ為動量因子。

改進的小波神經網絡訓練算法，一定程度上加快了小波神經網絡的收斂速度。但它仍然較易陷入局部最小，這無疑會對系統的收斂速度和精確度造成影響[13]。下面采用PSO與GA的組合算法來對小波神經網絡的權值和閾值進行修正，以進一步提升其性能。

3 粒子群優化算法優化的小波神經網絡

1995年，美國的Kenney和Eeberhart對鳥類的群體行為進行探究，提出了PSO算法[11]。每個粒子都可以看作潛在的要解決的優化問題的解決方案。粒子的速度取決于它的飛行的距離及其方向，它的適應值由優化函數決定。在飛行過程中，粒子經過多次迭代后，利用自身和飛行經驗組進行動態調整，最后取得最優解。粒子本身所得到的最佳值可以稱作個體的極值，而整個種群的最優解應是當前的極值。這一極值會在每個粒子尋找這兩個最佳值時更新：

vk+1=c0+vkc1(pbestk-xk)+c2(gbestk-xk)

(15)

xk+1=xk+vk+1

(16)

式中：vk為粒子的速度矢量；xk為目前粒子所在的位置；c0一般取介于(0，1)之間的隨機常數，通常可以稱為慣性系數或收縮因子。采用c1和c2的“自感知因子”和“社會認知因子”來調節pbestk和gbestk對粒子的影響。

GA的本質是構建一個針對優化問題的目標函數的適合度函數[12]。然后，根據一定的規則，生成遺傳密碼的初始組，并對該組進行評估，進行遺傳算法的交叉、變異、選擇等。

遺傳算法可以在不使算法變復雜的同時，提高算法的全局極值，從而提高算法的收斂速度和精度。在這種情況下，兩者優勢互補。它們的融合可以在提升學習速度的同時，增強系統的泛化能力。

PSO優化小波神經網絡流程如圖4所示。

圖4 PSO優化小波神經網絡流程圖

4 仿真分析

對所提算法進行仿真,試驗數據來自哈爾濱西至長春運營線路的實測數據，列車最高時速為200 km/h，平均車速為99.90 km/h[14]。設置北斗衛星接收機數據采樣頻率為1 s/次，哈爾濱西站的坐標作為初始位置的經緯度坐標，共收集了400個北斗Ⅱ衛星的測量數據(列車實際運行13.286 km)。為了便于分析，只采用了部分數據點進行仿真分析,并經由傳統的卡爾曼濾波獲得輸出波形及數據。

在試驗1中，小波神經網絡采用并行輸入[15]，輸入和輸出的節點數都為1，是3層神經網絡。其中隱層節點數為12，輸出層節點數為5。如果對數據分塊太多，則運行時間過長；如果數據分塊太少，則會使誤差偏大，所以將輸入數據分成了4塊。運行時間及均方差對比如表1所示。學習率改變前后誤差曲線如圖5所示。

表1 運行時間及均方差對比

圖5 學習率改變前后誤差曲線

在試驗2中，遺傳代數選擇了300代，種群規模選擇了50，變異率為0.95。算法適應度曲線如圖6所示。從圖6可以看出，組合算法在收斂速度上優于粒子群算法，且遠遠優于遺傳算法。

圖6 算法適應度曲線

在試驗3中，采用了北向的數據集，對基于GA改進的PSO權值部分進行訓練。當精度達到要求后結束訓練,進入在線狀態。在MATLAB 2015B中運行程序，對WNN輔助的卡爾曼濾波器所獲得的速度曲線和原來實際運行的曲線,以及它們的誤差曲線進行比較。優化前后誤差曲線、總體誤差對比曲線如圖7、圖8所示。

圖7 優化前后誤差對比曲線

從圖7、圖8可以看出，與實際運動曲線相比，經過改進的小波神經網絡輔助的卡爾曼濾波，對于速度的估計誤差更小,而且經過長時間的運行，偏差仍然不大,表明了通過小波神經網絡對卡爾曼濾波器輔助的方法是可行的。經過PSO優化后的神經網絡具有運行穩定且誤差小和收斂快等優點。在PSO優化數據后，相比優化前WNN 中100個輸出數據與理想輸出之差有所減少，整體的均方差也由原來的0.150 5降低到了0.019 4。

5 結束語

本文提出了一種采用WNN對實際問題中的卡爾曼濾波進行建模的方案。在此基礎上，對GA和PSO進行了組合優化。學習率則是通過加入對數函數進行改進。仿真表明，改進后的系統不僅加快了運行速度，而且減小了均方差。小波神經網絡優化不但提高了收斂速度,還有效提高了其定位的準確性，同時在保持原速度波形的整體趨勢前提下，減少了濾波導致的信號誤差。在今后工作中，考慮在BDS/INS慣性導航系統失效的情況下，利用神經網絡和其他算法融合進行運行路線的預測。

[1] 秦永元，張洪鉞，汪叔華.卡爾曼濾波與組合導航原理 [M].2版.西安：西北工業大學出版社，2012.

[2] 韓曉捷,陳德巧.基于神經網絡酌高速列車位置計算模型在線學習算法設計[D].北京：北京交通大學,2016.

[3] 周璐，郭超，鐘穎,等.小波網絡輔助卡爾曼濾波的捷聯慣導傳遞對準[J].計算機測量與控制,2015，24(32)：2518-2520.

[4] 張宇陽，蔡伯根.基于北斗/SINS融合的列車定位方法研究[D].北京：北京交通大學，2016.

[5] 羅建軍.組合導航原理及應用[M].西安：西北工業大學出版社，2012.

[6] 李笠,王萬良,徐新黎,等.基于網格排序的多目標粒子群優化算法[J],計算機研究與發展,2017，18(5)：1012-1023.

[7] 孟軍,史貫麗.融合粒子群優化和遺傳算法的基因調控網絡構建[J].計算機應用,2016，811(11):2969-2973.

[8] 徐澤遠,伊國興,魏振楠.MEMS - SINS / GPS 組合導航系統設計[J].自動化儀表,2016,37(12):67-70.

[9] 范廣坡,余學飛,盧廣文，等.改進PSO-BP算法的壓力導絲溫度及非線性補償研究[J].自動化儀表,2016，37(10)：12-16.

[10]周敏,劉健,楊林，等.一種自適應卡爾曼濾波在動態導航定位中的應用[J].自動化儀表,2016，37(8):1-4.

[11]黃杰，李軍，郭翔.遞推SOM神經網絡在短時交通流預測中的應用[J].自動化儀表,2015，36(4):1-5.

[12]HU Z T,YUAN G Y,HU Y M.Training method of neural network based on cubature kalman filter[J].Control and Decision,2016，31(2):355-360.

[13]SISWANTORO J,PRABUWONO A S,ABDULLAH A.Linear model based on kalman filter for improving neural network classification performance[J].Expert System with Application,2016,49(15):112-122.

[14]李衛東,賈洪明，馮祥雨.基于擴展卡爾曼濾波的列車定位[J].大連交通大學學報,2015(6):102-103.

[15]GU R H,BANERJEE A.Self-sensing SMA actuator using extended kalman filter and artificial neural network[J].Procedia,Engineering,2016，144(20):629-634.