基于壓縮傳感的小電流接地故障選線方法
張明磊,寧 媛,李 忠
(貴州大學電氣工程學院,貴州 貴陽 550025)
0 引言
隨著電力監測系統的快速發展,產生的大量信號會造成信號傳輸速度較慢、部分信號丟失以及硬件存儲空間不足等問題,影響硬件的高效運行。為此,應采取有效措施壓縮信號,以提高信號傳輸速度、減小存儲空間,使電力監測系統高效運行。
針對上述問題,提出了一種壓縮傳感方法[1-2]。該方法可以解決小電流接地故障選線中信號的采樣、傳輸和存儲問題。該方法與傳統信號采樣方法不同,它對信號的采樣是有選擇性的,在采樣過程中能夠減少大量的信號冗余。在采樣的同時進行壓縮,使采樣后得到的少量采樣點能通過重構算法很好地恢復原始信號。基于壓縮傳感理論的采樣能夠降低對硬件的要求,實現基于一般性能硬件的高效采樣。
信號重構算法的研究是壓縮傳感理論研究中的重要課題。目前有很多信號重構算法[3-5]。正交匹配追蹤算法[6](orthogonal matching pursuit,OMP)等能完成稀疏度已知的信號重構。在實際電力監測系統產生的信號中,信號的稀疏度一般是不確定的。因此,該算法就不能完成對信號的準確重構。對此,提出了交替乘子方向法(alternating direction method of multipliers,ADMM)[7-8]。該信號重構算法可以完成稀疏度不確定情況下的信號重構。
1 壓縮傳感原理
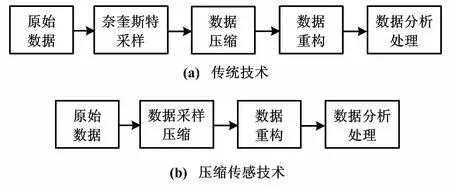
壓縮傳感理論,也稱為壓縮采樣理論、壓縮感知理論。該理論的采樣頻率不用考慮奈奎斯特采樣頻率。采樣信號是有選擇性的部分信號,并通過設計重構算法來準確恢復原始信號。該理論可描述為:如果一維信號XN×1在變換域ΨN×N中是K-稀疏的SN×1(K?N),則采用一個與變換域ΨN×N非相干的測量矩陣ΦM×N(M Y=ΦX=ΦΨS=ΘS (1) 式中:Θ=ΦΨ為傳感矩陣。 (2) 式中:‖S‖0為SN×1的L0范數。 信號的稀疏性,可以理解為信號XN×1在時域可能存在一個變換域ΨN×N,使得信號在該變換域中只有少數的非0元素,剩下的絕大多數元素為0或者較小值。其可表示為: X=ΨS (3) 式中:S僅有K(K?N)個不為0的值;X在變換域ΨN×N中具有K-稀疏性。 信號的稀疏性是應用壓縮傳感理論作為小電流接地系統故障選線的基礎,一般的信號通過一個稀疏基,即可達到稀疏性的效果。常用的稀疏矩陣有:快速傅里葉變換矩陣、離散小波變換矩陣[9]等。本文選取快速傅里葉變換矩陣作為稀疏矩陣。這也是目前應用廣泛的稀疏矩陣。 測量矩陣ΦM×N,用來對N維的XN×1進行測量得到YM×1。為了讓YM×1保留XN×1的主要特征,ΦM×N需要滿足約束等距特性準則(restricted isometry property,RIP)[1]。在這個特性中,存在一個常數δ∈(0,1),對任意XN×1都成立。 (4) 常用的測量矩陣有高斯隨機矩陣、稀疏隨機矩陣等。本文采用高斯隨機矩陣。 設高斯隨機矩陣ΦM×N,維數為M×N。N為待測信號的維數,M為測量維數,且M (5) 圖1 采樣壓縮流程對比圖 (6) 本文選取ADMM求解最小L1范數約束的重建問題,從而實現壓縮采樣信號的精確重構。 對于一個無約束的最優化問題,其目標函數為兩函數之和,且形式如下: (7) 式中:g為從Rn空間到Rd空間的映射。 若存在向量V∈Rd且滿足g(u)=v,則該問題可轉化為如下問題: (8) 下面采用ADMM求解式(8)。若設g(u)=gU,則有: 式中:G為變換矩陣,且G∈Rd×n。 對于如式(10)所示的有約束的最優化問題,其增廣拉格朗日函數定義為式(11): (10) 式中:A∈Rn×p、b∈Rp。 (11) 式中:λ、μ分別為拉格朗日乘子向量、懲罰項參數,且滿足λ∈Rp、μ≥0。 此式后兩項可以簡化為一個單獨的二次項: (12) (13) 那么: (14) 為了將式(9)化簡為式(10)的形式,則設: 且: E(z)=f1(u)+f2(v) (15) (uk+1,vk+1)∈argminu,vf1(u)+f2(v)+ (16) 交替乘子方向法求解式(16)的步驟如下。 ①初始化,設迭代次數k=0、μ>0,且選擇合適初值d0、v0。 ④利用式子dk+1=dk-Guk+1+vk+1更新d。 ⑤更新迭代次數,用k+1替代k。 ⑥判斷是否滿足迭代停止條件。若滿足,返回當前值uk、vk;否則,返回步驟②繼續執行。 交替乘子方向法的收斂性證明如下。 定理1 若存在如下有約束最優問題: (17) 式中:f1、f2均為凸函數;G為列滿秩矩陣,且G∈Rd×n。 (18) (19) ADMM產生的序列{uk}、{vk}和{dk}滿足定理1。由定理1可知,ADMM無需求解步驟②和步驟③。 本文采用 MATLAB/Simulink軟件,建立小電流接地系統單相接地故障時的動態仿真模型,驗證基于壓縮傳感的小電流接地故障選線的正確性和有效性。發電機端口引出三條線路并且末端分別接負荷,對其中一條線路設置單相接地。發電機采用中性點,經消弧線圈串聯電阻接地且端口接負荷。 模型參數如下。線路長度:L1=130 km,L2=175 km,L3=151 km。線路正序參數:r1=0.012 730 hms/km,L1=0.933 7 mH/km,C1=12.74 nF/km。線路零序參數:r0=0.386 40 hms/km,L0=4.126 4 mH/km,C0=7.721 nF/km。電源電壓:U=10.5 kV。采用過補償接地方式,補償度為10%。 稀疏矩陣采用快速傅里葉變換矩陣,測量矩陣采用高斯隨機矩陣,重構算法采用ADMM。選用的小波函數為db10。 設置系統總仿真時間為0.256 s,采樣時間為40 μs。系統在t=0.04 s時刻L3線路發生單相接地故障,故障點距離母線1 km,產生的信號大小為6 400點。 ADMM對測量信號進行重構,重構后的零序電流信號波形如圖2所示。在以上信號壓縮重構試驗中,原始信號大小為6 400點,經高斯隨機矩陣得到的測量信號大小為1 200點,壓縮比為5.3,重構誤差在5%以下,壓縮重構效果較好,為故障選線提供了良好的信號。 圖2 零序電流重構信號波形圖 采用小波函數db10對其進行分解,當分解到第7層時,其波形如圖3所示。由圖3可以看出,L3線路的零序電流模極大值的極性與L1、L2相反,認為L3線路為故障線路。 圖3 零序電流小波分解波形圖 (20) 采用小波對零序電流進行分解,可以獲取零序電流的主要特征。故障線路零序電流模極大值的極性與非故障線路相反[12]。根據這個極性相反來完成故障選線。 小電流接地系統單相接地故障時,經過壓縮重構后,采集得到三條出線零序電流。 為了解決小電流接地故障選線中信號的采樣、傳輸和存儲問題,本文將壓縮傳感理論應用到小電流接地故障選線中。基于壓縮傳感方法的采樣,不用考慮奈奎斯特采樣頻率的限制。采樣的信號是有選擇性的部分信號。通過設計重構算法來恢復原始信號,為下一步故障選線提供良好的信號。本文選取交替乘子方向法進行信號重構。從本文的仿真過程中可以看出,在信號稀疏度不確定的情況下,該算法重構信號的效果也較好,可以在實際工程中大量推廣。 壓縮傳感理論為解決海量數據采集、傳輸、存儲問題開拓了一條新的思路,可以應用于小電流接地故障選線,以及圖像采集、醫學成像、無線傳感器網絡和雷達成像等領域。由于其自身理論仍處于探索和研究階段,在特定領域應用方面也是剛起步,針對稀疏度不確定性等特定領域的重構算法將是今后研究的一個重要方向。 [1] DONOHO D L.Compressed sensing [J].IEEE Transactions on Information Theory,2006,52(4):1289-1306. [3] 王強,張培林,王懷光,等.機械振動信號分塊自適應壓縮感知算法[J].儀器儀表學報,2017,38(2):312-319. [4] 冷雪冬,王大鳴,巴斌,等.基于漸進添邊的準循環壓縮感知時延估計算法[J].物理學報,2017,66(9):77-84. [5] 劉靜,盛明星,宋大偉,等.基于分布式壓縮感知的聯合檢測與跟蹤算法[J].控制與決策,2017,32(2):239-246. [6] TROPP J,GILBERT A.Signal recovery from random measurements via orthogonal matching pursuit [J].Transactions on Information Theory,2007,53(12):4655-4666. [7] 李玉勝.交替方向法及其應用[D].合肥:中國科學技術大學,2015. [8] 鐘軼君.范數最優化問題的交替方向乘子算法[D].大連:大連理工大學,2013. [9] SUN Y B,XIAO L,WEI Z H.Sparse Representation of images by amulti-component gabor perception dictionary[J].Acta Automatica Sinica,2008,34(11):1379-1387. [10]DONOHO D L.For most large underdetermined systems of linear equations,the minimal L1 norm solution is also the sparsest solution[J].Communications on Pure and Applied Mathematics,2006,59(6):797-829. [11]DONOHO D L.For most large underdetermined systems of linear equations,the minimal L1 norm near-solution approximates the sparsest near-solution [J].Communications on Pure and Applied Mathematics,2006,59(7):907-934. [12]雷健新,張浩,彭道剛.配網電纜中性點小電阻接地故障及選線研究[J].自動化儀表,2016,37(9):48-51.1.1 稀疏性
1.2 測量矩陣
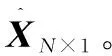
1.3 重構算法
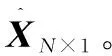
2 交替乘子方向法
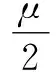
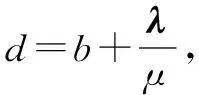
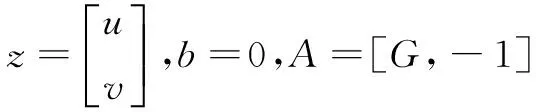
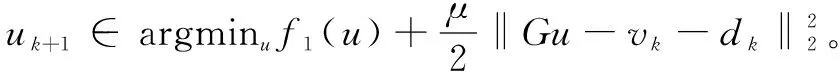
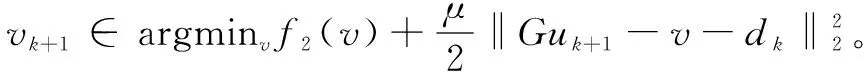

3 仿真試驗及分析
3.1 基于壓縮傳感的信號壓縮重構
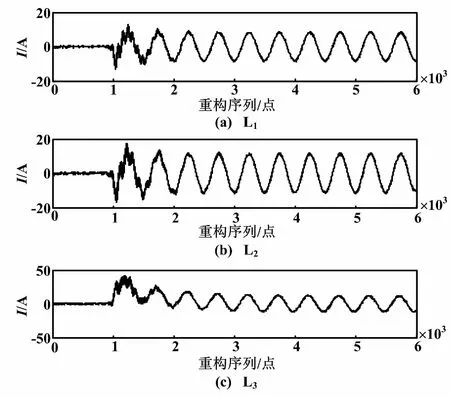
3.2 基于小波原理的故障選線
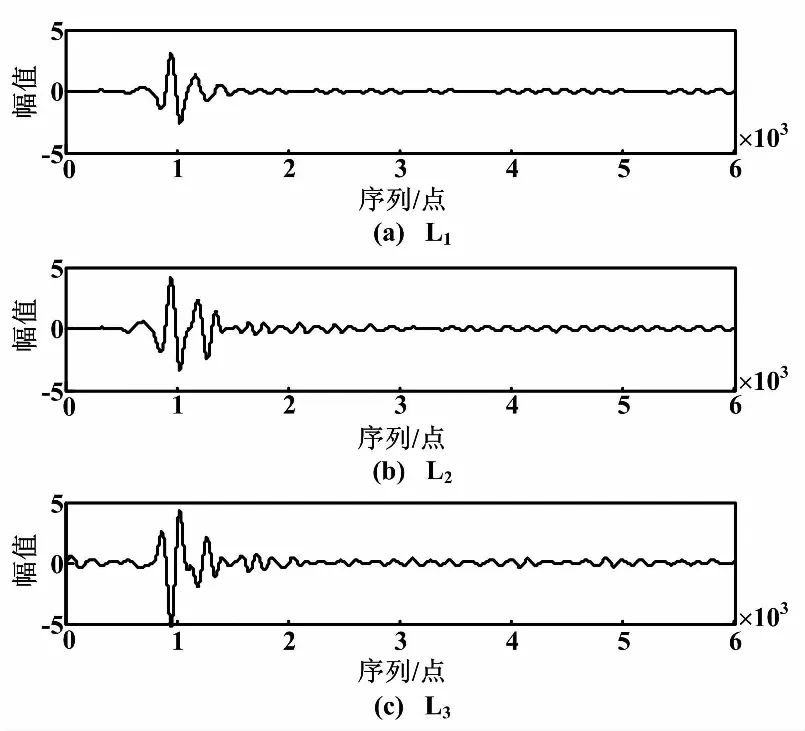
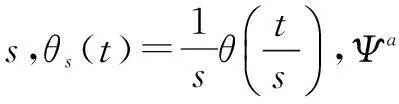
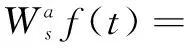
4 結束語

