基于改進FCM聚類醫學圖像配準
陳園+劉軍華+雷超陽

摘 要:ICP和互信息廣泛應用于醫學圖像配準,但存在以下問題:其計算量非常大,耗時長;受初始旋轉和平移參數影響較大,圖像配準容易造成目標函數陷入局部最優值。該方法通過計算參考圖像和浮動圖像的質心,獲得配準平移初始值;對醫學圖像坐標進行中心化處理,通過改進的FCM聚類方法把圖像坐標聚成2類;把這2個聚類中心擬合成一條直線,可以算出該直線的斜率,得出其傾斜角,從而獲得配準旋轉初始值。實驗結果表明,該方法既可用于單模態圖像配準,也可以用于多模態配準。還具有運算量少、圖像配準速度較快、計算比較簡單、精確度較高等特點,并且解決了圖像配準容易陷入局部最優的問題。
關鍵詞:圖像配準;fuzzy C-means聚類;迭代最近點;互信息
中圖分類號:TP391 文獻標志碼:A
Medical Image Registration Based on Improved Fuzzy C-means Clustering
CHEN Yuan,LIU Jun-hua,LEI Chao-yang
(Internet Engineering Department, Hunan Post and Telecommunication College, Changsha,Hunan 410015,China)
Abstract:The closest iterative point (ICP) algorithm and the mutual information (MI) technology, as intensity-based and feature-based medical image registration methods respectively, are commonly put into use in medical image registration.But some naturally existing things which restrict the further development need to be faced and be solved.On the one hand, they remain heavily calculation costs and low registration efficiencies.On the other hand, since they seriously depends on whether the initial rotation and translation registration parameters can be exactly extracted, they often traps in the local optimum and even fails to register images.In this paper, we compute the centroids of the reference and floating images by using the image moments to obtain the initial translation values, and use Improved Fuzzy C-means Clustering (FCM) to classify the image coordinates.Before clustering, this proposed method first centralizes the medical image coordinates, creates the two-row coordinate matrix to construct the 2-D sample set to be partitioned into two classes, and computes the slope of a straight line fitted to the two classes, finally derives the rotation angle from solving the arc tangent of the slope and obtains the initial rotation values.Obtains through the experiment,this proposed method can efficiently avoid trapping in the local optimum and is meet the single-mode and multi-mode state image registration.It has a low computational load,a fast registration,a fairly simple implementation and good registration accuracy.
Key words:image registration;FCM clustering;iterative closest points;mutual information
1 引 言
近年來,隨著醫學影像學的發展,CT、MRI、SPECT和PET等醫療設備的成像質量和圖像分辨率都有了很大提高,為臨床診斷和治療提供了可靠的依據。但由于各成像設備成像原理的不同,獲得的圖像信息也不相同,近年來對于各種醫學圖像配準技術的研究相當熱門。
醫學圖像配準技術是將CT、MRI、 PET、SPECT等一些醫學圖像通過計算機相關技術手段實現對于一幅醫學圖像尋求一種或者一系列的空間變換,使它與另一幅醫學圖像上的對應點達到空間上的一致[1-2]。近年來,該配準技術得到了專家學者們的高度關注并提出了了很多有效解決問題的方法。其中基于圖像特征和基于圖像灰度的配準方法[3-5]得到較為的廣泛應用,基于圖像特征的原理是通過查找圖像間共有的并有明顯特征的,從而獲取變換參數。采用該配準方法簡單且大大提高了計算效率。但由于醫學圖像的復雜性,圖像特征點的正確提取非常重要,采用該方法時計算機很難自動準確提取圖像特征點,需要我們人工輔助其選取圖像特征點,因此該配準方法在自適應性方面還需要進一步提高;基于圖像灰度配準的原理是采用互信息量[6-7]作為相似性測度,是直接對圖像配準且不需要對圖像做任何預處理的方法。但該方法計算量大且耗時長,圖像配準容易陷入局部極值從而導致配準失敗。endprint
為了解決以上問題,論文在仔細研究模糊C均值聚類(Fuzzy C-means Clustering)算法后,提出了基于改進FCM聚類醫學圖像配準(Medical Image Registration Using Improved Fuzzy C-Means Clustering,RIFCM)。該方法通過計算參考圖像和浮動圖像的質心,獲得配準平移初始值;對醫學圖像坐標進行中心化處理,得到兩行坐標矩陣,構成FCM的樣本集合,獲取初始聚類中心,把樣本集合聚成2類;把這2個聚類中心擬合成一條直線,可以算出該直線的斜率,從而得出其傾斜角,獲得配準旋轉初始值;把獲取的配準平移和旋轉初始值做為ICP和基于互信息的圖像配準初始值,并進行配準。該方法既可用于單模態圖像配準,也可以用于多模態配準。
2 基于改進FCM聚類醫學圖像配準
2.1 獲取圖像的質心坐標
對于二維離散函數f(x,y),它的(p+q)階矩定義為[8-9]:
Mp,q=∑Mx=1∑Ny=1xpyqf(x,y)p,q=0,1,2,…(1)
參數(p+q)稱為矩的階。
零階矩是物體的面積,其定義為[8-9]:
M0,0=∑Mx=1∑Ny=1f(x,y)(2)
所有的一階矩和高階矩除以M0,0后,與物體的大小無關。
當p=1,q=0和p=0,q=1時[8-9],
x-=M1,0M0,0,y-=M0,1M0,0(3)
則稱(x-,y-)為圖像中一個物體的質心坐標。
在配準時,f(x,y)表示在點(x,y)的灰度值,根據(1)-(3)式分別計算參考圖像R和浮動圖像F的零階矩和一階矩,得到各自的質心坐標(xR,yR)和(xF,yF)。
2.2 使用改進的FCM獲取圖像的傾斜角
Bezdek在1973年提出了模糊C-均值聚類(FCM)[10-11],即模糊ISODATA,目前已成為非監督模式識別的一個重要分支。在近20-30年內FCM聚類方法在圖像處理中得到了較為的廣泛應用,其中在醫學圖像處理領域也取得了較好得效果。如Lee等人[12] 利用FCM算法糾正T1加權圖像中的偏差;Pham等人[13] 通過自適應FCM算法分割強度不均勻圖像;Udupa等人[14]利用FCM算法中的模糊連接度理論解決了三維空間中不同體素連接的緊密程度;王海波等人[15] 利用兩次FCM算法完成出血區域分割。
2.2.1 FCM聚類算法
對于模糊C-均值聚類(FCM)算法,我們設X={x1,x2,…,xn}由n個樣本組成的集合且xi=[xi,1,xi,2,…,xi,k]T,i=1,2,…,n,c是給定的聚類數,vj(j=1,2,…,c}是每個聚類的中心,且有vj=[vj,1,vj,2,…,vj,k]T,j=1,2,…,c,μj(xi)表示第i個樣本第j類的隸屬度,且設∑cj=1μj(xi)=1, i=1,2,…,n。將聚類目標函數可定義為:
J(U,V)=∑cj=1∑ni=1[μj(xi)]l‖xi-vj‖2(3)
其中U代表X的模糊C-劃分,V代表聚類中心集合,l代表模糊加權冪指數,選擇‖xi-vj‖代表樣本xi與聚類中心vj間的歐氏距離。通過FCM聚類獲得使目標函數達到最小時的U和V,令J(U,V)對vj和μj(xi)偏導數為0,即J(U,V)vj=0和J(U,V)μj(xi)=0,則有:
vj=∑ni=1[μj(xi)]lxi∑ni=1[μj(xi)]l,j=1,2,,…,c(4)
μj(xi)=(1/‖xi-vj‖2)(l-1)-1∑ck=1(1/‖xi-vk‖2)(l-1)-1,i=1,2,,…,n;j=1,2,…,c(5)
由此得到,FCM聚類過程具體描述如下[16-17]:
步驟1.設初始化為U,迭代次數T=1,允許最大迭代次數為Tmax,聚類數目為c和參數為l, ε代表算法終止閾值;
步驟2.由(5)式得,隸屬函數為μj(xi);
步驟3.由(4)式得,通過當前的隸屬函數更新各類聚類中心;
步驟4.當條件滿足時,返回步驟2,直到‖V(T+1)+V(T)‖≤ε or T≥Tmax,算法迭代則結束。
從上述算法過程描述中得到,FCM聚類算法我們要先設定初始聚類中心U和聚類數c,為了有效縮短算法收斂時間,我們需要設置較好的初始聚類中心。
2.2.2 FCM聚類算法選擇初始聚類中心
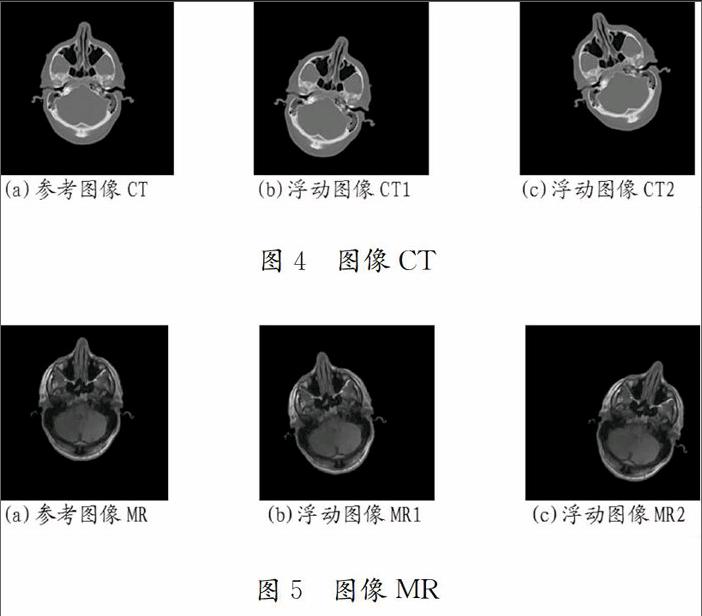
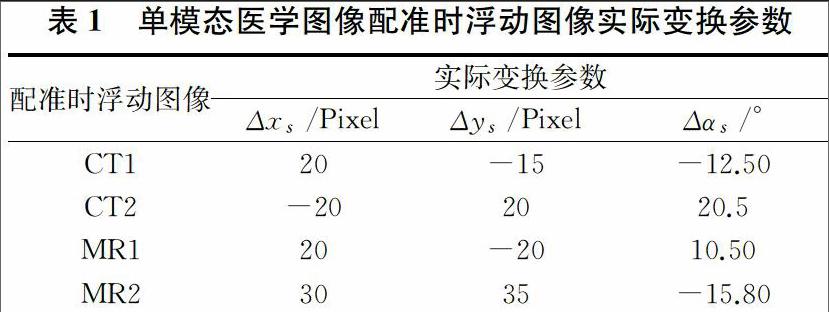
在實驗時,我們首先要來討論FCM聚類的運行時間、允許的最大迭代次數Tmax與獲取的傾斜角等它們之間的關系。由于初始聚類中心的選擇直接影響聚類結果,且FCM聚類對初始聚類中心比較敏感。在圖1(a)、(b)兩幅傾斜醫學圖像中,當隨機選擇初始聚類中心時,得到如圖2(a)和圖2(b)所示的Tmax與獲取的傾斜角的關系、Tmax和FCM聚類運行時間的關系。
對于圖1(a),通過FCM聚類后,得到圖2(a)所示,在Tmax還是較小值時,得到的傾斜角不夠穩定,在Tmax≥40后傾斜角趨于基本穩定;對于圖1(b),在Tmax還是較小值時,傾斜角在一定范圍內震蕩,處于不穩定狀態,在60≤Tmax≤260時傾斜角基本上在兩個角度之間不斷切換,這種聚類的結果不可預測,在Tmax>260時傾斜角基本趨于穩定,但是迭代次數較大。從圖2(b)可以看出,當Tmax=270時FCM聚類算法運行時間出現一個極小值,但從整體來看兩幅圖像的Tmax與運行時間基本上成線性上升,在Tmax>260時負傾斜圖像傾斜角才趨于穩定,且運行時間較長。所以在聚類時一定要選擇適當的初始聚類中心或者初始隸屬度函數。endprint

