多元函數條件極值的一種較精確的充分條件

張 馳，胡 博，秦 琴，鐘海全

（1.廣東省華立技師學院建筑與經濟學部，廣州 511300；2.卡斯柯信號有限公司平臺軟件部，上海 200071；3.廣州大學松田學院，廣州 511370；4.西南石油大學油氣藏地質與開發工程國家重點實驗室，成都 610500）

對于無條件極值問題，應采用目標函數的Hesse矩陣作為判別其充分條件的依據，許多教材都有詳細的闡述；但對于用拉格朗日乘數法解多元函數條件極值時充分條件的判別矩陣，因其比Hesse矩陣復雜許多，少有教材〔1-3〕詳細論述。兩種充分條件的判別矩陣具有差別的原因在于：條件極值問題帶有等式約束，其駐點處的自變量增量不全為獨立變量，即自變量增量間存在約束關系；而無條件極值的自變量增量之間沒有約束關系，因而可直接采用Hesse矩陣判定。所以要尋找精確的條件極值的充分條件的判別矩陣，就應求出自變量增量中非獨立變量關于獨立變量的解析表達式或數值表達式。本文分析了兩種充分條件的關聯及差別，詳細推導了條件極值的充分條件的判別方法；在滿足隱函數存在定理的條件下，于駐點處對約束條件作一階泰勒展開，進而求出非獨立變量關于獨立變量的解析表達式。本文有助于理解無條件極值和條件極值的充分條件的關聯及差別，在此理解上，給出了一種尋找更精確的條件極值的充分條件的判別矩陣的方法。

1 無條件極值充分條件的判別法與條件極值充分條件的判別矩陣

為方便與后文中條件極值的充分條件的判別法作對比，此處先回顧無條件極值的充分條件。設R為實數域，n維歐幾里得空間為Rn，即Rn={(x1,x2,…,xn)|x1,x2,…,xn∈R1}，則Rn具有實線性空間的代數結 構 和 距 離 結 構 ：?x=(x1,x2,…,xn)，y=(y1,y2,…,yn)∈Rn，λ∈R1，有x+y=(x1+y1,x2+y2,…,xn+yn)，λx=(λx1,λx2,…,λxn)，歐氏距離

設目標函數f(x)是定義在Rn中區域Ω上的函數，X0=()是Ω的內點，f(x)在X0的一個鄰域內具有二階連續偏導數，且X0是f(x)的駐點，即?f(X0)=0；記Hn為f(x)在X0的Hesse矩陣，則有：若Hn正定，則X0是f(x)的極小值點；若Hn負定，則X0是f(x)的極大值點；若Hn的特征值有正有負，則X0是f(x)的鞍點；其余情況，則不能判定X0的狀態。

對于求解等式約束條件極值的問題，可轉化為求解無條件極值，即拉格朗日乘數法，便可應用求解無條件極值的方法得到駐點，這實際上是一種降維思想〔4〕。雖然乘數法解出的是拉格朗日函數的駐點，但因為可行域內的點均滿足等式約束，所以拉格朗日函數的駐點也是f(x)的駐點。

現設n,m∈N+，m＜n，且本文中的f(x)在定義域內對每個自變量xi具有二階連續偏導數，等式約束有m個：

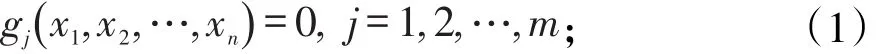
在駐點及其某一鄰域內滿足條件Jacobi矩陣行滿秩，即式（2），以及滿足式（3）

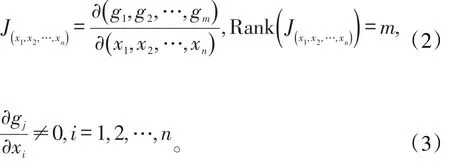
作Lagrange函數：

解這n+m個方程可得駐點。在任一駐點處，顯然滿足m個等式約束，即；又因為是條件極值問題，所以任一駐點處的任一改變量均應在可行域內，則該駐點處的微小改變量也應滿足這m個等式約束，即，則有，則該駐點X0為極小值點；若，則X0為極大值點；若Δf()X有正有負，則X0為鞍點。

對L函數（4）在駐點X0作關于的二階泰勒展開，此時需將L函數中的看作常量，可得：

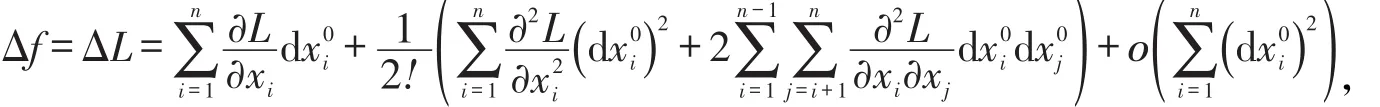
由條件極值的必要性條件〔1，5〕可得：

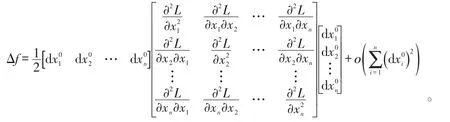
此時Hesse矩陣若仍采用無條件極值的充分條件〔1〕判別，則有：若在該駐點X0處Hn正定，則該駐點為極小值點；若Hn負定，則X0為極大值點；若Hn的特征值有正有負，則X0為鞍點；其余情況，則不能判定X0的狀態。無條件極值的充分條件判別法是將n個dx0i均作為獨立變量，但對于條件極值，由于存在m個等式約束，則獨立變量其實只有n-m個，另外m個變量為這n-m個獨立變量的隱函數〔6〕，即為非獨立變量，所以需求出非獨立變量關于獨立變量的表達式才能更精確地判別極值，這是條件極值充分條件判別法與無條件極值充分條件判別法不同的關鍵。

現在繼續討論條件極值的充分條件的判別方法。對等式約束（1）在滿足式（2）及式（3）（即滿足隱函數存在定理〔7〕）的駐點X0處作一階泰勒展開，可得：

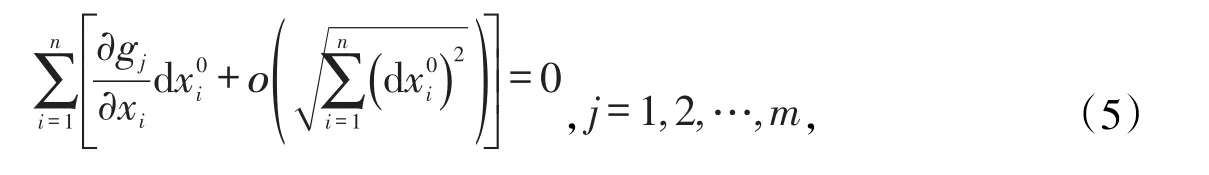
當dxi0足夠小，假設，于是解這m個線性方程可得：此時是將作為獨立變量，其中記系數矩陣Am×()n-m為：

記單位矩陣In-m為：

記Hesse變形矩陣H?n-m為：

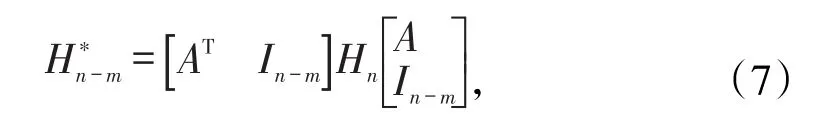
在駐點X0處，當足夠小時是二次型的高階無窮小，則Δf與同號〔8〕；此時若正定的特征值全為正，則所有二次型取極小值，該駐點X0為極小值點；若負定，的特征值全為負，則所有二次型取極大值，X0為極大值點〔9-10〕；若的特征值有正有負，則二次型有正有負，Δf(X)有正有負，X0為鞍點；其余情況，則不能判定X0的狀態。

2 條件極值的充分條件的判別矩陣中系數ajk的確定

既然無條件極值采用的判別矩陣Hn與條件極值采用的判別矩陣有所差別，則需求出中系數矩陣Am×(n-m)，即找到ajk的表達式，才能更精確地判別極值。

當n=3,m=2時，目標函數為：f(x1,x2,x3)，等式約束（1）變為式（8），

且L函數（4）在駐點X0處均滿足式（2）及式（3）。設此時Jacobi行列式為即以x3作為獨立變量，此時i=1,2,3;j=1,2，則對等式約束（8）在駐點處作一階泰勒展開可得

當n=4,m=2時，目標函數為：f( )x1,x2,x3,x4，等式約束（1）變為式（9），

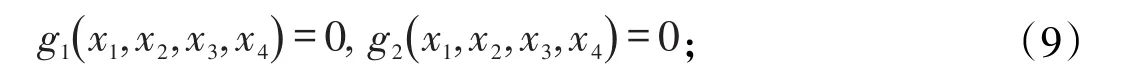
且L函數（4）在駐點X0處均滿足式（2）及式（3）。此時設Jacobi行列式為即以x3,x4作為獨立變量，此時i=1,2,3,4;j=1,2，則對等式約束（9）在駐點處作一階泰勒展開可得：

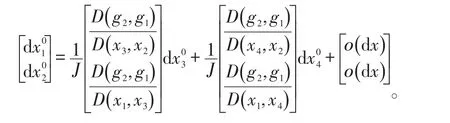
繼續求解高維多約束的情形，并由數學歸納法可推知，?n,m∈N+,m＜n，k=1,2,…n-m，當目標函數為f(x)，等式約束為（1），且L函數（4）在駐點處均滿足式（2）及式（3）時，則對等式約束（1）在駐點處作一階泰勒展開可得如下關系式：

當j=1，即求系數矩陣Am×(n-m)的第一行系數a1k時

例如：

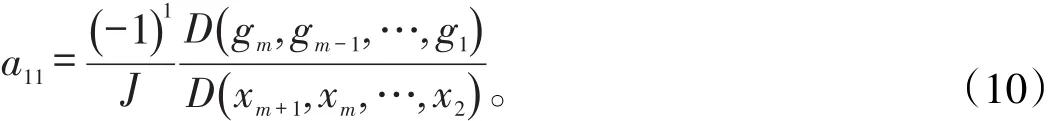
當j=m，即求系數矩陣Am×(n-m)的最后一行系數amk時

例如：

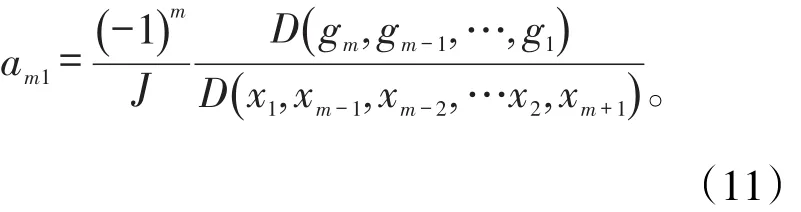
當j=2,3,…m-1，即求系數矩陣Am×(n-m)的中間行系數ajk時，

例如，當j=2，即求系數矩陣Am×(n-m)的第2行系數a2k時

系數ajk中分母部分乘積右側各元素的變化規律為：x共有m個元素：x1,x2,…,xm，其中xj不存在，被xm+k在第j列取代，其余的元素從xm,xm-1,…,xj+3,xj+2,x1依次排列在xm+k右側，xj+1,xj-1,xj-2,…,x2依次排列在xm+k左側。需要注意的是，若ajk中各元素排列順序發生變化，則ajk的正負符號可能發生變化：當變動奇數次時，符號改變；當變動偶數次時，符號不變；其中變動次數指各元素按相鄰順序依次變動的次數。

3 應用舉例：采用Hn與判別條件極值的差別

此處應用與文獻〔6〕中相似的例子來驗證條件極值的充分條件應采用Hn?-m而不是Hn來判別極值。設笛卡爾坐標系中有橢圓方程，

求該橢圓上的點到坐標原點距離的極大值和極小值。由題可知，式（12）是以坐標原點為頂點，y軸為轉軸的旋轉拋物面；式（13）是過（1，0，0），（0，1，0），（0，0，1）三點并以（1，1，1）為一法向的平面；二者交線為一橢圓，其上點到原點的距離必存在極大值和極小值。或者可采用文獻〔6〕中初等數學的方法證明極大值和極小值的存在。

解：原題等價于求目標函數f(x,y,z)=x2+y2+z2在等式約束g1(x,y,z)=y-x2-z2=0，g2(x,y,z)=x+y+z-1=0下的極大值和極小值。作L函數L(x,y,z,λ1,λ2)=f+λ1g1+λ2g2，由條件極值的必要性條件〔5，7〕可得L函數的兩個駐點分別為：

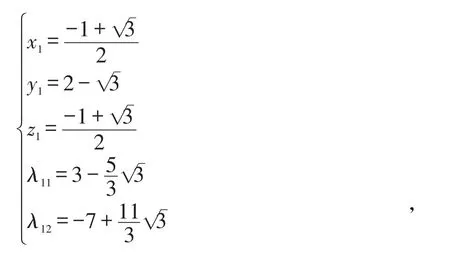
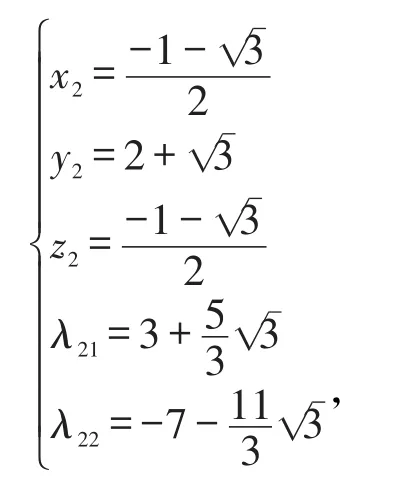
4 結論

第一，對于無條件極值的充分條件，應采用Hesse矩陣Hn作為判別矩陣；對于條件極值的充分條件，應采用Hesse變形矩陣作為判別矩陣，可判別出一部分本身是極值點但被Hn錯誤判定的駐點。產生該差別的原因是條件極值問題的自變量增量dxi均需滿足m個等式約束，所以n個dxi中只有n-m個是獨立變量，另外m個非獨立變量為這n-m個獨立變量的隱函數；而無條件極值中n個自變量增量均是獨立變量。

第二，對于條件極值問題，雖然采用判別駐點比Hn更精確，但本文給出的解析表達式仍不能判別出任一條件極值問題的所有駐點的信息。原因在于式（5）是對等式約束在駐點處作一階泰勒展開得到的關系式，舍棄了二階及其以上的高階無窮小，所求解出的非獨立變量關于獨立變量的表達式并不是最精確的。隨著目標函數維數增加，等式約束數目增多、復雜程度增大，求解式（5）已經很困難；如果再對等式約束作高階泰勒展開，解析表達式將更難或者無法解出。若想找到自變量增量間更精確的關系式，需對式（5）作高階泰勒展開直至高階無窮小量為零或近似為零，然后使用數值計算軟件求解出它們間的數值關系式，從而找到更精確的Hesse變形矩陣，方能更精確地判別出駐點的信息。雖然得不到自變量增量間最準確的解析表達式，但該判別法仍具有理論價值：指明了條件極值與無條件極值的充分條件的判別矩陣的關聯及差別，在此基礎上，給出了高維多約束狀態下一種尋找更精確的條件極值的充分條件的判別矩陣的方法。