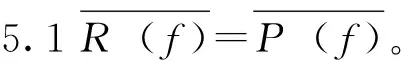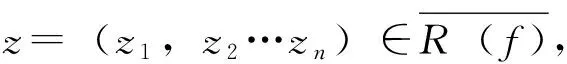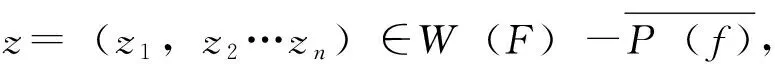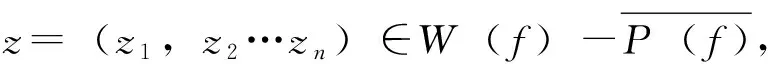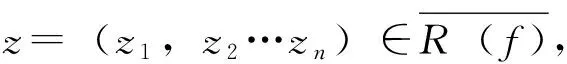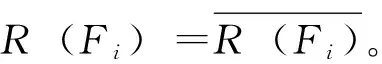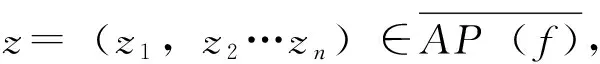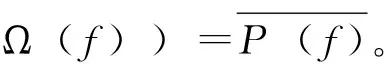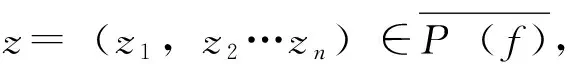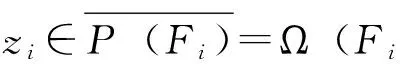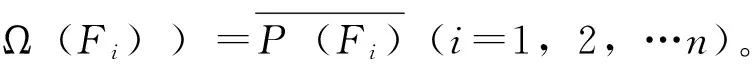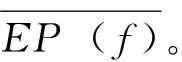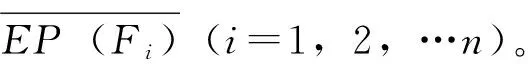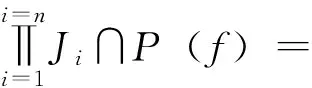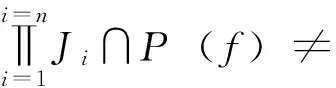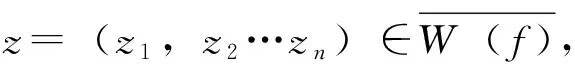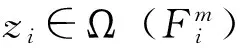N維單體上可降映射的動(dòng)力學(xué)性質(zhì)
冀占江
(梧州學(xué)院 信息與電子工程學(xué)院,廣西 梧州 543002)
1引言
在拓?fù)鋵W(xué)動(dòng)力系統(tǒng)中,一維動(dòng)力系統(tǒng)一直都是研究的重點(diǎn)和熱點(diǎn),許多學(xué)者對(duì)此進(jìn)行了研究,得到很多有意義的成果。烏克蘭數(shù)學(xué)家Sarkovskii給出了區(qū)間上著名的Sarkovskii定理,有關(guān)該定理的內(nèi)容見文獻(xiàn)[1]。1988年熊金城[2]對(duì)區(qū)間上的各種點(diǎn)集進(jìn)行了研究。Block L[3]對(duì)一維區(qū)間動(dòng)力系統(tǒng)做出了更加全面的介紹。孫太祥、席鴻建、張更容等[4]對(duì)樹映射動(dòng)力系做了詳細(xì)深入的研究。但是在實(shí)際應(yīng)用中,很多學(xué)科中出現(xiàn)的數(shù)學(xué)模型大多屬于高維乘積空間自映射的迭代問題,因此我們有必要對(duì)高維空間的動(dòng)力學(xué)性質(zhì)進(jìn)行研究。本文結(jié)合的區(qū)間映射的一些結(jié)論和可降映射的動(dòng)力學(xué)性質(zhì),給出了N維單體上可降映射的9個(gè)結(jié)論。這些結(jié)論將熊金城、周作領(lǐng)等人的研究成果更進(jìn)一步推廣,在實(shí)際中有一定的應(yīng)用價(jià)值。
2基本概念
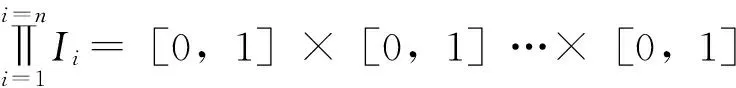
定義1[3]設(shè)(X,d)是度量空間,f∶X→X連續(xù),點(diǎn)x∈X。若存在m>0使fm(x)=x,則稱x為f的周期點(diǎn),f的周期點(diǎn)集用P(f)表示。
定義2[3]設(shè)(X,d)是度量空間,f∶X→X連續(xù),點(diǎn)x∈X。若存在m≥0使得fm(x)∈P(f),則稱x為f的終于周期點(diǎn)。f的終于周期點(diǎn)集用EP(f)表示。
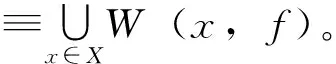
定義4[3]設(shè)(X,d)是度量空間,f∶X→X連續(xù),點(diǎn)x∈X。若x∈ω(x,f),則稱x為f的回歸點(diǎn)。f的回歸點(diǎn)集用R(f)表示。
定義5[5]設(shè)(X,d)是度量空間,f∶X→X連續(xù),點(diǎn)x∈X。若對(duì)任意的ε>0,存在y∈X和m>0,使得d(y,x)<ε且d(fm(y),x)<ε,則稱x為f的非游蕩點(diǎn)。f的非游蕩點(diǎn)集用Ω(f)表示。
定義6[3]設(shè)(X,d)是度量空間,f∶X→X是連續(xù)映射,點(diǎn)x∈X。若令ord(x,f)={fm(x)∶m≥0},則稱ord(x,f)為點(diǎn)x在f作用下的軌道。
定義7[3]設(shè)(X,d)是度量空間,f∶X→X連續(xù),x∈X。若對(duì)任意包含x的開集U,存在m>0,?k>0,?0 定義8[6]設(shè)(X,d)是度量空間,f∶X→X連續(xù),x,z∈X。稱點(diǎn)x是z的不穩(wěn)定流形點(diǎn),如果對(duì)任意包含z的鄰域V(z),存在m>0,使得x∈fm(V(z))。z的不穩(wěn)定流形點(diǎn)組成的集合叫做z關(guān)于f的不穩(wěn)定流形,記作Wu(z,f)。 定義9[7]設(shè)pi∶Xn→Ii其中pi(x)=xi,x=(x1,x2…xn),則稱pi是自然映射。 定義10[8]設(shè)f1,f2∶I→I連續(xù)映射,f∶I×I→I×I連續(xù)映射,若對(duì)任意(x1,x2)∈I×I,有F(x1,x2)=(f1(x1),f(x2)),則稱F是f1與f2的乘積映射,并記F=f1×f2。 定義11[7]設(shè)f∈C0(Xn),稱f是可降映射,如果若存在連續(xù)自映射Fi∶I→I(i=1,…n)使得pi·f=Fi·pi(i=1,2…n)成立,此時(shí)Fi(i=1,2…n)稱是f的下降組。 引理3.1設(shè)f∈C0(Xn),z=(z1,z2…zn)∈Xn,t=(t1,t2…tn)∈Xn,d是Xn上的度量,F(xiàn)i∶I→I(i=1,…n)連續(xù),則 (1)Fi是f的下降組 ?f=F1×F2×…Fn; (2)若f是可降映射,則f的下降組是唯一的; 證明:(1)的證明見參考文獻(xiàn)[8],(2),(3),(4)的證明由(1)很容易推出,(5)由(4)很容易得到。 引理3.2 設(shè)Fi(i=1,…n)是f的下降組,f∈C0(Xn),z=(z1,z2…zn)∈Xn,則 (1)設(shè)x=(x1,x2…xn)∈Xn,z∈w(x,f) ?zi∈w(xi,Fi)(i=1,2,…n)。 (2)z∈∧(f)?zi∈∧(F)(i=1,2,…n),其中∧(·)代表P(·),R(·),Ω(·),EP(·),W(·)。 證明:(1)的證明類似參考文獻(xiàn)[9]的方法;(2)Ω(·)的證明見參考文獻(xiàn)[10],P(·)的證明見參考文獻(xiàn)[11],R(·)證明方法與參考文獻(xiàn)[11]類似,EP(·)可由P(·)很容易推出;W(·)可由引理3.2(1)很容易得出。 yi∈V(Zi)∩R(Fi)(i=1,2,…n) 其他的證明方法與上面類似,在這里省略。 引理3.4設(shè)Fi(i=1,2,…n)是f的下降組,f∈C0(Xn),則∧(f)是閉集?∧(Fi)是閉集(i=1,2,…n)。∧(·)代表P(·),R(·),AP(·)。 故z∈P(f),因此P(f)是閉集,故∧(f)是閉集?∧(Fi)是閉集。 其他的證明方法與上面類似,在這里省略。 [2]、[5]、[12]給出了區(qū)間上連續(xù)自映射f的9個(gè)結(jié)論,結(jié)論如下: 引理4.7 設(shè)J?I是開區(qū)間,并且J∩P(f)=?,則J∩R(f)=?。 引理4.8W(f)是閉集。 引理4.9 若x∈Ω(f)∩EP(f),則對(duì)任意的奇數(shù)m>1,都有x∈Ω(fm)。 現(xiàn)在將區(qū)間這些結(jié)論推廣到N維單體上,設(shè)f∈C0(Xn),F(xiàn)i(i=1,2,…n)是f的下降組,則有以下結(jié)論。 由引理4.2知,Orb(zi,Fi)是無限集。由引理3.1(4)知,?m≥1,有 因此Orb(z,f)是無限集。 定理5.4AP(f)是閉集?R(f)是閉集。 引理3.2(2)知,z∈Ω(f∣Ω(f))。 另一方面:z=(z1,z2…zn)∈Ω(f∣Ω(f)),由引理3.2(2)和引理4.5知, 證明:設(shè)z=(z1,z2…zn)∈Ω(f),由引理3.2(2)和引理4.6知 定理5.8W(f)是閉集。 由引理3.2(2)可得,z∈W(f), 故W(f)是閉集。 定理5.9 若z∈Ω(f)∩EP(f),則對(duì)任意奇數(shù)m>1,都有z∈Ω(fm)。 證明:設(shè)z=(z1,z2…zn)∈Ω(f)∩EP(f),則有zi∈Ω(Fi)∩EP(Fi)(i=1,2,…n)。 [參考文獻(xiàn)] [1] 張仲景, 熊金成.函數(shù)迭代與一維動(dòng)力系統(tǒng)[M].成都: 四川教育出版社, 1992. [2] 熊金成.線段映射的動(dòng)力體系: 非游蕩集, 拓?fù)潇匾约盎靵y[J].數(shù)學(xué)進(jìn)展, 1988, 17(1): 1-11. [3] Block L S, Coppel W A.Dynamics in one dimension[M].Berlin: Springer-Verlag, 1992. [4] 孫太祥, 席鴻建, 張更容,等.樹映射的動(dòng)力學(xué)[M].南寧: 廣西科學(xué)技術(shù)出版社, 2011. [5] 廖公夫, 王立冬, 范欽杰.映射迭代與混沌動(dòng)力系統(tǒng)[M].北京: 科學(xué)出版社, 2013. [6] 金渝光.一類二維自映射無異狀點(diǎn)的又一充要條件[J].重慶師范大學(xué)學(xué)報(bào)(自然科學(xué)版),1994,11(1):12-15. [7] 杜瑞瑾, 金渝光, 李梅霞.關(guān)于一類維自映射的周期點(diǎn)集[J].重慶工商大學(xué)學(xué)學(xué)報(bào)(自然科學(xué)版), 2006,23(1): 12-14. [8] 黎日松.可降映射的一些動(dòng)力學(xué)性質(zhì)[J].太原理工大學(xué)學(xué)報(bào): 2006, 37(4): 498-500. [9] 杜瑞瑾.一類n維自映射有異狀點(diǎn)的充要條件[J].哈爾濱商業(yè)大學(xué)學(xué)報(bào)(自然科學(xué)版), 2006,22(4):124-125. [10] 斯琴巴特爾.也談單位正方形到自身的一類映射的中心深度[J].內(nèi)蒙古民族師院學(xué)報(bào)(自然科學(xué)版),1996, 11(2): 131-132. [11] 晏炳剛.可降映射的混沌集與漸進(jìn)周期點(diǎn)[J].河北工程大學(xué)學(xué)報(bào)(自然科學(xué)版), 2007, 24(3): 101-103. [12] 周作領(lǐng).一維動(dòng)力系統(tǒng)[J].數(shù)學(xué)季刊, 1988, 3(1): 42-65. [13] 熊金成.線段映射的動(dòng)力體系:非游蕩集, 拓?fù)潇匾约盎靵y[J].數(shù)學(xué)進(jìn)展, 1988,17(1):1-11.3若干個(gè)引理
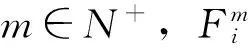
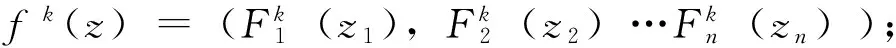

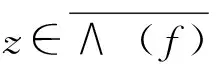
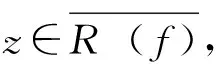
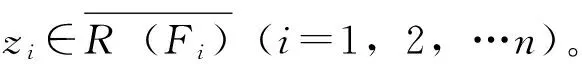

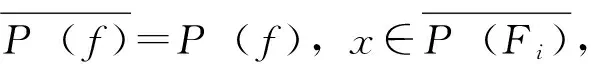
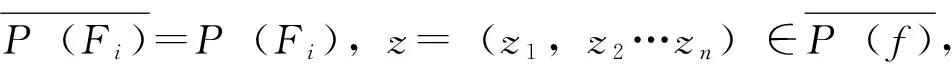
4區(qū)間I=[0,1]上一些結(jié)論
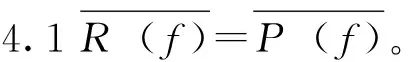
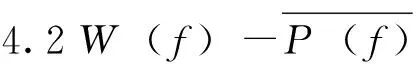
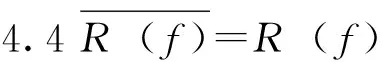
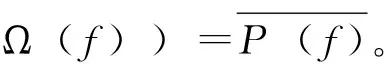
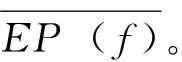
5主要定理