單層球面網殼火災爆炸動力響應

賀擁軍+周冬星+周緒紅

摘 要：以K8型單層球面網殼為研究對象，考慮幾何非線性和溫度對材料性能的影響，完整模擬了單層球面網殼在發(fā)生火災的不同階段受到爆炸沖擊作用時的動力性狀。據B-R準則，通過爆炸峰值超壓與結構動力特征響應之間的關系，可判定K8型單層球面網殼在不同火災階段，爆炸沖擊作用下的動力穩(wěn)定性臨界峰值超壓。分析了單層球面網殼的矢跨比、屋面荷載、約束布置等參數(shù)對其在不同火災階段的爆炸沖擊動力穩(wěn)定性的影響。研究表明：火災對網殼結構在爆炸沖擊作用下的動力穩(wěn)定性有較大影響，當網殼桿件最高溫度達500 ℃以上時，結構的抗爆能力明顯降低。矢跨比、屋面質量、約束布置對網殼在火災不同階段的抗爆能力均有不同程度的影響。

關鍵詞：球面網殼；火災；爆炸沖擊；動力響應

中圖分類號：TU392.3 文獻標志碼：A 文章編號：1674-4764（2018）01-0055-07

Dynamic response of single-layer reticulated domes under fire and blast loads

He Yongjun1，Zhou Dongxing1，Zhou Xuhong2

（1.College of Civil Engineering， Hunan University， Changsha 410082，P.R.China；2. School of Civil Engineering，Chongqing University， Chongqing 400045，P.R.China）

Abstract：The Kiewitt-8 single-layer reticulated domes were taken as case study. Considering the influence of geometric nonlinearity and temperature on the properties of the material， the dynamic behavior of the single-layer reticulated domes subjected to blast loading in different fire stages was simulated. According to the B-R criterion， the dynamic stability critical overpressure loads of K8 single-layer reticulated domes subjected to blast loading in different fire stages could be determined by the relationship between the peak overpressure of blast and the structural dynamic response. And the influence of parameters such as the rise-span ratio， the roof load and the constraint settings on the dynamic stability of single-layer reticulated domes subjected to blast loading in different fire stages were analyzed. The results show that fires have a great influence on the dynamic stability of the reticulated domes under the impact of explosion， When the maximum temperature of the reticulated dome rods rises to more than 500℃， the anti-explosion ability of the dome greatly decreases. The rise-span ratio， the roof load and the restraint settings have different effects on the anti-blast ability of the reticulated domes in different fire stages.

Keywords：reticulated domes； fire； blast loading； dynamic response

網殼結構具有自重輕、結構剛度好等特點，往往被廣泛運用于覆蓋面積較大的空間，如大型體育館、展覽館等。近些年，恐怖分子針對人口活動密集的大型場館的破壞襲擊時有發(fā)生，一旦遭遇襲擊，引起火災甚至火災下的爆炸，將造成嚴重的后果。關于火災下大空間溫度場分布，利用有限元軟件可以較好地模擬大空間建筑在發(fā)生火災時的溫度分布[1-3]，李國強等[1]根據模擬數(shù)據，總結歸納得出了實用的大空間火災升溫經驗公式。學者們利用有限元軟件對鋼結構或大跨鋼結構在火災下的性能進行了研究，研究表明火災對鋼結構材料性能有較大影響[4]，同時，火源位置、功率以及燃燒速率等都對網殼結構火災下的整體性能較大影響[5-7]，針對鋼構件的高溫分析與網殼結構整體分析發(fā)現(xiàn)，鋼結構的耐火時間不超過2 h[8-9]。在網殼結構抗爆研究方面，文獻[10-11]采用簡化爆炸荷載模型的方式，對網殼結構在爆炸作用下的結構性能進行有限元模擬，并討論了有限元方法分析網殼抗爆性能的可行性；文獻[12-13]對矢跨比、爆炸點、炸藥量對網殼結構抗爆性能的影響進行了研究。endprint

網殼結構在火災下的性能與網殼結構在爆炸沖擊下的性能的研究往往分開討論，而實際情況中火災與爆炸沖擊往往是耦合地對結構造成破壞，更加復雜。因此，對單層球面網殼結構在火災爆炸沖擊耦合作用下的結構動力響應，以及結構在不同火災階段的臨界爆炸峰值超壓的研究極具現(xiàn)實意義。

采用ANSYS/LS-DYNA，以高大空間建筑火災作用下空氣升溫實用公式為基礎，模擬分析了單層球面網殼在發(fā)生火災的情況下耦合爆炸沖擊超壓作用的動力響應，并根據結構動力穩(wěn)定判定準則[14-16]，確定了在火災的不同階段，單層球面網殼的動力穩(wěn)定臨界爆炸峰值超壓；討論了矢跨比、屋面質量、約束條件等參數(shù)對單層球面網殼火災爆炸下動力穩(wěn)定性的影響。

1 網殼動力穩(wěn)定判定方法及模擬正確

性驗證

1.1 動力穩(wěn)定判定方法

B-R準則[14]可以描述為：通過大量的逐級加載，由系統(tǒng)運動方程獲得位移與荷載的關系，將微小位移變化引起結構位移突然增加時的荷載定義為臨界荷載，其本質是Liapunov意義上的運動失穩(wěn)；只要位移荷載曲線的拐點足夠明顯，Budiansky建議把曲線的拐點作為動力屈曲的臨界點。采用B-R準則對網殼在火災爆炸情況下的動力穩(wěn)定性進行判定，具體實現(xiàn)方法如下：在對網殼結構進行全過程火災模擬的過程中，選擇網殼桿件最高溫度分別達到20、100、200、300、400、500 ℃的時間點，對網殼結構施加爆炸沖擊超壓荷載，以研究網殼在發(fā)生火災不同階段的抗爆能力。通過所施加的爆炸峰值超壓荷載與網殼節(jié)點最大位移之間的關系曲線，采用B-R準則對網殼的動力穩(wěn)定進行判定，得到火災不同階段下，網殼結構的臨界爆炸峰值超壓。

1.2 有限元模擬正確性驗證

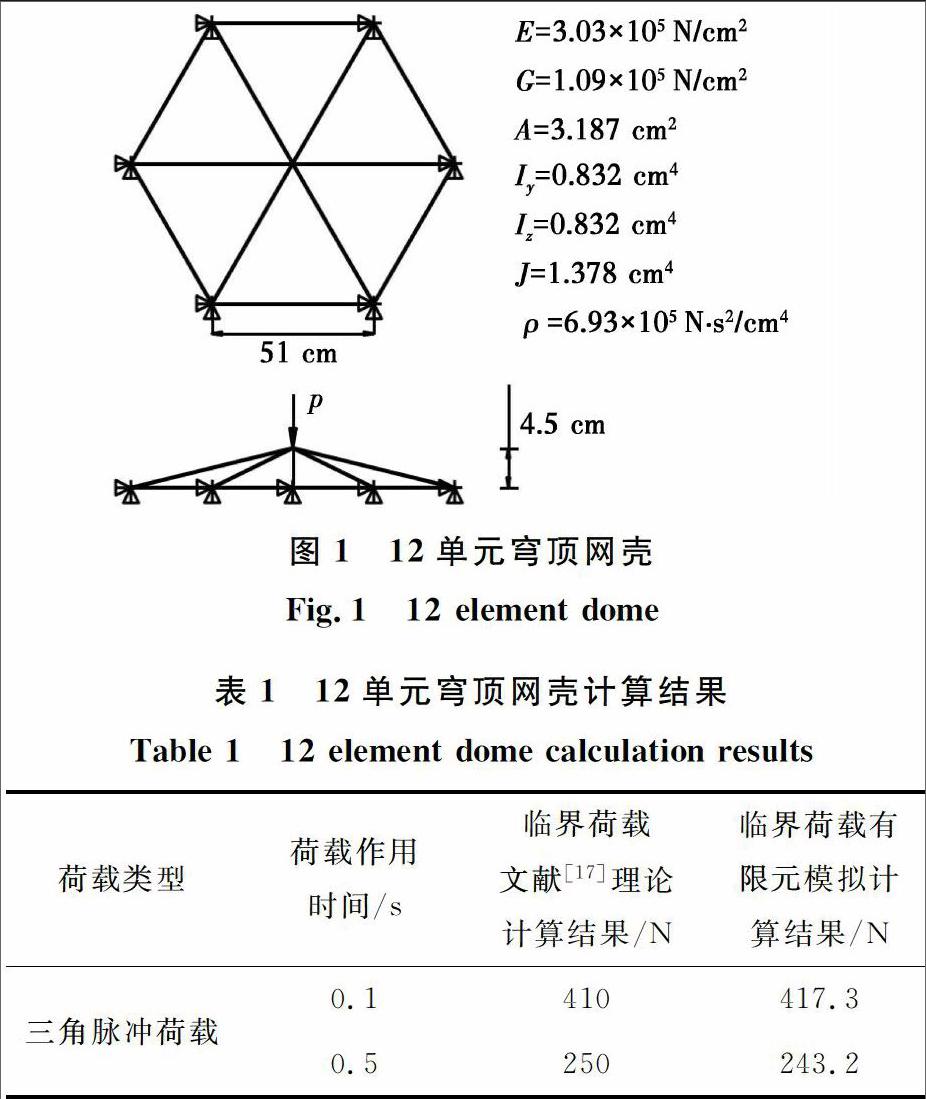
通過典型算例，考察所采用的有限元模擬方法的正確性。運用有限元軟件，采用瞬態(tài)動力分析中的完全法，針對圖1所示的網殼施加三角脈沖荷載，根據B-R準則得到其動力穩(wěn)定臨界荷載，并與文獻[17]采用理論計算所得臨界荷載進行比較，如表1。對比可知，所采用的有限元模擬分析方法計算結果與典型算例結果較為吻合。

2 火災爆炸作用下單層K8球面網殼動力穩(wěn)定性

2.1 有限元模型

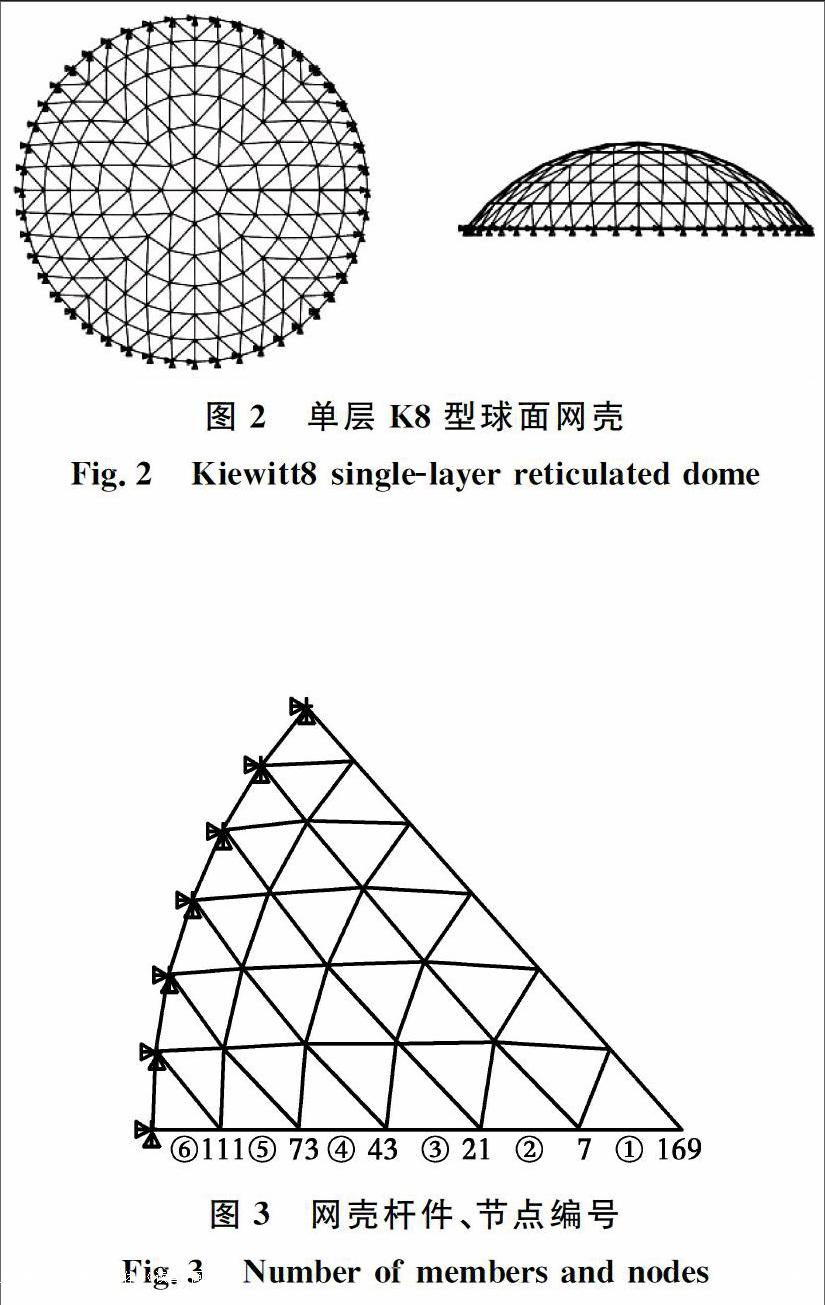
采用的分析對象為單層K8型球面網殼，如圖2所示；跨度為40 m，矢跨比為1/4，考慮火源位置及爆炸點處于網殼中心正下方，距離網殼頂點15 m處。網殼的徑向分頻數(shù)為6；主徑向和環(huán)向桿件截面均為Φ121 mm×4.0 mm。

網殼采用周邊支座采用固端約束，桿件單元及節(jié)點編號如圖3所示。

2.2 火災空氣升溫和鋼構件升溫模型

采用歐洲規(guī)范[18]，對鋼材在高溫下的熱膨脹系數(shù)、導熱系數(shù)、比熱等物理特性和屈服強度、彈性模量的折減系數(shù)、應力應變關系等力學性能進行計算取值，圖4為不同溫度下鋼材應力應變曲線，火災全過程模擬中，通過將火災下桿件溫度時間變化曲線轉化為隨時間變化的溫度荷載施加于相應桿件，從而模擬高溫下鋼材的材料性能隨溫度的變化效應。

依據李國強、杜詠針對高大空間建筑火災升溫經驗公式的研究，即中國《建筑鋼結構防火技術規(guī)程》對網殼結構火災下內部空氣升溫采用高大空間建筑火災作用下空氣升溫實用公式，基于高大空間火災數(shù)據統(tǒng)計及《建筑鋼結構防火技術規(guī)程》，本文考慮火源功率類型為大功率，火災增長類型為快速。考慮無保護層取初始溫度為20 ℃。

得到火災發(fā)生至6 000 s內單層球面網殼各桿件的升溫曲線，以主徑向6根桿件為例，火災下桿件溫度時間曲線如圖5所示。

2.3 火災過程中爆炸超壓作用下動力分析

通過ANSYS有限元模擬，采用瞬態(tài)動力分析中的完全法對網殼結構進行火災下爆炸沖擊動力分析，考慮網殼屋面荷載為1.0 kN/m2，轉換為質量單元施加于節(jié)點上，考慮大變形和大轉角；采用Rayleigh阻尼，阻尼比為0.02。

以全時程動力方式將火災下鋼構件的升溫曲線作為隨火災時間變化的溫度荷載施加于網殼桿件。結合抗爆動力學相關理論[19]，簡化爆炸時產生的超壓時程曲線為三角脈沖超壓荷載時程曲線，如圖6，假定其均布作用于網殼球面，方向從球心垂直球面向外；設定爆炸沖擊作用時間為0.1 s，采用自動時間步長進行模擬計算。

根據網殼桿件最高溫度值將火災全過程分為6個階段，即網殼桿件最高溫度分別達到20、100、200、300、400、500 ℃等6個階段。在上述的6個階段分別對網殼結構進行大量的逐級加載的爆炸沖擊模擬，根據B-R準則，探究網殼結構在火災不同階段的臨界爆炸峰值超壓。

選取圖3所示的主徑向6個節(jié)點為位移測點，按上述的6個階段分別進行爆炸沖擊模擬，記錄不同爆炸峰值超壓下位移測點的最大位移響應，將所得的數(shù)據分別繪制成不同火災溫度階段下網殼結構節(jié)點位移爆炸峰值超壓曲線，如圖7所示。可以看出，不同火災溫度階段下網殼結構節(jié)點位移爆炸峰值超壓曲線均體現(xiàn)為3個階段，即爆炸沖擊對網殼結構穩(wěn)定的影響階段。以火災溫度為300 ℃階段下爆炸沖擊模擬所得節(jié)點位移時程曲線為例，如圖8所示，網殼結構在不同的爆炸超壓作用下的位移響應可以分為3個階段：

1）彈性階段 該階段的爆炸峰值超壓值較小，網殼在經受爆炸峰值超壓之后，位移能夠得到恢復；該階段的位移量較小，以高溫下的熱膨脹為主。

2）塑性階段 該階段網殼經受爆炸后，產生塑性積累，網殼中心附近節(jié)點的位移不能恢復，網殼整體剛度降低。

3）破壞階段 爆炸峰值荷載已達到網殼的臨界爆炸峰值超壓，節(jié)點位移突然陡增，結構已被破壞。

此外，由圖7所得數(shù)據，根據B-R準則，可以得到火災不同階段，單層球面網殼的臨界爆炸峰值超壓，如圖9所示。可以看出，在桿件最高溫度達在20～400 ℃的溫度區(qū)間時，網殼的臨界爆炸峰值超壓隨溫度略有下降；當桿件最高溫度達到500 ℃時，臨界爆炸峰值超壓下降非常明顯，此時網殼所有桿件溫度均達300 ℃以上，整體剛度下降幅度較大，導致臨界爆炸峰值超壓發(fā)生陡降。endprint

3 不同參數(shù)對單層球面網殼火災爆炸

性能的影響

3.1 矢跨比

選定跨度為60 m的單層球面網殼，通過改變矢高，對矢跨比分別為1/4、1/5、1/6、1/7的單層球面網殼進行對比分析。

根據高大空間建筑火災作用下空氣升溫實用公式，針對不同矢跨比的網殼空間進行計算，得到不同矢跨比網殼桿件溫度時間關系。

經過大量的爆炸沖擊模擬，依據B-R準則得到矢跨比分別為1/4、1/5、1/6、1/7的單層球面網殼在火災不同溫度階段下的臨界爆炸峰值超壓，見表2。

隨矢跨比的減小，單層球面網殼在火災不同階段的臨界爆炸峰值超壓荷載呈下降趨勢。這是由于隨著矢跨比減小，網殼結構在爆炸沖擊方向的整體剛度下降所導致。同樣的不同矢跨比網殼隨著溫度升高，其抗爆性能均呈下降趨勢。

3.2 屋面質量

以跨度為40 m、矢跨比為1/4的單層球面網殼為例，研究不同屋面質量對單層球面網殼火災爆炸作用下的臨界爆炸峰值超壓的影響。上文已研究屋面荷載為1.0 kN/m2的情況，本節(jié)增加考慮無屋面質量荷載和屋面質量荷載為2.0 kN/m2和3.0 kN/m2的情況。

經過大量模擬爆炸沖擊得到跨度為40 m、矢跨比為1/4的單層球面網殼在不同屋面質量荷載下，火災爆炸情況中的臨界爆炸峰值超壓，如表3。

屋面質量對網殼的抗爆性能存在一定的影響。由于爆炸超壓作用方向與屋面質量荷載的作用方向相反，所以，網殼結構的抗爆性能隨屋面質量的增加而提升。隨著網殼桿件溫度的上升，網殼結構臨界爆炸峰值超壓的下降逐漸明顯。

3.3 約束條件

支座約束條件也是影響火災爆炸作用下網殼結構動力性能的重要參數(shù)之一。網殼均采用將所有邊緣節(jié)點固定鉸支約束的方式，以跨度40 m、矢跨比為1/4的單層球面網殼為例，采用固定鉸支座，分別對網殼邊緣的8、16、24個節(jié)點進行固定鉸支約束，如圖10所示，進行火災爆炸作用下的動力分析。

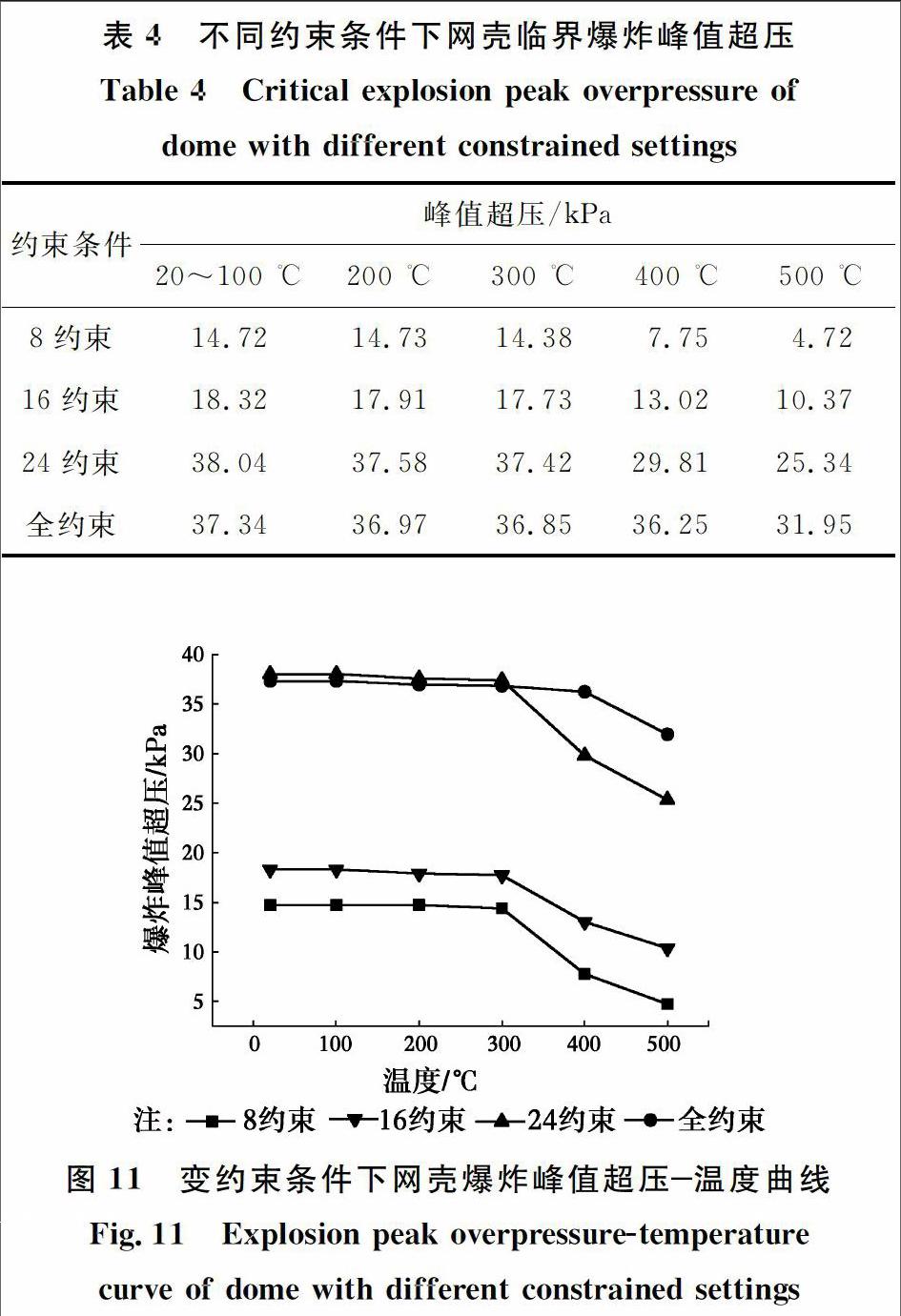
得到不同約束條件下單層球面網殼在火災不同階段的爆炸峰值超壓，見表4和圖11。根據表4和圖11數(shù)據可知：

1）在采用8約束與16約束情況下，由于網殼約束支座設置較少，導致結構的整體剛度偏小，網殼的臨界爆炸峰值超壓在各個火災階段均偏低，且當桿件最高溫度達到400 ℃后，結構剛度發(fā)生明顯下降，其抗爆性能也隨之顯著降低。

2）當約束支座設置增加至24個節(jié)點時，網殼結構的自由度降低，結構剛度增加，網殼在各個火災階段的抗爆性能明顯提高。結構整體剛度和抗爆性能也在桿件最高溫度達到400 ℃后顯著降低。

3）24約束情況下與全約束情況進行對比發(fā)現(xiàn)，當網殼桿件最高溫度在20～300 ℃區(qū)間內，24約束的網殼抗爆性能略優(yōu)于全約束的網殼；但桿件最高溫度達到400 ℃以后，24約束的網殼整體剛度的下降幅度超過全約束網殼，導致其抗爆性能下降更為明顯。

4 結論

對單層球面網殼在火災爆炸作用下的動力穩(wěn)定性進行了研究。得到以下結論：

1）以高大空間實用火災升溫公式為基礎，采用火災全過程模擬耦合爆炸沖擊的方式，可以進行網殼在火災高溫與爆炸沖擊共同作用下的全過程模擬分析。

2）通過爆炸峰值超壓與網殼結構位移之間的關系曲線，可以掌握網殼結構隨爆炸峰值超壓的增大、結構動力性狀不斷變化直至失穩(wěn)的全過程。根據B-R準則可以判定單層球面網殼在火災不同溫度階段的爆炸沖擊臨界超壓荷載。

3）矢跨比對網殼在火災爆炸作用下的動力性能有較大的影響，隨著矢跨比的減小，網殼在火災爆炸作用下的動力穩(wěn)定性能降低，屋面質量對網殼在火災爆炸作用下的動力穩(wěn)定性能有一定的影響。約束條件對網殼在火災爆炸作用下的動力穩(wěn)定性影響較大。約束設置越多的網殼在較高溫度階段的抗爆能力越強。

參考文獻：

[1] 李國強，杜詠. 實用大空間建筑火災升溫經驗公式[J].消防科學與技術，2005，24（3）：283-287.

LI G Q， DU Y. Experimental formula for fire temperature rise in large space building [J]. Fire Science and Technology， 2005，24 （3）： 283-287.（in Chinese）

[2] YIN B， YANG H， SHI Y， et al. Temperature field distribution of large-space structures under various fire scenarios[J]. Journal of Tsinghua University， 2011， 51（8）：1122-1127.

[3] 于志超，朱國慶，田承飛. 大空間溫度場預測模型與實驗分析[J]. 消防科學與技術，2016，35（10）：1372-1375.

YU Z C， ZHU G Q， TIAN C F. Prediction model and experimental analysis of large space temperature field [J]. Fire Science and Technology， 2016，35（10）： 1372-1375.（in Chinese）

[4] IU C K. Nonlinear fire analysis of steel structure using equivalent thermal load procedure for thermal geometrical change [J]. Fire Safety Journal， 2016， 86：106-119.endprint

[5] YANG L， FENG X U. Numerical calculation of temperature rise in the large space grid structure under local fire conditions[J]. Fire Science & Technology， 2014，43：21-30.

[6] BAI Y，ZHAI J L，SHI Y J，et al. Analysis of overall stability bearing capacity of single-layer shell structures under high temperature condition[J].Science China Technological Sciences，2013，56：751-757.

[7] 劉東宇， 劉紅波， 廖祥偉. 茌平體育館弦支穹頂疊合拱復合結構抗火性能分析[J]. 工業(yè)建筑， 2016， 46（11）：7-12.

LIU D Y， LIU H B， LIAO X W. Fire resistance of chord dome composite arch structure in chiping gymnasium [J]. Industrial Buildings， 2016， 46 （11）： 7-12.（in Chinese）

[8] WITA P， KAMIńSKI M. Probabilistic buckling analysis of the beam steel structures subjected to fire by the stochastic finite element method[J]. International Journal of Applied Mechanics and Engineering，2016，21（1）：485-510.

[9] 薛素鐸， 王廣勇. 凱維特單層球面網殼抗火性能研究[J]. 工業(yè)建筑， 2008（Sup1）：452-454.

XUE S D， WANG G Y.Study on fire resistance of KeweiTe single-layer spherical reticulated shell [J]. Industrial Architecture， 2008 （Sup1）： 452-454. （in Chinese）

[10] MA J L，WU C Q， ZHI X D，et al. Prediction of confined blast loading in single-layer lattice shells[J]. Advances in Structural Engineering，2014，17（7）：1029-1044.

[11] 韓慶華，金曉東. 爆炸荷載作用下單層球面網殼結構的動力穩(wěn)定性[C]// 天津大學、上海交通大學. 第十屆全國現(xiàn)代結構工程學術研討會論文集，2010：9.

HAN Q H， JIN X D. Dynamic stability of single-layer reticulated shells under explosive loading[C]// Tianjin University， Shanghai Jiaotong University.Tenth National Modern Structural Engineering Symposium Proceedings， 2010： 9. （in Chinese）

[12] 高軒能，李超，江媛. 單層球面鋼網殼結構在內爆炸作用下的動力響應[J]. 天津大學學報（自然科學與工程技術版），2015（Sup1）：102-109.

GAO X N， LI C， JIANG Y. Dynamic response of single-layer reticulated dome structure under internal explosion [J]. Journal of Tianjin University （Natural Science and Engineering Technology）， 2015（Sup1）： 102-109. （in Chinese）

[13] 馬加路，支旭東，范峰，等.外爆荷載下Kiewitt-8型單層球面網殼的動力響應[J]. 振動與沖擊，2015，34（21）：65-70.

MA J L， ZHU X D， FAN F， et al. Dynamic response of Kiewitt-8 single-layer reticulated dome under external explosive loading[J]. Vibration and Shock， 2015，34（21）： 65-70. （in Chinese）

[14] BA P F，ZHANG Y G，WU J Z， et al. The failure criterion of single-layer spherical lattice shell based on kinetic energy[J]. Mathematical Problems in Engineering，2015（1）：1-7.

[15] HUI J L， YANG L F，LUO Y F. Dynamic stability of large-span suspen-domessubjected to seismic excitations[J]. Advanced Materials Research，2012，378-379：209-212.

[16] 王策， 沈世釗. 單層球面網殼結構動力穩(wěn)定分析[J]. 土木工程學報， 2000， 33（6）：17-24.

WANG C， SHEN S Z.Dynamic stability analysis of single-layer spherical reticulated shells [J].Chinese Journal of Civil Engineering， 2000， 33 （6）： 17-24. （in Chinese）

[17] 孫建恒， 夏亨熹. 網殼結構非線性動力穩(wěn)定分析[J]. 空間結構， 1994（1）：25-31.

SUN J H， XIA H X. Nonlinear dynamic stability analysis of reticulated shell structure [J]. Space Structures， 1994 （1）： 25-31. （in Chinese）

[18] European committee for standardization，ENV 1993-1-2，Eurcode 3，Design of Steel Structures，Part1.2：Structural Fire Design[S]. 1993.

[19] 李國豪. 工程結構抗爆動力學[M]. 上海：上海科學技術出版社，1989：167.

LI G H.Anti-explosive dynamics of engineering structures[M]. Shanghai： Shanghai Science and Technology Press， 1989： 167. （in Chinese）endprint