基于輸入時延的線性連續時不變系統量化分析與控制*

陳 俊，陳海飛，高金鳳

(浙江理工大學 機械與自動控制學院，浙江 杭州 310018)

0 引 言

網絡控制系統是一種將空間分布的多個系統元件如：傳感器、執行器、控制器等控制節點通過數字通信網絡連接的閉環反饋控制系統[1]。由于控制系統回路中通信網絡的介入，不可避免地將網絡其本身帶寬有限等特性引入到控制系統中，必須設計出先進的控制策略。

針對時延和丟包控制問題，LI等[2]提出了一種改進的依賴時延上界和丟包上界的穩定性判據；XIE等[3]將通信受限的NCSs建模成具有輸入時延的離散時間切換系統，通過求解一組線性矩陣不等式(LMIs)獲得了系統的穩定性條件；ZHANG等[4]基于Markov建模方法，將傳感器到控制器和控制器到執行器的兩段傳輸時延分別建模成兩個Markov鏈，并分析了閉環系統的隨機穩定性。與此同時，Zhang等[5]考慮了一類時變時延小于一個采樣周期的NCSs，進而將系統描述成離散時間切換系統，設計了相應的H∞控制器使系統達到指數均方穩定和指定的H∞性能，并建立了時延長度，時延變化頻率和閉環系統性能的關系。

另一方面，在接收端恢復出信號與原信號有一定的誤差。早期ELIA等[6]指出在單輸入單輸出的離散線性時不變系統中，對數量化器是最粗糙的量化器，得到了系統穩定的最小量化密度跟系統自身的不穩定極點有關、QU等[7]研究了離散線性無線網絡控制系統的穩定性，基于Markov跳變系統，將系統穩定性轉化為一個等價的不確定系統的魯棒穩定性問題；JIANG等[8]同時考慮了網絡誘導時延，數據包任意丟失，量化的影響，基于已知的丟包概率，時延的上下界和量化密度，設計了統一的控制率。以上文獻都是考慮了傳感器對被控對象采樣的狀態信息傳輸到控制器端的量化情況，而在實際系統中，控制器的輸出信號在送到執行器端前也同樣需要量化。

本研究將對系統建模、穩定性分析及控制器設計3個方面進行研究。

1 系統建模

考慮被控對象為線性時不變系統，其狀態方程如下：

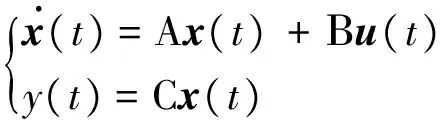
(1)

式中：x(t)—被控系統的狀態向量x(t)∈Rn；u(t)—控制輸入，u(t)∈Rp；y(t)—被控輸出，y(t)∈Rr；A,B,C—具有適當維數的常數矩陣。

具有時延和量化的網絡控制系統的結構如圖1所示。

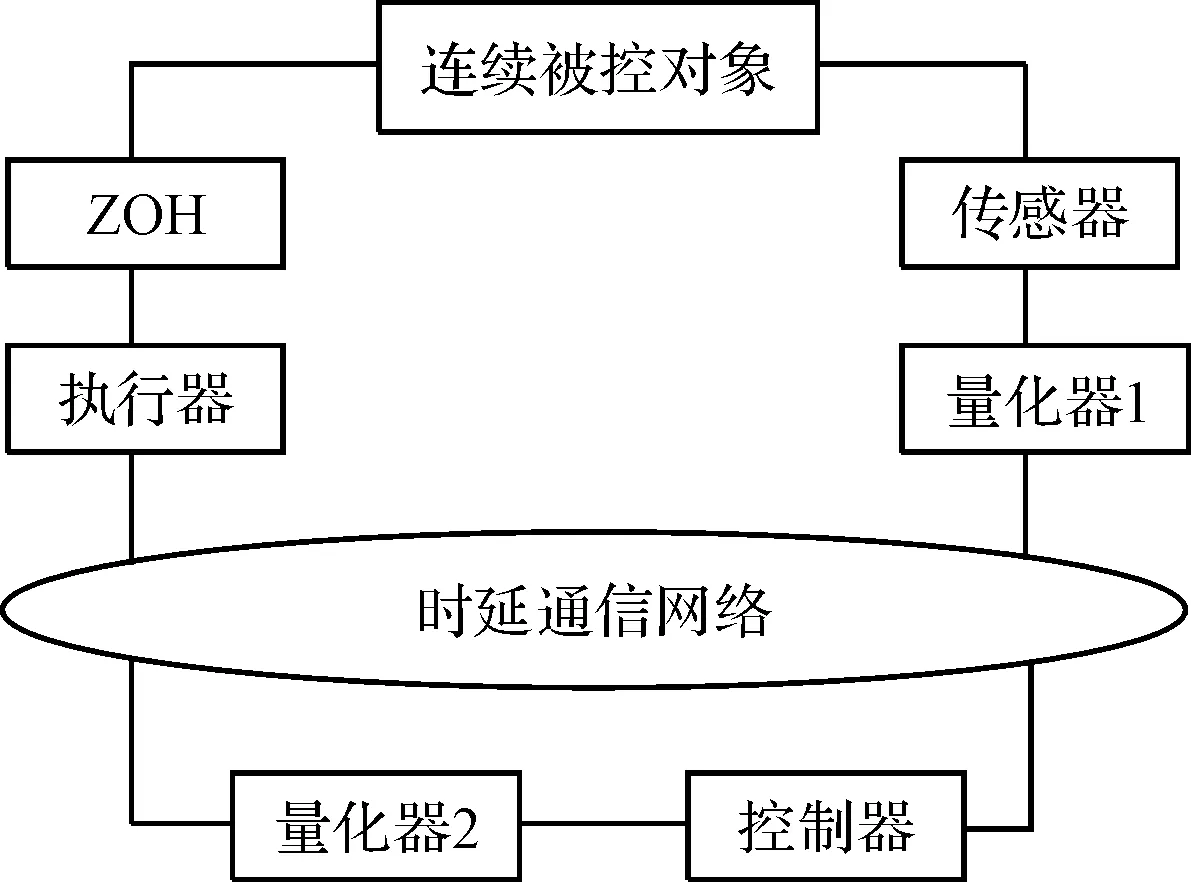
圖1 具有時延和量化的網絡控制系統的結構

為了不失一般性，對NCSs作如下假設：

假設1：網絡時延在兩個通道中都存在，用u(t+)=Κx(t-τsc(k))表示傳感器到控制器時延，用u(t+)=Κx(t-τsc(k))表示控制器到執行器時延，兩部分的總時延用u(t+)=Κx(t-τsc(k))表示，即u(t+)=Κx(t-τsc(k))。u(t+)=Κx(t-τsc(k))是有界的，即ηm≤τ(k)≤ηM,u(t+)=Κx(t-τsc(k))。

假設2：數據在每個采樣周期內以單包的形式傳輸。傳感器是時鐘驅動，而控制器和執行器都是事件驅動。

假定被控系統的狀態都是可觀測的，則可以使用閉環狀態反饋控制器:

u(t+)=Κx(t-τsc(k))，k=1,2,…

(2)

式中：Κ—狀態反饋增益。

由于通信網絡中存在網絡誘導時延和數據包丟失的問題，將式(2)代入式(1)中得到：

(3)

式中：t∈[ikh+τ(k),ik+1h+τ(k+1)]；h—采樣周期；x(ikh)—系統狀態x(t)在采樣時刻ikh經傳感器檢測出的信號。

由于零階保持器(ZOH)的工作機制[9]，u(ikh)在采樣時刻ikh總是接收最新的控制信號以保證系統的實時性，又因為x(ikh)=x(t-(t-ikh))，令η(t)=t-ikh，其中，t∈[ikh+τ(k),ik+1h+τ(k+1)]，根據假設1可知，ηm≤(ik+1h-ikh)+τ(k+1)≤ηM，所以η(t)也是有界的，即ηm≤η(t)≤ηM。結合式(1～3)，并用t-η(t)代替ikh，于是式(3)可以表示為：

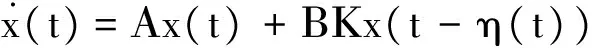
(4)

其中：t∈[ikh+τ(k),ik+1h+τ(k+1)]，ηm≤η(t)≤ηM。

考慮到前饋通道和反饋通道分別加入量化器后，量化器g(·)和f(·)分別量化狀態信號和控制信號，量化器與其兩端的輸入輸出關系描述如下：

v(t)=Κg(x(ikh))

(5)

u(t)=f(v(t))

(6)

量化器f(·)和g(·)定義為：

f(v)=[f1(v1),f2(v2),…,fp(vp)]T

(7)

g(x)=[g1(x1),g2(x2),…,gn(xn)]T

(8)

其中：fi(·)和gj(·)(i=1,2,…,p;j=1,2,…,n)是對稱的，即fi(-vi)=-fi(vi)和gj(-xj)=-gj(xj)，本文選取fi(·)和gj(·)為對數量化器。

定義1[10]：一個量化器被稱為對數量化器，它的量化級數的集合為：

U={±ui：ui=ρiu0,i=±1,±2,…}∪
{±u0}∪{0},0<ρ<1,u0>0

(9)

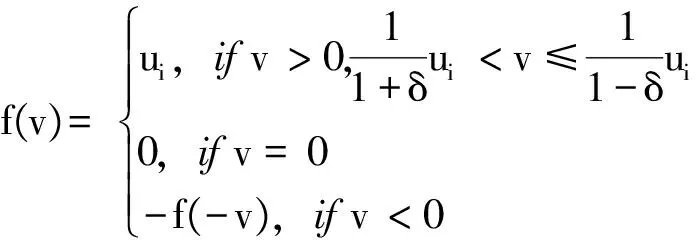
定義為：

(10)

其中：

(11)

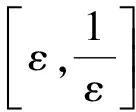
(12)

利用扇形界方法可將fi(·)和gj(·)表示為[11]：

fi(vi)=(1+Δfi(vi))vi，|Δfi(vi)|≤δfi

(13)

gj(xj)=(1+Δgj(xj))xj，|Δgj(xj)|≤δgj

(14)

于是量化器fi(·)和gj(·)可以表示為：

f(v)=(Ι+Δf)v

(15)

g(x)=(Ι+Δg)x

(16)

其中：令Δf=Δfi，Δg=Δgj，Ι為適當維數的單位陣。根據式(1～4，15-16)得到系統的控制輸入為：

u(t)=(Ι+Δf)Κ(Ι+Δg)x(ikh)=
(Κ+Δ(Κ))x(ikh)

(17)

其中，Δ(Κ)=ΔfΚ+ΚΔg+ΔfΚΔg。結合式(4)和式(17)得到：

(18)

其中：t∈[ikh+τ(k),ik+1h+τ(k+1)]。

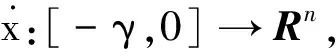
(19)

引理2[12]：對于給定的具有適當維數的矩陣Ω1，Ω2和Ψ，σ(t)是關于t的函數，且滿足0≤σm≤σ(t)≤σM，則：(σ(t)-σm)Ω1+(σM-σ(t))Ω2+Ψ<0成立當且僅當：(σM-σm)Ω1+Ψ<0，(σM-σm)Ω2+Ψ<0。

引理3[13]：對于給定的適當維數的實矩陣D，E和F且滿足‖F‖≤1，則對任意給定的變量ε>0，有下面的不等式成立：

DEF+ETFTDT≤ε-1DDT+εETE

(20)

2 穩定性分析

定理1給出了其漸近穩定的一個判據，為接下來的控制器設計提供了理論基礎。

定理1：給定狀態反饋增益矩陣Κ和標量常數ηm，ηM，如果存在適當維數的對稱正定矩陣P>0，Ti>0，Mi>0(i=1,2)和普通矩陣S，N滿足式(21～22)，則閉環控制系統(18)是漸近穩定的。

(21)

(22)

其中：

證明：選取的Lyapunov-Krasovskii泛函形式：

V(t)=V1(t)+V2(t)+V3(t)

其中：

V1(t)=xT(t)Px(t)

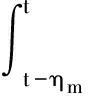
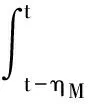
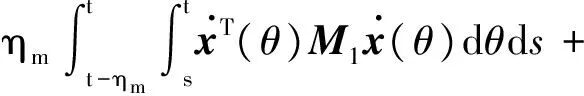
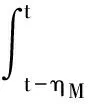
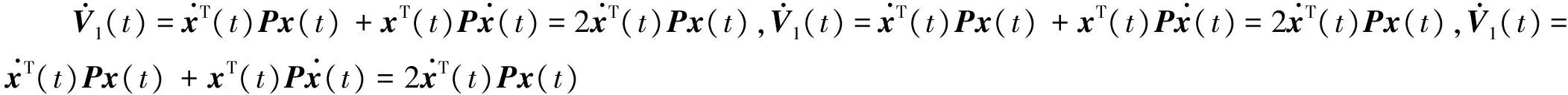
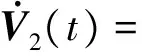
xT(t)T2x(t)-xT(t-ηM)T2x(t-ηM)

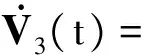
2φT(t)S[x(t-ηm)-x(t-η(t))-

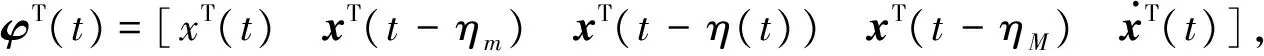
(23)

另外，其中兩項：

(24)

(25)

結合式(23～25)可得：

xT(t-ηm)T1x(t-ηm)-

(x(t)-x(t-ηm))TM1(x(t)-x(t-ηm))-

2φT(t)S(x(t-ηm)-x(t-η(t)))+

2φT(t)N(x(t-η(t))-x(t-ηM))+

(26)

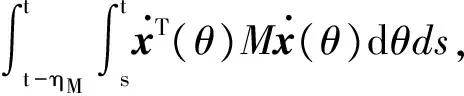
由于Δ(Κ)=ΔfΚ+ΚΔg+ΔfΚΔg是以非線性的形式存在的，其中的Δf和Δg為兩個不確定項，Δ(K)也是不確定的，無法直接用Matlab中的LMI工具箱求解，所以本研究應用常見處理不確定項的方法，將其轉化成如下形式。定理2給出了處理不確定項Δ(K)的具體過程。

定理2：給定反饋增益矩陣Κ和標量常數ηm，ηM，如果存在適當維數的對稱正定矩陣P>0，Ti>0，Mi>0(i=1,2)和普通矩陣S，N以及變量εk(k=1,2,3)滿足式(27～28)則閉環控制系統(18)是漸近穩定的。

(27)

(28)

其中：

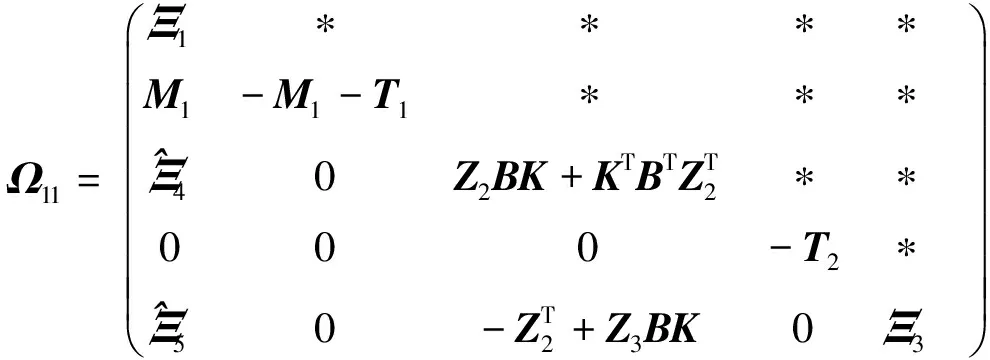
證明：將定理1中的Ω作如下形式改寫：

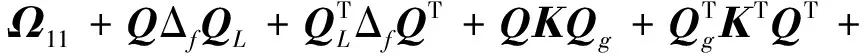
(29)

應用引理3可知，存在εk(k=1,2,3)使得下列不等式成立：

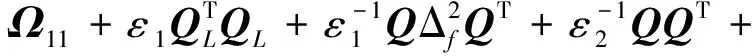
(30)

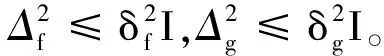
3 控制器設計

根據定理1和定理2，設計狀態反饋控制器使得閉環系統(18)漸近穩定。下面給出量化反饋控制器的設計方法。

(29)

(30)

其中：

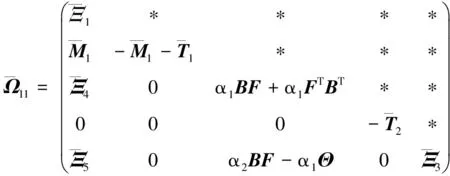
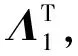
證畢。

注釋2：從定理3中可以看出線性矩陣不等式(29～30)的可行性解不僅與網絡誘導時延的上下界ηM，ηm有關，還與兩個量化器的量化參數δf，δg有關，根據式(11)可知，兩個量化器的量化密度ρf，ρg的大小直接影響線性矩陣不等式(31～32)的求解。

4 數值仿真示例

例1：考慮如下線性系統：

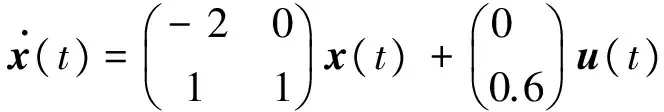
同時選取兩個量化器為對數量化器，并選擇適當的量化密度，根據定理3，取常數α1=9.6，α2=8.0，對應有不同的量化密度ρf和ρg。

在不同的量化密度下，系統的相關參數如表1所示。

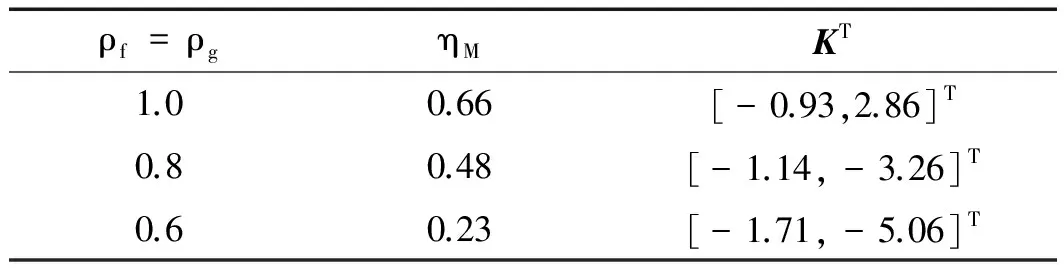
表1 不同量化密度下系統的相關參數比較

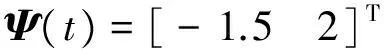
3種量化密度下系統的狀態響應如圖3所示。

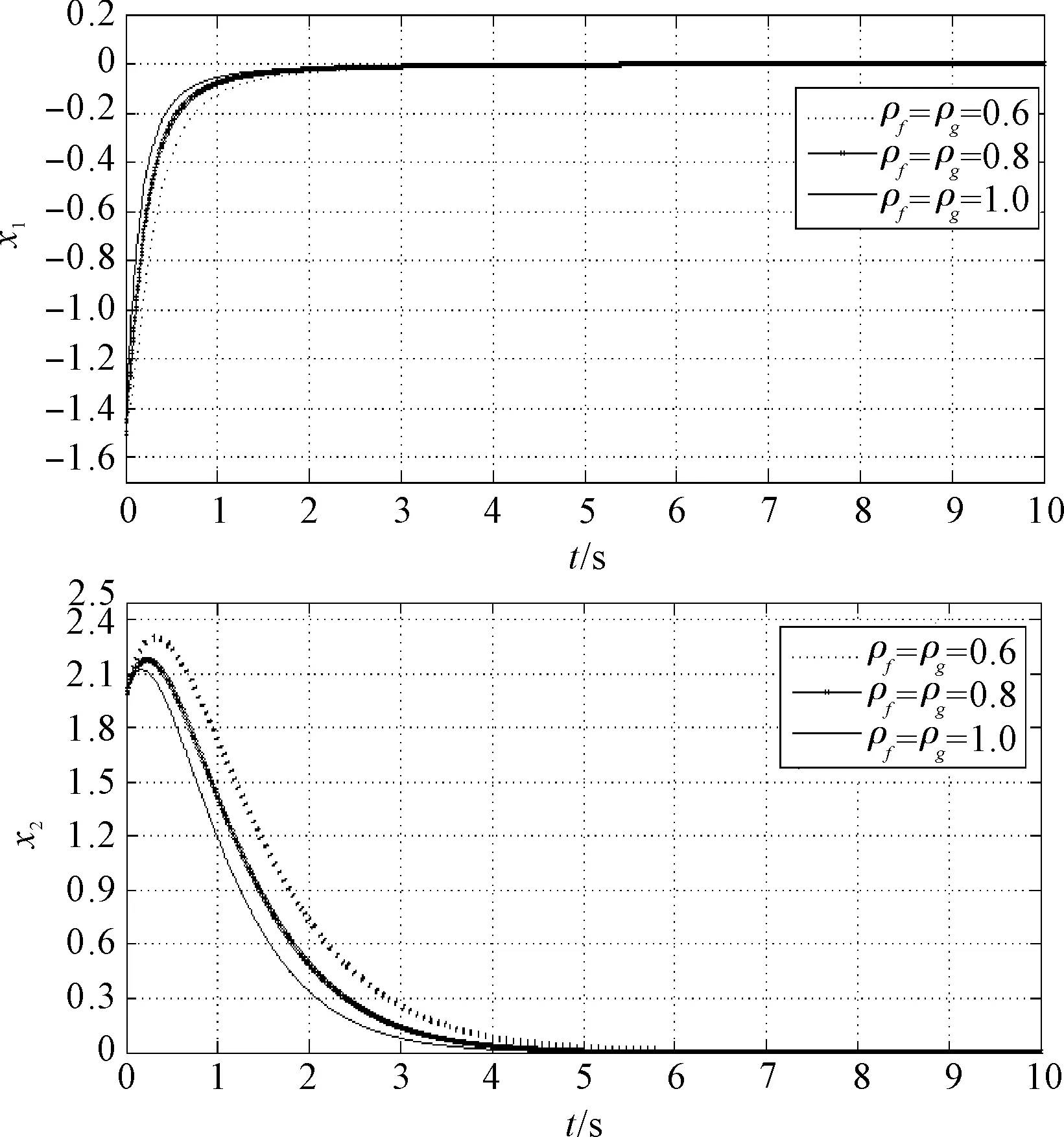
圖3 3種量化密度下系統的狀態響應

從圖3可以看出：(1)通過量化反饋控制器可以使系統漸近穩定；(2)隨著量化器的量化密度增大，量化器對信號的采樣和量化越精細，對系統的信息了解越多，系統到達穩定狀態的時間變短，則系統的控制性能變好。

5 結束語

本研究運用Lyapunov穩定性理論提出了一種基于時變時延依賴的Lyapunov-Krasovskii泛函，并得到了以兩個線性矩陣不等式(LMIs)表示的穩定性判據；在不考慮外部干擾的情況下，設計了量化狀態反饋控制器使得系統漸近穩定，并且得到系統的控制性能與量化器的量化密度ρf和ρg密切相關；最后給出的數值仿真示例驗證了所提方法的有效性。

[1] 游科友，謝立華.網絡控制系統的最新研究綜述[J].自動化學報，2013，39(2)：101-118.

[2] LI H B, YANG H J, SUN F C, et al. A network-bound-dependent stabilization method of networked control systems[J].Automatica,2013,49(8):2561-2566.

[3] XIE D, CHEN X, LV L, et al. Asymptotical stabilisability of networked control systems: time-delay switched system approach[J].IETControlTheoryandApplications,2008,2(9):743-751.

[4] ZHANG L Q, SHI Y, CHEN T W, et al. A new method for stabilization of networked control systems with random delays[J].IEEETransactionsonAutomaticControl,2005,50(8):1177-1181.

[5] ZHANG W A, YU L, YIN S. A switched system approach to H∞control of networked control systems with time-varying delays[J].JournaloftheFranklinInstitute,2011,348(2):165-178.

[6] ELIA N, MITTER K. Stabilization of linear systems with limited information[J].IEEETransactionsonAutomaticControl,2001,46(9):1384-1400.

[7] QU F L, HU B, GUAN Z H, et al. Quantized stabilization of wireless networked control systems with packet losses[J].ISATransactions,2016,6(4):92-97.

[8] JIANG S, FANG H J. Quantized stabilization of discrete-time systems in a networked environment[J].AppliedMathematicalModelling,2014,38(5-6):1685-1697.

[9] FENG Yu, CHEN Xiang, GU Guo-xiang. Quantized feedback stabilizing control for multiple-input networked systems with multiplicative random noises: a stochastic approach[C]. American Control Conference, Portland: IEEE,2014.

[10] LI F W, SHI P, WANG X C, et al. Fault detection for networked control systems with quantization and Markovian packet dropouts[J].SignalProcessing,2015,111(C):106-112.

[11] LIU T F, JIANG Z P, HILL D J. A sector bound approach to feedback control of nonlinear systems with state quantization[J].Automatica,2012,48(1):145-152.

[12] HAN Qing-long. Absolute stability of time-delay systems with sector-bounded nonlinearity[J].Automatica,2005,41(12):2171-2176.

[13] CAO Y Y, SUN Y X, JAMES L. Delay-dependent robust H∞control for uncertain systems with time-varying delays[J].IEEEProceedings-ControlTheoryandApplications,1998,145(3):338-344.

[14] FU M Y, XIE L H. The sector bound approach to quantized feedback control[J].IEEETransactionsonAutomaticControl,2005,50(11):1698-1711.