風力發電機在不同約束狀態下轉子彎曲模態仿真分析

趙 震，譚 亮，鄒強龍，黃 奕

（江蘇中車電機有限公司，江蘇 大豐 224100）

隨著風電市場的蓬勃發展，風電作為一種清潔能源在發電市場占據一席之地。風力發電機作為發電機機組的重要旋轉部件，其運行的穩定性直接影響整個機組的性能。而發電機運行振動大目前是一種常見故障，已成為影響風力發電機機組整體性能的重要因素[1]。

機械結構動態設計分為結構振動特性設計和結構振動響應設計，結構模態分析是結構振動特性設計的核心，多自由度系統振動時，同時又多階模態存在，每階振動模態可用一組模態參數來確認。通常，模態參數包括固有振動、模態質量、模態剛度和模態阻尼比等，其中最重要的是頻率、振型和阻尼比[2]。模態參數對于改善結構動態特性有著重要意義，對旋轉機械進行模態分析很有必要。因此在設計初期對發電機旋轉部件進行模態仿真分析，避免發電機運行時出現振動方面的問題已經是發電機設計的一個重要環節[3][4]。

本文采用有限元分析法對某款風力發電機轉子彎曲模態進行仿真分析，為進一步研究該類型風力發電機轉子彎曲模態情況及試驗模態提供依據，從而實現設計方案的優化。

1 模型建立[5][6]

圖1 某發電機轉子三維模型

用三維軟件建立實體三維模型，在有限元仿真分析軟件中對三維模型進行網格劃分和材料屬性添加。轉子三維模型如圖1所示。

風力發電機轉子部分主要材料屬性如表1所示。

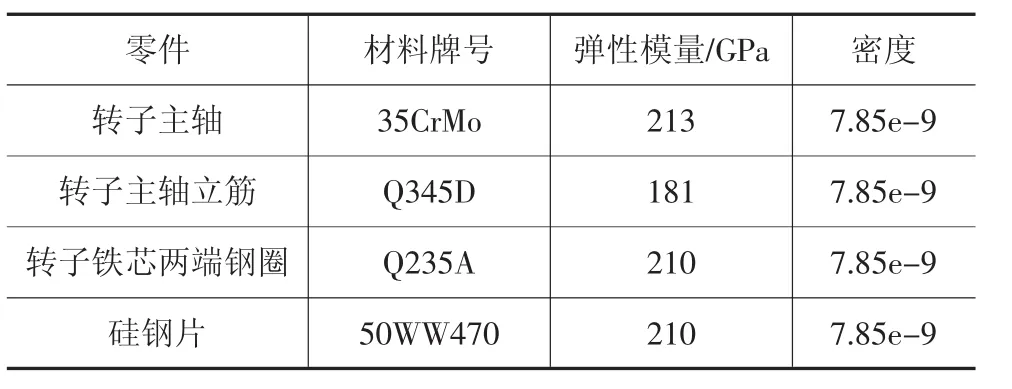
表1 分析采用的材料力學參數

2 模態仿真分析[7][8]

轉子的分析模型采用與實物一致的模型，包括轉子軸、立筋、硅鋼片及通風槽片，線圈質量以質量點的方式布置于硅鋼片的線槽內。

首先對發電機轉子在自由狀態下進行模態分析，其次對發電機轉子有軸承固定時進行模態仿真分析。為了模擬真實轉子的兩端支承，軸承支承系統被簡化為彈簧-阻尼支承，軸承剛度設置，如表2所示，計算所得各主要振型對應頻率如表3所示，自由狀態下轉子振型如圖2所示，軸承固定狀態下轉子振型如圖3所示。

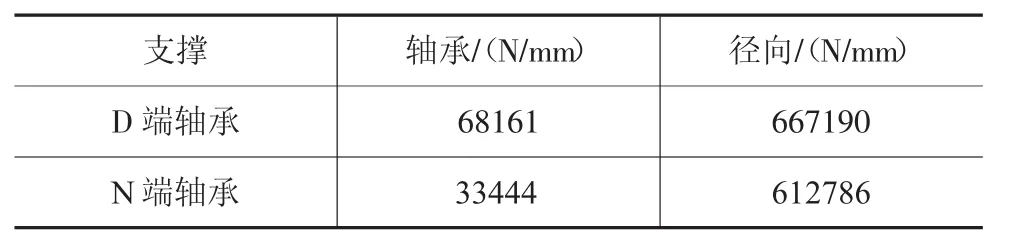
表2 軸承剛度

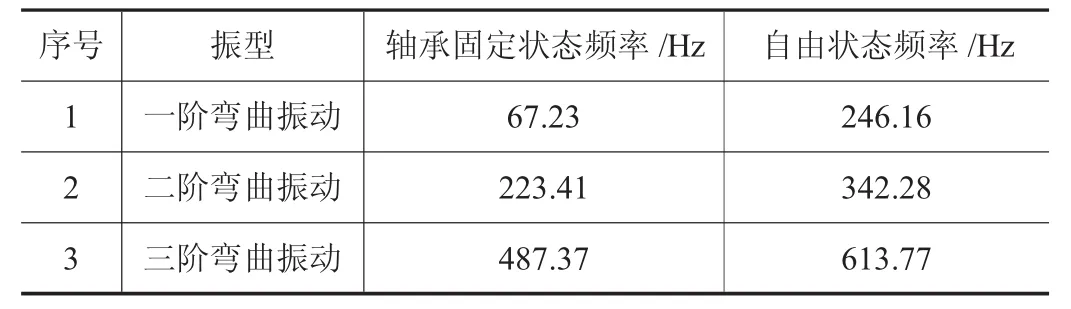
表3 軸承固定狀態下轉子主要振型及頻率值

圖2 轉子在自由狀態下的前四階彎曲振型圖

圖3 轉子在軸承固定狀態下的前三階彎曲振型圖

3 轉子自由狀態下模態測試[9][10]

轉子自由狀態下的模態測試，是將轉子用吊車將兩端吊起，由于繩索是細長彈性體，此種狀態下的轉子類似于自由狀態。試驗采用錘擊激勵方式，根據被測試對象特點，選擇不同數量激勵點，并選取幾個點為參考點，各布置一個傳感器。本次試驗采用細繩將轉子吊起，選用尼龍錘頭對各測點進行敲擊的試驗方式。由于本試驗傳感器數量限制，一般只能體現彎曲振型，無法體現扭轉振型。

試驗檢測的原理是將采集得到的各通道的時域信號濾波后進行FFT變換，可得到頻域信號。如果把系統的激振力f（t）看作輸入，振動的位移響應值x（t）看作輸出，則系統的傳遞函數為：

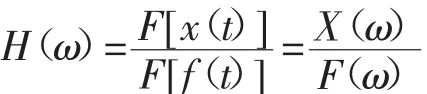
對多自由度系統，其在任意激振力下的運動方程為：

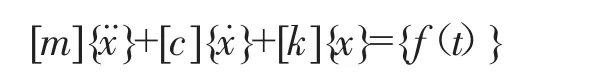
對方程做拉普拉斯變換，并設所有坐標的初始位移和初始速度均為零，則有：

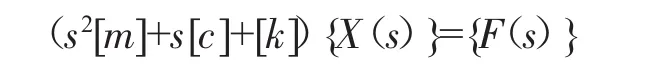
式中：[m]——質量矩陣；

[k]、[c]——系數矩陣；

X（s）、F（s）——分別為x（t）和f（t）的拉普拉斯變換。通過變換可以得到各自由度下的頻響函數。

在頻響函數的基礎上，通過最小二乘法可以得出模態的參數。經對該發電機轉子進行模態試驗，得到該型轉子的固有頻率和振型。試驗結果如表4及圖4所示。

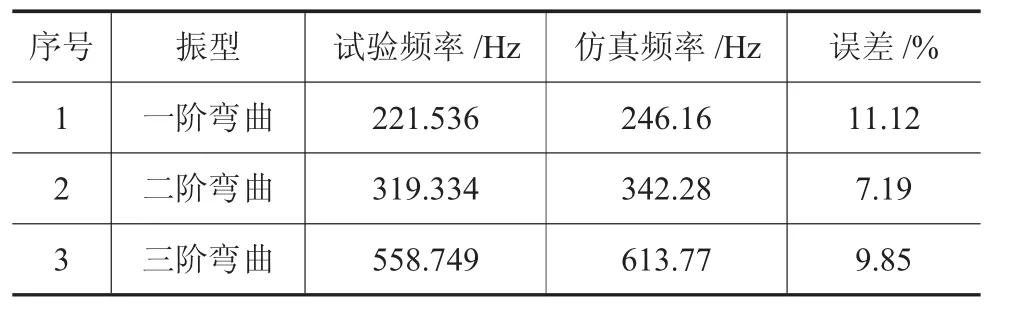
表4 轉子自由狀態下主要振型及頻率值

4 結論

（1）轉子自由模態和在軸承支撐下的模態是有區別的，其受到軸承支撐簡化模型的影響比較大。

圖4 前三階的彎曲振型圖

（2）從試驗結果看，有限元仿真分析與試驗結果還有一定的偏差，主要是由對硅鋼片的處理而致，需要對仿真模型的簡化方式進行深入研究。

[1]李慧新，呂杏梅，等.彈性支撐下風電機組傳動系統結構動力分析[J].動力學與控制學報，2015，13（4）293-294.

[2]馬艷霞，鄧春峰，等.電機聯軸控制的旋轉機械定轉子模態分析［J］.鍛壓裝備與制造技術，2010，45（2）：107-108.

[3]溫 斌，李書強.基于ADAMS的風電雙饋發電機振動研究[J].機械制造，2017，（1）：71-74.

[4]劉木清.雙饋風力發電機振動故障分析和實例處理［J］.上海大中型電機，2012，（1）：71-75.

[5]薛延華，王志廣，邵 濱，等.齒輪箱箱體結構對其振動模態的影響研究[J].機械傳動，2008，32（6）：107-109.

[6]翁 雷，楊自春，等.某船用發電氣輪機轉子模態及動力學分析[J].艦船科學技術，2014，（3）：62-63.