大跨度四線鐵路車站隧道內輪廓研究
卿偉宸,高 楊,章慧健
(1.中鐵二院工程集團有限責任公司,成都 610031; 2.西南交通大學,成都 610031)
1 概述
隨著我國經濟和社會的高速發展,進入21世紀后,我國鐵路建設進入一個新時代。隨著高速鐵路建設在西部山區的不斷開展,隧道建設也開始向“多、長、大、深”方向發展[1-4]。由于西部地區地形復雜、地質艱險,橋隧比重大,大部分鐵路隧線比達到50%以上,部分鐵路如成都至九寨溝鐵路隧線比達90%以上。諸如大瑞線、成蘭線(成都至九寨溝鐵路)部分地段地形條件限制,導致車站伸入隧道內,由于之前國內外無修建四線車站隧道的成功先例,傳統車站設計一般采用Y字形“2+2”、分修式“2+2”、縱列式“3+3”等形式,以控制隧道跨度不超過三線,但上述方案惡化了車站功能,不利于運營管理。顯然,隨著高速鐵路在西部山區的高速發展,傳統的大跨度三線隧道已不能滿足山區選線及設站的需要,四線車站隧道將不可避免越來越多。而四線車站隧道的成功修建和大量采用使得山區車站布置形式更為靈活,車站功能更易得到保證,有利于車站的運營管理;從而有效降低山區鐵路車站設置對線路選線的影響,提高艱險山區雙線鐵路特別是客運專線選線的自由度。
建國以來尤其是20世紀90年代,經過歷代隧道工程技術人員的探索實踐,大跨度三線及以下的車站隧道設計、施工技術已較為成熟,但特大跨度四線車站隧道設計、施工尚無先例。對于特大跨度四線隧道,其開挖面積大、跨度大,為提高隧道空間的利用率、降低工程成本,與高跨比較大的單線隧道、近于圓形的雙線隧道及三線隧道相比,其斷面形式將更加扁平,在力學行為上有較大差別,在結構選型設計中應考慮以下問題。
(1)對特大跨度四線隧道,增大高跨比對提高結構安全性能是有利的[5],但會造成浪費;相反,降低高跨比會提高經濟效益[6],但斷面越扁平,開挖后的應力集中程度增加[7]、應力重分布更加惡化[8-9],增加了隧道工程設計和施工的難度,即隧道開挖后圍巖拱部土體在自重應力場作用下向洞內移動,并導致兩側土體受壓,反映在洞周位移上,拱頂下沉要遠大于水平收斂位移[1]。顯然,支護結構的破壞形態與隧道高跨比有關[6]。
(2)在滿足建筑限界及相關作業要求條件下,在技術可行、經濟合理的范圍內,通過對特大跨度四線隧道洞室的圍巖力學特性,襯砌結構的承載力,大斷面隧道合理的扁平率等進行研究,以確定經濟合理的斷面形式。
本文依托烏蒙山2號出口四線鐵路車站隧道,根據設計需要,針對以上問題,詳細研究了特大跨度四線隧道不同扁平率的內輪廓對圍巖應力、位移、塑性區及結構性能的力學行為影響,以提出合理的襯砌內輪廓及扁平率范圍。
2 工程概況
烏蒙山2號隧道,為單洞雙線隧道位于六盤水—沾益鐵路貴州省境內,由觀音河右岸進洞,進口里程為DK276+090;終于扒挪塊車站,出口里程為DK288+350,隧道全長12 260 m。最大埋深400余m。設計時速為160 km,通行雙層集裝箱。由于運能需要,隧道出口端扒挪塊車站伸入隧道,DK287+740~DK288+350段形成四線車站隧道,長610 m,洞身主要通過以泥巖、頁巖夾砂巖為主的軟巖地層。圍巖物理力學參數按表1取值,襯砌混凝土的物理力學性能指標如表2所示。

表1 圍巖物理力學參數

表2 襯砌混凝土力學參數
3 隧道建筑限界
3.1 隧道建筑限界擬定考慮的主要因素
列車在隧道中行駛,必須有足夠的空間,隧道建筑限界就是為了保證隧道內各種交通正常進行與安全,而規定的在一定寬度高度范圍內不得有任何障礙物侵入的空間。建筑限界是擬定隧道輪廓線的前提,隧道建筑限界是決定隧道凈空尺寸的依據[10]。因此,隧道建筑限界的確定,對隧道的設計來說至關重要。影響建筑限界的主要因素包括以下方面:(1)機車車輛限界;(2)線別及設計速度;(3)線路展線布置及設站要求;(4)電氣化接觸網懸掛設備布置的要求;(5)隧道內通風、照明、通信、警告信號及色燈信號等附屬設備安裝要求。
3.2 四線隧道建筑限界的擬定
本隧道旅客列車設計行車速度160 km/h并通行雙層集裝箱列車。四線車站隧道“基本建筑限界”系根據相關規范[11-14]的規定,并根據本線技術標準、接觸網和站場專業的技術要求綜合確定。大跨度四線車站段建筑限界如圖1所示。

圖1 烏蒙山2號大跨度四線車站隧道建筑限界(單位:mm)
4 襯砌斷面內輪廓研究
4.1 襯砌內輪廓初步擬定
扁平率是指隧道襯砌內輪廓的高度與其寬度的比值[15],現有的鐵路隧道中,單線隧道扁平率為1.16~1.50;雙線隧道扁平率為0.82~0.95;三線隧道為0.70~0.80。對大跨度隧道,隨著扁平率的減小,可減小洞室開挖量,但開挖后的應力重分布狀態變差[7],對支護結構強度需求必將增加。顯然,扁平率是影響支護結構體系受力及工程投資的一個重要因素。
本隧道襯砌內凈空軌上斷面采用曲墻三心圓拱,在滿足限界基礎上,初步擬定了10種不同扁平率襯砌內輪廓,其拱部半徑分別為900、950、1 000、1 050、1 100、1 150、1 200、1 250、1 300、1 350 cm。各斷面參數如表3所示,圖2僅對其中3種內輪廓示意。

表3 斷面參數
4.2 不同襯砌內輪廓的圍巖力學特性分析
4.2.1 塑性區計算分析
圍巖物理力學參數如表1所示。通過計算,得到上述10種不同扁平率工況的毛洞塑性區分布,選取4種典型工況如圖3所示。各工況的塑性區面積和塑性區高度如表4及圖4所示。

表4 不同扁平率內輪廓毛洞的塑性區比較
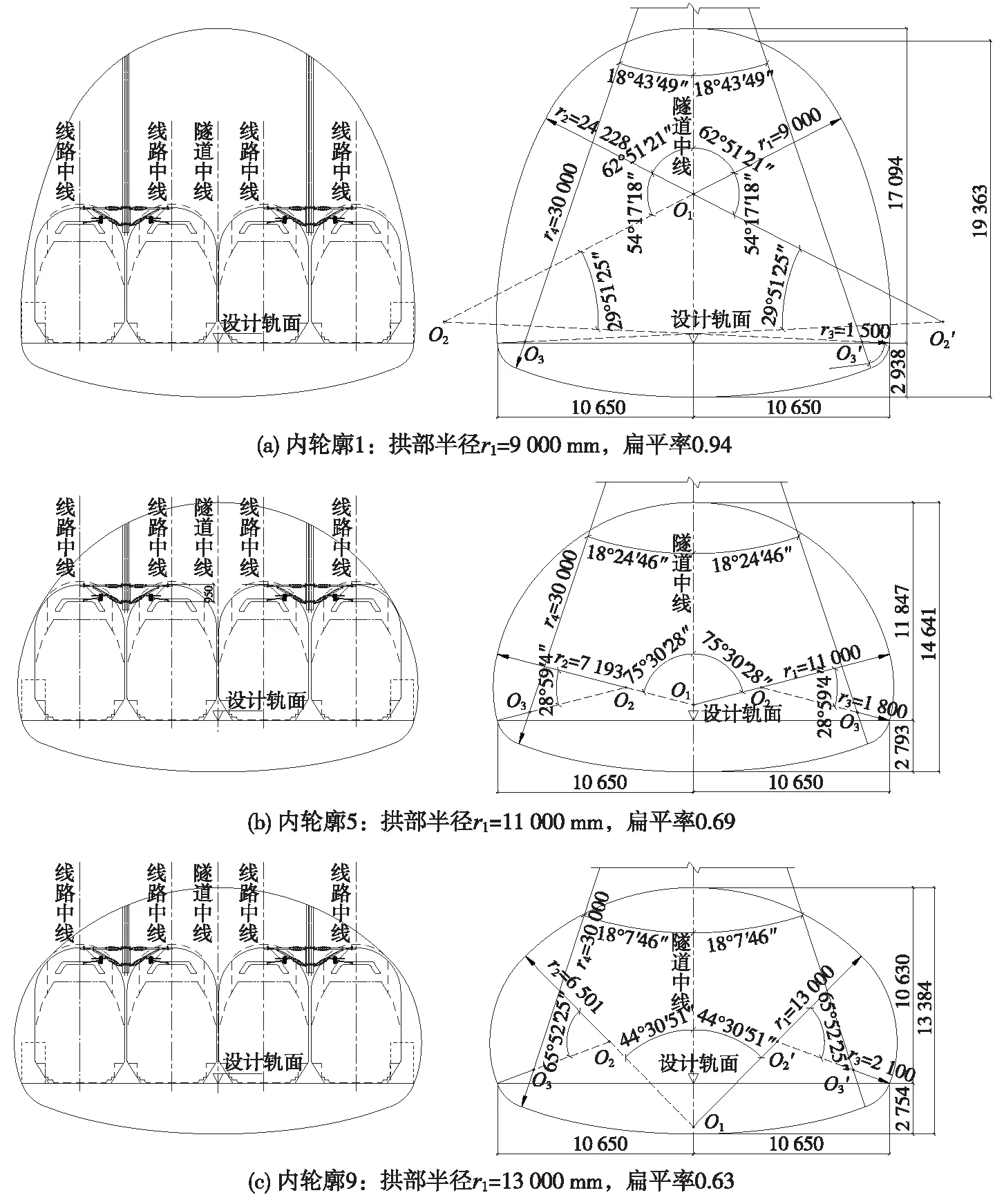
圖2 烏蒙山2號大跨度四線車站隧道內輪廓(單位:mm)

圖3 不同扁平率內輪廓毛洞的塑性區分布形態

圖4 不同扁平率內輪廓毛洞的塑性區
從圖3可以看出,上述10種內輪廓毛洞圍巖塑性區自兩側邊墻底外以一定角度向上發展,拱部塑性區高度約1倍洞徑。
圖4可以看出,扁平率為0.85左右時,拱部塑性區高度最小,但塑性區面積卻并為最小。說明當內輪廓扁平率為0.85左右時,拱部塑性區高度雖然較小,但由于扁平率較大,邊墻部位發生塑性破壞的范圍較大,導致總塑性區面積較大;扁平率為0.69左右時,拱部塑性區高度雖然并不是最小,但塑性區面積相對較小,說明當內輪廓扁平率為0.69左右時,邊墻部位發生塑性破壞的范圍相對較小。綜合毛洞塑性區面積及拱部塑性區高度來看,內輪廓扁平率為0.69左右時較優。
4.2.2 圍巖變形分析
通過數值計算,得到各工況拱頂沉降及水平收斂,整理如表5及圖5所示。
從圖5可以看出,水平收斂與拱頂沉降具有相同的變化趨勢。水平收斂和拱頂沉降隨扁平率的增大先略有減小后急劇增大。當扁平率低于0.69時,水平收斂和拱頂沉降隨扁平率增加總體上略有增加,但變化幅度很小;當扁平率高于0.73時,水平收斂和拱頂沉降隨扁平率增加而急劇增大。由此可見,在特大跨度隧道中,水平收斂起控制作用。當跨度基本一致時,扁平率越大,則洞形越高,邊墻越高且曲率越小,邊墻與仰拱連接曲線曲率變化大,因此水平收斂就越大。水平收斂越大,兩側邊墻向內位移大,導致拱部整體下沉量增大。

表5 不同扁平率內輪廓毛洞圍巖變形比較

圖5 不同扁平率毛洞拱頂沉降收斂
4.3 不同襯砌內輪廓二襯受力分析
4.3.1 安全系數對比分析
根據《鐵路隧道設計規范》[14],混凝土襯砌結構截面安全系數應按下式計算
當e>0.2h時,抗拉安全系數
當e≤0.2h時,抗壓安全系數
式中K——安全系數;
N——軸向力,MN;
ψ——構件的縱向彎曲系數,取ψ=1;
b——截面寬度,m;
h——截面厚度,m;
e0——軸向力偏心距,m;
Rl——混凝土抗拉極限強度,MPa;
Ra——混凝土抗壓極限強度,MPa;
α——軸向力的偏心距影響系數。
對上述10種不同扁平率的內輪廓,均取襯砌厚度為90 cm,按V級深埋條件計算,得到各襯砌拱頂、拱腳、邊墻底及仰拱中部節點的內力并計算出安全系數,具體詳見表6及圖6。

表6 不同扁平率內輪廓襯砌安全系數對比
注:r1為襯砌內輪廓拱部半徑;K為安全系數。

圖6 不同扁平率內輪廓襯砌安全系數對比
結合表6及圖6可知,隨著內輪廓扁平率的減小,拱部圓弧半徑增大,襯砌拱頂、拱腳及仰拱中部截面安全系數減小,邊墻底截面安全系數增大。
從圖6可以很直觀地看出,當扁平率位于0.67~0.70時,襯砌結構受力更為均衡。
4.3.2 襯砌內力計算
對4.1節中10種不同扁平率的內輪廓,取襯砌厚度為90 cm,按V級圍巖深埋條件計算,各襯砌拱頂、拱腳、邊墻中部、邊墻底及仰拱部位截面內力及配筋量分別如圖7、圖8所示。

圖7 不同扁平率內輪廓襯砌截面內力

圖8 不同扁平率內輪廓襯砌截面配筋量
從圖7及圖8可以看出,隨著扁平率減小,拱頂及拱腳部位截面彎矩增大,軸力增大,需求配筋量增大;隨著扁平率減小,邊墻底截面彎矩減小,軸力增大,需求配筋量減小。當扁平率位于0.65~0.70時,襯砌截面配筋量較小且沿全環二次襯砌更為均衡。
4.4 不同內輪廓襯砌結構經濟性分析
對4.1節中10種不同扁平率的內輪廓的襯砌結構,結合計算分析,在保證各襯砌結構初期支護及二次襯砌(均采用鋼筋混凝土)最小安全系數基本一致的情況下,擬定的主要支護參數如表7所示。

表7 不同扁平率內輪廓襯砌結構支護參數
同時,為更好地指導特大跨度隧道內輪廓擬定,補充了受力性能更好的圓形內輪廓襯砌結構,主要支護參數如表7所示。
通過對表7中11種不同內輪廓的襯砌結構工程造價進行計算,對比分析結果詳見圖9。從圖9可以看出:(1)襯砌5總造價最低;(2)對采用圓形內輪廓的襯砌結構,二襯圬工及鋼筋均較節省,但由于開挖、初期支護等工程量大幅增加,工程造價并沒有明顯優勢;(3)從內輪廓扁平率與襯砌工程造價關系來看,當內輪廓扁平率在0.67~0.86范圍,相對較省。

圖9 不同扁平率內輪廓襯砌結構工程造價
5 結論
對大跨度扁平隧道,扁平率是影響隧道結構受力的一個主要因素。結合烏蒙山2號四線車站隧道實際工程,通過數值模擬及綜合比較分析,對大跨度四線隧道合理扁平率范圍開展了深入研究,得出如下主要結論。
(1)對擬定的10種內輪廓毛洞進行分析,其圍巖塑性區為自兩側邊墻底外以一定角度向上發展,拱部塑性區高度約1倍洞徑。綜合毛洞塑性區面積及拱部塑性區高度來看,內輪廓扁平率為0.69左右時較優。
(2)水平收斂和拱頂沉降隨扁平率的增大先略有減小后急劇增大。當扁平率低于0.69時,水平收斂和拱頂沉降隨扁平率增加總體上略有增加,但變化幅度很小;當扁平率高于0.73時,水平收斂和拱頂沉降隨扁平率增加而急劇增大。由此可見,在特大跨度隧道中,水平收斂與拱頂沉降具有相同的變化趨勢,且水平收斂起控制作用。究其原因,當跨度基本一致時,扁平率越大,洞形越高,邊墻越高且曲率越小,邊墻與仰拱連接曲線曲率變化大,水平收斂就越大。水平收斂越大,兩側邊墻向內位移大,導致拱部整體下沉量增大。
(3)隨著內輪廓扁平率的減小,拱頂圍巖應力松弛嚴重,造成拱頂下沉和仰拱突起變形比較嚴重,拱腳及邊墻上部受到強烈擠壓,造成壓應力集中嚴重,從而導致拱頂、拱腳及仰拱部位安全系數減小;另一方面,隨著內輪廓扁平率的減小,邊墻底與仰拱連接更為圓順平緩,應力集中減小,邊墻底安全系數增大。結合襯砌結構各部位安全系數變化趨勢,當扁平率位于0.67~0.70時,襯砌結構受力更為均衡。
(4)隨著內輪廓扁平率減小,二次襯砌拱頂及拱腳部位截面需求配筋量增大,邊墻底截面配筋需求量減小。當扁平率位于0.67~0.70時,襯砌截面配筋量較小且沿全環襯砌更為均衡。
(5)襯砌結構工程造價基本上呈現“隨著內輪廓扁平率增大,先減小后增大”的趨勢,當內輪廓扁平率在0.67~0.86時,相對較省,襯砌結構采用受力性能更好的圓形內輪廓,工程造價并沒有優勢。
綜合考慮洞室穩定性、洞周位移、塑性區、圍巖應力、結構內力及工程造價,大跨度四線鐵路隧道合理的偏平率應控制在0.67~0.70。
[1] 關寶樹.隧道施工的技術特性、理念及其發展[J].鐵道建筑技術,2003(4):1-5.
[2] 孫鈞.山嶺隧道工程的技術進步[J].西部探礦工程,2000(1):1-6.
[3] 王夢恕.交通建設進入隧道時代[J].建設科技,2004(7):26-27.
[4] 王建宇.隧道工程和地下空間開發在可持續發展中的地位[J].世界隧道,1996,3(6):1-3.
[5] 何復生.礦山法隧道施工期洞室圍巖安全性評價[J].鐵道標準設計,2012(4):104-107.
[6] 蔣樹屏,黃倫海,胡學兵.超大斷面公路隧道的設計與研究[J].地下空間與工程學報,2005,2(1):54-61.
[7] 顧洪源.大斷面小凈距隧道斷面優化及其設計參數研究[J].鐵道標準設計,2013(2):85-89.
[8] 關寶樹.隧道工程施工要點集[M].北京:人民交通出版社,2003.
[9] 袁小龍.基于應變軟化模型的扁平大跨度隧道開挖過程穩定性分析[D].鄭州:鄭州大學,2012:Ⅰ-Ⅱ.
[10] 劉婷,王智慧,賀桂超.一種公路隧道結構斷面優化與設計方法[J].中國高新技術企業,2008(14):180-181.
[11] 中國鐵路總公司.鐵路技術管理規程[S].北京:中國鐵道出版社,2014.
[12] 中華人民共和國鐵道部.鐵建設[2003]76號 新建客貨共線鐵路設計暫行規定[S].北京:中國鐵道出版社,2003.
[13] 中華人民共和國鐵道部.鐵科技函[2004]157號 鐵路雙層集裝箱運輸裝載限界(暫行)[S].北京:中國鐵道出版社,2004.
[14] 中華人民共和國鐵道部.TB10003—2005 鐵路隧道設計規范[S].北京:中國鐵道出版社,2005.
[15] 曾宜江.單拱四車道公路隧道結構優化的研究[D].長沙:中南大學,2009:26-27.

