基于改進多輸出支持向量機的聲發射源定位研究*

朱 軍，史 勃，張環宇，榮勝波，黃益澤

(中國科學院 沈陽自動化研究所，遼寧 沈陽 110000)

0 引 言

聲發射(acoustic emission，AE)現象[1]的活動性能夠表征煤巖體受載、變形及破壞的狀態及發展過程。故聲發射監測可以預測煤與瓦斯突出點的位置[2]，AE源的定位對于煤巖體破裂情況的分析具有重要意義。傳統的定位方法大多基于AE速度和時間的一些算法如時差定位法[3]、模態AE定位[4]以及能量定位[5]。而煤礦生產環境復雜，為了提高定位的準確性，出現了基于統計學習理論的定位方法[6]和基于特征匹配的算法[7,8]，如神經網絡、支持向量機(support vector machine,SVM)、加權K均值算法等[9]，其中，SVM的定位精度相比于神經網絡有了更大的提升[10]，所需采集的樣本也相對較少，但其參數調節比較困難。

為了改善AE定位的效果，結合核主成分分析(kernel principal component analysis,KPCA)提出了一種改進的多輸出最小二乘SVM(least squares SVM,LSSVM)的定位算法(KPCA-LSSVM)。采用KPCA對采集信息進行處理，提取多路信號中對應時間延遲的特征，采用多輸出LSSVM對特征向量與位置信息之間的關系進行擬合，得到對應的AE源位置,將該方法應用于煤礦瓦斯突出災害的預測，仿真試驗結果表明：本文方法能夠獲得更高精度的定位結果，提高了定位效率。

1 KPCA-LSSVM定位算法

1.1 KPCA

KPCA的處理過程如下：

k(xi,xj)=φT(xi)φ(xj)

(1)

其中，假定已經進行了數據預處理過程，使得訓練樣本的所有特征向量滿足零均值條件，即

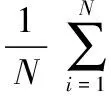
(2)

2)求解特征子空間坐標

Kα=λα

(3)

式中λ為K的特征值；α為對應的子空間基向量。

3)特征向量的選取

計算投影

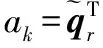
(4)

式中ar,j為基向量αr的第j個元素。

1.2 多輸出SVM回歸

多輸出SVM回歸是針對系統回歸函數的因變量y(為一個向量，即y∈Rk,k>1)而提出的一種新的SVM算法，圖1為定位模型框圖，用定義在超球上的損失函數代替定義在超立方體上的損失函數，損失函數如下

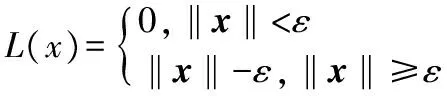
(5)

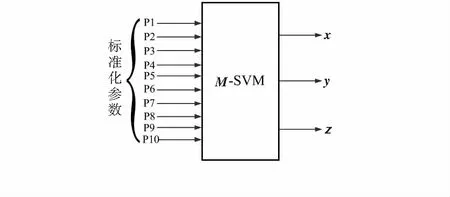
圖1 多輸出SVM定位模型

對于M維輸入，N維輸出的函數擬合問題，設訓練樣本集

{(xi,yi)},i=1,2,…,L,xi∈RM,yi∈RN

可以構造回歸函數

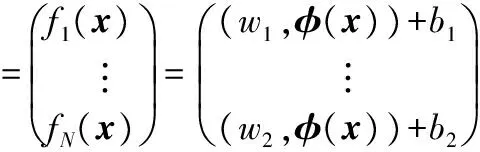
=(W,φ(x))+B

(6)

式中W=(w1,w2,…,wN);B=(b1,b2,…,bN)。該回歸問題等價于不等式約束下的極值問題

(7)

式中ui=‖ei‖,ei=yi-(W,φ(xi))+B。根據KKT條件及對偶原理，上述問題轉化為求極值問題

(8)

為了求取上述函數的極值，分別對wi,bi,ui,αi求偏導數并令偏導值等于0,即

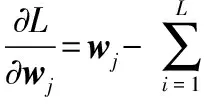
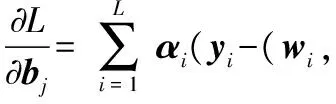
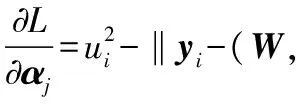
(9)

可得到

(10)

(11)

式中Φ=[φ(x1),…，φ(xL))]T,Dα=diag{α1,…,αL},A=[α1,…,αL]T,I=[1,…，1]T。

相比單維輸出情況下的最優化問題要該求極值問題更復雜，應采用特殊的迭代法求解，操作方法如下：

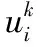
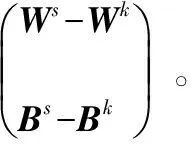
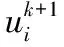
1.3 文化基因優化算法

為了避免前述算法落入局部最優，采用文化基因算法(memetic algorithm,MA)進行改進，將局域搜索和遺傳算法相結合，兼顧了局部搜索算法的深度優勢和群體算法搜索面積大的優點 ，交叉和變異運算如下

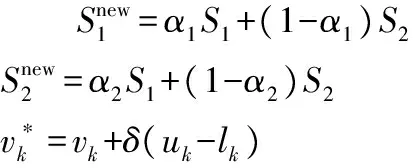
(12)

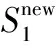
SVM的準確度依賴于學習機外部參數，針對最優參數確定的問題，MA使用的SVM外部參數有C和ε，根據適應度從變異后的種群中選擇G個新個體作為下一代，本文選用均方差作為適應度函數，其表達式如下

(13)

2 試驗平臺與AE信號的產生

AE試驗平臺如圖2所示。采集AE信號如圖3所示。選取振鈴計數、事件計數、幅度、能量計數、上升時間、持續時間、有效值電壓和平均值電壓8個參數，試驗平臺為5路傳感器信號，故生成了維度為40的輸入向量。

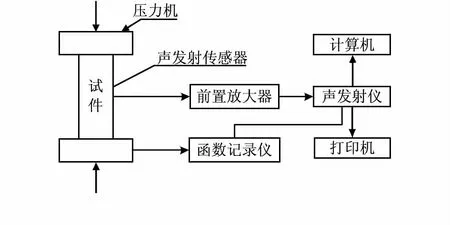
圖2 AE試驗平臺示意

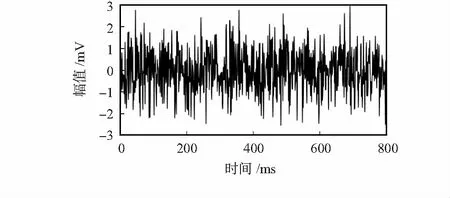
圖3 典型的連續型AE信號

3 試驗結果與分析

基于KPCA-LSSVM的AE定位算法的框架如圖4。

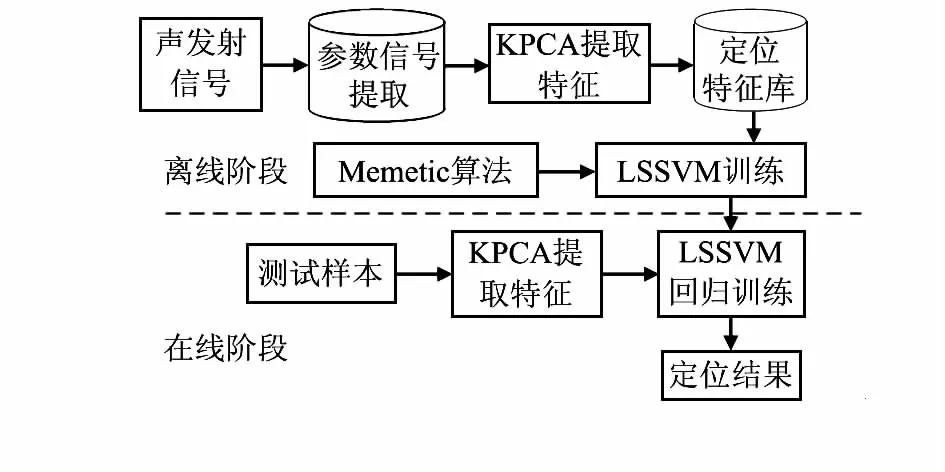
圖4 KPCA-LSSVM算法框架

每次采集數據并生成一個40維的輸入向量，在離線階段收集多組數據，首先進行歸一化處理，KPCA中選擇高斯徑向基和函數。對式(2)的求解，采用奇異值分解(singular value decomposition,SVD)方法。試驗發現，當σ2=1 900時，特征提取的效果比較好，前10個特征參數的貢獻率之和超過95 %，因而輸入向量由40維變為10維。其前20個特征的貢獻率分布如圖5所示。

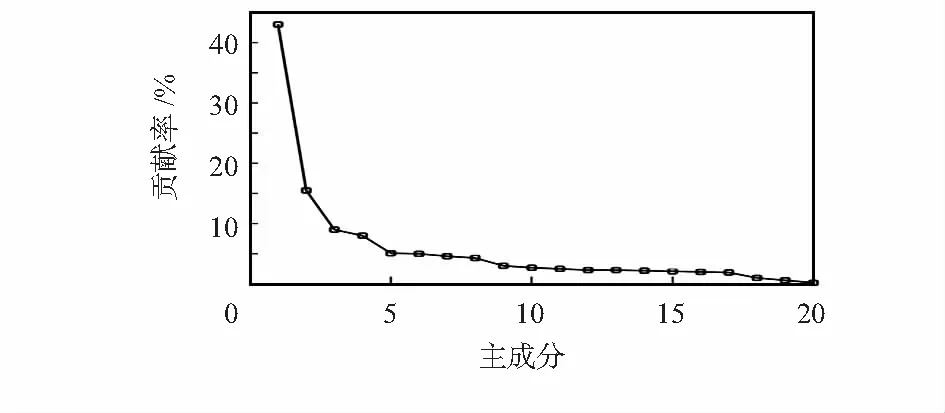
圖5 核矩陣中前20個成分的貢獻率

為了驗證算法的性能，在一次試驗中，采集了100組離線數據，通過訓練并在線測試了一些AE點。結果如表1。

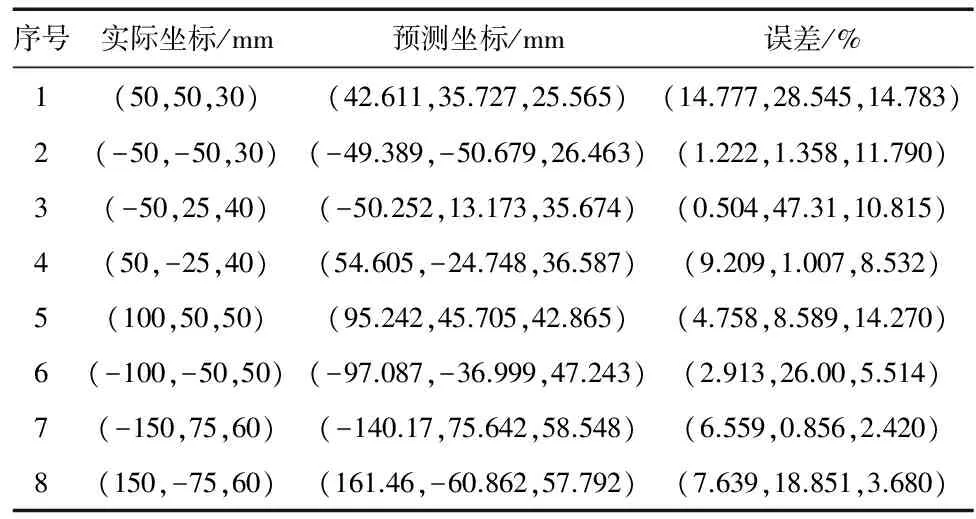
表1 定位結果

為了驗證KPCA-LSSVM的AE定位優越性，與傳統的PCA-LSSVM(手動方式確定LSSVM參數)、PCA-GA-LSSVM(GA算法優化LSSVM參數)進行對比測試，采用定位誤差和平均定位誤差對AE定位結果進行評價，公式為

(14)

(15)

式中n為測試點的數量。

采用LSSVM擬合特征向量與地理位置信息之間的關系時，參數C和ε的選擇至關重要，采用PCA-LSSVM和PCA-GA-LSSVM以及KPCA- LSSVM進行定位試驗，參數如表1所示。定位比較結果如圖6所示，可以得出：相比于其他兩種方法，KPCA-LSSVM的定位精度有一定程度的提高，因為GA，MA算法可以找到更加合理的LSSVM參數C和ε的值，建立的LSSVM可以更好擬合特征向量與位置信息之間的映射關系，定位結果更加可靠。

為了比較各種方法進行AE定位的訓練速度，仿真統計PCA-LSSVM、PCA-GA-LSSVM和KPCA -LSSVM的運行時間，結果如表2。從訓練結果可知：PCA-LSSVM最快，減少了尋優的過程，但是其設置參數無法準尋一定的規律，

具有經驗性，其定位精度也無法保障，沒有普遍適用性，而KPCA-LSSVM的訓練效率要高于PCA-GA-LSSVM,定位的實時性更優，更符合AE定位的要求。

4 結 論

針對煤礦中煤與瓦斯突出災害，提出了一種基于KPCA-LSSVM的AE定位算法，該算法采用KPCA提取聲發射參數信息中對定位結果貢獻重要的特征，對數據進行一定的降維壓縮，從而降低了LSSVM的復雜度，最后采用LSSVM擬合特征與位置信息的非線性關系，并采用Memetic算法搜索LSSVM的最優參數，試驗結果表明：KPCA-LSSVM的定位精度要高于傳統算法，并且運行時間相比同級別算法更具優勢。

[1] 曾憲濤,姜耀東,王宏偉,等.單軸壓縮條件下煤巖體聲發射特性研究[J].煤炭工程,2015,47(2):75-77.

[2] 涂慶毅,程遠平,王 亮,等.煤與瓦斯突出的動態過程研究[J].煤炭科學技術,2015,43(6):71-75.

[3] 于 洋,王 賽.一種新的聲發射時差定位方法[J].化工自動化及儀表,2015,42(10):1127-1130.

[4] 張維剛,李凱麗,肉孜麥麥提,等.金屬薄板中導波的模態識別和波速測定[J].聲學技術,2015(4):322-326.

[5] 劉艷芳,張會芝,王鮮芳.改進的基于能量的聲源定位算法[J].計算機工程與設計,2015(7):1976-1980.

[6] 蔡朝暉,夏 溪,胡 波,等.室內信號強度指紋定位算法改進[J].計算機科學,2014,41(11):178-181.

[7] 馬 豪,尹健龍,李東升.基于小波分解的磨床聲發射特征信號提取方法[J].傳感器與微系統,2016,35(7):13-15.

[8] 張會清,石曉偉,鄧貴華,等.基于BP神經網絡和泰勒級數的室內定位算法研究[J].電子學報,2012,40(9):1876-1879.

[9] Van Laarhoven T,Marchiori E.Local network community detection with continuous optimization of conductance and weighted kernel K-means[J].Journal of Machine Learning Research,2016,17(1):5148-5175.

[10] Ghamisi P,Couceiro M S,Benediktsson J A.A novel feature selection approach based on FODPSO and SVM[J].IEEE Transactions on Geoscience & Remote Sensing,2015,53(5):2935-2947.