基于牛頓梯度優化的彈性多核學習*

何佳佳，陳秀宏，田 進，萬 月

(江南大學 數字媒體學院，江蘇 無錫 214122)

0 引 言

多核學習(multiple kernel learning，MKL)[1]是機器學習領域的熱門研究課題，已成功應用于生物信息學[2]、計算機視覺[3]、數據挖掘等方向。與利用單一核的核方法相比，MKL通過組合多個基本核函數代替單一核函數，使得核函數的應用更為靈活；由于其不依賴樣本數據，故具有更強的可解釋性和可擴展性。

本文提出了一種基于牛頓梯度優化方法的彈性MKL (Newton gradient optimization method for elastic MKL，NO-EMKL)算法，根據彈性理論，將混合范數作為正則化項加入目標函數，使得MKL在實現自適應目的的同時能平衡解的稀疏性，采用二階牛頓梯度下降法提高MKL的效率。結果表明:以上方法能計算多核學習的黑塞(Hessian)矩陣，獲得的下降方向比快速下降法更好，進一步減少了算法的迭代次數。

1 MKL框架

給定數據集{(xi,yi)}ni=1，xi∈χ，χ為輸入空間；yi表示數據xi的標簽，對二分類問題，yi∈{+1,-1}。核方法通過映射φ:χ→h將數據變換到Hilbert空間h中，核函數定義為h中的內積，表明可通過核函數k(x,z)隱式地計算映射函數φ在h中的內積k(x,z)=〈φ(x),φ(z)〉，避免了維數災難。在MKL中，核函數通常表示為多個基本核函數的加權相加或相乘。

根據Bach分塊理論[4]，MKL即為尋找以下問題的最優解

w.r.t.ω=(ω1,…,ωM)∈Rk1×…×RkM,

?i∈{1,…,n}

(1)

MKL的決策函數為

f(z)=〈ω,z〉+b

(2)

式中μm為核函數的加權系數，可通過求解問題(1)的對偶形式獲得。MKL分塊階段的l1范數將導致ω的稀疏性。

2 NO-EMKL

2.1 EMKL

多元線性回歸的Lasso模型為

(3)

式中 ‖·‖為l2范數;‖·‖為l1范數。目標函數(3)第二項為正則化項，用來控制參數的稀疏性。Zou H等人[5]將式(3)中的正則項用混合范數代替以達到自適應調整稀疏性的目的，即考慮以下彈性優化模型

(4)

該模型通過正則化參數(λn,μn)調節l1范數項和l2范數項。

根據l1范數項的變分公式[6,7]，并引入混合范數的正則項的彈性思想，得到以下EMKL模型

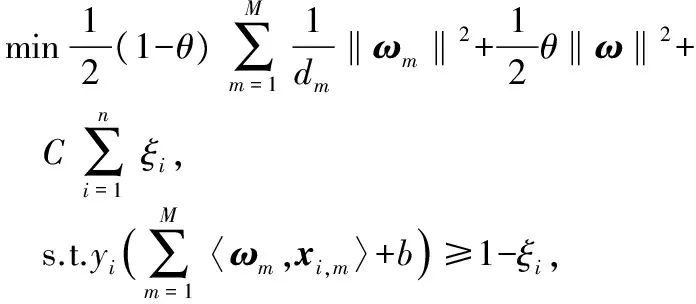
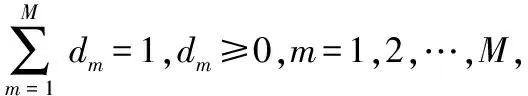
ω=(ω1,…,ωM)∈Rk1×…×RkM,

ξi∈Rn,b∈R

(5)

式中θ為變量,0<θ<1,用于平衡稀疏性。

2.2 EMKL的牛頓梯度法

本文EMKL框架考慮的合成核K(xi,xj)是一些基本核km(xi,xj)的線性組合

(6)

(7)

(8)

(9)

文獻[6]指出，僅需用簡單的梯度下降法即可解決該凸優化問題，且收斂較快。本文在快速梯度下降的基礎上引入二階牛頓優化來求解問題(9)以進一步提高收斂速度。

記問題(7)的目標函數為J(α,d)，對d和α使用交替法求解。對于給定的d，式(7)即為標準SVM式(8)，設其解為α*，相應的支持向量集為sv；求解式(9)，計算J(α*,d)關于d的梯度

(10)

為了獲得二階信息，在對gm求導時需計算?α*/?dm。由于所有支持向量均處于最大間隔邊界面上[9]，故有

(11)

(12)

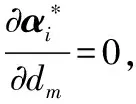
(13)

(14)

(15)

(16)

約束項保證了任何解都落在區間[d,d+s]中，從而滿足原始約束式(9)。

3 實驗與結果分析

為了驗證本文NO-EMKL方法的有效性，與標準核SVM和基于快速梯度下降法的Simple MKL進行了實驗比較。

3.1 參數設置和實驗數據

Simple MKL和NO-EMKL實驗中所使用的基本核函數包括：10個高斯核函數，其帶寬σ,分別取0.5，1，2，5，7，10，12，15，17，20；3個多項式核函數，其中a=1，指數b的取值分別為1，2，3。對每個基本核函數分別計算核矩陣。通常核SVM中用到的單核為高斯核函數，其帶寬σ取10；超參數C=100。本文討論的是二分類問題，選取加州大學歐文分校提供的標準測試數據集(University of California,Irvine,UCI)中8種2類別數據集進行實驗，這些數據集的構成如表1所示。

表1 UCI數據集

3.2 正則項參數θ選取

根據本文NO-EMKL算法，采用5折交叉驗證的方法為表2中的8個UCI數據集分別選取合適的正則項參數θ。θ的取值分別為{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9}；將每個數據集中的樣本數據分別分成5組，輪流將其中4組作為訓練集而另外1組作為測試集，并分別計算分類精度，取5次實驗結果的均值作為對應θ的分類結果，其對應關系如表2所示。對最高分類精確度進行標粗，如果不同的θ值對應著相同的最高分類精確度，選擇其中一個標粗。

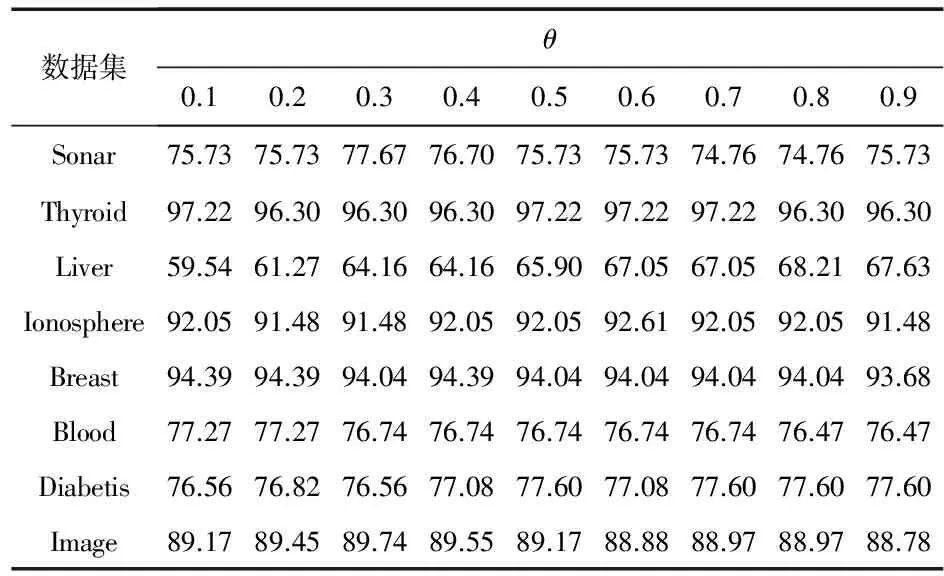
表2 數據分類精確度與θ關系 %

從表2可以看出，不同的θ值影響著NO-EMKL算法的分類精度，且不同數據集的最高分類精度對應的θ值一般也不相同，說明每個數據集均具有最合適的θ值。NO-EMKL算法可以根據數據集調節到最合適的θ值，使模型的分類效果達到最好。

3.3 分類精確度比較

根據表2，分別為8個UCI數據集選取最合適的θ值用于NO-EMKL算法，8個數據集Sonar，Thyroid，Liver，Ionosphere，Breast，Blood，Diabetis及Image對應的θ取值分別為0.3，0.6，0.8，0.6，0.5，0.2，0.7及0.3。隨機選取8個UCI數據集中50 %的數據作為訓練集，剩下的數據作為測試集；訓練數據歸一化為均值0及單位方差的數據，測試數據使用訓練數據的均值和方差進行歸一化。每種算法在每個數據集上運行10次求平均；對于Simple MKL和NO-EMKL，選擇對偶間隙小于0.01或迭代次數大于500次作為終止條件；最后得到的3種算法對數據集的平均分類精度如表3所示，對分類精度最高的數據進行標粗。

表3 3種算法的分類精度比較 %

從表3中可以看出，單核的SVM分類結果較差，本文提出的NO-EMKL算法在大部分的數據集上(除了數據集Diabetis)相較其他兩種算法有較好的分類精度，Simple MKL的分類結果處于兩者之間。

3.4 迭代次數比較

Simple MKL和NO-EMKL在8個數據集上進行實驗，并比較當達到停止迭代條件時迭代次數和對偶間隙的關系，如圖1所示。可以看出：在開始階段，Simple MKL的對偶間隙較NO-EMKL算法下降快，但是接近最優解時，收斂速度明顯低于NO-EMKL，甚至出現了振蕩，并導致迭代次數大幅度增加，從而增加了計算成本。由此可見，采用二階牛頓梯度下降法的效果明顯好于快速梯度下法。

圖1 NO-EMKL和 Simple MKL收斂速度

3.5 訓練時間比較

所考慮的訓練時間不包含核矩陣的生成時間。由于標準SVM不需要對核系數進行學習，所以,NO-EMKL和Simple MKL 2種算法在8個數據集上的訓練時間，在各數據集上運行10次后的平均訓練時間如表4所示，正則項參數θ的選取根據表2確定。因此，Simple MKL算法相對于NO-EMKL長，尤其當數據集較大時，訓練時間的差異更明顯，這主要是因為在計算權系數時，兩種方法所采用的梯度下降法不同，導致收斂速度不同，進一步說明了NO-EMKL算法的性能更優。

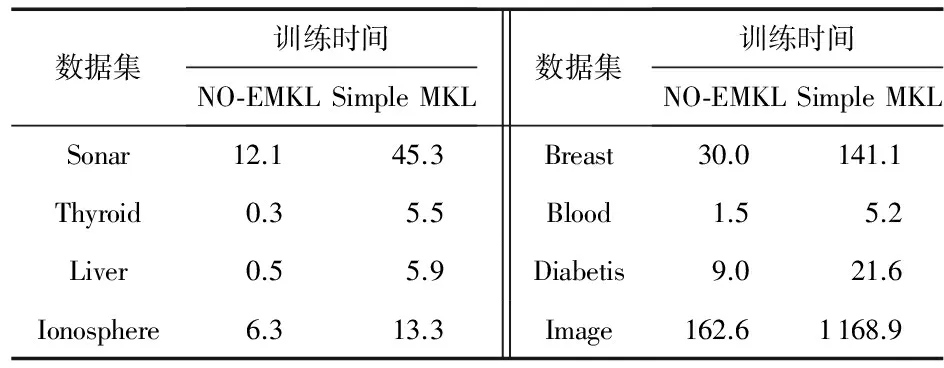
表4 訓練時間 s

4 結束語

針對稀疏多核學習算法在產生權系數和收斂速度上的問題，提出了NO-EMKL算法。該算法根據彈性理論而在目標函數中引入彈性項，使得多個基本核函數能自適應地融合，從而能更好地保留有用信息；而在算法優化階段，算法采用二階牛頓梯度下降法，使算法在更少的迭代次數內即可達到收斂。實驗結果表明：NO-EMKL算法相對于Simple MKL和SVM不僅具有更好的分類精度，還具有較快的收斂速度。

[1] Lanckriet G R G,Cristianini N,Bartlett P,et al.Learning the kernel matrix with semidefinite programming[J].The Journal of Machine Learning Research,2004,5:27-72.

[2] Damoulas T,Girolami M A.Probabilistic multi-class multi-kernel learning:On protein fold recognition and remote homology detection[J].Bioinformatics,2008,24(10):1264-1270.

[3] Duan L,Tsang I W,Xu D,et al.Domain transfer svm for video concept detection[C]∥IEEE Conference on Computer Vision and Pattern Recognition,2009:1375-1381.

[4] Bach F R,Lanckriet G R G,Jordan M I.Multiple kernel lear-ning,conic duality,and the SMO algorithm[C]∥Proceedings of the twenty-first International Conference on Machine Learning,ACM,2004:6.

[5] Zou H,Hastie T.Regularization and variable selection via the elastic net[J].Journal of the Royal Statistical Society:Series B(Sta-tistical Methodology),2005,67(2):301-320.

[6] Alain R,Francis R B,Phane C,et al.Simple MKL[J].Journal of Machine Learning Research,2008,9:2491-2521.

[7] Sch?lkopf B,Smola A J.Learning with kernels:Support vector machines,regularization, optimization,and beyond[M].Boston:MIT Press,2002.

[8] Bousquet O,Herrmann D J L.On the complexity of learning[C]∥Advances in Neural Information Processing Systems 15:Procee-dings of the 2002 Conference,MIT Press,2003:415.

[9] Chapelle O,Rakotomamonjy A.Second order optimization of kernel parameters[C]∥Proc of the NIPS Workshop on Kernel Learning:Automatic Selection of Optimal Kernels,2008:87.