無線傳感器網絡中改進的DV-Hop定位算法*

李鳳超，高美鳳

(江南大學 輕工過程先進控制教育部重點實驗室，江蘇 無錫 214122)

0 引 言

目前，無線傳感器網絡節點自定位技術在理論上取得了很大進展，提出了很多定位算法。

距離矢量跳(distance vector hop,DV-Hop)定位算法是一種非測距定位算法，具有復雜度低、可擴展性好等優點[1]，但其定位精度較低，針對這一問題，進行了很多方面的改進和研究，例如：TMCD-DV-Hop算法[2]在傳統DV-Hop定位算法中加入閾值機制進行錨節點篩選，并對平均每跳距離(簡稱平均跳距)進行校正。同一未知節點對不同的錨節點采用不同的平均跳距且利用Quasi-Newton方法對定位結果進行優化[3]。利用RSSI測距技術進行改進，通過將未知節點升級為次錨節點，根據非線性共軛梯度法進行逼近以減小誤差，有效提高了定位精度[4,5]。對未知節點接收到的錨節點平均跳距加權處理以提高精度[6]。文獻[7]使用蝙蝠算法(bat algorithm,BA)對DV-Hop定位的結果進行優化。文獻[8]使用三角形內點測試(approximate point-in-triangulation test,APIT)與DV-Hop相結合以減小定位誤差。上述改進算法存在的問題有：1)需要額外投入硬件成本;2)引入迭代算法增加了時間和能量的消耗，3)重點對錨節點平均跳距的改進而忽略了距離計算時的誤差。

本文在DV-Hop定位算法的基礎之上，通過對錨節點平均跳距、未知節點平均跳距的改進，同時利用平均跳距作用域減小計算未知節點與錨節點之間距離時產生的誤差。仿真結果表明，本文所提改進算法在一定程度上提高了節點的定位精度。

1 傳統DV-Hop定位算法[9]誤差分析

1)平均跳距誤差：錨節點通過無線傳感器網絡中的其他錨節點坐標和相互之間的跳數得到平均跳距，未知節點直接選取距離最近的錨節點的平均跳距作為本身的平均跳距；在這個過程中，傳統DV-Hop算法并未對錨節點平均跳距計算以及未知節點平均跳距選取過程產生的誤差作處理，直接參與最小二乘法的計算會造成誤差累積。

2)距離計算誤差：DV-Hop算法通過未知節點的平均跳距與最小跳數的乘積來估計未知節點和錨節點間的直線距離，在這個過程中誤差的產生有2方面：利用折線距離代替直線距離所產生的不可消除誤差；在計算折線距離時忽略每個跳段距離的差異，統一用未知節點的平均跳距代替所產生的誤差。后者可以通過本文提出的平均跳距作用域減小或消除。

2 DV-Hop定位算法的改進

2.1 錨節點平均跳距的改進[10]

本文改進策略包括首先剔除會引入較大誤差的錨節點，其次將參與計算的錨節點進行加權處理。

對于矩形分布區域來說，定義最大理想跳數k為

(1)

式中d1～d4為錨節點i距離矩形分布范圍4個頂點的距離。在理想情況下平均跳距與通信半徑接近，當錨節點接收到距離其他錨節點的最小跳數超出了節點分布范圍的最大理想跳數說明該路徑中錨節點間的共線度較低，將其剔除。

采用加權處理的方法計算錨節點i的平均跳距。定義

(2)

式中dij為錨節點i和j之間的實際距離；R為通信半徑；hopsij為錨節點i和j之間的最小跳數。錨節點j在參與錨節點i平均跳距計算過程中，其權重為

(3)

式中m為參與錨節點i平均跳距計算的錨節點個數。錨節點i的平均跳距為

(4)

2.2 未知節點平均跳距的改進

本文基于文獻[3，11]對未知節點平均跳距進行了改進，當錨節點和未知節點在一跳范圍內時，未知節點直接取最近的錨節點的平均跳距作為自己的平均跳距；未知節點和錨節點間最小跳數在1～M跳之間時取M跳內的所有錨節點平均跳距的均值；未知節點和錨節點之間最小跳數在M跳之外，取全局平均跳距。即未知節點k的平均跳距為

(5)

式中m為未知節點k周圍M跳范圍內的錨節點個數；n為整個無線傳感器網絡中的錨節點個數。閾值M為

式中A為整個無線傳感器網絡覆蓋區域面積；Lh為每個未知節點定位需要的平均錨節點個數；Tn為節點總數；Lp為錨節點比例；Hmax為錨節點和未知節點之間最小跳數的最大值。在滿足網絡中所有未知節點定位的情況下，M選取最小值參與運算；在節點分布不均的場合，閾值M需要選擇略大一些，以滿足整個網絡的覆蓋[11]。

按照式(5)，未知節點在不同情況下，根據與錨節點之間的最小跳數選擇不同的平均跳距，克服了傳統DV-Hop算法中單純采用最近的錨節點的平均跳距帶來的誤差，同時，當未知節點和錨節點在1跳范圍內時又保證了平均跳距的精度。

2.3 平均跳距作用域改進

當錨節點和未知節點附近的節點密度差別較大時，二者的平均跳距差別較大，單純采用未知節點的平均跳距計算距離會造成較大誤差。本文提出了平均跳距作用域，根據前述得到錨節點平均跳距和未知節點平均跳距，在計算未知節點到錨節點的距離時靠近未知節點的一半跳數采用未知節點平均跳距計算距離，另一半采用錨節點平均跳距。計算過程如下

dik=Hopsizei×hopsit+Hopsizek×hopstk

(6)

式中Hopsizei為錨節點i的平均跳距；Hopsizek為未知節點k的平均跳距，且滿足

hopsit=hopstk=hopsik/2

改進后的DV-Hop定位算法具體步驟如下：

1)錨節點通過未知節點的轉發得到其他錨節點的坐標及與其他錨節點間的最小跳數；

2)按照2.1節的篩選原則選取參與平均跳距計算的錨節點并進行加權處理得到錨節點平均跳距；

3)按照2.2節的選取原則決定每個未知節點的平均跳距；

4)根據平均跳距作用域計算未知節點到錨節點的距離；

5)未知節點利用最小二乘法完成定位。

3 仿真分析

為了驗證本文算法的有效性，在MATLAB平臺仿真分析，同時與文獻[3，11]中的改進策略進行對比。仿真模型為100個節點隨機分布于100 m×100 m的區域內，考慮不同錨節點比例、節點通信半徑對定位誤差的影響。未知節點k的定位誤差為

(7)

每個實驗重復進行100次，取平均值作為最終結果，在通信半徑R=30 m時比較錨節點比例對定位誤差的影響，結果如圖1所示。隨著錨節點比例的增大，4種算法的定位誤差均減小；錨節點比例較小時，無線傳感器網絡區域中錨節點分布不均勻，隨機性大，文獻[3，11]改進方案中大部分未知節點選取全局平均跳距作為自身跳距，而本文算法通過1跳和閾值M的雙重分割具有明顯效果。當錨節點比例在15 %～30 %時，文獻[11]中利用閾值M的定位效果優于文獻[3]中單純1跳分割的方案，而本文算法在閾值基礎上再次分開處理，效果更好。錨節點比例超過30 %時，定位誤差隨著錨節點增大不再明顯減小，本文算法仍優于其他算法。

圖1 不同錨節點比例下的定位誤差

在錨節點比例為20 %時，比較通信半徑對定位誤差的影響，結果如圖2所示。隨著通信半徑的增大，各種算法的定位誤差均減小；當通信半徑小于25 m時，1跳距離小，文獻[3]相比本文改進算法和文獻[11]有更多的未知節點選取全局平均跳距作為自身平均跳距帶來了誤差的累積，當通信半徑大于28m時，錨節點經過篩選與加權后得到平均跳距取得了較好的效果，同時，平均跳距作用域進一步減小了誤差，本文算法相比其他改進算法均有不同程度的優勢。

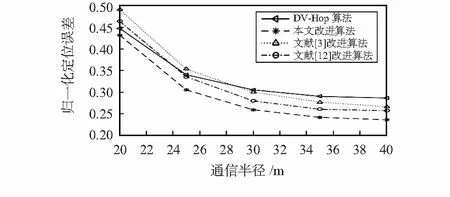
圖2 不同通信半徑下的定位誤差

4 結束語

針對無線傳感器網絡中節點自定位誤差較大的問題，對傳統DV-Hop定位算法進行了改進，仿真結果表明：在錨節點比例適中、通信半徑較小的情況下本文算法可以減小定位誤差，提高定位精度，適用于低功耗、大范圍的無線傳感器網絡環境。

[1] Niculescu D,Nath B.Ad hoc positioning system (APS) using AOA[C]∥The Twenty-Second Annual Joint Conference of the IEEE Computer and Communications,IEEE Societies,INFOCOM 2003,LEEE,2003:1734-1743.

[2] 向滿天,王 勝,楊友華.基于閾值機制與距離校正的 WSN s改進 DV-Hop 定位算法[J].傳感技術學報,2016,29(6):920-926.

[3] Shi Q,Zhou J,Zhang J,et al.An improved scheme for DV-Hop in WSNs[C]∥11th International Conference on Wireless Communications,Networking and Mobile Computing,WiCOM 2015,IET,2015:1-4.

[4] 宋倩雯,郭松濤,柏艾林,等.無線傳感器網絡中一種改進的DV-Hop定位算法[J].重慶大學學報,2015,38(4):128-136.

[5] Shen S,Yang B,Qian K,et al.An efficient localization algorithm in wireless sensor networks[C]∥International Symposium on Computing & Networking,IEEE,2015:291-294.

[6] 趙芝璞,吳 棟,王 艷,等.基于平均跳距和位置優化的改進 DV-Hop 定位算法[J].系統仿真學報,2016,28(6):1273-1280.

[7] 白 偉,李鳳英,鄭海洋,等.基于BADV-Hop的無線傳感器網絡節點定位方法[J].傳感器與微系統,2014,33(10):118-120.

[8] 何登平,范茂林.一種基于APIT的無線傳感器網絡混合型定位算法[J].傳感器與微系統,2015,34(2):133-135.

[9] Kumar S,Lobiyal D K.An advanced DV-Hop localization algorithm for wireless sensor networks [J].Wireless Personal Communications,2013,71 (2):1365-1385.

[10] Wang Y,Qian K.An improved DV-Hop positioning algorithm based on Hop distance correction[C]∥2014 11th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP),IEEE,2014:415-418.

[11] Hu Y,Li X.An improvement of DV-Hop localization algorithm for wireless sensor networks[J].Telecommunication Systems,2013,53(1):13-18.