土方量計算中的方格網法邊長最優選擇分析
萬義有 李勇華 王小衛

摘 要:土方量計算的基本方法有許多種,在實際工程應用中,同一施工場地采用不同的方法,計算結果往往不同,有時差別很大,因此不同計算方法的合理選擇就顯得十分重要。方格網法計算土方量,方格網邊長的選擇受人的主觀影響因素很大,因此,如何選取最優邊長,節省施工成本,非常具有研究價值。本文就方格網法計算土方量,不同方格網邊長的合理選擇做了理論分析,并通過程序實現了土方量的相對誤差的計算,為實際生產提供理論依據。
關鍵詞:土方量計算 方格網法 邊長最優
中圖分類號:P258 文獻標識碼:A 文章編號:1672-3791(2018)07(a)-0065-04
在土方計算的方法中,當涉及求取土方量填挖平衡時,使用最多的一種方法就是方格網法,對于平坦場地,在設計要求填挖方量基本相等,即土方就地平衡,由于土方量工程量比較大,動輒幾萬方、幾十萬方,甚至更多,如果計算誤差量較大,對工程費用成本影響就很大,因此對造成偏差的諸多因素進行合理的分析很有現實意義。而方格網法計算土方量,方格網邊長的選擇受人的主觀影響因素很大,因此,如何選取最優邊長,節省施工成本,非常具有研究價值。
1 方格網法計算原理與公式
方格網法計算土方量的基本原理是:在施工區域內繪制好方格,以設計標高所在平面作為土方量立體模型計算的底面,利用地形圖上采集到的高程點,通過選取合理的曲面擬合算法,用采用雙線性內插的方法,內插出方格網角點上的標高,再分別計算各個格網的填挖方量,然后分別累加全部方格網的土方量即得最終填方量和挖方量。
在使用方格網法計算場地土方量時,主要的工作是劃分格網、確定設計標高、計算方格網角點的施工高度、內插“零點”位置、繪制零線、計算每個方格土方量、計算土方總量。
1.1 劃方格網
選取測區所在地的大比例尺(最好是1∶500~1∶2000)的地形圖,以此作為設計底圖,根據底圖設計劃分方格 網。在劃分方格網時,要盡量考慮測區的地形走勢和施工 坐標系的坐標軸的方向一致,把測區劃分成多個完整的方 格,方格網邊長一般取值為:10~40m[2]。對于不同的工程,如不同的場平面積、施工高度、地形坡度、地形圖比例尺、等高距等[1],通過有效的計算方法,求取方格網邊長最佳值,使計算的土方量偏差量盡可能小,降低工程成本。
1.2 確定設計標高
(1)在施工場地上建立方格網,如圖1所示。圖中方格網角點標示的是角點的地面標高。
這便是一般常用的計算公式[3]。
式中:H0為設計標高;H1、H2、H3、H4為各角點、邊點、凹點、中間點的自然地面的標高;N為方格數;a為每個方格 的邊長。
1.3 計算角點施工高度
方格網角點施工高度等于設計地面標高和自然地面標高之差,公式如下。
1.4 計算零點位置并確定零線
零線是填方與挖方的交界線,即填挖平衡線,在零線上,既無挖方量也無填方量。如果在一個方格網內同時存在填方和挖方時,首先按照方格網零點計算公式,求取計算出零點在方格上的位置,并標注在地形圖上的方格網邊線上,連接所有零點,即可繪制出填挖平衡線,即是零線。
1.5 計算方格土方量
方格網法計算土方量,是將土體看作成若干個四棱柱體或是三棱柱體組成,通過計算柱體的體積,來計算土方量。在算法上,它們都是通過把填挖方的土體劃分成多個多面體來計算體積。這樣的簡化方法不僅降低了土方量的計算誤差,而且還為計算機程序代碼的編寫提供了可能,大大提高了計算效率,對實現土方量計算自動化具有重要意義。
2 方格網法精度分析
2.1 土方量精度模型
可以將地形表面看作由無限個底面邊長為a的四棱柱組成,由于地形表面是非規則曲面,每個柱體表面可以近似看作是雙線性曲面,正方形格網的下表面均為水平面(平均設計標高所在的平面),如圖2所示,土方量由四棱柱體積進行累加得到。正方形格網的體積為:
σa為點A和點B之間所有點的平均方差。
N為小方格總數。
M為地形圖比例尺的分母。
σ0為等高線高程標準差(m)。
σL為量取方格網邊長時的標準差(m)[4]。
以上涉及的各量均采用國際標準單位,土方量相對誤差值為百分比。
以上土方量相對誤差計算公式,可以由VB開發,程序運行界面如圖3所示。
2.2 土方量相對誤差表與曲線圖
根據式(6),結合開發的程序代碼,對于以上6個參數(方格網邊長a、場平面積S、施工高度平均值H、地形圖等高距d、地形圖比例尺M、平均地形坡度α),分別可以計算生成土方量相對誤差計算表。計算結果如表1所示。
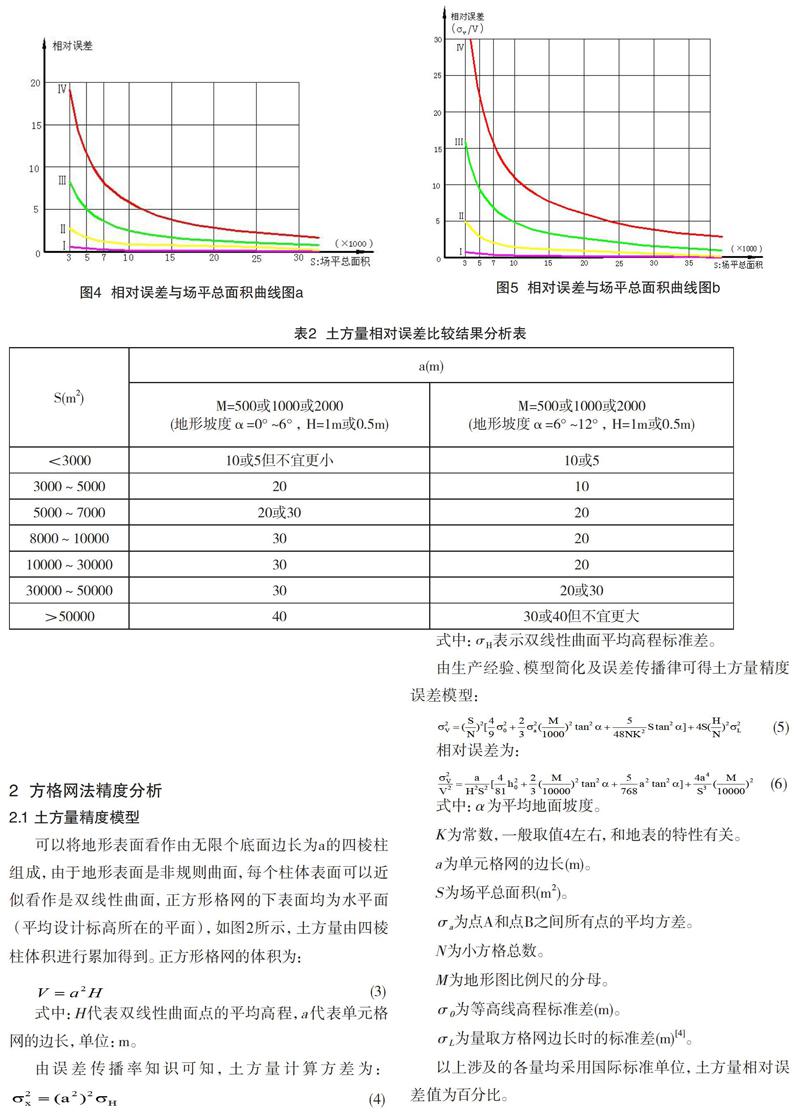
根據上述公式,采用編寫的計算機程序代碼,設置好 計算參數,自動生成計算表,根據表格自動繪制相對誤差 與場平總面積曲線圖(見圖4、圖5)。
比例尺為:1∶500,平均地形坡度為:6°;S為場平總面積(m2),為土方量相對誤差。
圖中的Ⅰ、Ⅱ、Ⅲ、Ⅳ表示方格網邊長取值分別為:10m、20m、30m、40m。
由上面的土方量相對誤差列表1可以得出:
(1)比例尺為1∶500,其他的1∶500、1∶1000、1∶2000曲線圖類比圖4、圖5,這里不再贅述。
(2)比例尺為1∶500,地形坡度為12°,等高距為1m時的相對誤差曲線圖。
3 結語
對于不同地區、不同面積范圍的方格網邊長取值是一個很重要的問題,它關系到最后計算精度的問題,能取到最優的方格網邊長對計算結果很重要。從上面的曲線圖可以看出,當影響土方量相對誤差的6個因素(方格網邊長a、場平面積S、施工高度平均值H、地形圖等高距d、地形圖比例尺M、平均地形坡度α)中,后5個因素確定時,即取值確定,方格網邊長和土方量相對中誤差成正相關,但是方格網邊長取值變小時,使得格網劃分得更細,這樣就大大增加了計算的數據量和復雜程度,明顯地增加了土方量計算的難度,因此可根據具體工程項目的具體要求,在綜合考慮成本和計算難度的基礎上,按照上述模型用計算機程序去求得最合適的方格網邊長。
根據上述模型公式,結合計算程序代碼,計算出在不同影響因素條件下,可以得出表2的結論,用于指導實際生產中方格網法計算土方量邊長的最合理選擇。從相對精度和工程量成本考慮,一般應在大于1∶2000比例尺圖上進行設計計算,而且要求土方量計算的相對誤差小于5%,方格網的邊長選取最好不超過40m。
表2的分析結果可以作為方格網邊長最優選擇的參考依據;現在由于計算機性能的不斷提高,處理數據的速度不斷增快,可以在實際理論分析的基礎上適當地縮短方格網的邊長,使計算結果更精確,提高計算精度,使計算結果與實際土方量更吻合。當實際情況與假設不同時,可根據附錄中的土方量相對誤差計算程序計算,求出相應的相對誤差值,并繪制出相對誤差曲線圖,以結合實際情況合理確定最優的方格網邊長。
參考文獻
[1] 張海印.土方計算精度與方格網邊長之關系的研究[J].華東地質學院學報,2000,23(1):70-73.
[2] 李斯.測繪技術應用與規范管理實用手冊[M].北京:金版電子出版公司,2002.
[3] 姜衛杰.不規則場地設計標高的計算及應用[J].山東建筑工程學院學報,1997,12(1):80-83.
[4] 蔣功旺.工程土方量DEM與方格網計算精度分析[J].建材與裝飾,2008(4):408-409.

