冰載荷下冰速與冰厚對平臺動力響應的影響①

梁 瑞 孟祥鼎

(蘭州理工大學石油化工學院)

從20世紀中葉海洋平臺興起時，冰載荷對平臺的影響已經逐漸被人們重視。目前，已有多座平臺受冰激振動的影響而下陷、倒塌，渤海JZ20平臺受冰激振動影響緊急停產，造成了巨大的損失。為了研究冰激振動對平臺的影響，諸多學者基于不同的力學方法，得出了強迫振動理論、冰與結構相互作用理論和自激振動理論這3種理論。在所有的冰激振動理論中，冰速、冰厚均是極為重要的環境參數。筆者基于ANSYS軟件，通過對不同冰速、冰厚下平臺動力響應的模擬分析，研究了冰速和冰厚在冰激振動中的作用，對平臺的安全設計生產具有一定的參考價值。

1 冰激振動理論研究

1.1 強迫振動理論

系統在外界的持續激勵下產生的振動稱為強迫振動。Peyton H R等觀測到海冰擠壓結構的過程中，海冰的破碎頻率始終保持在一定范圍內，據此認為海冰的破碎頻率只與海冰本身的固有性質有關[1,2]。Loset S等提出擠壓冰力是一個關于結構尺寸、冰抗壓強度、冰厚和冰速的函數[3,4]。強迫振動理論的動力平衡方程可以表示為：

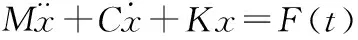
(1)

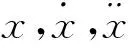
1.2 冰與結構相互作用理論

強迫振動理論雖能解釋冰力具有周期性并且其函數圖像呈鋸齒狀這一現象，但無法解釋在一定條件下冰的破碎頻率和結構的自振頻率相同，結構發生共振且振幅明顯，帶有巨大的破壞性。Sodhi D S發現在一定冰速范圍內，冰速越大，擠壓冰力越大[5～9]。劉健等通過考慮冰抗壓強度與應力速率之間的關系，對Matlock模型進行了適當的修改，使之同時適用于剛性結構和柔性結構[10]。彭星來等采用ALGOR軟件對平臺進行冰激振動分析，驗證了冰與結構相互作用理論[11]。

由此冰與結構相互作用理論被提出，這一理論在支持冰力的周期性的同時，還提出冰排在擠壓結構的過程中，不僅僅有冰排對結構的作用力，結構也在對冰進行著反作用，最終兩者趨向一致，即產生耦合現象。在冰與結構相互作用理論中，動力平衡方程可以表示為：

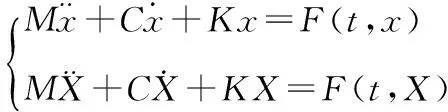
(2)

1.3 自激振動理論

自振系統由恒定的能源、振動系統和調節器3部分構成，系統依靠外界的能量作為補充，以自身為調節器，控制能量的輸入。強迫振動理論和冰與結構相互作用理論雖然在結構是否對冰有反作用這一方面具有分歧，但都認同冰力具有周期性。自激振動理論認為冰力不具有周期性，但是因為海冰的強度是一個隨加載速率變化的函數，當加載速度在一定范圍內變化時會產生負阻尼，使得冰力呈現出周期性變化規律。

自激振動理論冰速與結構響應速度的函數可以表示為[12]：

(3)

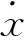
(4)

根據式(3)、(4)可以得出冰阻尼系數φ和應力σ之間的函數關系：

(5)

由此可以看出，自激振動的觸發條件十分苛刻，只有φ為負數時才會產生負阻尼，從而引發自激振動現象。自激振動的條件函數可以表示為[13]：

(6)

式中，ξi、ωi、Mi*、uki分別為第i階振型的阻尼比、圓頻率、廣義質量和自由度k的振型值，φkk為冰阻尼系數，m為振型總數。

2 平臺模型

2.1 平臺工況

本文研究的是六腿導管架式海洋平臺，平臺主要可以分為3部分，分別是樁基、導管架和上部組件，其中樁基和導管架統稱為支撐結構，主要用來支撐甲板和位于甲板上的設備。導管架頂部標高80m，泥面標高0m，從泥面至導管架頂部每隔一定距離均采用φ508mm×16mm規格桿件設置水平拉筋將6個樁腿依次相連，并在樁腿間設置X形剪刀撐，共計4層，每層共有10個桿件，層與層之間有斜撐，兩個方向斜度均為1∶10。上部組件主要是由上下甲板以及甲板建筑組成。平臺頂部標高98m，甲板上鋪滿8mm厚鋼板，梁與立柱之間用鋼管焊接，并采用φ608mm×18mm規格桿件架立斜撐。

2.2 模態分析

平臺模型采用ANSYS進行建模，將水面連接桿件和導管架之間連接的交點設立為節點，將導管架質量集中到節點上，節點模擬為理想化剛性節點，可用來傳遞彎矩、剪應力和軸應力。為了便于計算，簡化了甲板模型，甲板橫梁采用beam188單元進行模擬，甲板平面采用shell63單元，采用mass21質量單元模擬甲板及上部設備的質量[14]。導管架水下部分采用pipe59單元進行模擬，水上部分采用pipe16單元進行模擬。平臺樁基采用等效樁的形勢，樁腿直徑1.2m，取泥面下導管架平臺6倍樁徑處為剛性固定端。建立的平臺模型如圖1所示。對平臺進行模態分析，得到的結果見表1。

圖1 平臺模型

振型階數頻率/Hz11.259821.317432.110443.263853.5530

2.3 動冰力函數

一般而言，海冰的破壞形式可以分為3種，即擠壓破壞、彎曲破壞和屈區破壞。對于柔性直立體結構，擠壓冰力對結構的影響最大，通常將作用在柔性直立體結構上的擠壓冰力稱為海冰的靜冰力。對于海冰靜冰力的計算，可以分為兩類，即半經驗半理論公式和完全經驗公式。半經驗半理論公式可以寫為以下通式[15]：

F=αDHσc

(7)

其中，F為海冰靜冰力；α代表修正系數(例如接觸系數k、局部擠壓系數I及性質系數m等)；D為樁柱直徑；H為冰厚；σc為冰單軸抗壓強度。

這類公式有一個典型的特征是量綱相同，因為它們是基于理論推導得到的公式，區別在于各自有自身的修正系數。半經驗半理論公式中比較有代表性的是Korzhavin-Afanasev公式，也是應用最廣泛的公式，表達式可以為：

F=ImkDhσc

(8)

其中，I為局部擠壓系數；m為考慮結構與冰接觸面形狀的系數；k為接觸條件系數。

完全經驗公式可寫為以下通式：

F=βD0.5Hγσc

(9)

其中，β和γ為修正系數。此類公式是基于現場觀測到的數據擬合而成，通用性差，當環境條件發生變化時會產生較大誤差。

當結構發生穩態振動時，冰力頻率被鎖定在結構的固有頻率上，此時結構的振幅達到峰值[16]。穩態振動下擠壓冰力函數可表示為[17]：

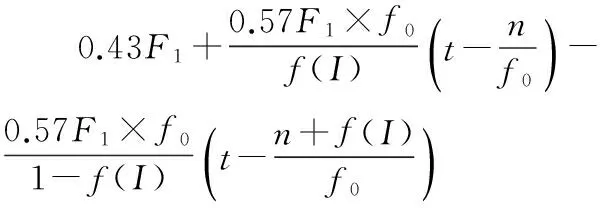
(10)

其中，f0為系統自振頻率；F1為最大靜冰力；f(I)為相互作用系數。

2.4 平臺工況下動力響應

在模擬工況下平臺動力響應時，需要計算出平臺的環境載荷、平臺阻尼和冰力折減系數[18～20]。根據實測的環境數據，冰厚取50年重現期的冰厚0.4m，冰速取遼東灣多點測量的平均冰速0.43m/s，冰單軸抗壓強度取2.3MPa，海風力為21 732.48N，海流力為3 764.75N。平臺阻尼可以根據阻尼矩陣的定義式和瑞雷阻尼公式聯立求得。冰力折減系數計算公式為[21]：

Fs=f(s,θ)RnFi

(11)

其中，Fs為作用于多腿結構上的總冰力；Rn為折減系數，與各樁柱前冰的非同時破壞有關，保守計算取1.0。Fi為單樁柱的冰力；f(s,θ)為放大系數，是多腿結構上的總冰力對單樁冰力的比值，與樁柱的布置、迎冰角等有關，實際上是各樁的子相互作用系數之和，根據本文所采用導管架平臺模型，f(s,θ)取4.74。

工況下平臺的動力響應如圖2所示。

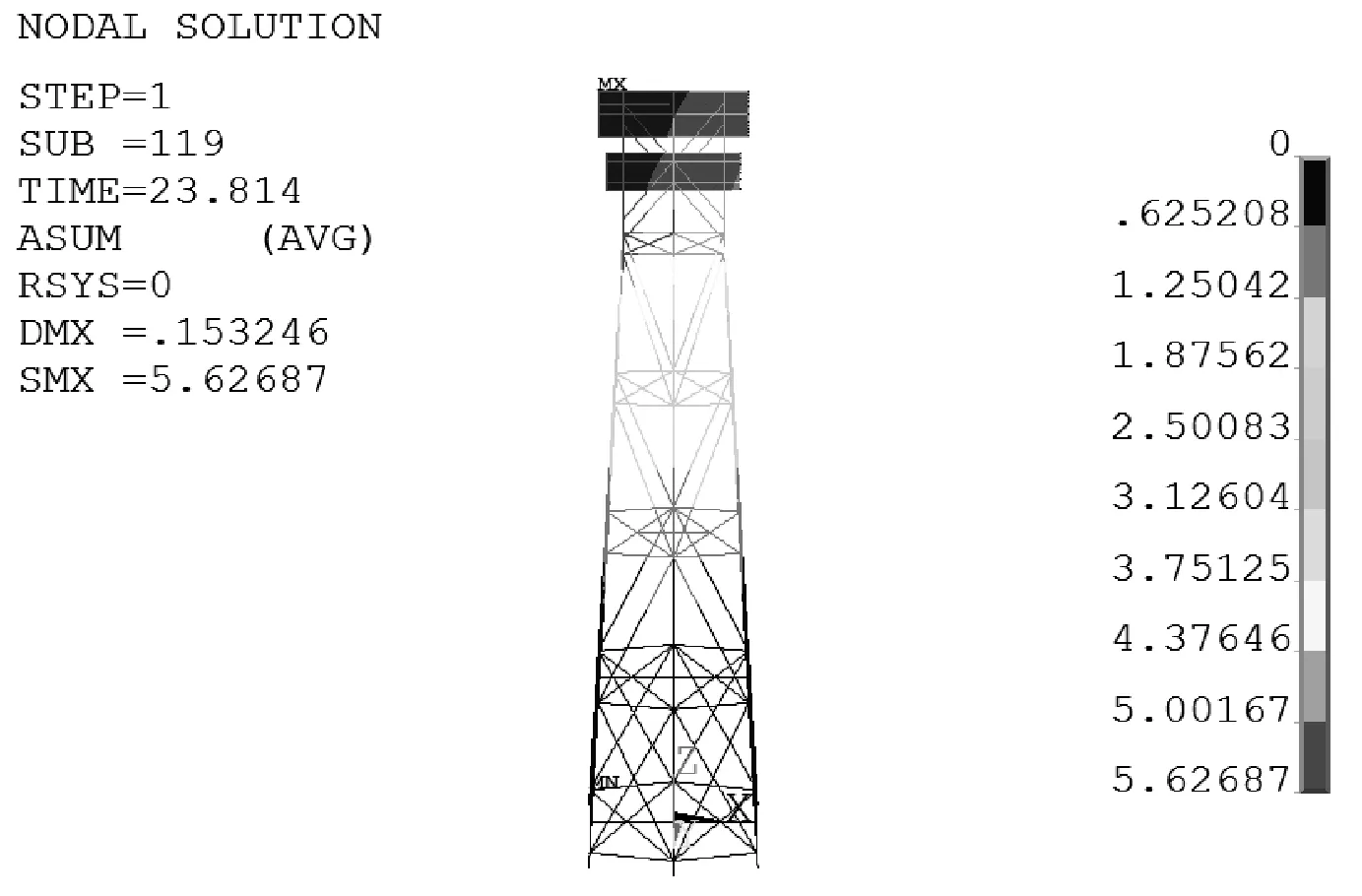
圖2 工況下平臺的動力響應

3 不同冰速、冰厚下平臺的動力響應

3.1 冰速對平臺的影響

當冰與結構發生共振時，冰力對平臺的影響最大，冰速過大或者過小時，均不易與結構發生共振[22～24]。因此在模擬分析中，選用冰速0.2～0.8m/s這一區間，其余參數同工況。因數據較多，筆者只列舉冰速0.2、0.3、0.4、0.5、0.6、0.7、0.8m/s情況下平臺的最大位移響應、速度響應和加速度響應見表2。

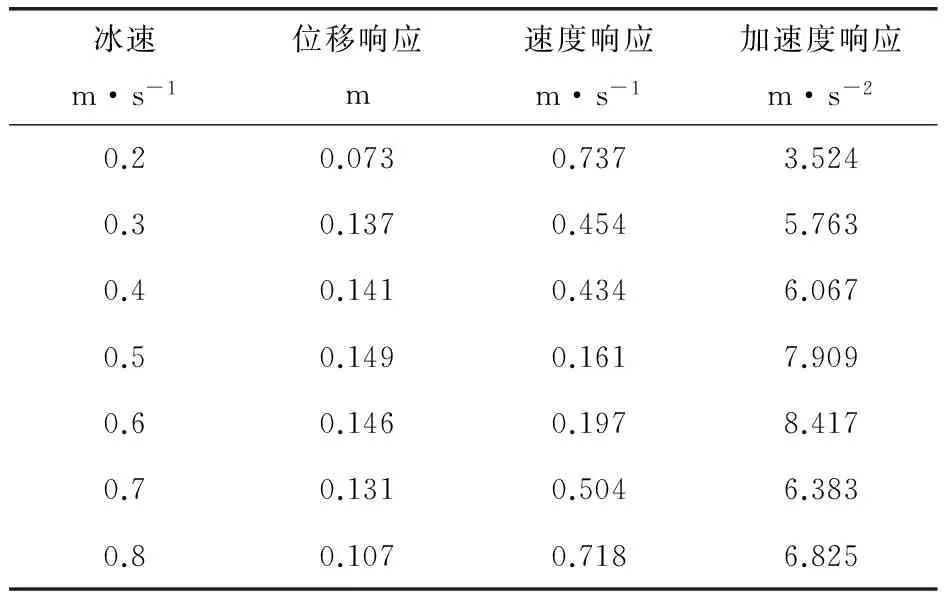
表2 不同冰速下平臺的動力響應

根據得到的數據可以看出，隨著冰速的增加，平臺的位移和加速度呈現先增加后減小的趨勢，平臺的速度呈現先減小后增加的趨勢。當冰速達到0.5～0.6之區間時，平臺的位移和加速度到達最大值，速度達到最小值。這是因為冰速在這個區間內時，冰與結構的共振最為強烈，此時平臺的位移和加速度到達最大值，而平臺的劇烈振動是因為平臺加速度發生劇烈變化引起的，所以此時作用在加速度上的時間周期明顯縮小，平臺的速度反而達到最小值。因此冰速越接近這個區間，平臺位移和加速度越大，速度越小。

取冰速0.5m/s時節點171的加速度時程圖表征平臺的加速度，該節點是上部甲板平臺邊緣點，也是平臺加速度變化最為劇烈的地方，如圖3所示。

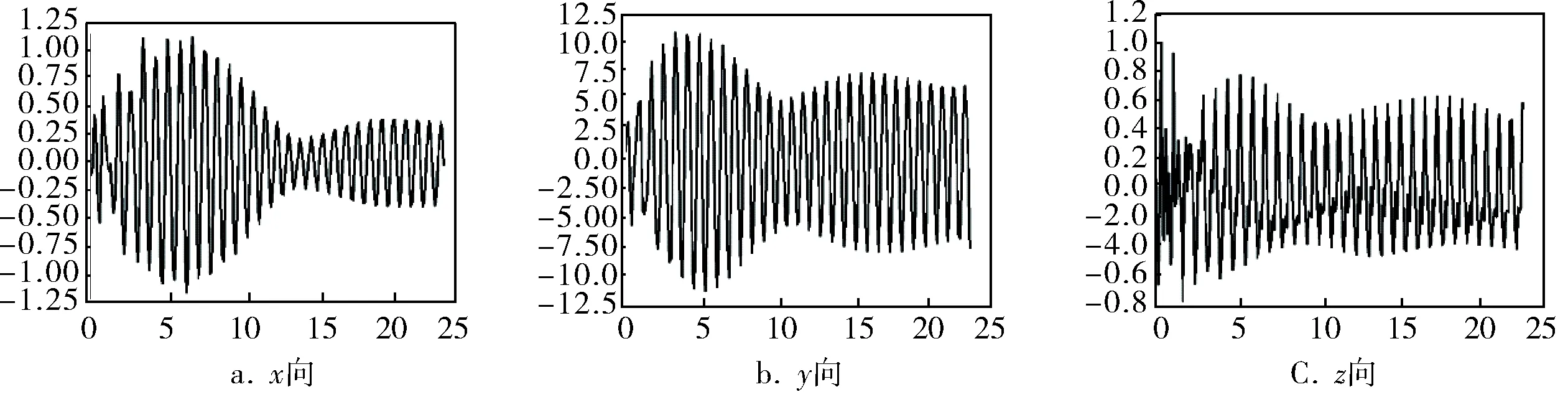
圖3 節點171加速度時程圖

3.2 冰厚對平臺的影響

在模擬分析中，選用冰厚0.2、0.3、0.4、0.5、0.6、0.7、0.8m這一區間，各冰厚下平臺的最大位移響應、速度響應和加速度響應見表3。

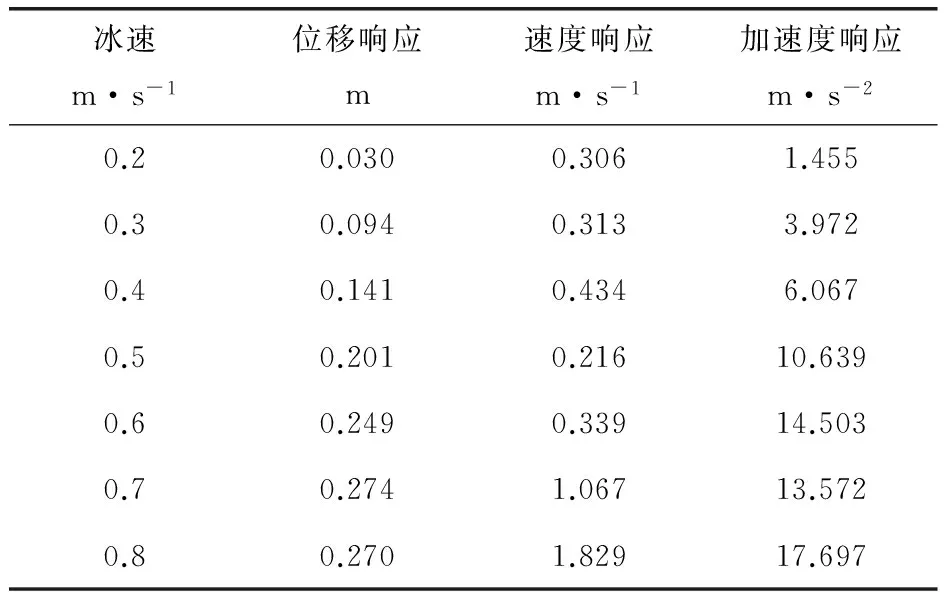
表3 不同冰厚下平臺的動力響應

從得到的數據可以看出，隨著冰厚的增加，平臺加速度和位移響應會持續性增加，平臺的速度出現先增加，后減小，再增加的變化形勢，這是因為隨著平臺加速度響應的不斷增加，平臺對海冰產生的反饋不同，海冰的破壞形式發生了變化。

4 結論

4.1平臺甲板邊緣點和平臺桿件交匯的節點是平臺的危險點，在這些位置需要考慮平臺的疲勞效應和裂紋擴展，應對這些位置制定計劃進行定期檢測和維護工作。

4.2冰速的改變對靜冰力大小的影響較小，更多的是影響冰與結構相互作用系數，從而使平臺的動力響應產生變化。當冰速在一定范圍內時，冰與結構發生穩態振動，此時海冰對平臺產生的破壞最大。冰速越遠離這個范圍，海冰對平臺動力響應的影響越小。

4.3冰厚的改變不僅僅影響冰與結構相互作用系數，還會使靜冰力發生大幅度變化。當冰厚不斷增加時，平臺的位移響應也在不斷增加，海冰對平臺的破壞性也逐漸增大。

4.4不同的冰速和冰厚會改變平臺對冰排的反饋作用，一定程度上支持了自激振動理論。

[1] Peyton H R. Sea Ice Forces[C]. Ice Pressures Against Structures. Ottawa: National Research Council of Canada, 1968: 117～123.

[2] Neill C R. Dynamic Ice Forces on Piers and Piles：an Assessment of Design Guidelines in the Light of Recent Research[J]. Canadian Journal of Civil Engineering, 1976, 3(2): 305～341.

[3] Loset S, Shkhinek K. Evaluation of Existing Ice Force Prediction Methods[J]. LOLEIF Rept, 1999, 3(8)：248～256.

[4] Loset S, Shkhinek K N, Uvarova E. An Overview of the Influence of Structure Width and Ice Thickness on the Global Ice Load[C]. POAC’99.Ottawa:Proceedings of the Port and Ocean Engineering Under Arctic Conditions, 1999: 425～434.

[5] Sodhi D S. Crushing Failure During Ice-Structure Interaction[J]. Engineering Fracture Mechanics, 2001, 68(17)：1889～1921.

[6] Sodhi D S. Nonsimultaneous Crushing During Edge Indentation of Freshwater Ice Sheets[J]. Cold Regions Science and Technology, 1998, 27(3): 179～195.

[7] Sodhi D S, Takeuchi T, Nakazawa N, et al. Medium-scale Indentation Tests on Sea Ice at Various Speeds[J]. Cold Regions Science and Technology, 1998, 28(3)：161～182.

[8] Takeuchi T, Akagawa S, Saeki H, et al. Ice load Equation for Level Ice Sheet[J]. International Journal of Offshore and Polar Engineering, 2002, 12(3):171～177.

[9] Shkhinek K, K?rn? T, Kapustiansky S, et al. Influence of Ice Speed and Thickness on Ice Pressure and Load[C]. POAC’01. Ottawa:Proceedings of the International Conference on Port and Ocean Engineering Under Arctic Conditions. 2001.

[10] 劉健,陳國明,楊曉剛，等. 基于ANSYS軟件實現平臺結構的冰激振動分析[J]. 中國海上油氣,2005,17(1):65～69.

[11] 彭星來,徐華福,蔡宗虎，等. 基于ALGOR軟件對導管架平臺結構冰激振動響應分析[J]. 中國海洋平臺,2010,25(5):33～37.

[12] 黃焱. 冰激海洋平臺振動的動力模型試驗研究[D].天津:天津大學,2004.

[13] 陳德彬,徐繼祖. 海冰作用下導管架平臺的動力分析[J]. 海洋工程,1988,(1):32～40.

[14] 韓春杰,井丹丹,張海莉. 基于ANSYS的水平井鉆柱橫向振動分析[J]. 化工自動化及儀表, 2016, 43(4): 389～391,407.

[15] 史慶增. 孤立樁柱上冰壓力的經驗公式 計算法及試驗驗證[J]. 海洋工程,1993,(1):1～11.

[16] 韓春杰,張海莉,井丹丹. 基于ANSYS的鉆柱縱向振動諧響應規律研究[J].化工自動化及儀表,2015, 42(8): 904～907.

[17] 王譯鶴. 冰激窄體結構振動的機理與理論模型研究[D]. 大連:大連理工大學,2014.

[18] 俞樹榮,王在剛,劉雪,等. 波流作用下海洋立管流固耦合動力特性分析[J]. 化工機械,2013,40(5):653～657.

[19] 俞樹榮,馬龍,丁敏. 海洋平臺立管導波檢測的數值仿真和實驗研究[J]. 化工自動化及儀表,2013,40(8): 1040～1043.

[20] 陳團海,陳國明. 冰區平臺疲勞可靠性與參數敏感性分析[J]. 船海工程,2009,38(5):129～133.

[21] Kato K, Sodhi D S. Ice Action on Two Cylindrical Structures[J]. Journal of Energy Resources Technology, 1984, 106(1): 107～112.

[22] 黃焱,史慶增,宋安. 冰激柔性直立四樁柱結構振動的模型試驗[J]. 天津大學學報,2009,40(5):388～393.

[23] 齊念. 冰激橋墩振動模型試驗研究及冰荷載的識別[D].大連:大連理工大學,2009.

[24] 盧云亮. 基于離散元—有限元方法的導管架海洋平臺冰激振動分析[D].大連:大連理工大學,2015.