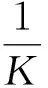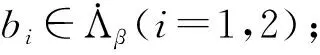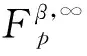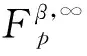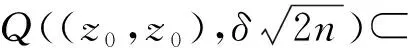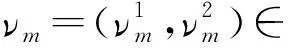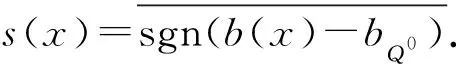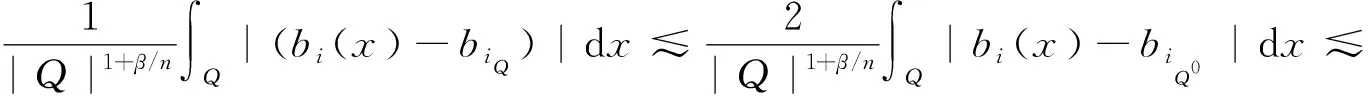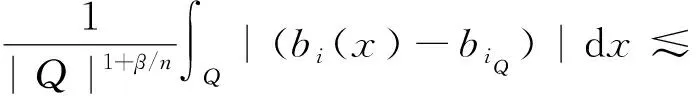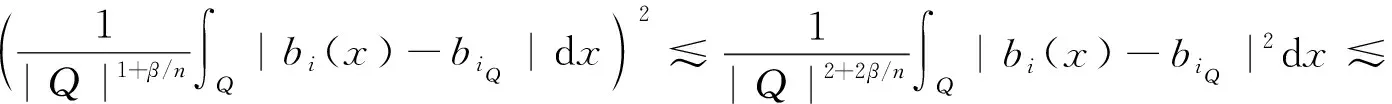雙線性Calderón-Zygmund算子交換子在Triebel-Lizorkin空間上有界的充分必要條件
房成龍
(中國人民大學數學學院,北京 100872)
1 預備知識
1975年,Coifman和Meyer[1]首次研究了雙線性奇異積分算子,發現Calderón-Zygmund奇異積分算子交換子的研究可以歸結為一類雙線性奇異積分算子研究.隨后許多學者開始關注交換子及雙線性算子有界性問題.[2-10]
1976年,Coifman,Rochberg和Weiss[2]獲得了一個著名結果:Calderón-Zygmund奇異積分算子與BMO函數生成交換子在Lebesgue空間上有界,其結果大力推動了交換子的研究.之后,Pérez和Trujillo-Gonzle[3-4]推廣了交換子概念,并獲得了向量值奇異積分算子交換子的加權估計.
設β>0,若函數f滿足
特別地,1995年,Paluszynski[5]證明了
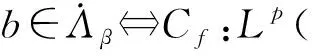
(1)
其中:Cf是Calderón-Zygmund奇異積分算子與Lipschitz函數生成交換子;0<β<1;1 2009年,王瑋和徐景實[7]獲得了雙線性奇異積分算子的Lipschitz交換子在乘積Lebesgue空間上的有界性. 2014年,默會霞和陸善鎮[11]證明了雙線性奇異積分算子與Lipschitz函數生成的迭代交換子從乘積Lebesgue空間到Lebesgue空間或Triebel-Lizorkin空間有界. 受這些研究啟發,自然產生一個疑問:能否用雙線性奇異積分算子有界性去刻畫Lipschitz空間?為了驗證這個疑問,本文首先討論了雙線性奇異積分算子的線性交換子(見定義1.1)從乘積Lebesgue空間到Lebesgue空間或Triebel-Lizorkin空間有界性,然后在對此疑問給出了肯定回答. K(x,y1,y2)是一個局部可積且遠離對角線x=y1=y2的函數,對參數A>0,ε>0,有: (2) (3) 其中|x-x′|≤1/2max{|x-y1|,|x-y2|}.滿足(2)與(3)式且與參數m,A和ε有關的K(x,y1,y2)稱為2-CZK(A,ε).特別地,若K(x,y1,y2)為K(x-y1,x-y2)形式時,所對應算子稱為卷積型算子. 定義1.1設K是2-CZK(A,ε),雙線性Calderón-Zygmund奇異積分算子T(f1,f2)定義為 若1 定義1.2設T是雙線性Calderón-Zygmund奇異積分算子,b是局部可積函數. (ⅰ)T的線性交換子[Σb,T]定義為 (ⅱ)T的迭代交換子[Πb,T]定義為 這部分主要討論[Σb,T]從Lebesgue空間到Lebesgue空間、Triebel-Lizorkin空間的有界性.文獻[8]中定理2獲得了雙線性奇異積分算子與Lipschitz函數生成的1階迭代交換子在Triebel-Lizorkin空間有界性,并能說明[Πb,T]在Triebel-Lizorkin空間有界性,故這里給出了定理2.2. 引理2.1設0<β<1,下面事實成立: (ⅰ)[9]若1 引理2.2設1 其中常數C與p,q,α和n有關. (2) [Σb,T]從Lp1(Rn)×Lp2(Rn)到Lr(Rn)有界. [Σb,T](f1,f2)=[Σ(b-bQ),T](f1,f2), 則 首先估計D1,運用引理2.1得 由于T是2-線性Calderón-Zygmund算子,則 結合下面不等式估計D8: 其中Q*?Q.這個不等式的證明可見文獻[9]. 由于 結合前面估計,可得 上面不等式兩面同時對所有包含x的方體Q取上確界后,再取Lp范數,運用引理2.1結論(ⅱ),即得 運用I1α從Lp1×Lp2到Lr有界性[10],即得 證明顯然 估計E1: 類似于定理2.1中D1與D2的估計,可估計E2: 同理可得 下面估計E7: 結合上面估計,運用引理2.1結論(ⅱ)即得 (3) [Σb,T]從Lp1(Rn)×Lp2(Rn)到Lr(Rn)有界; (3) [Πb,T]從Lp1(Rn)×Lp2(Rn)到Lr(Rn)有界. 證明根據定理2.1、定理2.2和文獻[8]中定理1,只需說明結論(2)—(5)中任意一個作為條件時,結論(1)成立. 令z1=δ-1z0,有 對所有滿足上面不等式的(y,z),可得 選擇x0∈Rn,t>0,令Q+Q(x0,t),Q0=Q(x0-z1t,t).固定x∈Q,y1,y2∈Q0,則有 根據上面事實即可得 (4) (3)?(1).類同上面的證明,由于1/r+1/r′=1,故 根據[Σb,T]從Lp1(Rn)×Lp2(Rn)到Lr(Rn)有界性,即可說明(3)?(1)成立. (4)?(1). 同理得(5)?(1)成立,結論證畢.
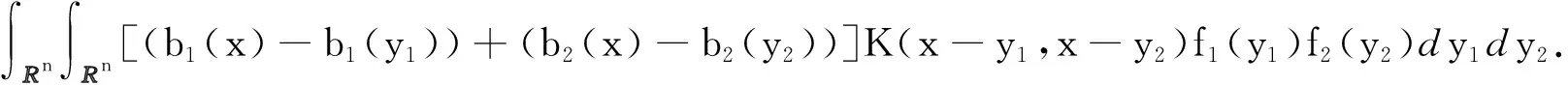

2 雙線性Calderón-Zygmund奇異積分算子的線性交換子在Triebel-Lizorkin空間的有界性
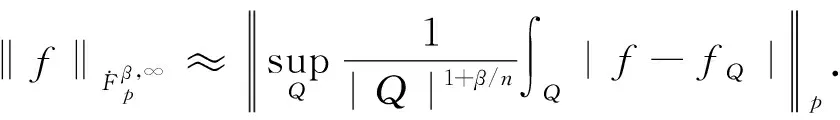
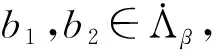
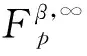
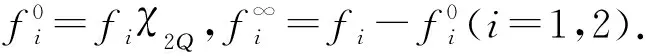
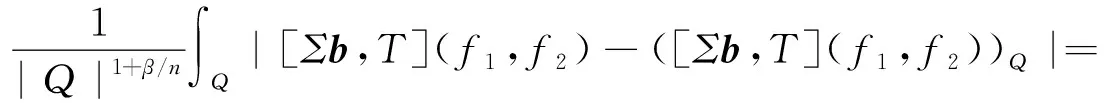
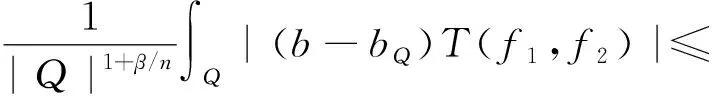
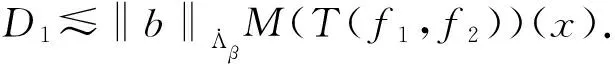

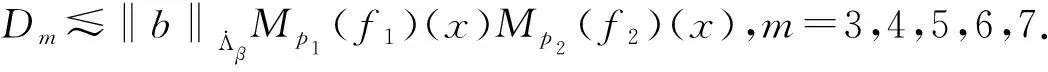
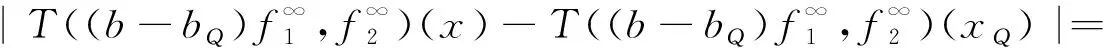
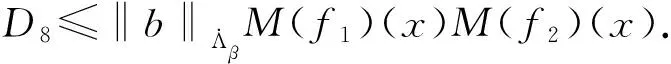
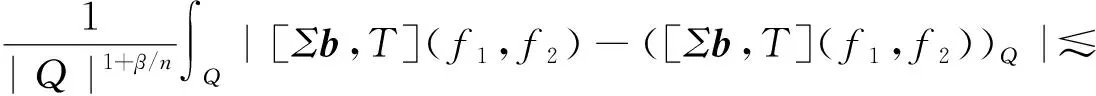
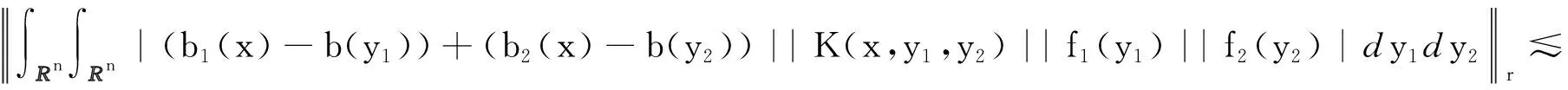
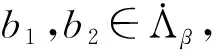
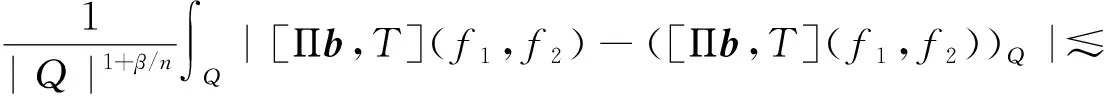
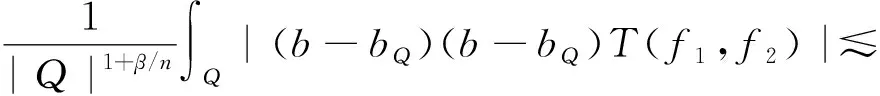
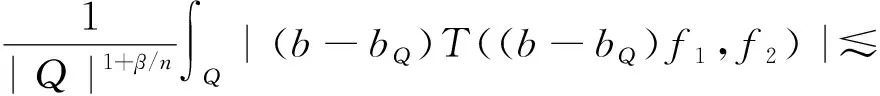
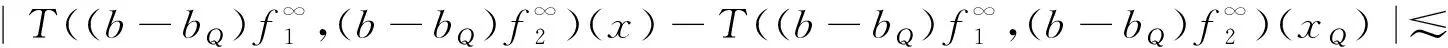
3 刻畫Lipschitz空間