水泵與水輪機轉子低壓截面上的結構常數G及流線相似法應用

張征驥，李 正，魏顯著，覃大清

?

水泵與水輪機轉子低壓截面上的結構常數G及流線相似法應用

張征驥，李 正，魏顯著，覃大清

（水力發電設備國家重點實驗室(哈爾濱大電機研究所)，哈爾濱 150040）

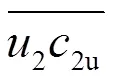
水泵；混流式水輪機；流線相似法；結構常數；沖擊損失；歐拉方程

0 前言

水力機械如水泵和水輪機的水動力特性曲線是由能量定理決定的。由于能量的轉換是伴隨著流動發生的，所以，流動損失直接削弱著水力機械內的能量交換。流動損失通常被視為水力機械的內在損失，并與流量即水力機械的工作點有關。在設計工況下，流動損失最小，能量轉換效率最大。在非額定工作點，流動損失通常由各種不同的局部損失引起。就水泵而言，局部損失之一是轉子進口處的沖擊損失。該損失發生在任何偏離額定工作點的工況下。在顯著的低負荷下，單一的沖擊損失還將轉化為脫流甚至旋轉脫流損失[1]。雖然這種局部損失早已為人們所熟知，并有各種描述與模擬計算。但是在嚴格的理論計算方面，一直以來都沒有突破性進展。同樣的局部損失發生在混流式水輪機轉子出口。任何偏離額定工作點的流動，都會導致水流在水輪機轉子出口包含有旋轉分量。由于該處流速的不均勻分布，人們還從來沒有找到一種準確的方法用于計算水流的旋轉分量以及由此決定的歐拉方程中出口項的平均值。同樣，包含于旋轉水流中的旋轉動能也無從計算。這方面的大量研究更多地則是集中在尾水管中流速分布，空化渦帶形成以及由此引發的壓力脈動等問題上，如文獻[2,3]。

這里折射了水泵與水輪機轉子低壓截面上局部損失的計算問題。

且以水泵為例。轉子各葉片通道進口處水流速度的不均勻分布是由流線彎曲引起的。其不均勻程度大都無法直接計算。所謂流線曲率法[4-6]雖然是基于文獻[7]中的一般理論開發而來的，并主要應用于渦輪壓縮機。但在用于水泵方面，則依然是通過反復迭代對微分方程進行計算的，還常常出現計算不收斂的情況。其它有效方法就是通過實驗做直接測量[8,9]。雖然計算流體力學在一定程度上能對該不均勻速度分布進行數值模擬計算，而且在以往的工程實踐中也的確發揮了一些作用。但是，就所述水泵進口處這一具體流動而言，它還不如流線曲率法適用。此外，很多數值模擬通常偏頗地將水泵內一些不佳的流動現象歸結為僅與轉子出口處流動狀況有關，即認為是由轉子和導向葉片之間的相互作用引起的[10-12]。總之，這里反映的是計算方法的問題。本文所要展示的，是如何將微分方程計算轉換為積分計算。這是一個嶄新且非常有效的分析計算方法，即流線相似法。其理論基礎是流動的勢流特征以及轉子入口處流線分布的幾何特性。

1 水泵轉子入口結構常數與流速分布

1.1 沿流線運動方程及流動的勢流特征

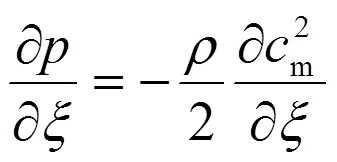
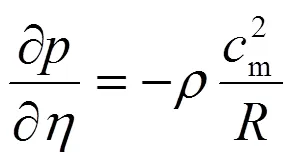
其中，是流線的曲率半徑。

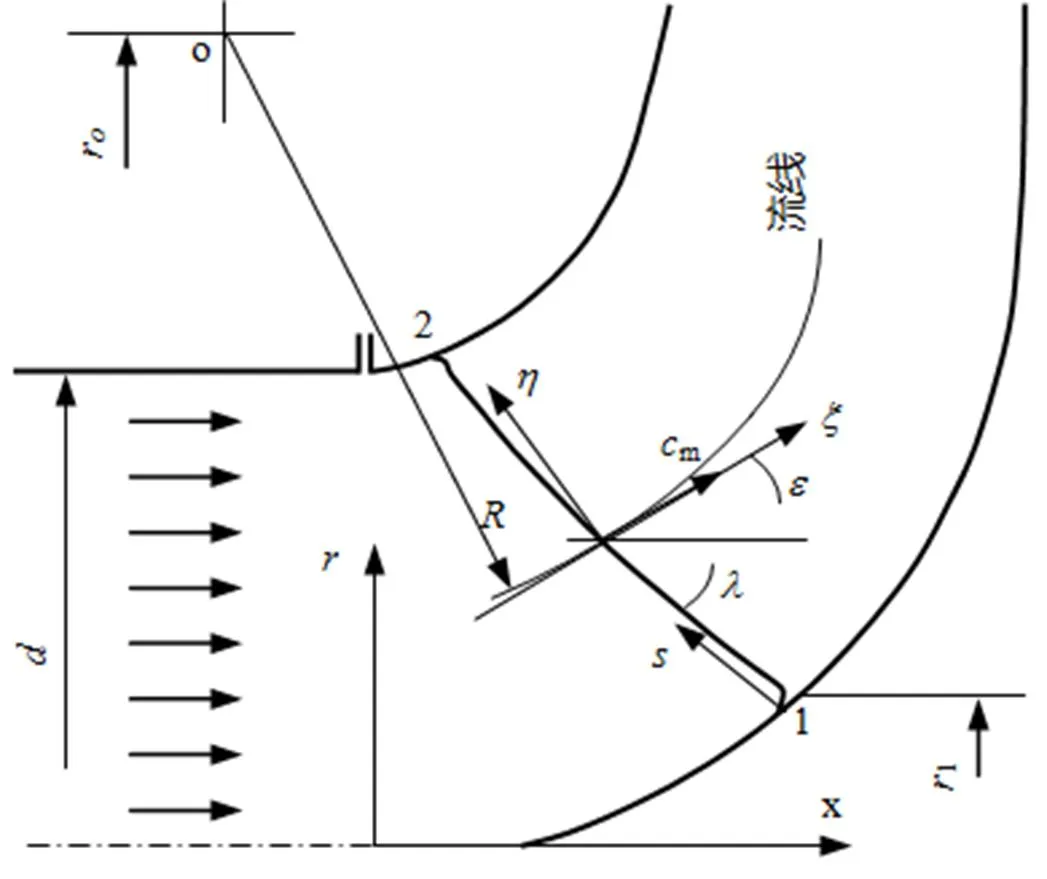
圖1 水泵轉輪子午面內的速度分布與各計算參數表示

另一方面，由于水泵吸水管內的直線流動通常可被看成是均勻分布，所以流動是無旋的有勢流動。在忽略粘性磨擦力影響的前提下，流體在到達并流經轉子葉片前緣時必然保持其勢流特征，即總壓力保持不變：

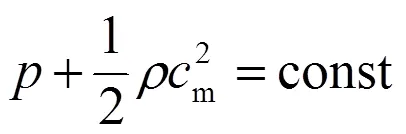
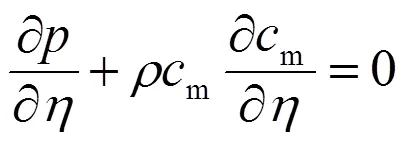
將式（2）代入后又得:

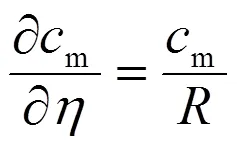
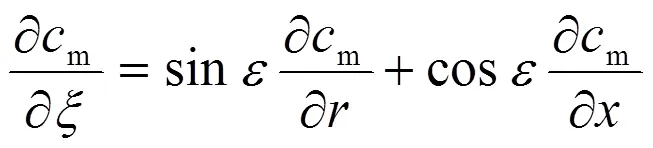
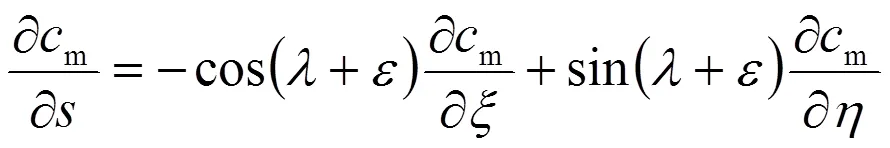
將式（5）帶入式（7）得：

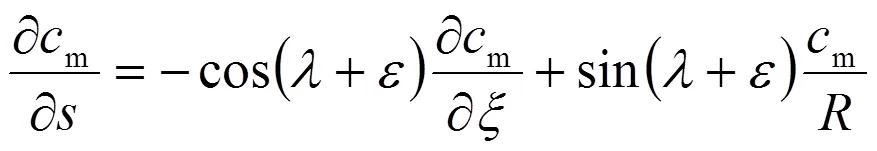
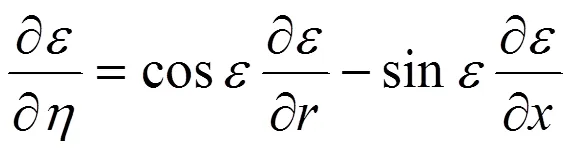
上列各式將在下面各計算中相繼得到應用。其中，/為一純幾何量，由流線分布決定，與流速無關。

1.2 連續方程

圓柱坐標系中的連續方程為

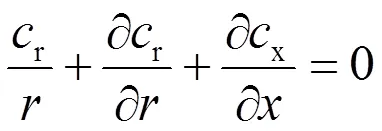
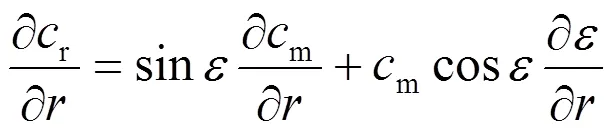
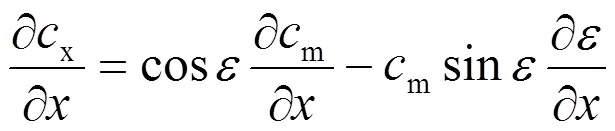
帶入式（10）得：

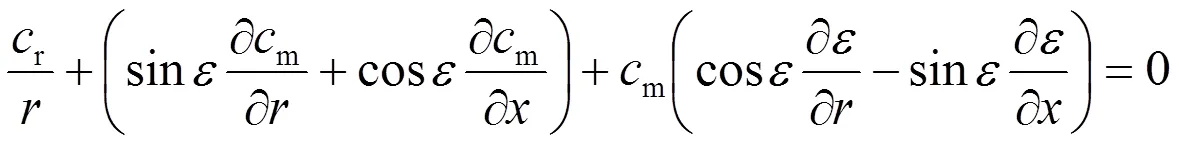
考慮到式（6）和式（9）得：

該式中對幾何量?/?的計算將在附錄中給出。

1.3 轉子進口速度分布與第一結構常數

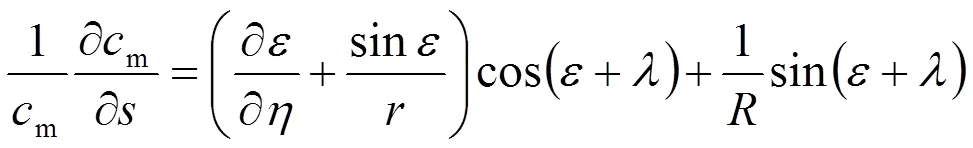
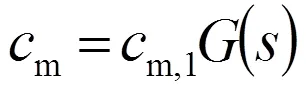
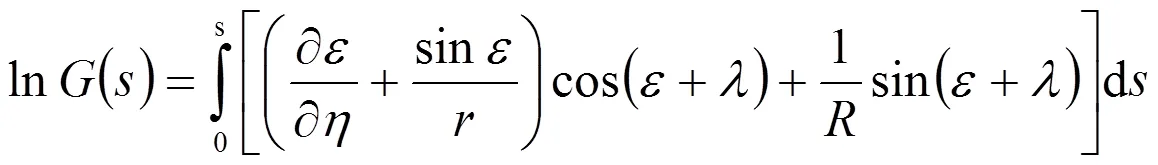
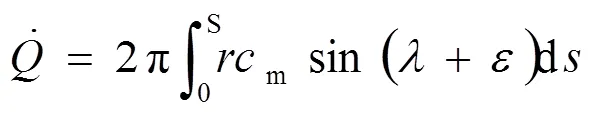
將式（15）代入后得

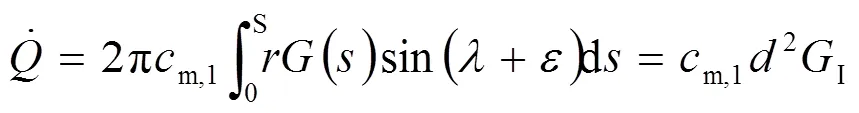
然后有

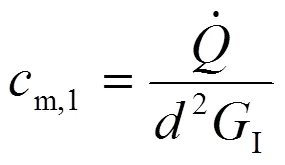
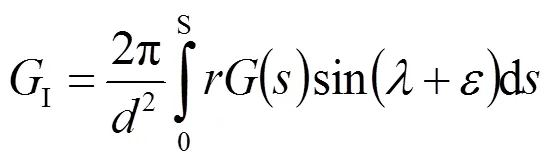
轉子進口處的速度分布最終可以表示為：

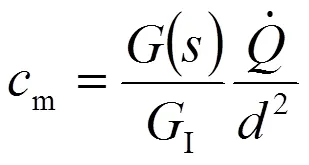
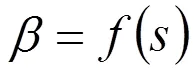
在不發生明顯脫流的情況下，式（21）適用于任何非額定流量。很明顯，子午面內的速度分布是由幾何分布()決定的。()所體現的是流線分布的相似性。所以，以此為基礎的計算方法稱為流線相似法。

1.4 特殊情況

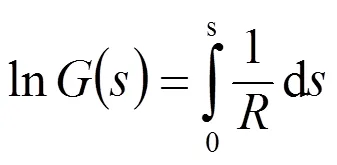
以及

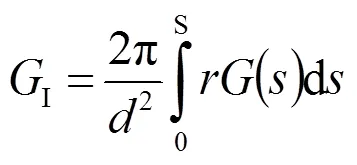
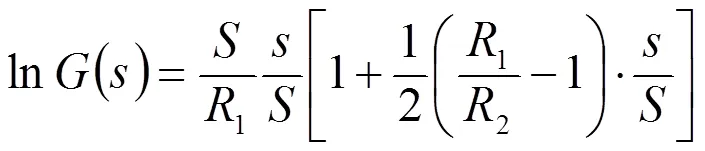
假設。然后，對于不同的由上式計算出的幾何參數G(s)以及它的分布如圖2所示。

由于幾何參數()直接反映了轉子進口處的流速分布，見式（15）和（21），圖2中的各曲線事實上反映了流速分布的比例。其中比值1/2從1.8到2.4的變化是根據文獻[13]選定的。很明顯，沿轉子葉片前緣的速度變化是極為顯著的。其差別達兩倍之多。這一計算結果既與流線曲率法的計算結果一致[4-6]，還與早期實際觀察相符[14]。在設計轉子葉片的走向時，這一不均勻流速分布必須予以考慮。

1.5 轉子進口壓力分布

除了速度分布由式（21）給出之外，相應的壓力分布可由式（3）直接給出如下：

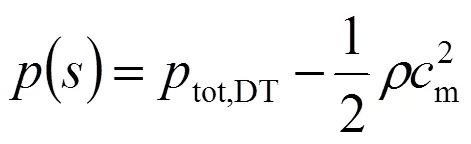
1.6 速度分布計算舉例

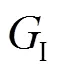
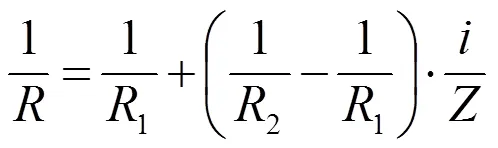
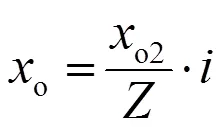
這里有=0, 1, 2, …。

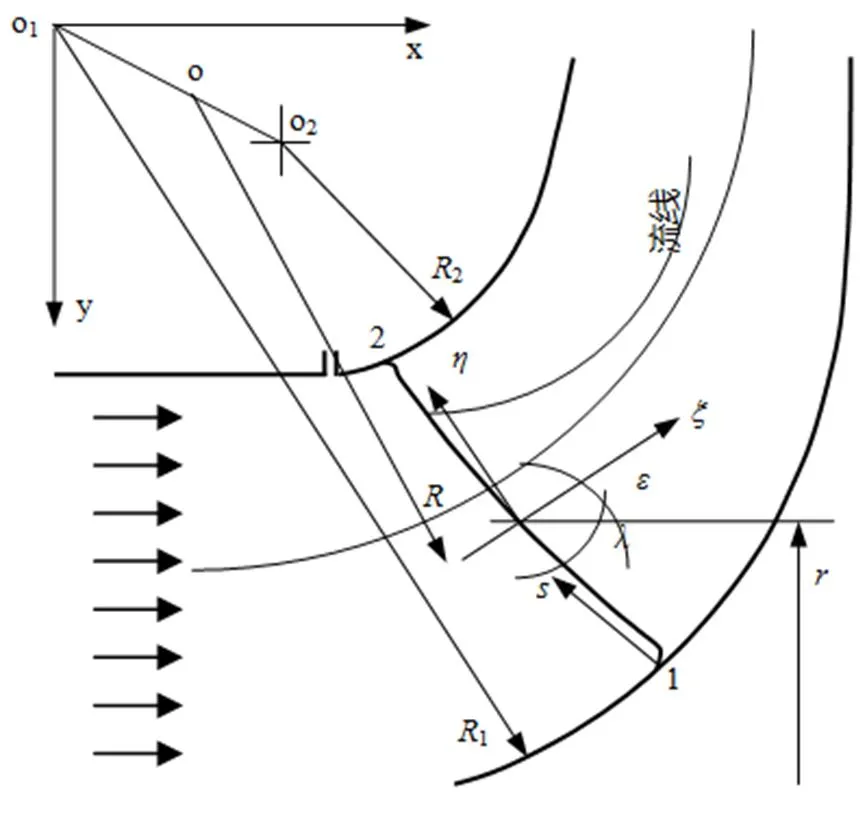
圖3 流線曲率與曲率中心的內插值計算

在坐標系，以o為曲率中心的第條流線可由圓方程表示，即

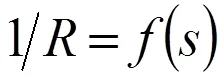
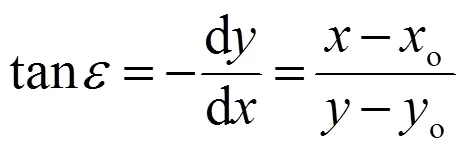
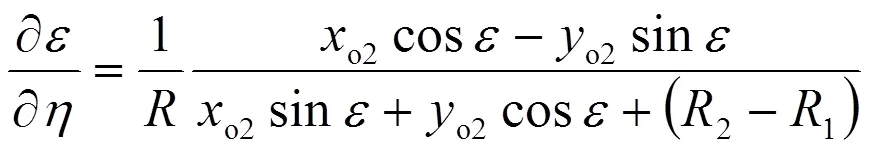
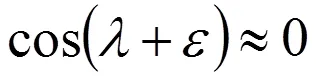
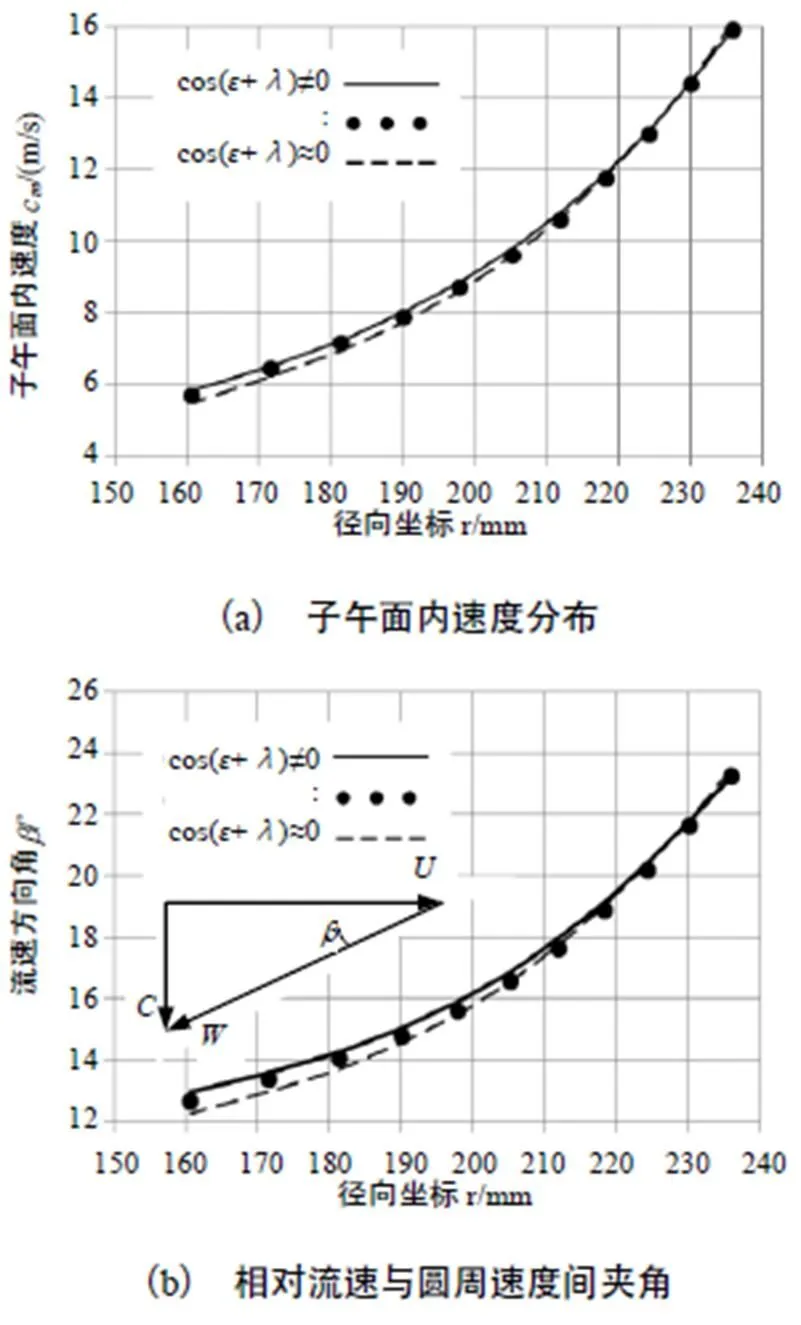
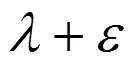
如同圖2所揭示的那樣，這里再一次顯示了轉子進口處流速分布的高度不均勻，且與文獻[14]中（圖126）所給出的流速變化相似（從2.5~6m/s）。

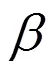
1.7 速度分布的實驗驗證

圖5示出了計算與本文作者協同事早期試驗結果[9]的比較。其中計算結果系采用式（21）和（24）。此外，圖中還比較了用指數函數表達的近似計算。此指數函數暫且適用于比轉速（n）為30~35的水泵。

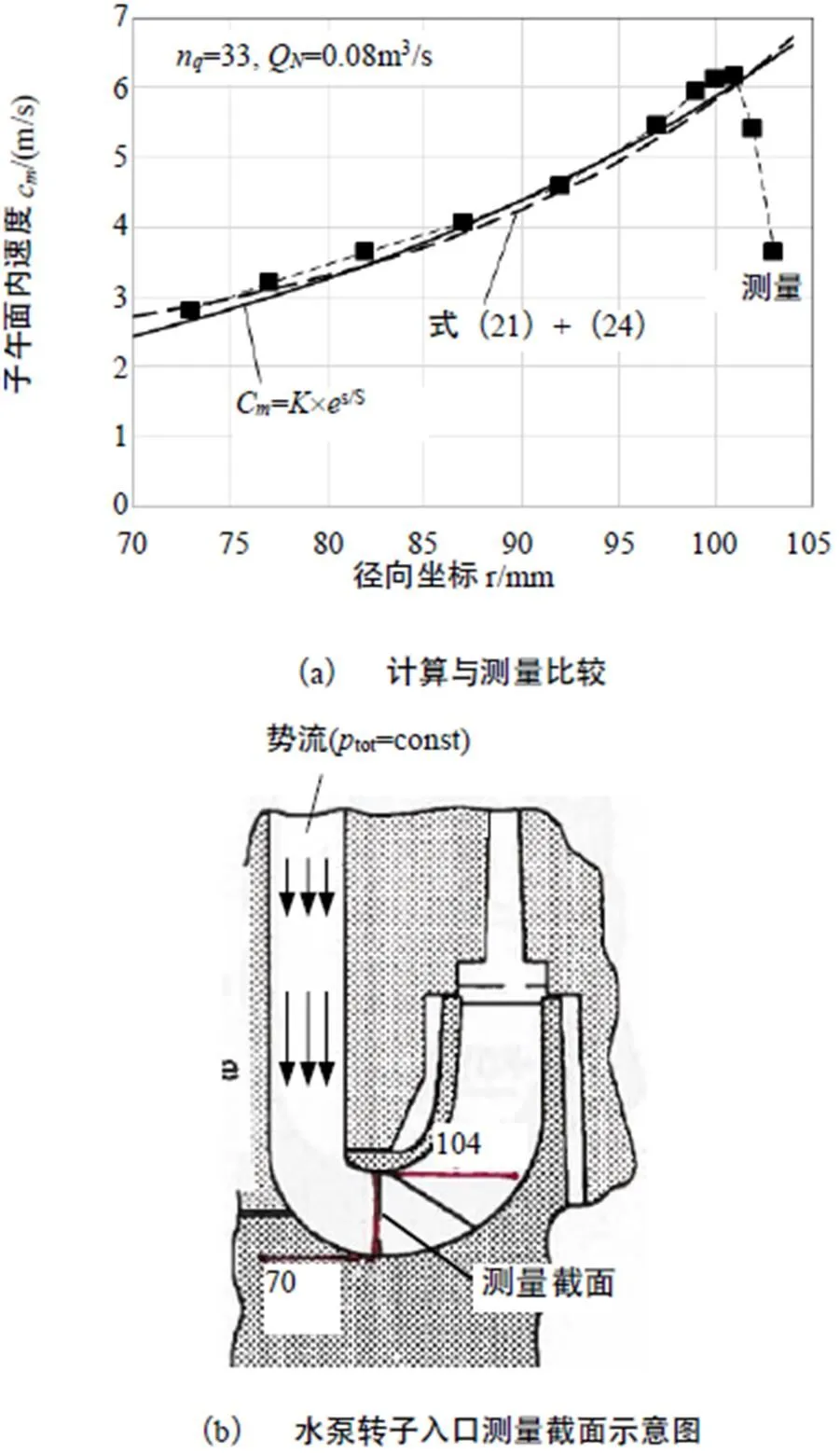
圖5 計算與試驗測量的比較。

注：測量取自文獻[9]。計算由式（21）和（24）而得

1.8 轉子入口沖擊損失與第二結構常數

由轉子進口流速分布可以計算出流體相對速度以及流向角，如圖4（b）所示。水泵導葉的設計是要保證在額定工況下(用下標N表示)導葉走向在進口處與流體流向角一致，從而保證不發生沖擊損失。所以，水泵導葉的傾角及其沿葉片前緣的分布可根據式（21）由下式計算：

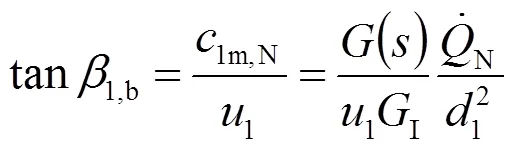
這里下標1表示轉子進口。此外，圓周速度（1=2π）是徑向坐標的函數。其它流動與幾何參數由圖6給出。下面的各計算，均假設轉子葉片的傾角及其分布按式（31）給定，即為已知。

在其它流速下，相對流向角由下式表示：

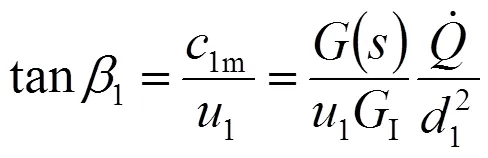
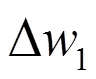
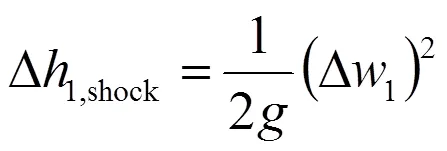
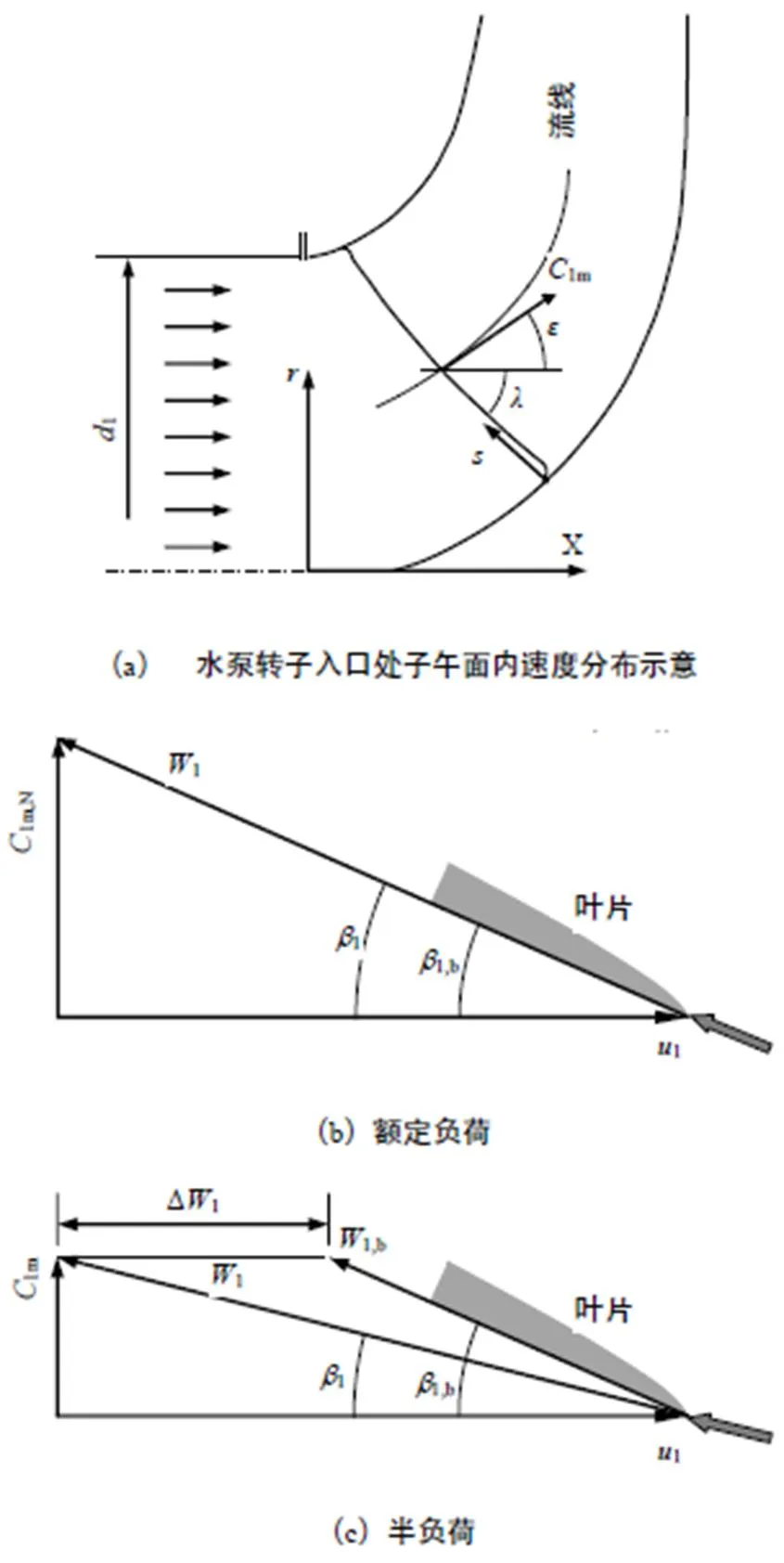
圖6 水泵轉子進口速度三角形以及沖擊損失計算

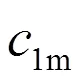
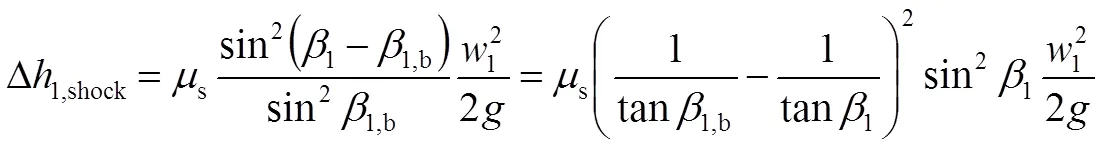
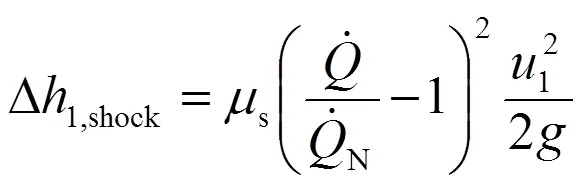
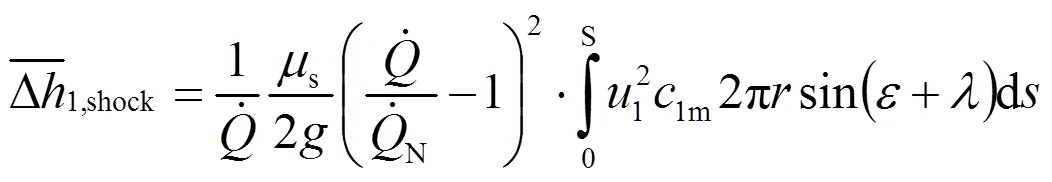
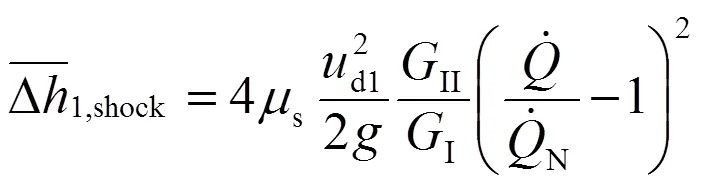
或

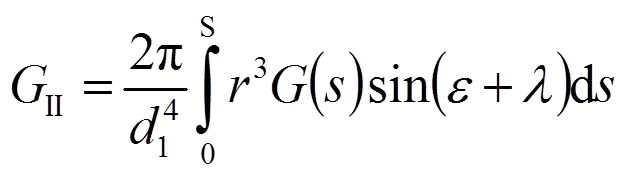
式（38）中，為水泵轉子進口處綜合結構常數，簡稱結構常數，其計算如下：

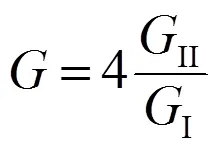
該結構常數歸根到底是由轉子進口處葉片前緣的幾何尺寸與位置決定的。它不僅在水泵計算中起著關鍵作用，而且還在混流式水輪機計算中從根本上決定著能量交換的計算精度。

2 混流式水輪機轉子出口結構常數與歐拉方程應用

混流式水輪機轉子出口的流動與水泵轉子進口的流動有其共性。在額定工況下，水輪機轉子出口的流動沒有旋轉分量。由于尾水管中的流動可近似地認為是均勻的直線流動，即有勢流，所以流體在轉子出口的流動也必然為有勢流。其速度沿葉片尾緣分布必然滿足式（21），即（下標2表示水輪機出口）：

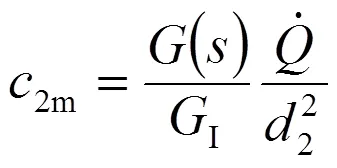
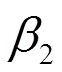
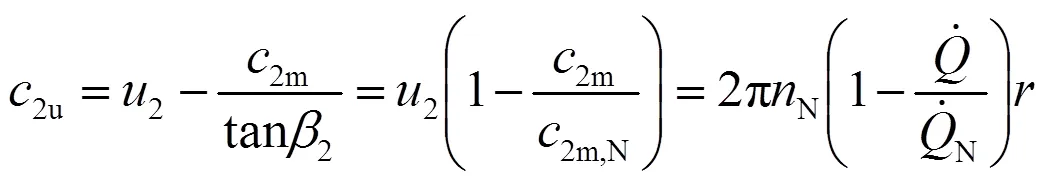
為了較準確地反映實際速度分布，上式中還可以根據情況引入一個修正系數。

在用歐拉方程計算單位流體做功的時候，在轉子出口，葉片尾緣截面上相應的項要用平均值，即

對出口平均值的計算首先根據圖1（這里水泵的入口被看作為水輪機的出口，用下標2表示）有下列積分：

（44）

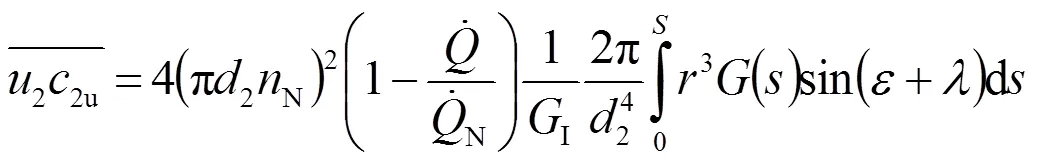
顯然，上式中的積分項是一個與流動無關的幾何量，且與式（39）計算相同，所以稱為混流式水輪機轉子出口第二結構常數。

考慮式（40），上式（45）最終可以寫成：

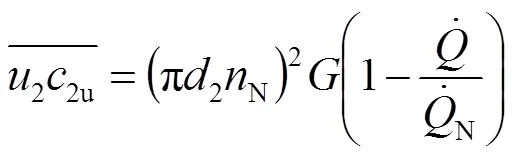
3 結束語

一直以來，水力機械如水泵和水輪機的水動力特性曲線大都是由試驗得來的。其分析計算的不可能，原因之一在于未能簡單而又準確地計算水泵入口處的速度分布。該速度分布不僅決定著額定工況下轉子葉片的設計，而且同時決定著非額定工況下轉子進口處的沖擊損失。該損失如此典型而且重要，卻向來都沒有被看重過，更無從計算。這是人們長期以來過于依賴試驗以及近年來又過于依賴計算流體力學(CFD)所造成的。

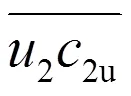
附錄: ?/?的計算

正文中，梯度分量?/?是決定流速分布的一個影響參數，具有幾何特性。

由式（9）并考慮?/?=-?/?則有：

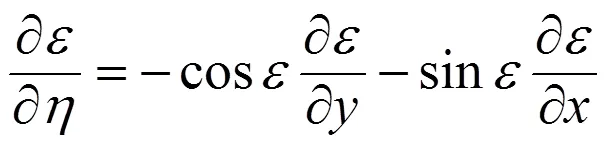
其中和坐標由圖3確定。

這樣，?/?的計算就歸結為?/?和?/?的計算。為此，流經計算點的流線按圖3由下列圓方程給出：

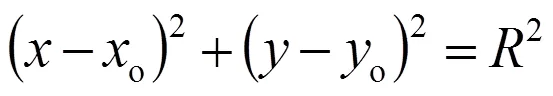
用圓弧段來表示局部流線，圓弧段的確定既包括圓弧段的中心還包括圓弧段的半徑。兩者均可通過在兩點o1與o2間做線性插值而得到。

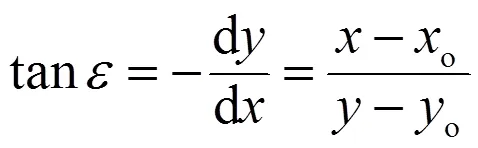
該式亦可寫為

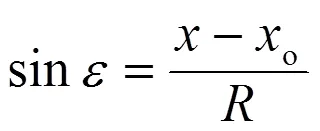
和

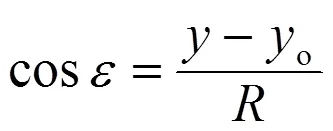
參數?/?和?/?將分別計算如下。

由式（a4）得:

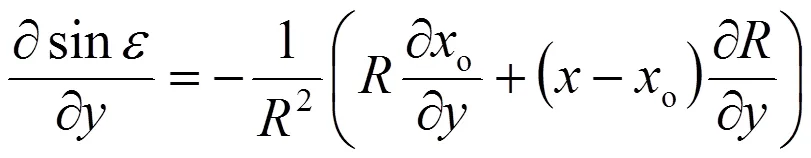
或可寫為

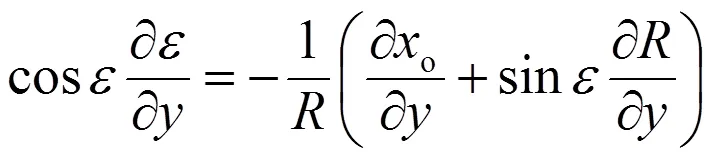
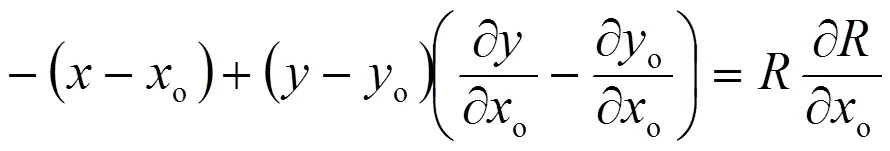
即

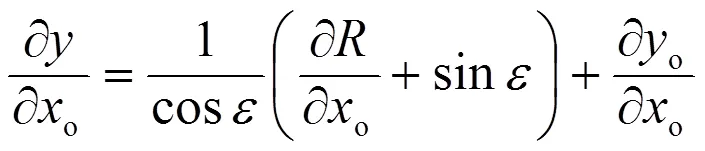
由式（a5）可得:

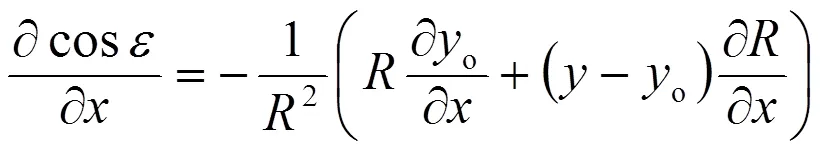
進一步得

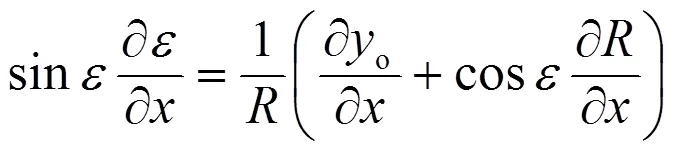
按同樣方式如（1）中，由式（a2）得到

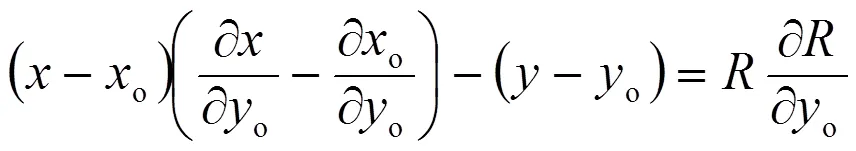
即

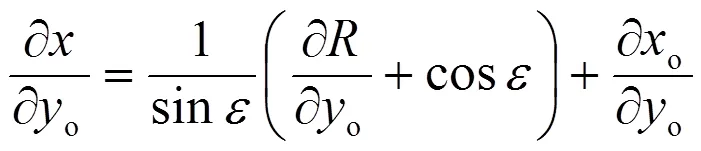
（3）聯立計算

式（a7）和式（a11）同時代入式（a1）。由此得

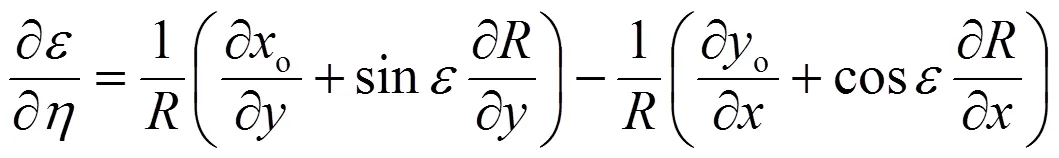
為了進一步簡化計算，可使用下述各關系式:

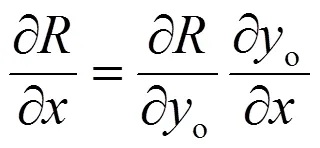
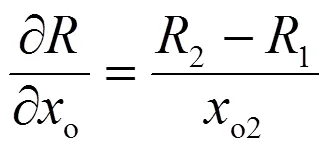
式（a9）和式（a13）同時代入式（a14）。最終得到

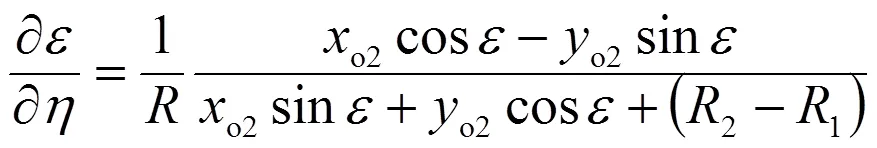
[1] Zhang, Zh..Rotating stall mechanism and stability control in the pump flows[J]. J. Power and Energy,2011, 225: 779-788.

[2] Susan-Resiga, R., Ciocan, G., Anton, I., Avellan, F.. Analysis of the swirling flow downstream a Francis turbine runner [J]., vol. 128, p177-189, 2006.

[3] Nielsen, TK., Olimstad, G.. Dynamic behaviour of reversible pump-turbines in turbine mode of operation [C]., Honolulu, 2010.

[4] Casey, M., Roth, P..A streamline curvature throughflow method for radial turbocompressors[C]. I. Mech. E. Conference C57/84. 1984.

[5] Casey, M.,Robinson,C.. A new streamline curvature throughflow method for radial turbo-machinery[J],132(3), 031021 (Apr 07, 2010).

[6] Gong, WQ., Wu, RK., Zhang, B..A new finite difference method to solve the velocity gradient equation in streamline curvature method[J]. Advances in Mechanical Engineering, 2016, 8(9): 1-13.

[7] Wu, CH.. A general theory of three-dimensional flow in subsonic and supersonic turbomachines of axial-, radial-, and mixed-flow types [R]. Washington DC, USA: NACA, 1952, NACA-TN-2604.

[8] Stoffel, B., Weiss, K.. Different types and locations of part-load recirculations in centrifugal pumps found from LDA measurements [C]., Valencia, Spain, 1996, II: 1034-1044.

[9] Eisele, K.. Global und LDA Messungen am Radialpumpenlaufrad La 033.112 mit unbeschaufeltem und beschaufeltem Diffusor[R]., IT 1773, 1992.

[10] Shi, F., Tsukamoto, H.. Numerical study of pressure fluctuations caused by impeller-diffuser interaction in a diffuser pump stage [J]., 2001, 123(3): 466-474.

[11]Muggli, F., Eisele, K., Zhang, Zh. et al.. Numerical investigations of the flow in a pump turbine in pump mode [C].,London, UK, 1999.

[12] Feng, J., Benra, F., Dohmen, H..Unsteady flow visualization at part-load conditions of a radial diffuser pump: By PIV and CFD [J]., 2009, 12(1): 65-72.

[13] Gülich, J.. Centrifugal pumps [M]. 2nd Edition, Berlin, Germany: Springer-Verlag,, (Fig. 7.4).

[14] Pfleiderer, K. Die Kreiselpumpen für Flüssigkeiten und Gase[M]. Springer Verlag, 1955, (Abb. 126).

[15] Zhang, Zh., Titzschkau, M.. Self-validated calculation of characteristics of a Francis turbine and the mechanism of the S-shape operational instability[C]., Beijing, China, 2012.

Structure Constant G and Streamline Similarity Method for Flow Distributions at the Low Pressure Sides of the Pump and the Turbine Impellers

ZHANG Zhengji, LI Zheng, WEI Xianzhu, QIN Daqing

(State Key Laboratory of Hydro-power Equipment (HILEM), Harbin 150040, China)

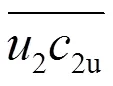
pump; Francis turbine; streamline similarity method; structural constant; shock loss; Euler equation

TK734

A

1000-3983(2018)01-0001-09