靜載與沖擊加載方式下滾刀破巖特性

譚青，勞同炳，張桂菊, 3，張旭輝，易亮，徐順生

?

靜載與沖擊加載方式下滾刀破巖特性

譚青1, 2，勞同炳1, 2，張桂菊1, 2, 3，張旭輝1, 2，易亮1, 2，徐順生4

(1. 中南大學 高性能復雜制造國家重點實驗室，湖南 長沙，410083；2. 中南大學 機電工程學院，湖南長沙，410083；3. 邵陽學院機械與能源工程學院，湖南 邵陽，422004；4. 湘潭大學 機械工程學院，湖南 湘潭，411105)

為了研究在單一恒定靜載荷和沖擊動載荷這2種情況下盤形滾刀破巖機制，使用顆粒離散元法建立滾刀破巖的二維數值模型。通過控制破巖的垂直載荷，對滾刀破巖動態過程進行分析并研究靜載荷、沖擊動載荷和沖擊次數對滾刀破巖特性的影響，最后通過實驗對靜載荷下滾刀破巖情形進行驗證。研究結果表明：在單一恒定靜載荷下，滾刀破巖效果隨著靜載荷增大而提高；當靜載荷達到一定值后，破巖效果提升不明顯，存在1個最佳靜載荷使破巖效果最優；在沖擊動載荷作用下，巖石裂紋擴展情況與靜載荷的擴展情況相似，但巖石內部以剪切破壞為主；隨著循環沖擊動載荷以及施加次數增大，巖石內部產生的裂紋數增大并且有向水平貫穿的趨勢，破巖比能耗先減少后變化不大；滾刀在動靜載荷作用下比能耗的變化趨勢基本一致，沖擊動載荷破巖的比能耗比靜載荷作用下的比能耗高，大約是靜載荷破巖比能耗的1.4倍。

滾刀；顆粒流；破巖特性；比能耗；靜載荷；沖擊動載荷

在地下掘進過程中，盾構刀具直接參與掘進破巖的工作，因此，研究盾構刀具切削巖石的特性、分析不同切削巖石的方法對于高效破巖的意義十分重大。到目前為止，國內外眾多學者對盾構刀具破巖機理開展了模擬建模和實驗分析。LIU等[1]采用二維有限元仿真軟件對滾刀侵入巖石過程進行了數值模擬，分析了巖石破碎過程的應力分布以及刀具的受力情況。劉建琴等[2]通過有限元軟件對盤形滾刀回轉破巖進行了仿真研究，優化設計了滾刀安裝參數。夏毅敏等[3?4]使用有限元軟件和離散元軟件模擬分析了切削過程中巖石的破碎過程和切屑的形成過程。MOON等[5]通過顆粒離散元法從刀間距和切深的角度，研究了滾刀的最佳破巖情況。楊岳峰等[6]通過建立刀頭沖擊模型研究了沖擊作用下巖石裂縫擴展情形。HUO等[7?8]通過動力學建模以及數值仿真對重載沖擊作用下盤形滾刀及刀盤的振動特性進行了分析，并研究了滾刀切削過程的力學特性。金解放等[9]利用巖石動靜組合加載霍普金森桿試驗裝置研究了不同軸壓的巖石在循環沖擊過程中動態強度和變形特性。趙伏軍等[10]介紹了其自行設計研制的多功能動、靜態耦合載荷破巖試驗系統并且通過試驗分析研究了動靜載荷耦合破巖具體形式。上述研究成果對于研究盤形滾刀破巖機理有很大的參考價值，但對于靜載荷與沖擊動載荷作用下盤形滾刀破巖形態這一方面的研究往往局限于試驗研究，而利用軟件建模配合實驗研究較少，且試驗研究很難從微觀角度觀察到滾刀在載荷作用下的破巖效果。離散元技術可以從微觀層面觀察揭示其破巖機理，對于研究滾刀在靜載荷和動載荷作用下的破巖機理具有重要意義。為此，本文作者在簡化滾刀破巖過程的基礎上，將刀圈運用球體Clump模型代替剛性墻模型[11]建立載荷邊界條件下盤形滾刀破巖的離散元模型，并對模擬仿真結果進行分析，研究滾刀在不同載荷形式作用下的破巖形式。

1 盤形滾刀破巖數值模型

1.1 巖石數值模型的確定

在利用顆粒流程序建立模型過程中，顆粒流的細觀參數需要一個標定過程使得其與材料的宏觀物理力學參數一一對應。在一般情況下，通過單軸壓縮和巴西劈裂數值試驗對模型參數進行標定[12]。實驗所使用的巖石來自廣東省佛山市某采石場，按照巖石力學試驗性能測試的標準制作了直徑為50 mm、高為100 mm以及直徑為50 mm，高為50 mm的圓柱試樣以及邊長為70 mm的正方體巖石試樣。并對巖石試樣幾個端面進行打磨，使其垂直度和平行度均達到測試要求，對巖石的試樣力學參數進行測試，得到巖石的力學性能參數如表1所示。

表1 硬巖材料宏觀參數

在巖石試樣數值模型模擬過程中，設定模型中的最大和最小顆粒半徑之比為1.66，其中最小顆粒半徑為8×10-4m。考慮到顆粒與顆粒之間存在孔隙，設定顆粒的密度為3.145 t/m3。在二維模型參數標定過程中，選取巖石試樣尺寸為長×寬為100 mm×50 mm。

基于巖石試樣力學試驗性能測試，在顆粒流程序軟件中對盤形滾刀破巖中的巖石進行單軸壓縮和巴西劈裂的數值模擬，經過不斷標定選取合適的細觀參數去匹配表1中的宏觀參數，得到此時巖石試樣在PFC2D中的細觀參數如表2所示。

表2 細觀力學參數

1.2 滾刀載荷加載侵入破巖數值模型簡化

隨著盾構機刀盤的旋轉與推進，盤形滾刀一方面在切向摩擦力的作用下作滾動運動，另一方面在刀盤推力作用下作直線侵入運動[13]。在盤形滾刀破巖過程中，巖石裂紋的產生與擴展的主導因素是主推力作用下的侵入運動。INNAURATO等[14]的研究都是通過二維的平面等效方式進行，將盤形滾刀破巖簡化為侵入破巖過程，其研究成果表明將盤形滾刀破巖簡化成二維侵入破巖的問題是可行的。基于此，本文主要研究盤形滾刀在推力作用下巖石內部裂紋的產生及擴展過程，將滾刀破巖問題簡化為二維侵入問題。

滾刀破巖數值模型如圖1所示，巖石的長×寬為300 mm×160 mm，根據滾刀刀圈的結構特性以及軟件中剛性墻無法施加推力載荷的條件，在建模過程中滾刀采用球體clump模型代替。通過賦予滾刀clump單一恒定載荷和循環沖擊動載荷等不同的推力載荷形式，盤形滾刀往下運動并逐步侵入巖石，模擬滾刀在不同載荷形式作用下的破巖形式，觀察巖石內部裂紋萌發與擴展情況。其中滾刀沖擊動載荷波形采取實驗室常見的矩形波[15]，加載時間為24 μs。

圖1 滾刀破巖數值模型

2 滾刀在不同恒定靜載荷下破巖規律

2.1 滾刀在不同恒定靜載荷下數值模擬

靜載荷/ kN：(a) 20；(b) 26；(c) 32；(d) 38；(e) 44

從圖2可見：當盤形滾刀以不同的靜載荷侵入巖石中時，巖石內部同時存在剪切裂紋和張拉裂紋，整體表現為拉壓復合破壞；當靜載荷較小時(見圖2(a))，盤形滾刀不能有效地侵入巖石，只能在巖石表面形成一些微小裂紋，甚至只發生彈性變形，破碎效果極差；當靜載荷逐步增大時，巖石內部中間裂紋和側向裂紋長度明顯增大，破碎區域向巖石深部發展，側向裂紋長度的增大速度高于中間裂紋長度的增大速度(見圖2(b))；當靜載荷增大到一定程度時(見圖2(c))，巖石側向裂紋往巖石自由平面發育，形成大體積破碎塊，巖石破碎體積增到最大；當靜載荷繼續增大時，巖石內部的側向裂紋與自由平面形成貫通，巖石破碎體積得不到明顯增大，且滾刀下方發生過度破碎，消耗能量也過多，巖石破巖效果并不隨之提高(見圖2(d)和圖2(e))。

盤形滾刀的破巖比能耗定義為刀具切削單位體積巖石所消耗的能量[17?18]，是表征破巖效率的重要參數，破巖比能耗越小，說明盤形滾刀破巖效率越高，其具體表達公式如下：

式中：為破巖比能耗；N為垂直力；為刀具破巖消耗的能量；為貫入度；為巖石破碎體積，=；為破碎面積之和，根據裂紋的擴展情況測量；為單位厚度。

在靜載荷作用下，滾刀破巖裂紋長度、破碎體積、比能耗隨靜載荷變化關系如圖3所示。從圖3可見：當滾刀靜載荷低于32 kN時，巖石內部產生的側向裂紋長度與中間裂紋長度增長速度較大，裂紋分布的深度與其水平貫通面積也隨之增大，破碎體積明顯增大，滾刀破巖比能耗降低；當滾刀靜載荷超過32 kN時，巖石內部裂紋長度增長不明顯，破碎體積得不到明顯增大，破巖比能耗變化不明顯，反而有所上升，此時，靜載荷增大值對巖石破碎效果影響不大；當靜載荷為32 kN時，盤形滾刀比能耗最小，其值為9.33 MJ/m3，此時，盤形滾刀在靜載荷作用下破巖效果最優。

(a) 靜載荷與裂紋長度的關系；(b) 靜載荷與比能耗和破碎體積的關系

2.2 滾刀在不同恒定靜載荷下的實驗研究

通過直線式盤形滾刀破巖實驗臺進行盤形滾刀破巖實驗研究。實驗裝置由機架、水平工作臺、液壓系統和電控測試系統共4部分構成，整個實驗臺由液壓系統進行驅動，盤形滾刀上下直線運動由垂直液壓缸驅動，巖石縱向進給由縱向液壓缸驅動。

實驗時，將盤形滾刀安裝于刀架上，并將盤形滾刀調至實驗巖石正上方，通過垂直液壓缸加載裝置對滾刀施加垂直力，通過縱向液壓缸控制工作臺的前后移動，從而使得滾刀滾壓切削巖石。實驗滾刀使用常截面滾刀，直徑為432 mm，刀刃寬為18 mm，刀刃角為20°。巖石力學參數如下：抗壓強度為100.33 MPa，抗拉強度為5.69 MPa，彈性模量為11.45 GPa。由于實際的破巖總會出現巖石的階躍式破壞，而滾刀上受到的力不會實現恒定，但通過設定實驗臺垂直油缸的油壓推力使得整個過程滾刀受力在一定靜載附近上下波動，近似為恒定載荷破巖。試驗中，垂直油壓分別選取6，7和8 MPa進行多組驗證試驗。

在靜載荷作用下，滾刀破巖實驗過程如下：首先，盤形滾刀在不同垂直載荷下侵入巖石；接著，控制實驗臺縱向油缸使得巖石向前運動而進行滾刀滾動切削實驗。每次實驗切削結束后，使用帶百分表的游標卡尺測量滾刀侵入深度，量取不同點切削槽的寬度并取平均值，并測量統計破碎塊的尺寸。使用攝像機觀察記錄滾刀侵入巖石時破碎坑的形狀，統計滾刀侵入巖石破碎坑的體積。

在靜載荷破巖試驗中，在不同靜載荷下，巖石破碎坑與破碎塊的尺寸和形狀均有所不同，滾刀的貫入度也不一樣。在切削過程中，較大的靜載荷能促進巖石裂紋擴展，使得中間裂紋以及側向裂紋增長，從而導致巖石的破碎坑寬度增大，貫入度增大。所以，當靜載荷增大時，巖石破碎坑增大，滾刀的貫入度也隨之增大，被剝落的巖石碎屑增多。實驗結果如表3 所示。

(2)With increasing number of the epochs,the errors in the carrier IAR decreased.

表3 不同的靜載荷模型最終實驗結果

從表3可見：當靜載荷逐步增大時，滾刀的貫入度增大，巖石破碎坑體積與破碎坑的寬度也隨之增大，但增長速度減緩，與模擬仿真變化趨勢一致，驗證了模擬仿真結果的可靠性。

3 滾刀在沖擊動載荷下破巖規律

3.1 滾刀在沖擊動載荷下受力規律

為了實現盤形滾刀靜載荷和沖擊載荷的衡量標準，使得滾刀加載靜載荷與加載沖擊動載荷消耗的能量相等，便于后續破碎效果比較，以能產生與靜載荷作用時消耗能量相等的沖擊載荷作為當量沖擊載荷，并以此作為矩形波沖擊載荷的峰值。產生此沖擊載荷消耗的能量可由沖擊桿動能推算得到。當滾刀分別在靜載荷與矩形波沖擊載荷作用下進行破巖時，通過觀察比較靜載荷與沖擊動載荷的破巖情況，并計算各自的比能耗，比較兩者的破巖效果。實驗臺的沖擊加載設備簡化圖如圖4所示。

圖4 盤形滾刀沖擊破巖受力示意圖

滾刀與巖石相互作用下及滾刀在沖擊動載荷作用下，其侵入微分方程的一般形式[19]為

式中：為沖擊動載荷的侵入載荷；為侵入系數；為滾刀的平均波阻；()為滾刀沖擊后承受的沖擊載荷函數；為時間。在=0時，=0 N，解式(2)可得

考慮到沖擊桿跟滾刀相互作用下，將沖擊桿看成剛體，不考慮撞擊面的變形，當初始條件為=0 s時，沖擊桿速度=0，按照牛頓定律與一維應力波原理可得

式中：為沖擊桿質量。將式(4)代入式(3)得

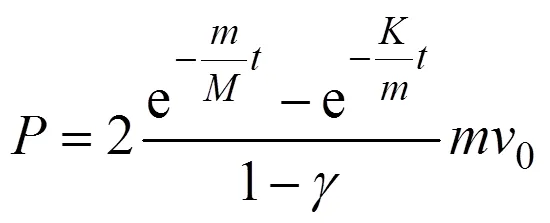
式中：=2/()；為撞擊侵入指數，為量綱一的量。

可求得最大侵入力為

結合沖擊破巖時消耗的動能為02/2，假定靜載力破巖消耗的能量與沖擊破巖消耗的能量一樣，當量沖擊載荷為最大侵入力的一半，則可得當量沖擊載荷與靜載荷作的功的關系如下：

3.2 滾刀在沖擊動載荷下破巖規律

從圖5可見當盤形滾刀以不同循環沖擊載荷侵入巖石中時巖石內部的裂紋分布情況。對比于靜載荷破巖情況，巖石內部滾刀下面的區域主要是剪切裂紋，以壓破壞為主，而巖石內部的側向裂紋主要由拉破壞所致；當沖擊次數一樣時，巖石的貫入度隨著沖擊動載荷的增大而增大，巖石內部產生的裂紋數目也隨之增大，巖石內部的側向裂紋得到擴展，并趨向于巖石的自由平面，有利于形成較大的破碎塊，降低盤形滾刀破巖的比能耗，提高破巖效率。從圖6可見：當巖石沖擊動載荷峰值由264 kN變化到360 kN時，滾刀的貫入度由3.33 mm增大到4.21 mm，巖石內部側向裂紋長度由39.55 mm增長到67.88 mm，巖石內部中間裂紋長度由53.48 mm增長到75.12 mm。觀察圖5(a)和圖5(b)可見：在沖擊載荷峰值的增量一樣時，巖石內部側向裂紋的擴展長度比中間裂紋擴展長度大。這是由于在盤形滾刀破巖過程中，沖擊動載荷增大能促進巖石內部的側向裂紋發育，導致巖石產生大體積破碎塊，而巖石內部在滾刀貫入部位形成大面積破碎粉末，產生的中間裂紋不能得到有利發育。當單純地提高沖擊動載荷時(據圖5(c)和圖5(d))，巖石在高沖擊動載荷的作用下，貫入度和破碎體積稍增大，但效果并不顯著。從圖5(a)也可看出：當沖擊動載荷增大時，貫入度和破碎體積變化曲線的斜率變小，貫入度和破碎體積增大效果不明顯。另外，對比圖5(e)，(f)，(g)和(h)中盤形滾刀沖擊動載荷破巖情形，當沖擊載荷不變時，隨著沖擊次數增大，滾刀破巖各參數量變化趨勢大致與增大沖擊載荷的變化趨勢一樣，如圖6所示。表4給出了各組沖擊動載荷破巖模型的滾刀破巖比能耗。從表4可見：比能耗隨著沖擊動載荷的增大先減少再增大。而當沖擊動載荷施加的次數增大時，巖石在高沖擊動載荷的作用下，其內部已經形成過破碎，從而導致巖石反復破碎，消耗的能量也會過多，容易導致能量耗散，因此，沖擊動載荷沖擊次數對于破巖效果提高影響不大，比能耗反而增大。

(a) P沖=264 kN (n=4)；(b) P沖=312 kN (n=4)；(c) P沖=336 kN (n=4)；(d) P沖=360 kN (n=4)；(e) n=2 (P沖=312 kN)；(f) n=4 (P沖=312 kN)；(g) n=6 (P沖=312 kN)；(h) n=8 (P沖=312 kN)

(a) 沖擊載荷與破碎體積跟貫入度的關系；(b) 沖擊載荷與裂紋長度的關系；(c) 沖擊次數與破碎體積跟貫入度的關系；(d) 沖擊次數與裂紋長度的關系

表4 不同的沖擊動載荷模型最終比能耗

4 靜載荷與沖擊動載荷破巖效果比較

沖擊作為一種及其簡單的破巖手段，相對于靜載荷，其能在較短時間獲得很大的力，能夠使巖石內部瞬間萌發大量裂紋，為后續破巖打下了有利基礎。在沖擊動載荷作用下，巖石的侵入硬度和強度都有所提高，滾刀破巖比能耗相對于靜載荷作用較高。BAKER等[20?21]通過對玻璃、瓷器和水泥砂漿試塊進行強度測試試驗，發現抗壓強度和抗拉強度的倒數與加載時間的對數呈線性關系；隨著加載時間減少，物體強度隨之增大，這對滾刀破巖有利。在滾刀破巖過程中，分別比較在靜載荷為26，32，38和44 kN，及相對應的當量沖擊動載荷分別264，312，336和360 kN作用下的4組硬巖破巖比能耗，結果見圖7。

1—靜載荷；2—動載荷。

從圖7可見：對于此種硬巖，滾刀在動、靜載荷作用下比能耗的整體變化呈下降趨勢；滾刀破巖的比能耗都隨著靜載荷或動載荷增大而減低，變化趨勢近似一致；純沖擊動載荷破巖的比能耗都高于靜載荷作用下的比能耗，相對應動靜載荷比能耗的比值均值約為1.4，單純的沖擊動載荷并不能有效地提高破巖效率。

5 結論

1) 隨著靜載荷增大，巖石破碎體積和側向裂紋長度先增大后趨于不變，破巖比能耗先減少后有所上升，當靜載荷為32 kN時破巖效果最優。

2) 當靜載荷逐步增大時，滾刀貫入增大，巖石破碎塊體積與破碎坑的寬度也隨之增大，但增長速度減緩，與模擬仿真變化趨勢一致。

3) 在矩形波沖擊動載荷作用下，巖石裂紋擴展情況與靜載荷的擴展情況相似。當峰值及施加次數增大時，滾刀貫入度隨之增大，裂紋長度增大且有向水平貫穿的趨勢，巖石破碎體積增大，破巖比能耗減少。單純靠提高沖擊載荷或沖擊次數不能顯著提高破巖效率。

4) 滾刀在靜載荷和沖擊動載荷作用下，比能耗的變化趨勢基本一致，但沖擊動載荷破巖的比能耗比靜載荷作用下的高，大約是靜載荷破巖的1.4倍，故單純的沖擊動載荷并不能有效提高破巖效率。

[1] LIU H Y, KOU S Q, LINDQVIST P A, et al. Numerical simulation of the rock fragmentation process induced by indenters[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(4): 491?505.

[2] 劉建琴, 劉蒙蒙, 郭偉. 硬巖掘進機盤型滾刀回轉破巖仿真研究[J]. 機械工程學報, 2015, 51(9): 199?205. LIU Jianqin, LIU Mengmeng, GUO Wei. Research on the simulation of cutting rock rotary by hard rock tunnel boring machine disc cutters[J]. Journal of Mechanical Engineering, 2015, 51(9): 199?205.

[3] 夏毅敏, 薛靜, 周喜溫. 盾構刀具破巖過程及其切削特性[J]. 中南大學學報(自然科學版), 2011, 42(4): 954?959. XIA Yimin, XUE Jing, ZHOU Xiwen. Rock fragmentation process and cutting characteristics on shield cutter[J]. Journal of Central South University (Science and Technology), 2011, 42(4): 954?959.

[4] 譚青, 徐孜軍, 夏毅敏, 等. 2種切削順序下TBM刀具破巖機理的數值研究[J]. 中南大學學報(自然科學版), 2012, 43(3): 940?946. TAN Qing, XU Zijun, XIA Yimin, et al. Numerical study on mode of breaking rock by TBM cutter in two cutting orders[J]. Journal of Central South University (Science and Technology), 2012, 43(3): 940?946.

[5] MOON T, OH J. A Study of optimal rock-cutting conditions for hard rock TBM using the discrete element method[J]. Rock Mechanics and Rock Engineering, 2012, 45(5): 837?849.

[6] 楊岳峰, 梁正召, 唐春安. 沖擊作用下的壓頭破巖機制研究[J]. 巖土力學, 2013, 34(6): 1775?1785. YANG Yuefeng, LIANG Zhengzhao, TANG Chunan. Rock fragmentation mechanism induced by a drill bit subjected to dynamic loading[J]. Rock and Soil Mechanics, 2013, 34(6): 1775?1785.

[7] HUO Junzhou, SUN Xiaolong, LI Guangqing, et al. Multi-degree-of-freedom coupling dynamic characteristic of TBM disc cutter under shock excitation[J]. Journal of Central South University, 2015, 22(9): 3326?3337.

[8] 霍軍周, 歐陽湘宇, 王亞杰, 等. 重載沖擊激勵下TBM刀盤振動特性的影響因素分析[J]. 哈爾濱工程大學學報, 2015, 36(4): 555?559. HUO Junzhou, OUYANG Xiangyu, WANG Yajie, et al. Analysis of influencing factors of vibration behaviors of TBM cutterhead under heavy impact loads[J]. Journal of Harbin Engineering University, 2015, 36(4): 555?559.

[9] 金解放, 李夕兵, 殷志強, 等. 軸壓和循環沖擊次數對砂巖動態力學特性的影響[J]. 煤炭學報, 2012, 37(6): 923?930. JIN Jiefang, LI Xibing, YIN Zhiqiang, et al. Effects of axial pressure and number of cyclic impacts on dynamic mechanical characteristics of sandstone [J]. Journal of China Coal Society, 2012, 37(6): 923?930.

[10] 趙伏軍, 李夕兵, 馮濤, 等. 動靜載荷耦合作用下巖石破碎理論分析及試驗研究[J]. 巖石力學與工程學報, 2005, 24(8): 1315?1320. ZHAO Fujun, LI Xibing, FENG Tao, et al. Theoretical analysis and experiments of rock fragmentation under coupling dynamic and static loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(8): 1315?1320.

[11] 譚青, 張旭輝, 夏毅敏, 等. 不同圍壓與節理特征下盤形滾刀破巖數值研究[J]. 煤炭學報, 2014, 39(7): 1220?1228. TAN Qing, ZHANG Xuhui, XIA Yimin, et al. Numerical study on breaking rock by disc cutter at different confining pressure and joint characteristics case[J]. Journal of China Coal Society, 2014, 39(7): 1220?1228.

[12] MOON T, NAKAGAWA M, BERGER J. Measurement of fracture toughness using the distinct element method[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(3): 449?456.

[13] 劉建琴, 劉蒙蒙, 郭偉, 等. 隧道掘進機刀盤結構性能評價研究關鍵問題分析[J]. 現代隧道技術, 2014, 51(2): 5?10. LIU Jianqin, LIU Mengmeng, GUO Wei, et al. Analysis of key problems in the structural performance evaluation for TBM cutter heads[J]. Modern Tunnelling Technology, 2014, 51(2): 5?10.

[14] INNAURATO N, OGGERI C, ORESTE P P, et al. Experimental and numerical studies on rock breaking with TBM tools under high stress confinement[J]. Rock Mechanics and Rock Engineering, 2007, 40(5): 429?451.

[15] 廖志毅, 梁正召, 唐春安, 等. 動靜組合作用下刀具破巖機制數值分析[J]. 巖土力學, 2013, 34(9): 2682?2689, 2698. LIAO Zhiyi, LIANG Zhengzhao, TANG Chunan, et al. Numerical simulation of rock fracture mechanism induced by a drill bit under combined dynamic and static loading[J]. Rock and Soil Mechanics, 2013, 34(9): 2682?2689, 2698.

[16] 張旭輝. 圍壓與節理作用下滾刀破巖特性研究[D]. 長沙: 中南大學機電工程學院, 2015: 64?76. ZHANG Xuhui. The study of rock breaking characteristic by disc cutters under confining pressure and joint[D]. Changsha: Central South University. School of Mechanical and Electrical Engineering, 2015: 64?76.

[17] 茅承覺, 劉友元. 隧洞掘進機盤形滾刀滾壓巖石的試驗[J]. 工程機械, 1985(3): 21?26. MAO Chengjue, LIU Youyuan. Test on rolling rock by disc cutter of tunnel boring machine[J]. Construction Machinery and Equipment, 1985(3): 21?26.

[18] 霍軍周, 楊靜, 孫偉, 等. 不同模式下TBM刀群三維回轉切削仿真與優化設計[J]. 哈爾濱工程大學學報, 2014, 35(11): 1403?1408. HUO Junzhou, YANG Jing, SUN Wei, et al. Simulation and optimization design of three-dimensional rotating cutting action of TBM cutter group with different modes[J]. Journal of Harbin Engineering University, 2014, 35(11): 1403?1408.

[19] 徐小荷, 余靜. 巖石破碎學[M]. 北京: 煤炭工業出版社, 1984: 159?180. XU Xiaohe, YU Jing. Rock crushing study[M]. Beijing: China Coal Industry Press, 1984: 159?180.

[20] BAKER T C, PRESTON F W. Fatigue of glass under static loads[J]. Journal of Applied Physics, 1946, 17(3): 170?178.

[21] 鈴木光. 巖體力學與測定[M]. 北京: 煤炭工業出版社, 1980: 110?146. LIN Muguang. Rock mechanics and measurement[M]. Beijing: China Coal Industry Press, 1980: 110?146.

(編輯 陳燦華)

Disc cutter cutting mechanism under static loading and impact dynamic loading conditions

TAN Qing1, 2, LAO Tongbing1, 2, ZHANG Guiju1, 2, 3, ZHANG Xuhui1, 2, YI Liang1, 2, XU Shunsheng4

(1. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China;2. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;3. Department of Mechanical and Energy Engineering, Shaoyang University, Shaoyang 422004, China;4. School of Mechanical Engineering, Xiangtan University, Xiangtan 411105, China)

In order to research the disc cutter cutting mechanism under static loading and impact dynamic loading conditions, a two-dimensional numerical simulation method with which disc cutters break rock was established based on the particle discrete element method. Stress boundary condition was considered instead of velocity boundary condition. The dynamic process of breaking rock under constant static loading and impact dynamic loading was analyzed. The effects of load and impact cycle numbers on the characteristics of breaking rock were studied. Finally, an experiment was carried out on the linear experiment platform. The results show that the increase of static load can improve the rock fragmentation effects under constant static loading. When static load reaches a certain value, the rock fragmentation effects change inconspicuously and there is a optimal value which makes the rock fragmentation effects best. Under impact dynamic loading, the rock crack propagation behavior is similar to that under static loading, but the rock is prior to shear failure. With the increase of dynamic load and frequency, the number of rock cracks increases and the specific energy consumption decreases and then changes little. Meanwhile, the rock cracks tend to penetrate rock free surface. The variation trend of the specific energy consumption under constant static loading is consistent with that under cyclic impact dynamic loading and the former is 1.4 times of the latter.

cutter; particle flow; cutting characteristics; specific energy consumption; constant static loading; impact dynamic loading

TP391.9；U455.3+1

A

1672?7207(2018)01?0101?08

10.11817/j.issn.1672-7207.2018.01.014

2017?01?02；

2017?03?14

國家重點基礎研究發展計劃(973計劃)項目(2013CB035401)；國家高技術研究發展計劃(863計劃)項目(2012AA041801)；國家自然科學基金資助項目(51274252) (Project(2013CB035401) supported by the National Basic Research Development Program(973 Program) of China; Project(2012AA041801) supported by the National High Technology Research and Development Program(863 Program) of China; Project(51274252) supported by the National Natural Science Foundation of China)

張桂菊，博士研究生，副教授，從事巖石切削機理研究；E-mail: zhangguiju1999@sina.cn