基于主成分約簡和突變級數的艦載機出動能力綜合評估方法

夏國清, 欒添添, 孫明曉, 仲偉東, 劉彥文

(1. 哈爾濱工程大學自動化學院, 黑龍江 哈爾濱 150001;2. 中國船舶工業集團公司第708研究所, 上海 200011)

0 引 言

航母是現代海上作戰的重要組成,隨著世界各國對領海安全的重視,研究航母作戰能力成為新的熱點。航母作戰能力主要體現為艦載機的出動能力[1-3]。研究對比不同作戰方案的艦載機出動能力有利于最終作戰方案的確定[4-5]。因此,評估艦載機出動能力具有重要的理論意義和應用價值。

由于影響艦載機出動能力的因素數量多且關系復雜,因此評估的重點在于權重系數的確定。通常,對于復雜系統的評估,采用主觀的層次分析法(analytic hierarchy process, AHP),通過專家評分獲得最終的評估結果。文獻[6]提出了螢火蟲算法-層次分析算法,從全局對判斷矩陣的一致性進行檢驗,對AHP中各要素的排序權值進行全局最優求解,實現算法參數少、求解簡單、收斂速度快的目的。文獻[7]考慮在確定綜合評價指標相對權重的過程中,采用改進的可拓層次分析法與動態加權法有機結合的方法,既能夠解決同類型指標權重難以確定的問題,又能夠綜合考慮專家的個體差異及人為判斷的柔性因素對評價結果造成的主觀影響。文獻[8]提出一種新的相對基偏好表示方法,在多個等級上同時刻畫成對方案間的優于、劣于、無差異和不確定4種關系。文獻[9]整合了層次分析法和模糊綜合評價法。文獻[10]利用模糊層次分析法解決了多準則決策模型問題。文獻[11]基于歐洲質量管理基礎提出了一種結合模糊邏輯、層次分析法和業務研究方法。然而,這些評估方法主觀性和片面性較強,容易忽略較多評估指標之間的相關性和矛盾性等聯系,因此難以對多元評估對象進行全面客觀地評價。

由于艦載機出動能力指標較多,各個指標之間可能存在一定的相關性,而指標間相關將對評估對象產生重復信息。而主成分約簡法能夠從眾多相關的指標中約簡出相互獨立的指標,并且保證約簡后數據信息損失最小。文獻[12]提出基于Lp-模的稀疏主成分分析降維方法,通過極大化帶有稀疏正則項的Lp-模樣本方差,使得其在降維的同時保證了稀疏性和魯棒性。文獻[13]根據主成分分析法的降維去噪技術和核獨立成分分析法的盲源分離技術,提出了一種關于兩者的融合方法。文獻[14]提出一種基于互信息的主成分分析特征選擇算法,該算法計算特征間的互信息,以互信息矩陣的特征值作為評價準則確定主成分的個數,并衡量主成分分析特征選擇的效果。文獻[15]在粒子濾波框架下,提出了一種基于概率主成分分析表觀模型的視覺跟蹤算法。文獻[16]提出一種新的空間稀疏數據的主成分分析預測方法。文獻[17]利用主成分分析法和模糊決策樹解決分類問題。

突變級數法沒有對指標采用權重,但它考慮了各評估指標的相對重要性,從而減少了主觀性又不失科學性、合理性,而且計算簡單準確。文獻[18]將突變級數理論應用于礦場頂板安全分類中。文獻[19]將粗糙集理論與突變級數理論相結合來分析土地生態過程。文獻[20]將突變級數法和指標偏離度思想相結合提出基于突變級數法的障礙診斷模型。

本文利用主成分約簡方法結合突變級數方法(principal component reduction and sudden change progression method, PCR-CPM)對艦載機出動能力進行客觀評估,避免傳統的評估方法主觀性較強和評估過程復雜的特點,本文主要結構如下:首先,確定艦載機出動能力指標體系的層次結構;其次,利用主成分約簡方法將具有相關性的原始指標轉換成相互獨立的主分量;然后,利用突變級數方法對相互獨立的主分量進行評估計算;最后,通過與傳統的評估方法進行比較,驗證新的綜合評估方法的有效性和可靠性。

1 艦載機出動能力指標

目前,國內對于航母的使用經驗很少,作為理論研究,借鑒國外相關研究成果來指導評估指標體系的建立。利用遞歸層次法建立具有層次性、相關性和矛盾性的三級評估指標體系。圖1總結了國外常用的艦載機出動能力評估指標[1-3]。

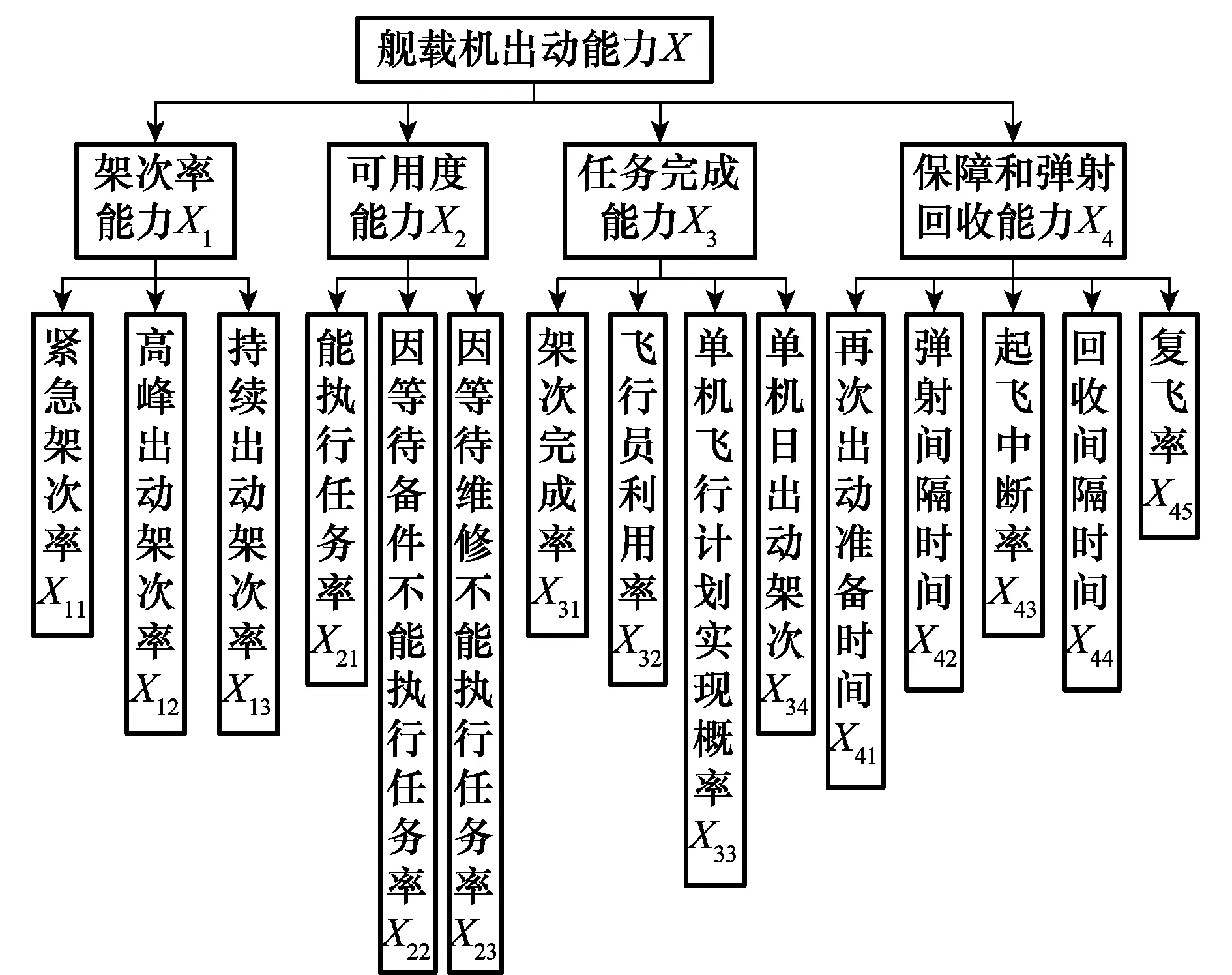
圖1 指標體系Fig.1 Index system

各個指標定義如下:

(1) 緊急架次率(單位:架次):按一定的戰備警戒等級,在幾分鐘或十幾分鐘內,已經準備好起飛的艦載機以最快速度能起飛的數量。

(2) 高峰出動架次率(單位:架次/天):航母在短時間內(4天)高強度出動時,平均一天出動的架次。

(3) 持續出動架次率(單位:架次/天):航母在持續作戰時間內(30天),平均一天能出動的架次。

(4) 能執行任務率(單位:%):在一定的飛行計劃和后勤維修供應能力條件下,艦載機至少能執行一項規定任務的時間所占的比例。

(5) 因等待備件不能執行任務率(單位:%):由于等待供給系統的備件而不能執行任務的艦載機所占的比例。

(6) 因等待維修不能執行任務率(單位:%):由于維修原因(正在維修或等待維修人員)使艦載機處于故障狀態的時間所占的比例。

(7) 架次完成率(單位:%):按計劃完成出動的架次占原計劃出動架次的比例。

(8) 飛行員利用率(單位:次/天):指飛行員平均每天的使用次數,包括:順利起飛的架次,備用架次,以及起飛中斷的架次。

(9) 單機飛行計劃實現概率(單位:%):在一定的約束條件下,在給定時間內,單架艦載機能實現飛行計劃的概率。

(10) 單機日出動架次(單位:架次/天):在一定的約束條件下,單架艦載機每天為完成特定任務而起飛、飛行和著艦的架次數。

(11) 再次出動準備時間(單位:分鐘):在一定資源配置條件下,艦載機降落后準備再次出動所需要的時間。

(12) 彈射間隔時間(單位:分鐘):單部彈射器彈射一架飛機所需的平均時間。

(13) 起飛中斷率(單位:%):起飛前因故障或其他原因終止起飛的架次占所有預飛架次的比例。

(14) 回收間隔時間(單位:分鐘):回收一架艦載機所需要的平均時間。

(15) 復飛率(單位:%):進場的艦載機未能成功著艦而復飛的次數占艦載機總進場次數的比例。

2 主成分約簡方法

2.1 主成分約簡原理

由于艦載機出動能力指標較多,各個指標之間可能存在一定的相關性,而指標間相關將對評估對象產生重復信息。利用主成分約簡法,能夠從眾多相關的指標中約簡出相互獨立的指標,并且保證約簡后數據信息損失最小。

主成分約簡通過比較各個指標的貢獻值確定指標的重要程度。

2.2 主成分約簡步驟

主成分約簡步驟如圖2所示。

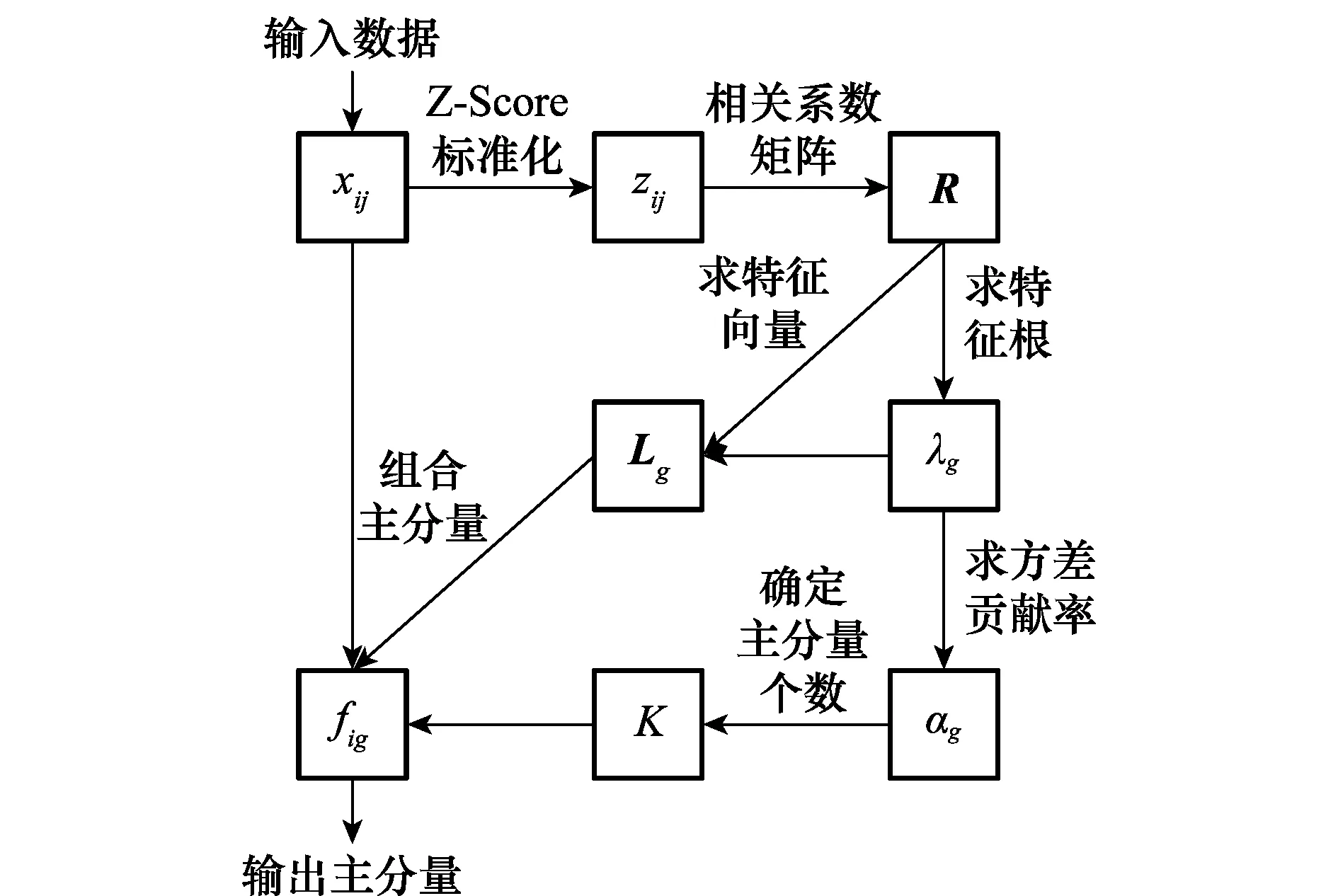
圖2 約簡過程Fig.2 Process of reduction

具體步驟如下:

步驟1指標參數標準化

由于各個指標的量綱不同,存在不可公度性問題,需要對各個指標進行無量綱化處理,通過數值變換來消除指標間的量綱影響。對于原始數據矩陣X=[xij]n×m,n為對象數量,m為指標數量,采用Z-Score法對指標進行標準化處理為Z=[zij]n×m:

(1)

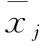
步驟2確定指標之間的相關系數矩陣R

R=[rjk]m×m,rii=1

rjk=rkj

(2)

步驟3確定R陣的特征根

R的特征方程為

|λgIm-R|=0

(3)

式中,λg(g=1,2,…,m)為特征根,表明分量的重要性。

步驟4確定R陣的特征向量

由方程組求特征向量

[λgIm-R]Lg=0

(4)

式中,L是m維實向量。

步驟5確定R陣的貢獻率

αg為貢獻率,其表達式為

(5)

步驟6確定主分量的個數K

將各個分量按照貢獻率大小排序,如果原始個數較多,則取前K個代表所有分量。

(6)

根據α(K)≥95%確定主分量個數。

最終可以將m個相關指標約簡為K個不相關的主分量fi1-fiK。

(7)

經過約簡之后的指標體系如圖3所示。

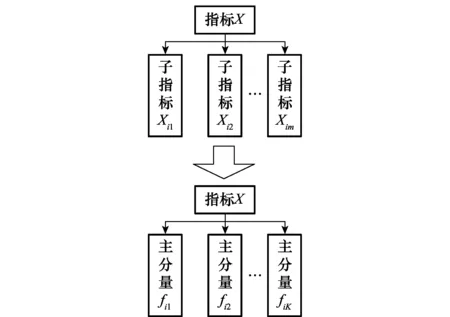
圖3 約簡后指標體系Fig.3 System after reduction

3 突變級數評估方法

3.1 突變級數評估描述

在制定艦載機作戰方案的過程中,需要從多個備選方案中快速選出最優方案。按照突變級數法,所得突變級數化為0-1的數,突變級數越大的方案較好。

3.2 突變級數評估步驟

突變級數方法步驟如圖4所示。

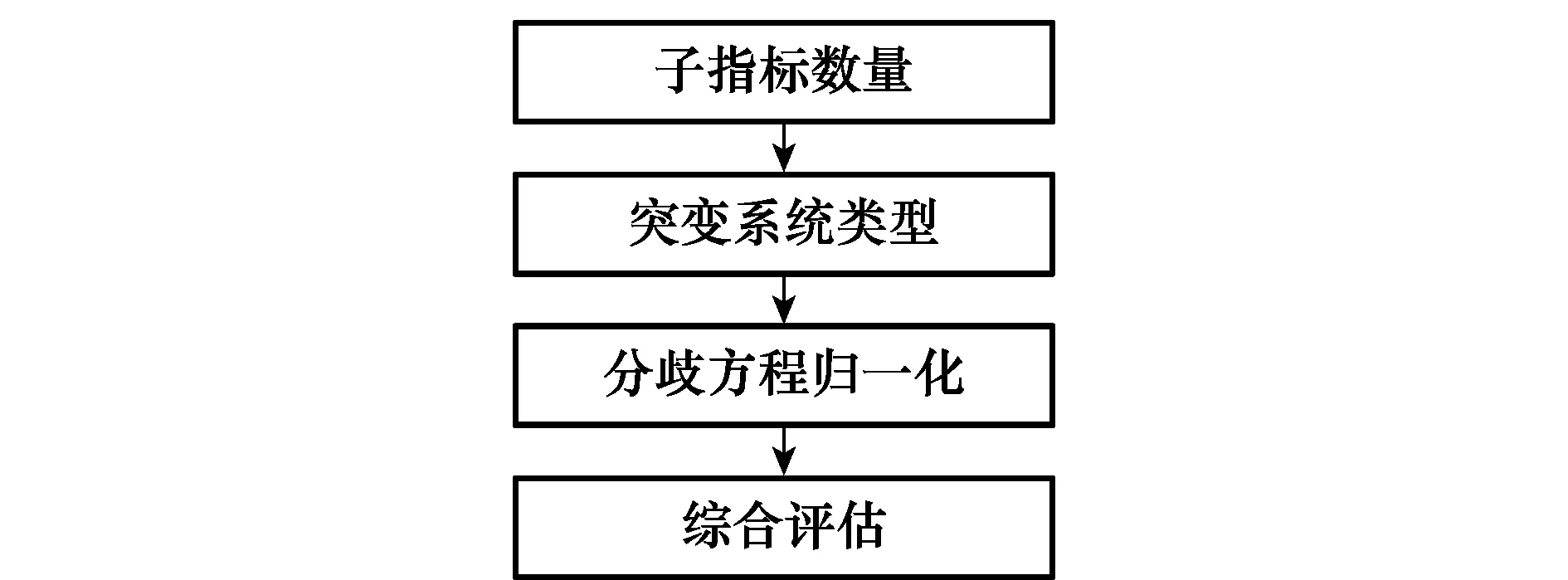
圖4 突變級數評估過程Fig.4 Evaluation process with catastrophe progression method

步驟1確定突變評估指標體系的突變系統類型

根據指標的子指標數量確定突變系統模型,如表1所示。表1中勢函數是7種初等突變類型的常見的3種,根據一個指標可以分解的子指標個數確定突變函數。如果可分解為2個子指標,系統可視為尖點突變系統。如果可分解為3個子指標,系統可視為燕尾突變系統。如果可分解為4個子指標,系統可視為蝴蝶突變系統。

表1 突變系統

表1中,f(x)為一個指標x的勢函數;a,b,c和d為子指標,重要性從高到低。

步驟2歸一公式

通過對勢函數f(x)求一階倒數得到臨界點,其表達式為

f′(x)=0

(8)

通過對勢函數f(x)求二階倒數得到奇點,其表達式為

f″(x)=0

(9)

將x消掉,求出歸一公式。

步驟2.1尖點突變系統分解形式的分歧點集方程為

a=-6x2,b=8x3

(10)

化為突變模糊隸屬函數,即如下歸一公式：

xa=a1/2,xb=b1/3

(11)

式中,xa為對應a的x值;xb為對應b的x值。

步驟2.2燕尾突變系統分解形式的分歧點集方程為

a=-6x2,b=8x3,c=-3x4

(12)

化為突變模糊隸屬函數,即如下歸一公式：

xa=a1/2,xb=b1/3,xc=c1/4

(13)

步驟2.3蝴蝶突變系統分解形式的分歧點集方程為

a=-10x2,b=20x3,c=-15x4,d=4x5

(14)

化為突變模糊隸屬函數,即如下歸一公式：

(15)

歸一公式實質上是一種多維模糊隸屬函數。

步驟3綜合評估

當存在多種方案時,取每個方案的目標為A1,A2,…,Am,則最優結果為

C=A1∩A2∩…∩Am

(16)

相應的隸屬函數為

μ(x)=μA1(x)∧μA2(x)∧…∧μAm(x)

(17)

式中,μAi(x)為Ai的隸屬函數,為最小目標值。

4 艦載機出動能力評估

4.1 艦載機出動能力評估樣本

選取“尼米茲”航母在1997年的高強度演習為評估對象[1],為保證主成分約簡的科學性,隨機抽取10個方案作為樣本,數據如表2～表5所示。

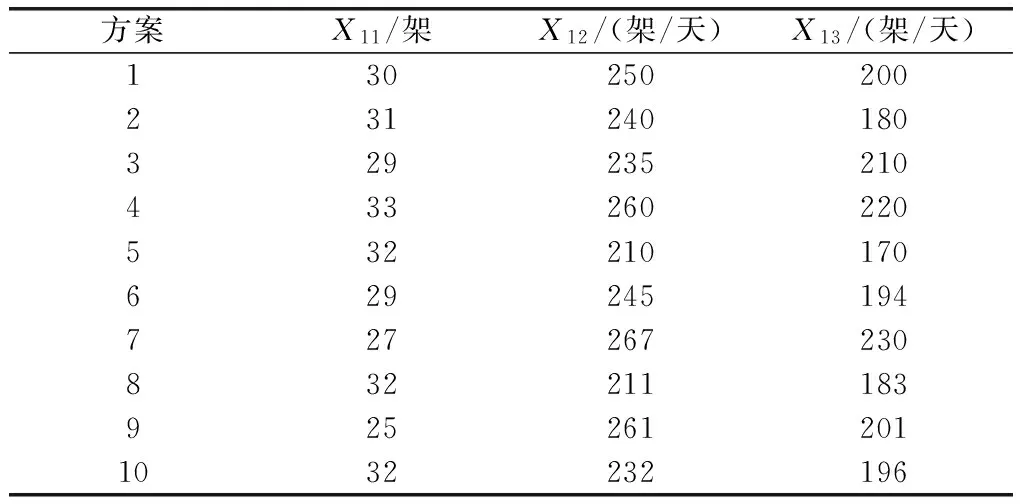
表2 架次率能力指標

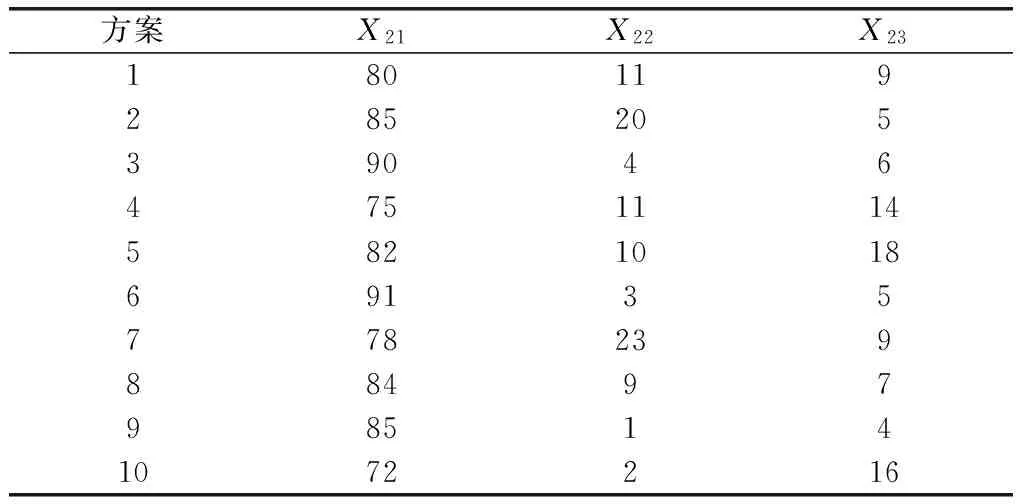
表3 艦載機可用度能力指標

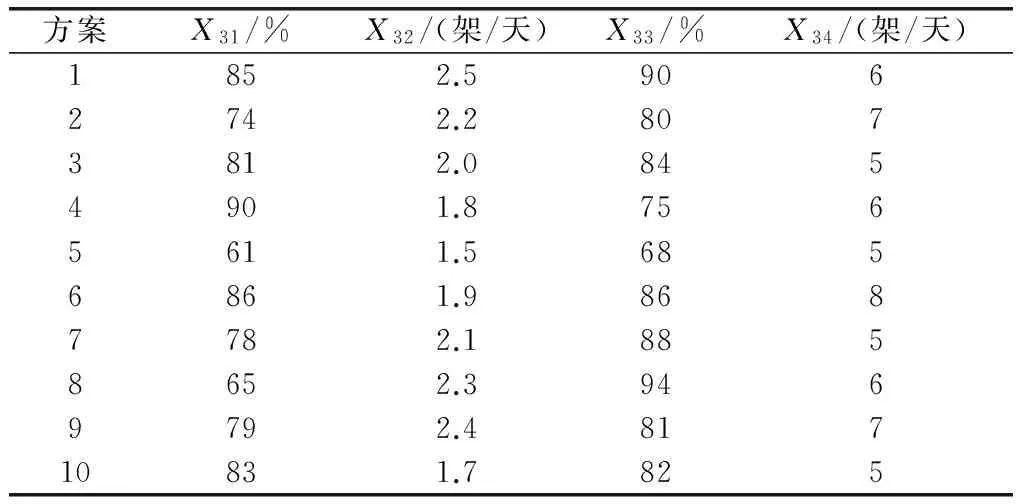
表4 任務完成能力指標

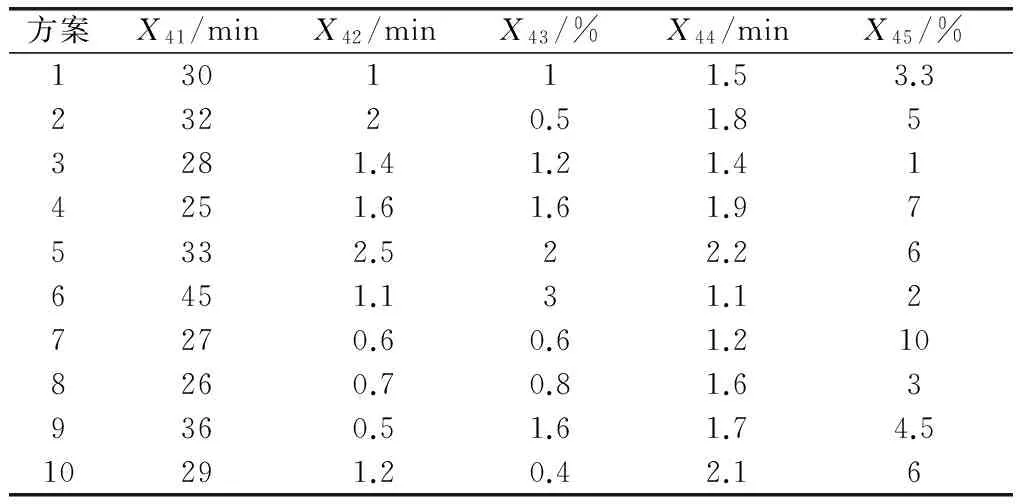
表5 保障和彈射回收能力指標

4.2 指標約簡

以保障和彈射回收能力X4指標的主成分約簡為例。

步驟1標準化

采用Z-Score法進行標準化,結果如圖5所示。

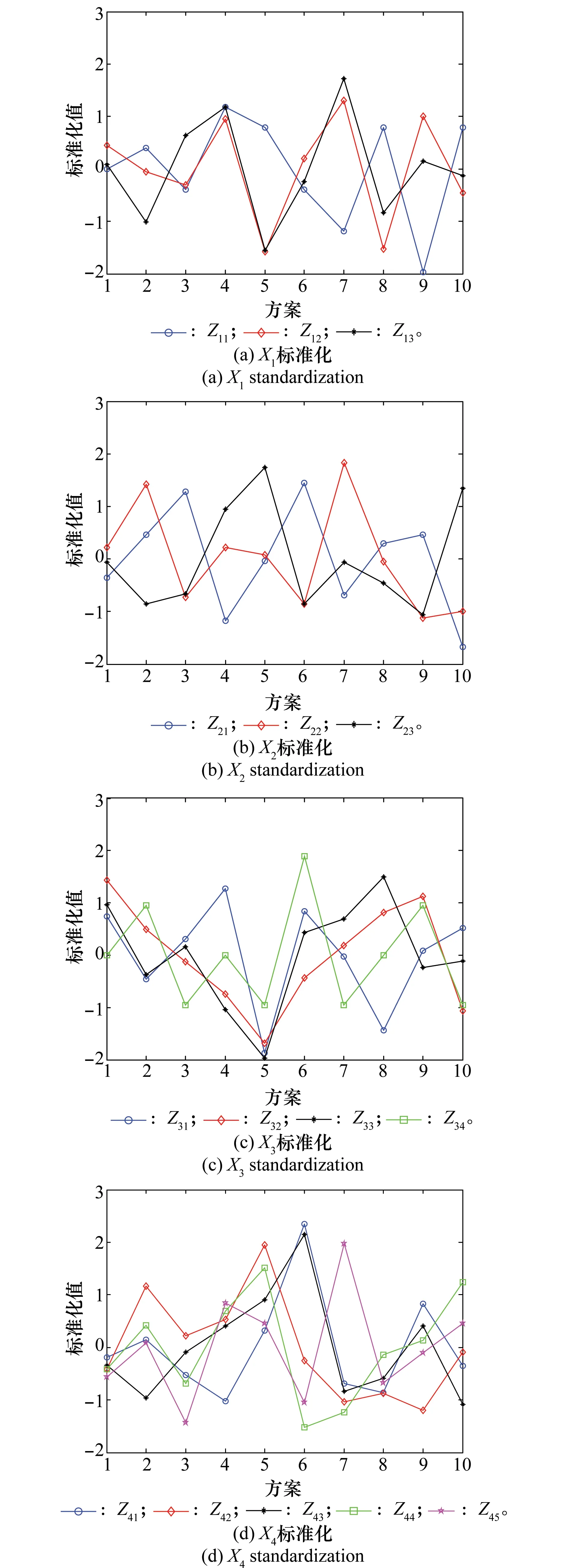
圖5 X標準化Fig.5 Standardization of X

步驟2指標數據間的相關系數矩陣

R=

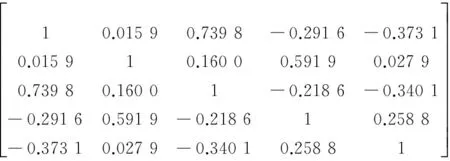
(18)

步驟3相關系數矩陣特征根

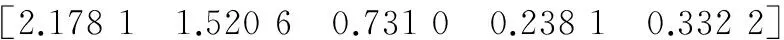
(19)

步驟4相關系數矩陣特征向量

(20)

步驟5計算貢獻率

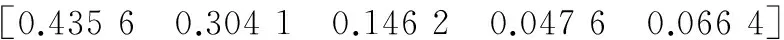
(21)

步驟6確定主分量個數

取α(K)≥95%,將α按照由大到小順序排列:

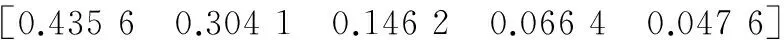
(22)

當K=4時,α(K)=95.24%≥95%。

步驟7確定約簡主分量

由特征根、特征向量和主分量個數最終確定保障和彈射回收能力X4指標的約簡主分量f41、f42、f43和f44:

(23)

同理,重復步驟1～步驟7,可以確定架次率能力X1指標、艦載機可用度能力X2指標和任務完成能力X3指標的約簡主分量:

(24)

(25)

(26)

由式(23)～式(26)和貢獻率,可得到綜合得分模型:

(27)

根據式(27)可知各個子指標的重要性,權重確定圖如圖6所示。

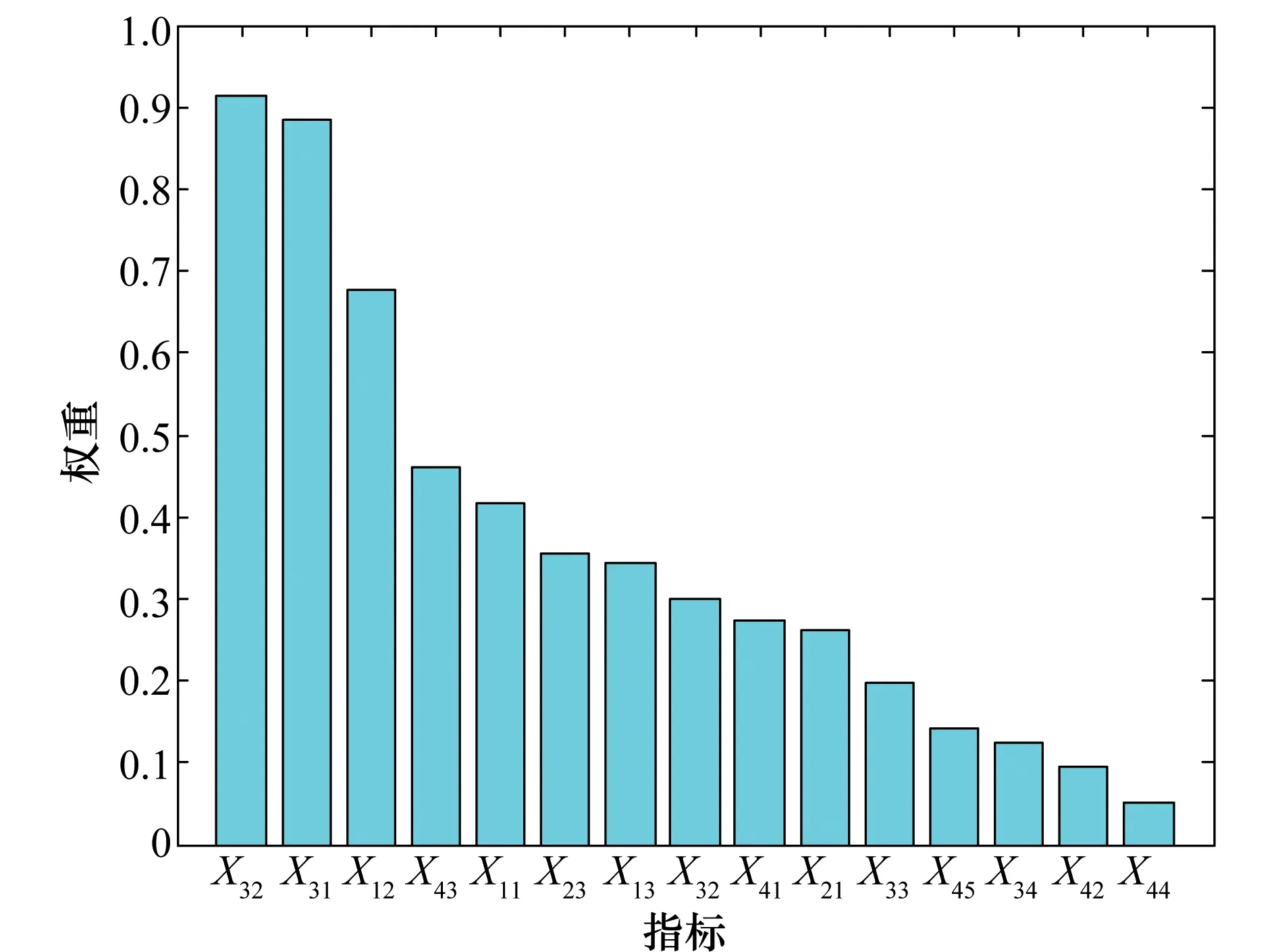
圖6 主成分分析權重Fig.6 Weights of principal components

從圖6中可以直觀了解各個子指標的重要性的高低。同時,由圖6可知,最重要的子指標為飛行員利用率和架次完成率,其指標權重遠大于其他指標的權重。

4.3 突變級數評估

約簡后的指標體系如圖7所示。

突變級數評估步驟:

步驟1計算約簡主分量評估值并歸一化

以架次率能力X1指標的主分量f11,f12和f13的歸一化為例,結果如表6所示。

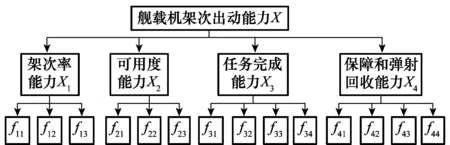
圖7 約簡后指標體系Fig.7 Reduced system

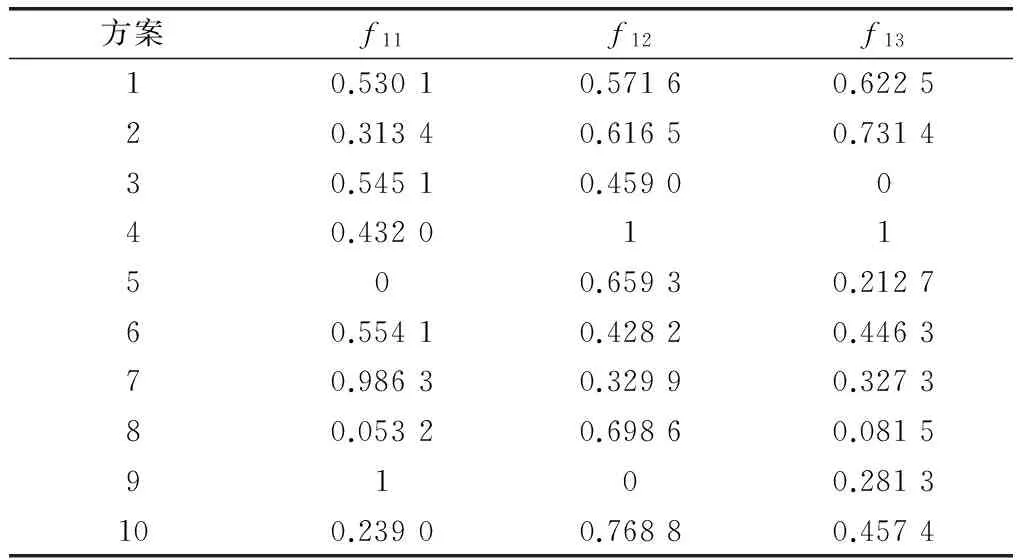
方案f11f12f1310.53010.57160.622520.31340.61650.731430.54510.4590040.432011500.65930.212760.55410.42820.446370.98630.32990.327380.05320.69860.08159100.2813100.23900.76880.4574

步驟2根據突變類型,計算評估值

計算指標X1,X2,X3和X4突變級數評估值。由于X1和X2子指標個數為3,突變類型為燕尾型。由于X3和X4子指標個數為4,突變類型為蝴蝶型。因此，計算評估值如表7所示。

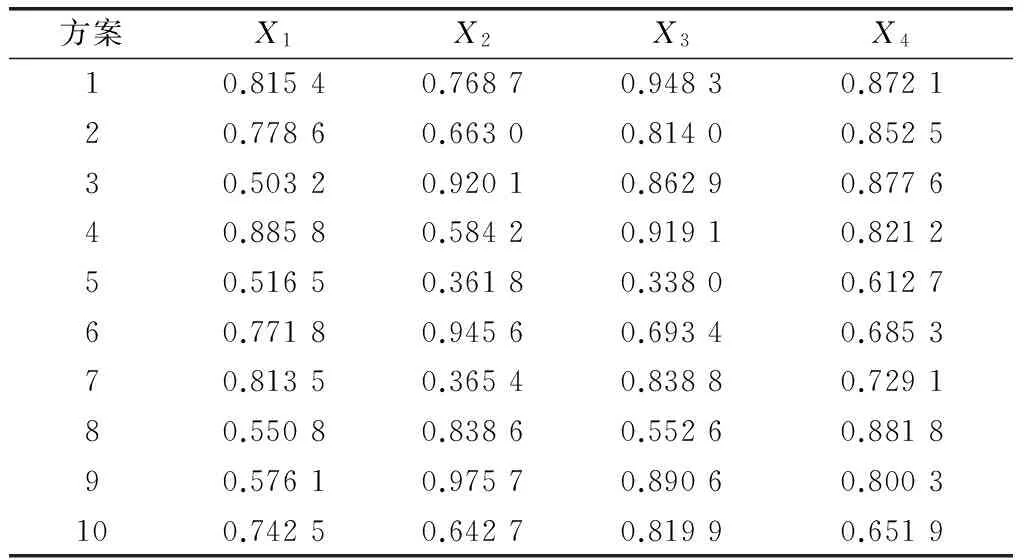
表7 指標X4突變級數評估值

步驟3計算X評估值

由于指標X子指標個數為4,突變類型為蝴蝶型,最終10個方案的評估結果如表8所示。

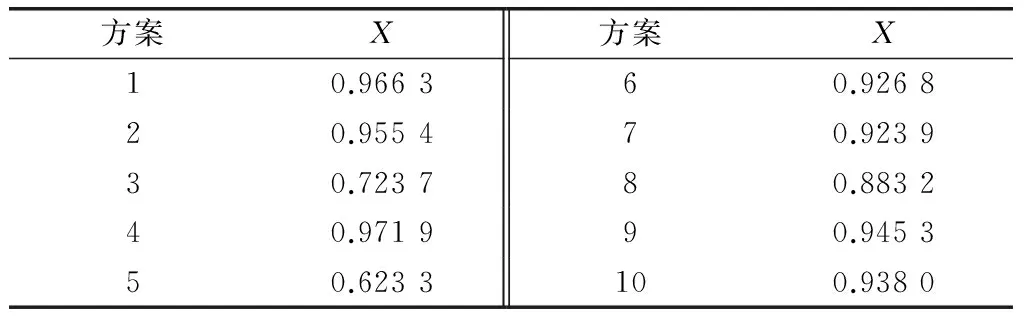
表8 指標X突變級數評估值

4.4 綜合評估結果分析

為了驗證基于主成分約簡和突變級數評估方法的有效性,將本文提出的PCR-CPM評估結果與文獻[10]的模糊AHP(fuzzy AHP, F-AHP)評估結果進行對比,如圖8所示。兩種評估結果的偏差如圖9所示。

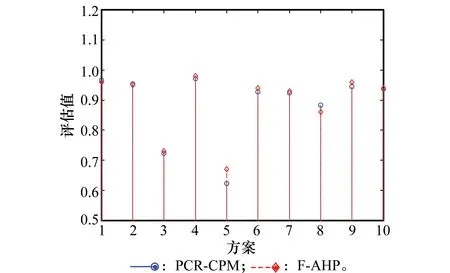
圖8 評估結果對比Fig.8 Evaluation comparison

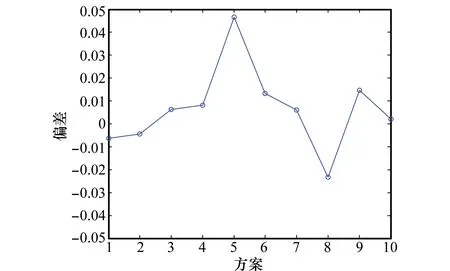
圖9 評估結果的偏差Fig.9 Evaluation deviations

由圖8和圖9可知,基于主成分約簡和突變級數評估結果與AHP評估結果基本一致,說明基于主成分約簡和突變級數評估方法是有效可靠的,同時避免了AHP評估方法的依靠專家的主觀賦權問題,能夠較為客觀地評估方案的優劣。

對于方案5的評估,AHP的評估結果為0.667 8,本文所提方法的評估結果為0.623 3,AHP的評估結果較高,而方案5中持續出動架次率為170架/天,與其他方案相比最低,因等待維修不能執行任務率為18%,與其他方案相比最高,剩余指標與其他方案相近,通過分析可知持續出動架次率和因等待維修不能執行任務率是較為重要的兩個指標,因此這個方案的評估值應與其他方案的評估值差距較大,AHP的評估結果顯示其與方案3的結果接近,這是由于主觀賦權時只體現了指標之間哪個更為重要,但是指標之間的差距大小受主觀影響可能存在與實際結果不符的情況。而本文所提方法避免了主觀影響對結果造成的影響,更為客觀可信。

因此,所選的10個方案的優劣可以根據綜合評估值確定,結果如圖10所示。

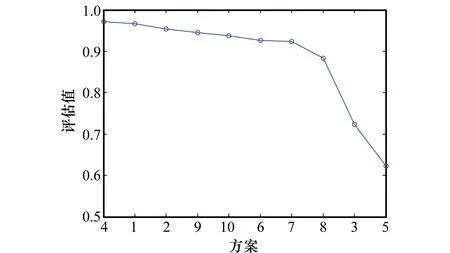
圖10 方案優劣排序Fig.10 Scenarios order

由圖10可知,10個方案中最好的方案為方案4,綜合評估值為0.971 9,最差的方案為方案5,綜合評估值為0.623 3。

因此,基于主成分約簡和突變級數綜合評估方法實現了對艦載機出動能力的指標重要性分析和方案排序,保證了評估的客觀性、可靠性和快速性。

5 結 論

本文給出了基于主成分約簡和突變級數的艦載機綜合評估方法,得到以下結論:

(1) 在確定艦載機出動能力指標體系的基礎上,針對指標之間的高度相關性的特點,采用主成分約簡方法,將相關的指標轉換成相互獨立分量,消除了評估指標之間的相關關系的影響,并根據貢獻度確定主分量。

(2) 利用突變級數法對約簡后的主分量進行評估,方法簡易,不用權重,大大減少了評估的主觀性,同時,突變級數法實際上是一種多維模糊隸屬函數,適合于矛盾的多目標評估決策問題,解決了傳統的評估方法對矛盾的目標難以處理的問題。

(3) 利用主成分約簡和突變級數法相結合的方法,實現對艦載機出動能力的兩級綜合評估。實現了對艦載機出動能力的指標重要性分析和方案排序,保證了評估的客觀性、可靠性和快速性。當已知每個指標的實際取值范圍時,可以利用本文所提方法在該范圍內獲得最優方案。

基于主成分約簡和突變級數的評估方法可用于其他具有強相關性或矛盾性的復雜系統的評估,簡化評估過程。

[1] ANGELYN J, MAUREEN A W, COLLEEN M K G, et al. USS nimitz and carrier airwing nine surge demonstration[D]. Alexandria: Center for Naval Analyses, 1998.

[2] JEWELL A. Sortie generation capacity of embarked airwings[D]. Alexandria: Center for Naval Analyses, 1997.

[3] PATTEN M P. Forecasting carrier air-wing operational availability with event step simulation[D]. Monterey: Master thesis of Naval Postgraduate School, 1999.

[4] XIA G Q, LUAN T T, SUN M X. Evaluation analysis for sortie generation of carrier aircrafts based on nonlinear fuzzy matter-element method[J]. Journal of Intelligent and Fuzzy Systems, 2016, 31(6): 3055-3066.

[5] XIA G Q, LUAN T T, SUN M X, et al. Research on modeling of parallel closed-loop support process for carrier aircraft based on system dynamics[J]. International Journal of Control and Automation, 2016, 9(11): 259-270.

[6] 范陽濤,汪民樂,文苗苗,等.基于螢火蟲算法-層次分析法的彈道導彈突防效能分析[J].系統工程與電子技術,2015,37(4): 845-850.

FAN Y T, WANG M L, WEN M M, et al. Analysis of ballistic missile penetration effectiveness based on FA-AHP[J]. Systems Engineering and Electronics, 2015, 37(4): 845-850.

[7] 高煒, 張慶普, 敦曉彪, 等. 基于改進的可拓層次分析法和動態加權的航天高技術綜合評價研究[J]. 系統工程與電子技術, 2016, 38(1): 102-109.

GAO W, ZHANG Q P, GUO X B, et al. Comprehensive assessment of advanced military aerospace technologies based on improved EAHP and dynamic weighting[J]. Systems Engineering and Electronics, 2016, 38(1): 102-109.

[8] 付超, 侯震. 基于多等級方案成對比較的決策方法[J]. 控制與決策, 2015, 30(10): 1828-1834.

FU C, HOU Z. Decision method based on pairwise comparison of alternatives on multiple grades[J]. Control and Decision, 2015, 30(10): 1828-1834.

[9] NGUYEN H T, DAWAL S Z M, NUKMAN Y, et al. An integrated approach of fuzzy linguistic preference based AHP and fuzzy COPRAS for machine tool evaluation[J]. Plos One, 2015, 9: 1-24.

[10] SALIMI N, REZAEI J. Multi-criteria university selection: formulation and implementation using a fuzzy AHP[J]. Journal of Systems Science & Systems Engineering, 2015, 24(3): 1-23.

[11] EZZABADI J H, SARYAZDI M D, MOSTAFAEIPOUR A. Implementing fuzzy logic and AHP into the EFQM model for performance improvement: a case study[J]. Applied Soft Computing, 2015, 36(C): 165-176.

[12] 李春娜, 陳偉杰, 邵元海. 魯棒的稀疏Lp-模主成分分析[J]. 自動化學報, 2017, 43(1): 142-151.

LI C N, CHEN W J, SHAO Y H. Robust spare Lp-norm principle component analysis[J]. Acta Automatica Sinica, 2017, 43(1): 142-151.

[13] 梁勝杰, 張志華, 崔立林, 等. 基于主成分分析與核獨立成分分析的降維方法[J]. 系統工程與電子技術, 2011, 33(9): 2144-2148.

LIANG S J, ZHANG Z J, CUI L L, et al. Dimensionality reduction method based on PCA and KICA[J]. Systems Engineering and Electronics, 2011, 33(9): 2144-2148.

[14] 范雪莉, 馮海泓, 原猛. 基于互信息的主成分分析特征選擇算法[J]. 控制與決策, 2013, 28(6): 915-919.

FAN X L, FENG H H, YUAN M. PCA based on mutual information for feature selection[J]. Control and Decision, 2013, 28(6): 915-919.

[15] 張輝, 趙保軍. 基于概率主成分分析表觀模型的視覺跟蹤[J]. 系統工程與電子技術, 2009, 31(12): 2826-2829.

ZHANG H, ZHAO B J. Visual tracking based on probabilistic PCA appearance model[J]. Systems Engineering and Electronics, 2009, 31(12): 2826-2829.

[16] JANDAROV R A, SHEPPARD L A, SAMPSON P D, et al. A novel principal component analysis for spatially misaligned multivariate air pollution data[J].Journal of the Royal Statistical Society,2016, 66(1): 3-28.

[17] VARMA K V S R P, RAO A A, MAHALAKSHMI T S, et al. A computational intelligence technique for the effective diagnosis of diabetic patients using principle component analysis(PCA) and modified fuzzy SLIQ decision tree approach[J]. Applied Soft Computing, 2016, 49: 137-145.

[18] CHEN H J, LI X B, LIU A H. Classification of stope roof safety based on catastrophe progression method and its application[C]∥Proc.of the 7th International Symposium on Rockburst and Seismicity in Mines, 2009: 195-202.

[19] CAO W, ZHOU S L, WU S H. Land-use regionalization based on landscape pattern indices using rough set theory and catastrophe progression method[J]. Environmental Earth Sciences, 2015, 73(4): 1611-1620.

[20] 陳曉紅,楊立.基于突變級數法的障礙診斷模型及其在中小企業中的應用[J].系統工程與電子技術,2013,33(6):1479-1485.

CHEN X H, YANG L. Obstacle diagnosis model based on the catastrophe progression method and its applications for the small and medium-sized enterprises[J]. Systems Engineering and Electronics, 2013, 33(6): 1479-1485.