基于相關矩陣與概率模型的故障模糊診斷

張 弢, 王金波, 張 濤

(1. 中國科學院大學, 北京 100049;2. 中國科學院空間應用工程與技術中心, 北京 100094)

0 引 言

隨著航空航天、機械、信息等領域的快速發展,復雜工作環境對系統裝備的快速反應需求日益提高,系統級故障快速診斷、以及信息獲取不充分或不確定條件下的故障模糊診斷正成為研究的熱點[1-10]。圍繞故障診斷問題,國內外學者已基于信息流、多信號等系統可測性模型開展了大量卓有成效的研究[11-13];文獻[14-15]基于節約覆蓋集理論推理出故障最大似然概率診斷模型;文獻[16-19]提出基于機器學習及證據理論的故障診斷改進方法;文獻[20-22]提出基于圖論方法的診斷改進模型;文獻[23-24]提出基于貝葉斯網絡的混合診斷方法。上述研究成果已成功應用于航空航天、高壓輸變電、電子信息、機械控制等工程領域。

對于復雜系統而言,故障與其征兆之間通常存在不確定性,此時診斷問題將超出理想假設下故障推理方法的適用范圍,并且故障源發概率通常難于獲取,傳統基于貝葉斯理論的故障診斷方法也將面臨失效。針對此問題,基于有向圖模型的模糊故障診斷算法[3]提供了新的解決思路,該算法將故障發生的判定依據選取為測試向量與故障特性向量的空間向量夾角大小,并已在航天工程領域驗證了算法的有效性。但該算法未從故障特征模糊性角度深入剖析模糊診斷機理,未能利用概率空間中的標量運算特性降低算法復雜度,未考慮利用最小模原則篩選故障診斷結果以降低虛警,在載人航天、載人深潛等快速反應需求較高的應用場景中存在明顯局限性。

本文基于故障測試傳感器的測試不確定性分析提出了一種故障模糊診斷方法,通過建立故障-測試相關矩陣,在故障特征空間中考察非理想測試條件下故障出現某種征兆的概率值,并利用概率最值原則推理故障、以及最小模原則進行故障篩選以降低虛警,實現了對復雜系統故障的高效便捷診斷。對實驗結果分析易知,本文所用方法的首選結論診斷正確率及故障覆蓋率均可達到100%,相比文獻[3],本文方法的運算復雜度更低、并且支持現場應急條件下人工圖形化快速診斷。

1 相關矩陣

相關矩陣是一種表述兩組對象序列間多重因果關系的有效方法。在系統測試性分析和故障診斷工作中,通常采用基于信息流、多信號流圖等方式進行可測性設計,繼而可建立故障-測試相關矩陣以支持故障的定位與隔離。相關矩陣的基本概念[25]簡要介紹如下。

定義1相關關系:是指兩個對象之間的因果關系。由對象a可直接推知對象b,則稱a與b是1階相關。若由對象a推知對象b,再由對象b推知對象c,則b與a、c與b分別為1階相關,c與a為2階相關。兩個對象間的N階相關關系,可同理推知。

定義2相關性矩陣:反映各對象間各階相關關系(也稱全階相關關系)的布爾矩陣。矩陣的行向量和列向量均由對象組成,若某行對象與某列對象相關,則矩陣相應行列位置的元素取值為1,否則取值為0。

在故障診斷領域,常用如式(1)所示的矩陣DFT表達故障-測試相關關系,其中以標記f表示故障對象、標記t表示測試對象、標記r表示故障與測試對象間的相關關系。當故障fi可被測試tj檢測到,則矩陣對應位置元素rij=1,否則rij=0。矩陣的行向量Fi=[ri1,ri2,…,rin]代表了故障的征兆向量(又稱特征向量),其定義了故障fi發生時對應的全部測試的外在表達。矩陣的列向量Tj=[r1j,r2j,…,rmj]T描述了測試tj可檢出的全部故障,體現了其可檢測的最大故障包絡。

t1t2…tn

(1)

在工程實踐中,通常可對復雜系統進行測試性建模,建立故障-測試相關矩陣,進而獲得故障對象與測試對象之間完整的相關關系。下面以文獻[13]中的某型飛機燃油系統為例,簡要說明以多信號流圖為基礎的DFT矩陣建立方法。

圖1為某型飛機燃油系統的多信號流圖,其實質為基于系統結構的分層有向信息流圖。因系統級故障可分解為各部件的故障集合,故圖中的“矩形”符號也兼具表征了各部件、以及系統級可能發生的故障。通過前期可測性分析知,系統電源可能有“過壓”和“欠壓”兩種故障狀態,且均可由置于電機上的電壓傳感器間接獲知,其故障征兆分別對應測試信號T3和T4;電機及其測試級聯的電流傳感器、電壓傳感器的故障可分別由測試信號T1、T5反映;燃油泵故障及電源過壓情況,由測試信號T2予以監測。限于篇幅關系,本文僅對上述部件(故障)1～5和測試1～5的關聯關系簡要說明,并給出如表1所示的故障-測試相關矩陣,系統中其余部件及測試的相關矩陣同理可得。多信號流圖原理及用法可參見相關文獻,本文不做展開論述。

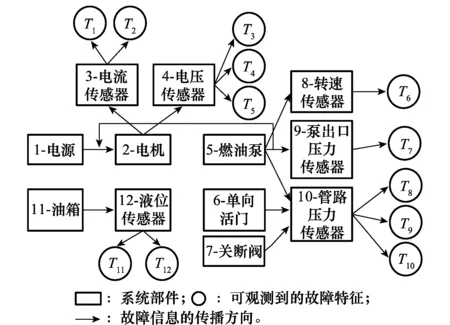
圖1 某型飛機燃油系統多信號流圖示例Fig.1 Multi-signal flow graph of an aircraft fuel system

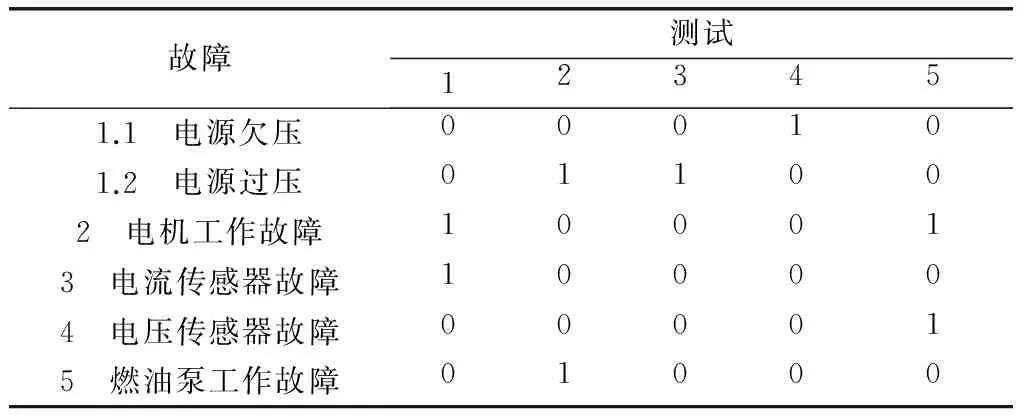
故障測試123451.1 電源欠壓000101.2 電源過壓011002 電機工作故障100013 電流傳感器故障100004 電壓傳感器故障000015 燃油泵工作故障01000

在已知故障范圍內,若不考慮故障特征發生消減及變異,則DFT矩陣中各故障特征向量(行向量)的“邏輯或”運算可用于表示系統中多故障并發的情況。對于上述多故障情況,可將待考察多故障(故障組合)的邏輯運算結果作為新的行向量添加至DFT矩陣的最下端,并將該新矩陣定義為“DFT擴展矩陣”。DFT擴展矩陣與DFT矩陣(規模m×n維)性質相同,其列向量數目為n、行向量數目最大可為2m-1。

2 基于概率模型的故障模糊診斷

2.1 故障判據選取

系統故障診斷的實質是根據已觀測到的征兆推理定位故障。在實際工作中,受限于觀測方法、設備特性、運行環境等多方面影響,觀測到的故障征兆也將存在不確定性,通常需要引入概率方法來進行故障診斷。在概率空間中,系統故障診斷問題可定義為一組條件概率的最值關聯問題,即

定理1對于給定的故障-測試條件概率集合

Pr(Cj)={p(F1|Cj),p(F2|Cj),…,p(Fm|Cj)},

j=1,2,…,n

(2)

若存在關聯函數E,使得對任意Cj均有max(Pr(Cj))=E(Fi)成立,則可診斷為故障Fi發生。式(2)中，Fi表示系統故障,Cj表示故障征兆測試向量。關聯函數E通常應具有正相關特性,并且滿足節約原則,例如最小模原則,可用于對診斷結果按需篩選。

為便于表述,本文給出故障模糊檢出率定義。

定義3故障模糊檢出率γij=p(Cj|Fi)/p(Cj)。

利用條件概率公式展開,并將定義3中的γij算式代入,則式(2)中故障后驗概率可變為

p(Fi|Cj)=p(Fi)×γij

(3)

易知式(3)的取值區間為(0,γij),故式(3)的含義為:在非理想測試條件下,故障被檢出的上限概率為γij。

對于復雜系統而言,在故障先驗概率p(Fi)難于獲取并且測試非理想情況下,γij可用于衡量測試Cj對故障Fi的最大檢出程度,與p(Fi|Cj)相比,γij是故障Fi被檢出的樂觀估計。在工程應用中,測試人員通常會計算兩個故障的γij相對值(例如“比值”或“差值”)進而找出γij最大值,以此獲得診斷結果。上述計算過程可消減γij部分估計誤差,因此以γij作為故障模糊診斷的衡量標準具有合理性。特別地,對于已觀測到的故障征兆,因其為確定事件,所以γij存在等效值為p(Cj|Fi)。

綜上所述,非理想測試條件下γij值(或等效值p(Cj|Fi))可作為故障模糊診斷的判據,將γij代入定理1可得到故障判別式：

max(γij)=max(p(Cj|Fi))=E(Fi),j=1,2,…,n

(4)

分析易知,僅需將函數E取為故障與其模糊檢出率最大值的直接關聯,式(4)即可用于模糊診斷。

2.2 模糊診斷方法

系統故障征兆觀測的不確定性直接導致了故障診斷結論的模糊性,對于既定的系統征兆和待考察故障而言,上述模糊性將表現為故障-測試依賴關系的多映射特性,即:在觀測存在不確定性條件下,系統DFT矩陣中的行向量將表現為多重故障的特征屬性,而不是某故障獨有的特征表現。為便于表述,現對比DFT矩陣的故障特征向量Fi,定義其在概率空間中的模糊特征向量如下:

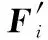
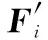
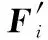
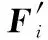
步驟1建立DFT矩陣(m×n維),并獲得系統故障檢測概率(fault detection rate,FDR)、虛警概率(false alarm rate,FAR)等統計數據;

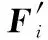
步驟3對于給定的故障征兆Cj,將其與Sp中每個元素故障的模糊特征向量進行比對,若完全相同,則按步驟4進行診斷結果篩選;否則,增大考察故障數量i并擴大集合Sp的范圍并重新執行步驟2,直至i=2m-1且Sp=Sa;

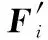
步驟5診斷結束,輸出結果。

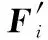
下面對故障模糊診斷方法的應用做示例說明。

案例1已知某系統需考察的故障有2個且僅有2個故障觀測點,其故障-測試相關矩陣如表2所示。故障發生概率及觀測點工作狀態概率均相互獨立。

表2 案例1的DFT矩陣

經前期數據統計,測試點1和測試點2對故障1的FDR分別為0.957 5和0.991 2,FAR分別為0.003 8和0.002 5;相應地,對故障2的故障檢測概率分別為0.963 7和0.974 2,虛警率分別為0.315 6和0.238 8。因此,對故障1和故障2的診斷辨識過程如下:

(1) 待考察故障數i=2,對應的待考察故障集合Sp={F1,F2};

(2) 集合Sp中元素故障的模糊特征向量及其出現概率如表3所示;

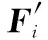
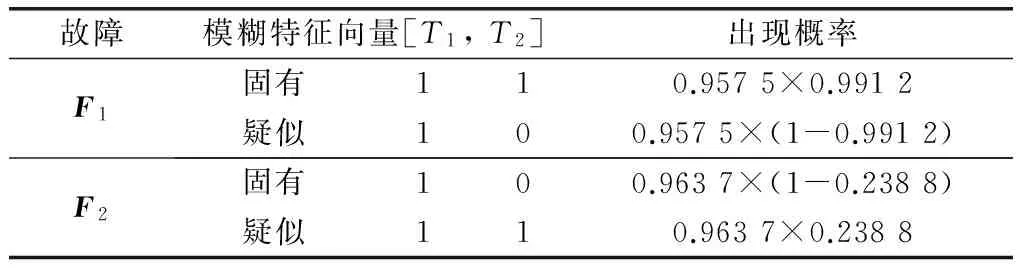
表3 案例1中各故障的模糊特征向量及概率值

(4) 輸出全部Nop=2個候選診斷結果:最可能為F1故障,次可能為F2故障。

對案例1而言,未列出的故障模糊特征向量{0,1}對應系統中未定義故障(或非故障情況),因不具備診斷條件,故不做考察。一般來說,系統的FDR應大于50%且FAR小于50%,否則與工程實際不符(工程實際中FDR通常“遠大于”FAR)。在上述條件下,容易證明,若獲得的故障征兆Cj可與某故障Fi的固有特征向量相同,則故障Fi可作為優先候選診斷結論,診斷結果具體排序依據節約原則確定。基于高階DFT矩陣的復雜系統故障診斷與案例1類似。

2.3 快速診斷模式

對于“快速粗診斷”等現場應急診斷場景,可在本文故障模糊診斷方法基礎上,進一步合理假定所有故障-測試的故障檢測率取值同為FDRarg、故障虛警率取值同為FARarg。本文將以此假設為前提的簡化診斷方法定義為“快速診斷模式”。

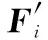
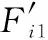
(5)

因系數ω可利用故障虛警率為來定義故障漏檢率的等效值,相對于理想測試條件而言,可實現測試結果“偏離”理想條件下系統故障的量化比較,故本文定義其為“征兆偏離系數”,工程實用中可對其進行“取整”運算以簡化分析。

基于本文故障模糊診斷方法,在參數統一量化條件下可得到故障快速診斷模式,其主要操作過程可簡記為“建矩陣、標區域、換零值、做加法”。

案例2假定某系統的DFT矩陣如表4所示,測試與故障間的FDR最大值為0.95、FAR最大值為0.01,故障發生概率及測點工作狀態概率均相互獨立,在模擬注入F2故障且獲得故障征兆Cj=[0,1,1,0]條件下,可有如下快速診斷過程。

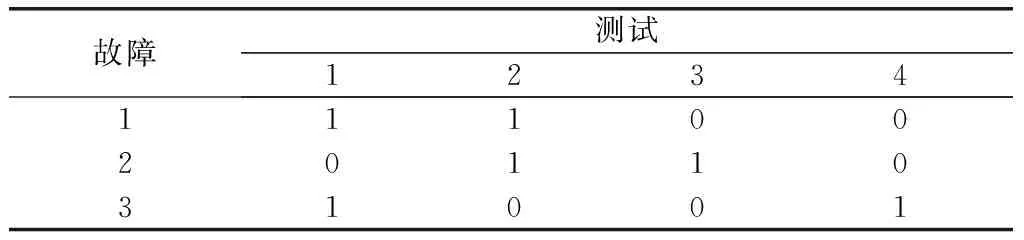
表4 案例2的DFT矩陣

(1) 預備:計算征兆偏離系數并取整有ω=5;

(2) 建矩陣:假設選定需考察故障個數為4,對應的故障集合Sp=Sa={F1,F2,F3,(F1,F2)},則考慮組合故障的DFT擴展矩陣如表5所示;

(3) 標區域+換零值:根據Cj中取值為1的列對表5標定區域(如表6中陰影部分所示),將標定區域中所有數值“0”替換為“5”(即ω值);

(4) 做加法:計算表6的DFT擴展矩陣中各行向量元素的數值累加和分別為{7,2,12,3};

(5) 診斷:依據故障模糊征兆概率“偏離”理想條件的程度越小,故障發生概率越高原則,得到的診斷結果為:最可能F2故障,次可能F1和F2組合故障,第三可能F1故障,第四可能F3故障。

由以上診斷過程可看出,快速診斷模式支持簡潔的圖形化操作,運算效率更高。

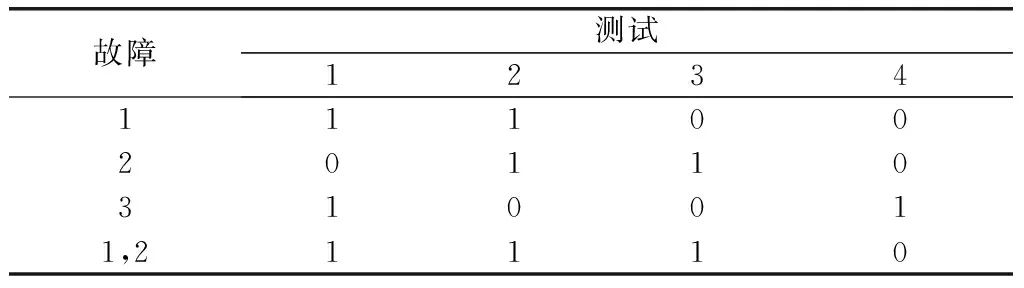
表5 案例2的DFT擴展矩陣

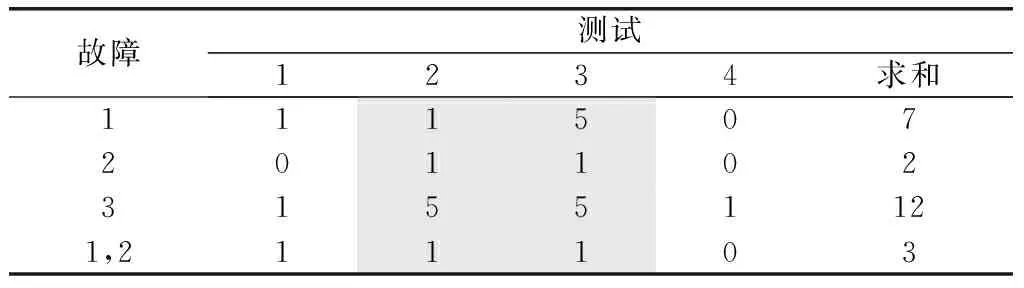
表6 案例2的DFT擴展矩陣數值替換及求和

3 應用實例及評估

本文選取阿波羅飛船發射前的系統狀態為例,證明所提出診斷方法的有效性和實用性,實驗對象數據源自文獻[26]。阿波羅飛船系統中包含了10個故障狀態及15個故障觀測傳感器,其故障-測試相關矩陣DFT如表7所示,其中字符Y表示測試發現故障征兆,字符N表示測試未發現故障征兆。

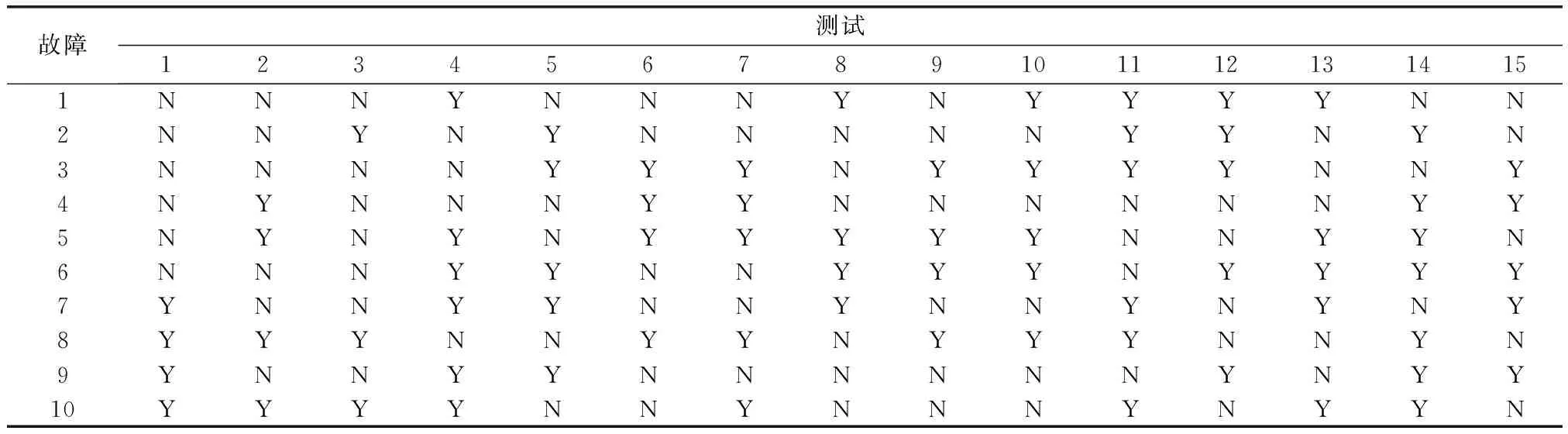
表7 飛船發射前系統狀態故障-測試相關矩陣

為方便比對故障診斷性能,本文采用了與文獻[3]相同的實驗假設條件:

(1) 系統傳感器的FDR值均為90%,FAR值均為1%,且各值相互獨立;

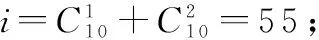
(3) 備選診斷結論中包含的最大疑似故障數Nop=3。

將診斷算法運行在CPU主頻1.83 GHz,內存1.5 G的PC機上。

實驗結果表明,在單故障及雙故障仿真注入情況下,本文基于故障模糊檢出率計算的診斷方法的“首選診斷結論的正確率”和“故障覆蓋率”均達到100%,與文獻[3]方法結論一致。容易證明,在相同實驗條件下,本文提出的快速診斷模式也可獲得相同的診斷結論。

表8給出了本文基于故障模糊檢出率計算的診斷方法與文獻[3]方法的主要實驗數據對比,因兩種方法所用的衡量指標(“相似度”與“故障模糊檢出率”)不同,故表中兩列“判據值”之間并無量值比較意義。

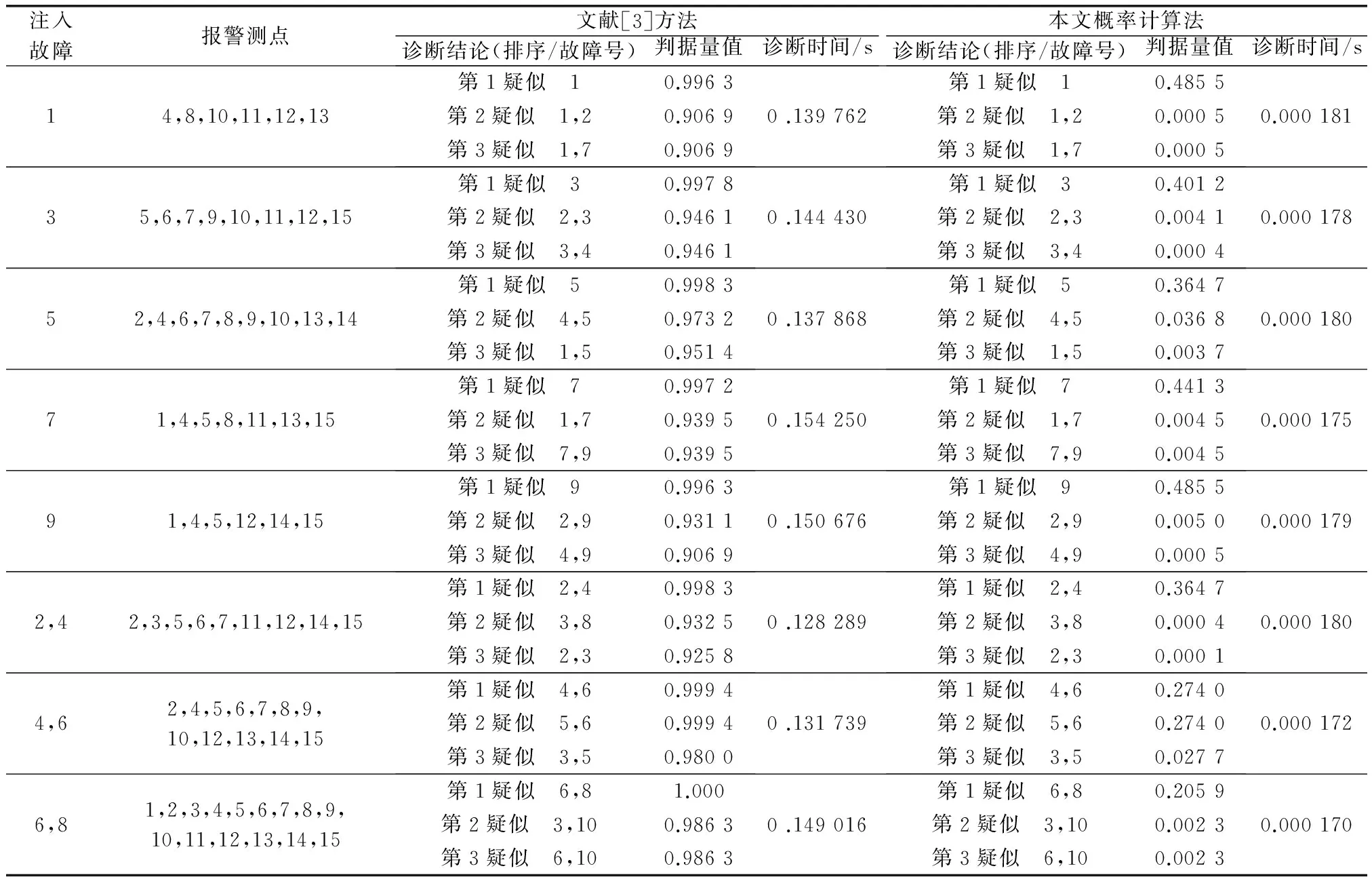
表8 理想情況下故障注入的診斷結果比較

續表8

值得說明的是,考慮到“帕列托定律”對于工程系統的故障診斷問題有一定的適用性(系統80%的故障常出現在20%的部件上),對于空間站、大型客機等復雜系統而言,在故障組合的數目巨大、多故障或故障組合具有相同模糊檢出率的條件下,本文按“最小模”原則篩選出的故障疑似范圍更小,將比文獻[3]中按任意次序確定診斷結果的方式獲得更低的FAR。

在診斷時間方面,本文提出的兩種方法均優于文獻[3]方法。表9給出了文獻[3]方法、本文提出的基于故障模糊檢出率的概率計算方法、以及本文提出的快速診斷模式等3種方法的運算復雜度對比。其中,數值m和n分別表示DFT矩陣的行數和列數,故障考察范圍為所有故障的可能組合(即共需考察2m-1行故障特征向量),同時假定各測試FDR、FAR分別相等,運算復雜度計算時忽略了取值“高階無窮小”部分。

由表9可以看出,本文提出的兩種方法的計算復雜程度均低于文獻[3]方法。這是因為文獻[3]方法未考慮概率空間中的標量運算特性。文獻[3]方法將故障特征向量和觀測向量均映射至矢量空間、并計算兩向量間夾角的大小,這隱含了觀測向量中各元素(測試)間相互獨立的前提,若在概率空間中考慮上述處理過程,并附加相同的測試獨立性前提、以及故障-測試間4種可能的條件概率信息,則上述矢量夾角運算可對應為本文觀測向量中所有元素(測試)的條件概率乘積,但將矢量運算轉換為標量運算使得本文方法的診斷效率更高。

表9 算法運算復雜度比較

特別地,本文提出的快速診斷模式中不含乘法及開平方操作(僅有加法運算),特別適用于對系統故障的快速粗略估計、或者脫離自動化診斷系統輔助狀態下的人工故障分析,可為載人航天、載人深潛等快速反應需求較高的應用場景提供故障診斷新方法。

4 結 論

本文針對航空航天等急需快速反應的應用場景引入了一種新的系統故障診斷方法。通過建立故障-測試相關矩陣,從概率角度推理出非理想測試條件下的故障判據,并利用最小模原則優選故障以降低虛警,實現了對復雜系統故障的高效便捷診斷,避免了獲取復雜系統源發故障概率或建立精確數學模型的難題。與文獻[3]相比,本文方法可在保持100%的首選結論診斷正確率及故障覆蓋率的同時,具有更低的運算復雜度,并且具備圖形化快速診斷模式,便于操作人員現場應急使用。

[1] SUN Y, GUO L, MA Z S. A fault diagnosis system design for space application[C]∥Proc.of the IEEE International Conference on Electronic Measurement & Instruments, 2015: 8-12.

[2] YAO J Y, LI J, LI H Z, et al. Modeling system based on fuzzy dynamic Bayesian network for fault diagnosis and reliability prediction[C]∥Proc.of the Reliability and Maintainability Symposium, 2015: 1-6.

[3] 連可, 黃建國, 龍兵. 一種基于有向圖模型的模糊多故障診斷算法[J]. 系統工程與電子技術, 2008, 30(3): 568-571.

LIAN K, HUANG J G, LONG B. Fuzzy multiple fault diagnosis algorithm based on digraph models [J]. Systems Engineering and Electronics, 2008, 30(3): 568-571.

[4] 馬駿, 倪世宏, 解武杰, 等. 改進的強跟蹤飛機舵面快速故障診斷方法[J]. 系統工程與電子技術, 2015, 37(11): 2566-2573.

MA J, NI S H, XIE W J, et al. Fast fault diagnosis of improved strong tracking aircraft actuator [J]. Systems Engineering and Electronics, 2015, 37(11): 2566-2573.

[5] LI H Y, GAO Y B, SHI P, et al. Observer-based fault detection for nonlinear systems with sensor fault and limited communication capacity [J]. IEEE Trans.on Automatic Control, 2016, 61(9): 2745-2751.

[6] DENG W L, QIU D W. State-based decentralized diagnosis of bi-fuzzy discrete event systems [J]. IEEE Trans.on Fuzzy Systems, 2015, 25(4): 2745-2751.

[7] GE X L, PU J K, GOU B, et al. An open-circuit fault diagnosis approach for single-phase three-level neutral-point-clamped converters [J]. IEEE Trans.on Power Electronics, 2017, PP(99): 1-12.

[8] KEMALKAR A K, BAIRAGI V K. Engine fault diagnosis using sound analysis[C]∥Proc.of the International Conference on Automatic Control and Dynamic Optimization Techniques, 2016: 943-946.

[9] SHEN Y H, LU C H. Research on method for information standardized description and transmission in networked fault diagnosis[C]∥Proc.of the International Conference on Computer Science and Applications, 2015: 333-338.

[10] HU M. A unified AC fault diagnosis method for analog circuits based on iterative simulation before test[C]∥Proc.of the IEEE International Conference on Electronic Measurement & Instruments, 2015: 13-19.

[11] DEB S, PATTIPATI K R, RAGHAVAN V. Multi-signal flow graphs: a novel approach for system testability analysis and fault diagnosis [J]. IEEE Aerospace & Electronic Systems Magazine, 1995, 10(5): 14-25.

[12] ZAD S H, KWONG R H, WONHAM W M. Fault diagnosis in discrete-event systems: framework and model reduction [J]. IEEE Trans.on Automatic Control, 2003, 48(7): 1199-1212.

[13] 梁爽,于勁松,唐荻音,等.基于多信號流圖與分支定界算法的故障診斷[J]. 北京航空航天大學學報, 2016, 42(1): 180-186.

LIANG S, YU J S, TANG D Y, et al. Research on fault diagnosis based on multi-signal flow graph and branch-and-bound algorithm [J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(1): 180-186.

[14] PENG Y, REGGIA J A. A probabilistic causal model for diagnostic problem solving part I: integrating symbolic causal inference with numeric probabilistic inference [J]. IEEE Trans.on Systems, Man and Cybernetics, 1987, 17(2): 146-162.

[15] 楊莉,尚勇,周躍峰,等.基于概率推理和模糊數學的變壓器綜合故障診斷模型[J].中國電機工程學報,2000,20(7):19-23.

YANG L, SHANG Y, ZHOU Y F, et al. Probability reasoning and fuzzy technique applied for identifying power transformer malfunction[J]. Proc.of the Chinese Society for Electrical Engineering, 2000, 20(7): 19-23.

[16] PACHECO F, CERRADA M, SANCHEZ R V, et al. A methodological framework using statistical tests for comparing machine learning based models applied to fault diagnosis in rotating machinery[C]∥Proc.of the IEEE Latin American Conference on Computational Intelligence, 2016: 1-6.

[17] CHEN S P. A kind of semi-supervised classifying method research for power transformer fault diagnosis [C]∥Proc.of the IEEE International Conference on Software Engineering and Service Science, 2016: 1013-1016.

[18] ZUQUI G C, RAUBER T W, MUNARO C J, et al. Robust fault detection and diagnosis for multimode processes[C]∥Proc.of the IEEE International Conference on Industry Applications, 2016: 1-6.

[19] CHEN J, YE F, LI Y B. A robust rotary machinery fault diagnosis approach based on entropy fusion and DS theory[C]∥Proc.of the IEEE International Conference on Signal Processing, 2016: 1424-1428.

[20] JIANG Z Y, LI Z W, WU N Q, et al. A Petri net approach to fault diagnosis and restoration for power transmission systems to avoid the output interruption of substations [J]. IEEE Systems Journal, 2017, PP(99): 1-11.

[21] YANG Z M, ZHANG C C, LIU M Z, et al. Graph-based fault diagnosis method for complex electronic systems[C]∥Proc.of the IEEE International Conference on Electronic Measurement & Instruments, 2015: 63-68.

[22] HU Y G, GUO Z L, LI B, et al. Fault diagnosis using directed graph[C]∥Proc.of the IEEE International Conference on Software Engineering and Service Science, 2016: 466-470.

[23] YU G, ZHANG L Z. An intelligent approach for bearing fault diagnosis based on Bayesian networks and alpha-stable distribution[C]∥Proc.of the International Conference on Computational Intelligence and Communication Networks, 2015: 76-78.

[24] ZHANG J B, QI M C, LI B. Hybrid diagnosis of fault tree and Bayesian network in BIW automatic welding production line[C]∥Proc.of the IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference, 2016: 297-300.

[25] U.S. Department of Defense. Basic Dependency Modeling Terminology [EB/OL].[2016-11-01].http:∥www.testability.com/Reference/Glossaries.aspx? Glossary=Dependency Modeling.

[26] WOHL J G. Information automation and the Apollo program: a retrospective [J]. IEEE Trans.on Systems, Man and Cybernetics, 1982, 12(4): 469-478.