基于共軛梯度法和全變差正則化的圖像復原

張彬，孫菁聰，王勝文

(中國傳媒大學理學院，北京 100024)

1 引言

圖像復原的目的是將原始圖像從觀察到的降晰圖像中恢復出來。實際的降晰函數可以看作一個低通濾波器，使得原始圖像的高頻成分受到抑制甚至喪失。這個降質過程可以描述為如下的數學模型：

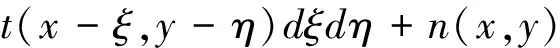
(1)

其中，f(x，y)為原圖像，g(x，y)為觀測到的退化圖像，t(x，y)為空間不變的點擴散函數，n(x，y)為高斯白噪聲。對該模型離散化后，將離散退化圖像、離散源圖像和離散噪聲圖像分別按照列字典序依次排列，可得三個列向量g、f和n，它們滿足如下的線性方程組：

g=T·f+n

(2)

其中T是一個分塊Toeplitz矩陣。

一般來說由于方程(2)是病態的，不能直接求解。因此必須添加一些先驗約束以使問題正則化。為了更好地保留圖像的細節信息，本文以圖像的全變差為約束項，求解下述泛函的極小化問題

(3)

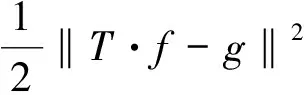
2 全變差函數的離散化和基于共軛梯度法的正則化復原算法

對于二元函數f(x，y)，其全變差TV(f)定義為

在單位正方形的水平區間內插入nx個等分點，在豎直區間內插入ny個等分點，于是有分點(xi，yj)，xi=i·Δx，yj=j·Δy，0≤i≤nx，0≤j≤ny，取f(x，y)在這些離散點的值得離散圖像

將上述圖像按列字典序排列，得向量f。

f=(f0，0f1，0…fnx，0f0，1f1，1…

fnx，1…f0，nyf1，ny…fnx，ny)T

為方便計算，可將面積元素ΔxΔy合并到正則化參數α中，于是Jβ(f)離散化為

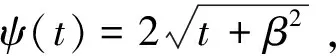
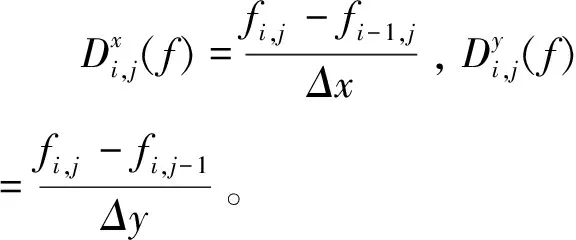
利用方向導數與梯度的關系，可以求得Jβ(f)的梯度。

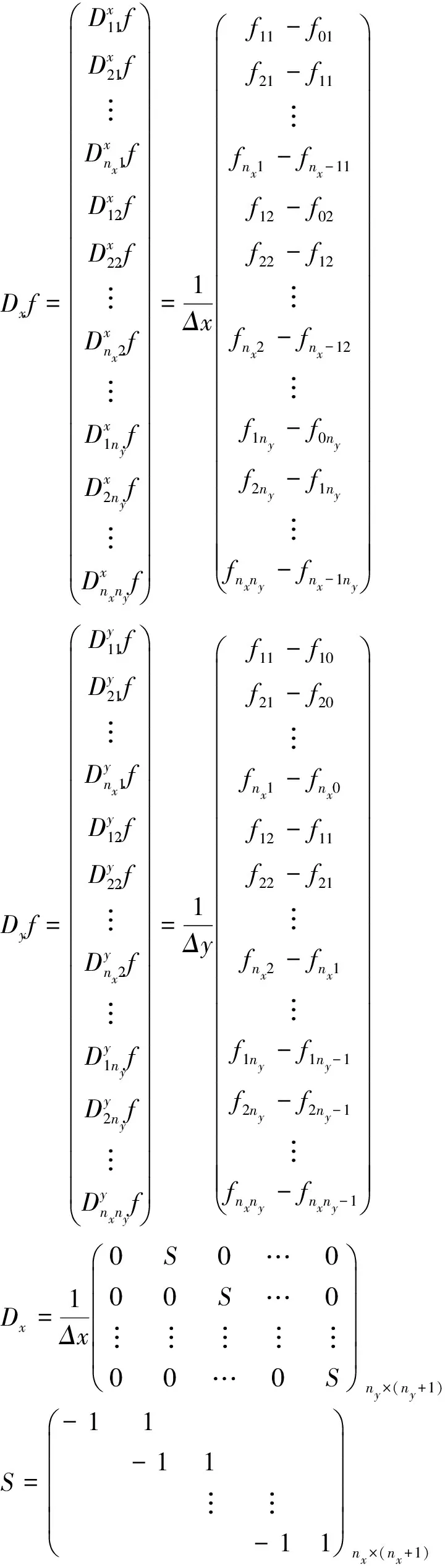
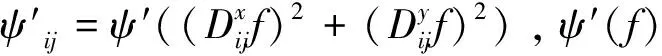
則有

上述梯度計算可按照分塊Toeplitz矩陣與向量乘積的計算.

從(4)式可以得到Jβ(f)的梯度，把它用矩陣表示為

(5)

對基于全變差正則化的極小問題

其梯度為TT·(T·f-g)+α·L(f)

從而該極小化問題等價于求解線性方……