二次時變參數離散灰色預測模型的進一步推廣

金夢迪，劉基偉，張輝

(中國傳媒大學 理學院，北京 100024)

1 引言

由于對可靠小樣本統計的需求日益增長，小樣本預測是一個很重要的課題。多年來，學者們對小樣本非平穩時間序列的預測問題做了深入研究，突出問題是，對于非平穩時間序列，當系統受到干擾的嚴重影響時，過去的可用數據不能如實反映系統的規律。因此，為使預測模型的擾動界變小，引入分數階經典弱化緩沖算子，對原始序列進行微調來提高預測精度；并且通過建立二次時變參數離散灰色模型對實例進行研究驗證。

2 分數階弱化緩沖算子的構造

經典弱化緩沖算子充分考慮每個數據的優先性，而變權弱化緩沖算子只考慮最新一個數據的優先性，所以從綜合利用原有數據信息的角度考慮，經典弱化緩沖算子是一種不錯的緩沖算子。

容易證明，經典弱化緩沖算子的階數越高，越能體現新信息的作用，提高預測質量[2]。但是經典弱化緩沖算子不能實現緩沖作用強度的微調，本文引入分數階弱化緩沖算子。

一階弱化緩沖算子的矩陣形式為：

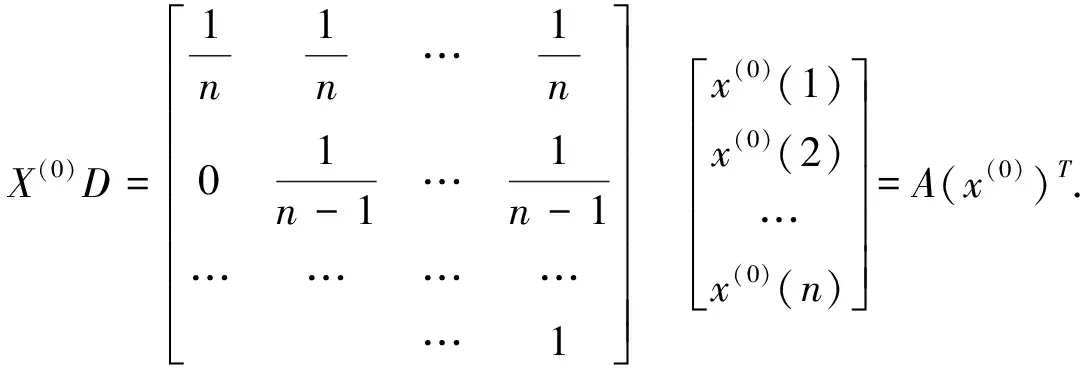
二階弱化緩沖算子的矩陣形式為：

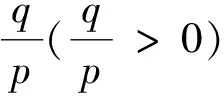
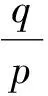
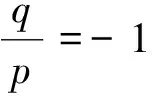
若X(0)為單調衰減序列，因為A(X(0))T≤(X(0))T，A為可逆矩陣，可得A-1A(X(0))T≤A-1(X(0))T，即(X(0))T≤A-1(X(0))T，所以D-1為單調衰減序列的強化緩沖算子；同理D-1為單調增長序列的強化緩沖算子。

若X(0)為震蕩序列，x(0)(l)=max{x(0)(k)，k=1，2，…n}，x(0)(h)=min{x(0)(k)，k=1，2，…n}，

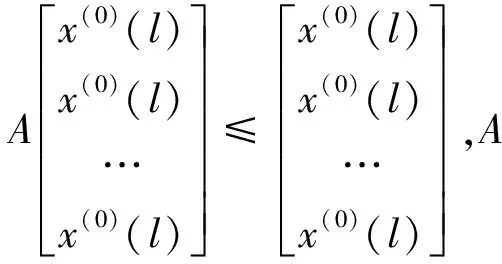
3 二次時變離散參數灰色預測模型介紹

對于實際應用的數據，因為受到外界諸多沖擊因素的干擾而失真。為了能夠準確的挖掘事物規律，針對以往模型使用連續時間響應式進行預測產生的跳躍性誤差，本文使用時變參數離散灰色模型。……