移動區域中的電場問題的研究

劉小妹，閆述濤

(中國傳媒大學理工學部，北京 100024)

1 引言

電磁推進系統是以導軌和電樞為主要組成部分，通過對導軌兩端施加電壓，使導軌內產生電流，在電流和導軌間磁場的共同作用下，進而產生作用在電樞上的洛倫茲力，通過洛倫茲力對電樞的作用來加速拋體運動的裝置。移動過程中，導軌與電樞接觸面隨時間變化，導致電場、電流也隨之變化。求解問題模型如圖1，其中最外層是空氣層，中間為兩條導軌，導軌中間是滑動的電樞，在導軌兩端通電，由導軌與電樞構成一個閉合回路。

2 理論模型

在求解區域中，我們將在兩個導軌上分別添加適當電壓，我們通常給予150V和-150V的電壓，利用磁矢量A和標量電位u表示的麥克斯韋方程來求解電場與磁場的分布。已知麥克斯韋方程的微分形式為

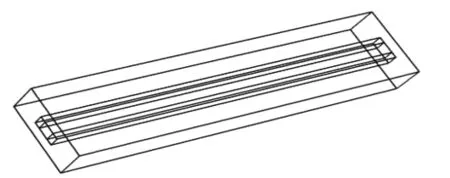
圖1 電磁軌道推進系統模型

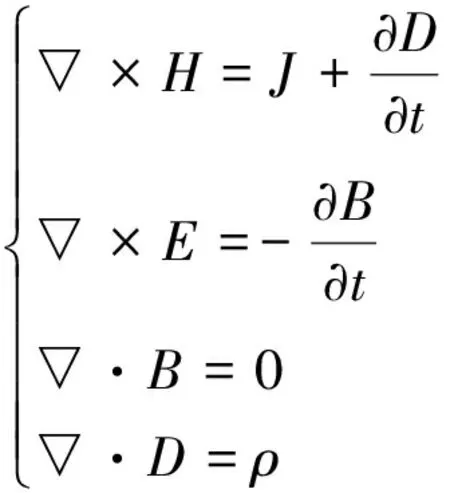
(1)

又有

D=εE，B=μH，J=σE

其中，H：磁場強度；J：電流密度；D：電位移；E：電場強度；B：磁感應強度；ρ：自由電荷體密度；μ：磁導率；σ：電導率；ε：介電常數，這里我們忽略電位移的影響，將問題簡化為渦流方程，那么(1)式變為：

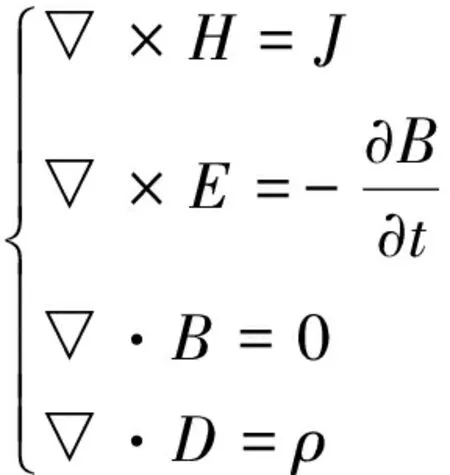
(2)

因此，渦流場方程可以從(2)式中導出，選擇磁矢量A和標量電位u組成的電磁位對，將含有運動電樞的麥克斯韋方程組變換為：

▽·(-(σ▽u))=0

(3)

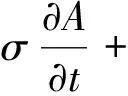
(4)

(3)式和(4)式可以視作渦流場控制方程的統一形式。在圖1中，在導軌和電樞及導軌間的空氣中需要描述電場和磁場，因此(3)式和(4)都需要用到，而在最外空氣層中，只需描述磁場即可，因此我們只需要用到(3)式。

在忽略了電位移的影響下，問題中還涉及到邊界的問題，我們需要處理好在邊界上電場與磁場的條件，我們設在邊界上：