建造高塔

李佩寧

最優解問題是從數學，尤其是幾何學中衍生出來的概念。它原本指的是使線性規劃的目標函數達到最大值或最小值的可行解，和對該解存在與否、如何求得的數理演繹。而在一般性的問題解決中，最優解指的是：對某個可以量化的問題，在給定的有限條件下，對最佳辦法是否存在以及如何設計并執行的問題的探討。最優解問題的答案可能不唯一，也可能沒有答案。

最優解問題在生活中的核心體現，往往是運籌學和博弈論所要解決的問題。運籌學主要研究經濟活動和軍事活動中能用數量來表達的有關策劃、管理方面的問題，可以根據問題的要求，通過分析、運算，得出各種各樣的結果，最后提出綜合性的合理安排，以達到最好的效果。隨著社會的進步與發展，運籌學的有些內容已經在日常生活中泛化和深入。博弈論則是運籌學的分支，主要研究公式化了的激勵結構間的相互作用，是研究具有斗爭或競爭性質現象的數學理論和方法。博弈論考慮游戲中個體的預測行為和實際行為，并研究它們的優化策略。運籌學和博弈學都涉及到對最佳辦法的尋找，即數學模型的最優解。

一、課程重點

本課程通過讓學生了解工程試驗，培養學生對工程設計的認識。在尋找最優解的過程中，引導學生鍛煉對多種解決方法進行歸類和分別處理的能力，培養對細節的認識、觀察以及綜合理解能力，并對運籌學和博弈論形成一些感性認識。

【涉及領域】工程、物理學、建筑學

【建議年級】小學中年級

【建議時間】125分鐘

二、課程任務

在給定材料數量的前提下，要求學生運用數學計算和推理，通過實際動手，嘗試尋找最佳方案。在具體問題具體分析中，以及親自動手實踐中，引導學生動手動腦，就最佳設計的方式和思路展開討論。

三、課程步驟

1.導入（15分鐘）

第一步，闡述極限和最優解的概念。通俗地講，極限是某個事物或某類事物發展的上限或者下限，是無法跨越的一種程度。極限值有可能是達不到的卻可以無限趨近的。最優解，是指在規劃中產生所需要的最大值或最小值的那個解決方案，有的情況下可以是多個。

教師可以舉例說明數學上的極限，以及什么是生活中運籌問題的最優解。例如，先說一個小數0.1，然后讓學生說出一個比0.1小但是比0大的數，然后讓下一個學生說出比之還小但是比0大的數字，以此類推。然后，詢問學生這樣的數字可以一直小到多少，能出現多少個這樣的數字。當學生回答是無數個之后，教師解釋：這樣的數字是永遠到達不了0那么小的，但是會越來越小，不斷地接近0，0就是這一串數字變化的極限。

至于生活中運籌問題的最優解，教師可以列舉學生從早晨起床到上學的整個步驟，讓學生思考可以由幾種最佳的順序完成。其中，可能有一種或者多種在最短時間內完成多項任務的安排方式，而任意一種最佳的時間安排方式，其實就是一種最優解。

第二步，強調資源的有限性，并提出對有限資源利用的建議。本次課程中，材料都是有限的，并且在尋找最佳方案的前提下可能會需要反復利用。所以，有必要進行合理規劃，考慮在實驗過程中解決材料的可重復利用問題。

2.宣布任務一及評價量規（10分鐘）

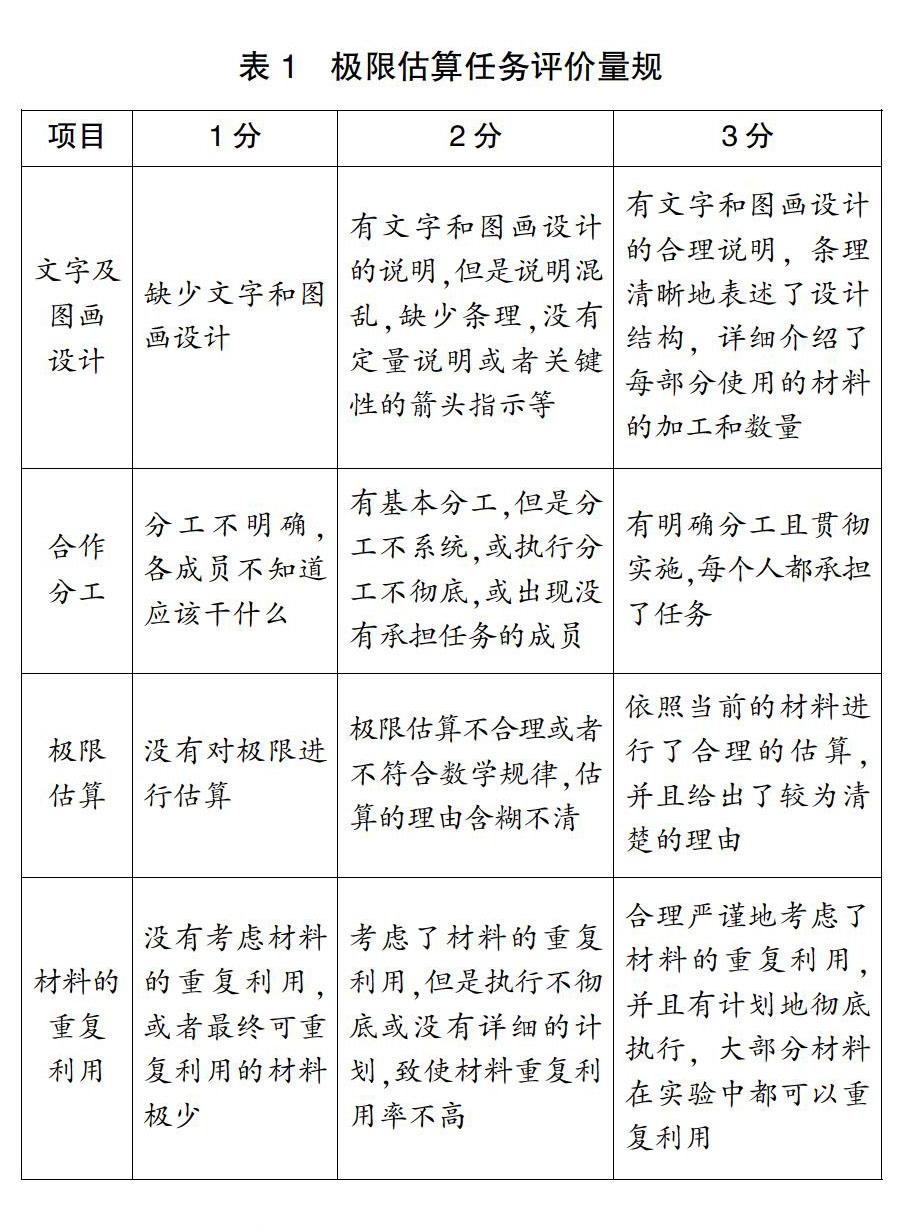
【宣布任務】首先，通過觀察判斷給定材料（數量有限，嚴格按照給定的數量進行制作）能夠制作高塔的最高極限是多少，并要說出如何得出這個極限;之后，使用給定的材料進行兩次實驗，通過實驗不斷接近自己觀察判斷出的極限值，同時修正制作方式。在此過程中，學生必須要考慮材料的重復利用。宣布任務后，呈現評價量規（見表1）。

【材料】30根吸管、剪刀、60厘米長的膠帶、10把尺子（建議每組2把）。

在宣布任務和評價量規后，教師可以繼續提出以下問題。

（1）各組計算或估算的極限各是多少？如果極限相同，各自的設計是否一致？

（2）極限實際能否達到？在實際操作中會遇到哪些困難？請列舉出來。

提問后，給各組少量時間進行溝通準備。每個人都要寫下自己的想法和實驗計劃，然后小組討論執行什么樣的實驗計劃。

3.任務一的執行（20分鐘）

正式執行制作任務。要求學生依照評價量規，考慮以下問題。

（1）小組最終同意的極限是多少？

（2）為了盡可能接近這個極限，在設計中如何利用材料？

（3）為了進行多次實驗，如何使用吸管？如何使用膠帶？吸管和膠帶怎樣連接？連接怎樣保持穩固性？

（4）實驗執行時應該注意哪些細節？

（5）估算極限值時，是否真正考慮了所有的可能性？能否通過對材料的進一步加工而改變極限值？

（6）小組的分工如何？

4.總結和反思（25分鐘）

全部小組完成任務后，組織討論以下問題。

（1）小組對極限值的估計進行了幾次，出現了幾個極限值？是什么理由推翻了之前的估算？

（2）在實驗所產生的設想中，接近理論極限值的最大實際困難是什么？

（3）如何在實驗時盡力做到重復利用現有材料？

5.宣布任務二及評價量規（10分鐘）

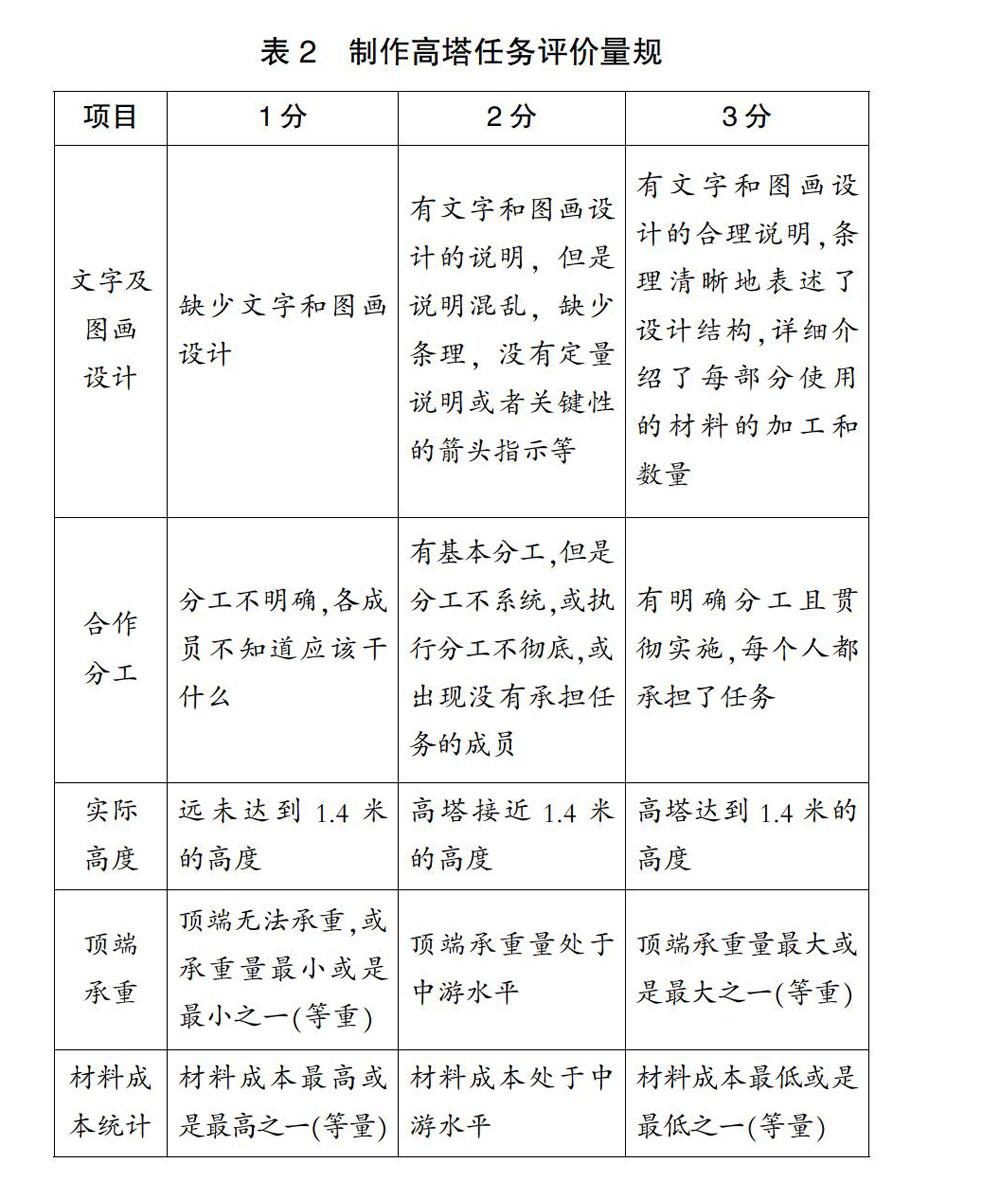
【宣布任務】使用給出的材料實際制作一個1.4米高的塔（底部不得粘在桌面上），必須保證能立起，能承受一定的重量，并且盡量節省材料成本，最后看哪個組制作的高塔能實現“物美價廉”（教師自行給材料賦予一定的成本，例如買一把尺子要花多少錢）。需要說明的是，學生要進行文字和圖畫的設計。宣布任務后，呈現評價量規（見表2）。

【材料】30根吸管、剪刀、60厘米長的膠帶、10把尺子（建議每組2把）。

需要特別說明的是，為了防止學生針對評價量規的最后兩項做出“專注于一項評分而放棄另一項”的不被鼓勵的設計，教師可以酌情對最后兩項評分進行必要的加權處理，以使學生在完成“增加承重”和“減少成本”兩項任務時的評分回報率大體相仿。

6.任務二的執行（20分鐘）

正式執行制作任務。要求學生依照評價量規，考慮以下問題。

（1）如何保證高塔不倒下？如何保證高塔的傾斜角最小？

（2）為了盡可能接近高度極限，在設計中如何利用材料？

（3）哪些設計是為了穩固？哪些設計是為了增高？

（4）什么因素導致制作的高塔產生傾角？

（5）小組的分工如何？

7.總結和反思（25分鐘）

全部小組完成后，組織討論以下問題。

（1）目前哪個小組得到了“最優解”？是否還有繼續改進的空間？

（2）為了達成獲得最優解的目的，還有什么相關內容需要被提前測量？比如，桌面的微小起伏是否會影響最終的結果？

（3）能否通過對材料的再進一步加工而改良現有的最優解？

（責任編輯? ?張慧籽）