內蒙古奈曼旗農作物春播—出苗期降水量預測模型建立

張華，李世華，董佳蕊，劉浩，丁曉華

摘要：根據天氣學原理和專家研究結果，大氣環流是影響中國天氣氣候的重要因素，因此，在進行月以上氣候預測時，必須分析大范圍環流形勢和影響大范圍環流形勢變動的因子。該文應用SPSS因子分析法對奈曼旗春播及出苗期（4-6月）降水進行分析預測研究，結果從歷史擬合和預測試報結果表明，均超過0.01的顯著性檢驗標準，總體上預測效果較好，可以投入業務應用。

關鍵詞：奈曼4-6月降水；因子分析；預測方法研究

張 華，李世華，董佳蕊，等. 內蒙古奈曼旗農作物春播-出苗期降水量預測模型建立[J]. 農業工程技術，2017，37（35）：14-16.

奈曼旗位于科爾沁沙地南緣，屬北溫帶大陸性季風干旱氣候，平均海拔高度450 m，受大陸季風氣候影響，各季降水分布差異較大。春播及出苗期（4-6月）降水雖在全年中所占比重相對較小，但對農業生產起著至關重要的作用，往往由于降水偏少及時空分布不均等造成的春播及出苗期干旱災害等會給農業生產等帶來嚴重影響[2-3]。所以說，春播及出苗期是農業生產用水的關健季節，因此，提前作出春播及出苗期降水的長期趨勢預測預報[4]，為當地黨政領導提供最具科學依據的決策氣象服務有十分重要的意義。

1 預報因子或指標的選取

1.1 資料與方法

根據天氣學原理和專家研究結果，大氣環流是影響全國天氣氣候的重要因素[1]，因此，在進行月以上氣候預測時，必須分析大范圍環流形勢和影響大范圍環流形勢變動的因子[4，11]。表示大范圍環流形勢的因子有：太平洋、大西洋副熱帶高壓、北美、北非副高、極渦面積、強度、歐亞、亞洲緯向、徑向環流等，影響大范圍環流變動的因子有太陽黑子活動指數、海表溫度等[5]。

本研究選取國家氣候中心網上實時更新的北半球副高面積指數等74個環流特征量因子。利用SPSS皮爾遜（Pearson）相關系數及向后回歸剔除顯著性相對較差因子的方法[14]，計算了環流因子和太陽黑子分別與4-6月降水量的相關性，選取相關檢驗顯著的因子作為降水預測方程的因子（見表1），因子資料和降水資料長度為1961-2015年。4-6月降水預測方程的建立，選用多元回歸方法[13，15]。

1.1.1 相關分析。相關分析是研究變量間密切程度的一種常用統計方法[7-8]。相關系數是描述相關關系強弱程度和方向的統計量，本分析應用皮爾遜（Pearson）相關系數法將74個環流因子上年值及當年值分別與4、5、6月降水量進行相關系數分析。

1.1.2 多元回歸。研究幾個自變量的變化對因變量的影響，可以用多元回歸方法，亦稱多重回歸。當多個自變量與因變量之間是線性關系時，所進行的回歸分析就是多元線性回歸[9-10]。

y為因變量，x1，x2···xk為自變量，并且自變量與因變量之間為線性關系時，則多元線性回歸模型為：y=b0+b1x1+b2x2+···+bkxk+e，其中，b0為常數項，b1，b2···bk為回歸系數，b1為x1，x2···xk固定時，x1每增加一個單位對y的效應，即x1對y的偏回歸系數；同理b2為x1，x2···xk固定時，x2每增加一個單位對y的效應，即，x2對y的偏回歸系數，等等。模型描述為：y=b0+b1x1+b2x2+···+bkxk+e[13]。

建立多元性回歸模型時，為了保證回歸模型具有優良的解釋能力和預測效果，應首先注意自變量的選擇，其準則是：

①自變量對因變量必須有顯著的影響，并呈密切的線性相關；②自變量與因變量之間的線性相關必須是真實的，而不是形式上的；③自變量之間應具有一定的獨立性，即自變量之間的相關程度不應高于自變量與因變量之因的相關程度；④自變量應具有完整的統計數據，其預測值容易確定。

1.2 因子分析

經過選取55年（1960-2014）、45年（1970-2014）、35年（1980-2014）因子資料，與55年（1961-2015）、45年（1971-2015）、35年（1981-2015）奈曼旗本站4-6月降水量進行相關分析及向后回歸剔除顯著性相對較差因子，篩選出表1所示因子作為分別預測4、5、6月方程的因子。

2 預報方程的建立

專家分析和篩選分析表明，隨著近百年全球氣候的變化[6]，大氣環流的平均狀態在上世紀80年代有明顯的調整[12]。經計算顯示，奈曼本站的4-6月降水量與55年、45年、35年因子之間的相關系數的大小也存在明顯的階段性，其中二十世紀70年代以后的45年要比前60年代以后55年和80年代以后35年相關程度高，因此，我們選擇了45年資料的1980-2011年作為預測方程建立的時段，將2012-2014年作為預測檢驗時段。

應用SPSS軟件的分析多元線性回歸功能分別建立4、5、6月份降水量預測方程。

2.1 4-6月預測方程

建立回歸模型：

根據各月多元回歸系數代入得如下回歸方程：

Y4=384.148-1.982X1-3.756X2-0.547X3+ 1.047X4+0.331X5+0.987X6-0.912X7+0.454X8-0.912X9

Y5=315.506-0.529X1+0.440X2-0.976X3-1.209X4-1.413X5-0.332X6+0.767X7-0.947X8-0.851X9

Y6=-54.537+3.086X1+0.108X2+1.313X3+1.112X4-0.515X5+0.362X6-2.466X7+3.102X8

2.2 回歸方程的顯著性檢驗

表2-1 4、5、6月模型匯總表R分別為0.928、0.913、0.925，說明各月模型擬合度較高，4月92.8%的預測、5月91.3%的預測、6月92.5%的預測可以用相應模型來預測，表2-2回歸模型的方差分析表，4、5、6月的顯著性概率均為0.000<0.001。其中4月F（0.05，9，22）值為2.34，F（0.01，9，22） 值為3.35，F（0.001，9，22） 值為4.99，5月F（0.05，9，22）值為2.37，F（0.01，9，22） 值為3.40，F（0.001，9，22） 值為5.11，6月F（0.05，8，23）值為2.37，F（0.01，8，23） 值為3.41，F（0.001，8，23） 值為5.09，因此各月回歸方程相關非常顯著。（F值用Excel中FINV（ ）函數求得）。

2.3 方程的歷史擬合檢驗

利用表2-3中的因子方程，擬合了1980-2012年歷年4、5、6月的月降水量。圖1-圖3給出了各月份因子預測的降水實況的年際變化圖。

從各月預測方程的擬合相關系數看，擬合效果顯著，均超過0.01的顯著性檢驗標準，相關系數見表3。

2.4 2013-2015年4-6月降水預測檢驗

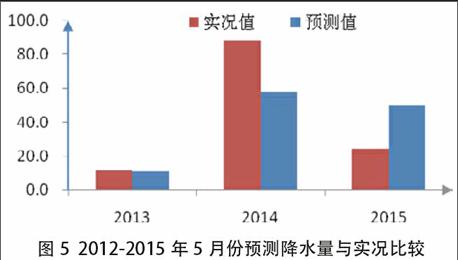
利用建立的4月、5月、6月預測方程，對2013-2015年4-6月降水量進行了試報檢驗。結果顯示（圖4-圖6），4月的預測效果最好，5月的預測效果排第二，6月的預測效果第三。

綜合以上預測方程的歷史擬合和預測試報結果表明，總體上預測效果較好，預測準確率4-5月較高，6月次之，4-6月降水量預測模型可以用于業務應用，但6月模型還有待進一步實踐檢驗，我們將在業務預報和服務中邊應用邊檢驗，逐步優化和改進預報方程參數，逐步提高預測準確率。

參考文獻

[1] 魏鳳英. 現代氣候統計診斷預測技術[M]. 北京：氣象出版社，1999.

[2] 李克讓，郭其蕰，張家誠等. 中國干旱災害研究及成災對策[M]. 鄭州：河南科學技術出版社，1999.

[3] 中國國家質量監督檢驗檢疫總局，中國國家標準化管理委員會. 中華人民共和國國家標準GB/T 20481-2006.氣象干旱等級[M]. 北京：中國標準出版社，2006.

[4] 王永光，龔振淞，許 力，等. 中國溫度、降水的長期氣候趨勢及其影響因子分析[J]. 應用氣象學報，2005，Vol.15（增刊）.

[5] 國家氣候中心網站，http：//ncc.cma.gov.cn/cn/.

[6] 魏鳳英，韓雪，王永光，等. 中國短期氣候預測的物理基礎及其方法研究[M]. 北京：氣象出版社，2015.

[7] 吳洪寶，吳蕾著. 氣候變率診斷和預測方法[M]. 北京：氣象出版社，2005.

[8] 黃嘉佑. 氣象統計分析與預報方法（第3版）[M]. 北京：氣象出版社，2004.

[9] 李湘閣，胡凝，等. 實用氣象統計方法[M]. 北京：氣象出版社，2015.

[10] 黃嘉佑，李慶祥，等. 氣象數據統計分析方法[M]. 北京：氣象出版社，2015.

[11] 孫照渤，陳海山，譚桂容，等. 短期氣候預測基礎[M]. 北京：氣象出版社，2010.

[12] 李俊亭，竹磊磊，李曄，等. 河南省春季降水的氣候特征及干旱預測[J]. 人民黃河，2010（12）.

[13] 于秀林，任雪松. 多元統計分析[M]. 北京：中國統計出版社，1999.

[14] 郝梨仁，樊元郝，哲 歐. SPSS實用統計分析[M]. 北京：中國水利水電出版社，2002.

[15] 何曉群. 應用回歸分析[M]. 北京：中國人民大學出版社，2001.