中國象棋博弈系統實現的關鍵技術探索

肖秀春 劉澤偉 陳柏桃

摘要

棋局表示、著法生成、搜索算法、局面評估等是中國象棋人機博弈系統的關鍵，它決定了一個象棋博弈系統的優劣本文重點從優化中國象棋人機博弈系統性能的目的出發，圍繞該系統的實現，探索其若干基本理論問題。同時，探討了中國象棋人機博弈樹的搜索技術;在此基礎上，探索局面估值函數的建立方法，以及在各類搜索算法基礎之上的優化思路。

【關鍵詞】中國象棋 博弈 棋盤表示 著法生成 博弈樹搜索

1 引言

中國象棋是我國一門古老的博弈游戲，其中蘊含了大量關于運籌，謀略的思想。人機對弈是人與計算機之間的決策計算過程，它是人工智能的一個研究分支，它的研究為人工智能帶來了很多重要的方法和理論，產生了廣泛的社會影響和學術影響。

要實現人機對弈的功能，首先要有能夠反映棋盤信息的數據結構，根據規則產生合法著法，并且在輪到計算機走子時，計算機能夠搜索到對己方最為有利的著法。我們可以用一棵“博弈樹”來表示下棋的過程，樹中的每一個節點代表棋盤上的一個局面，對于每一個局面根據不同的著法又產生不同的局面，如此直到葉節點。根據規則，可以可靠地判斷輸贏，假設每次計算機都能搜索到最優局面，那么計算機將處于不敗的地位。但就目前而言，計算機能搜索到的層數有限，因此需要一個評估函數來判斷局面的好壞，這樣，計算機便能通過評估函數選擇對自己最為有利的著法。

從結構上，可以將一個人機對弈系統分為棋盤表示，著法生成，搜索算法以及局面評估幾個方面。擁有了以上這些，計算機便能實現基本的對弈功能。與人類相比，計算機還未能根據局面的情況制定作戰計劃，它擅長的是計算，因而對于棋力的增強，則有賴于搜索算法及局面評估的結合，隨著搜索算法的不斷改進，搜索過程中剪枝效率越高，搜索的層次越深;同時，對于搜索結果進行的局面評估越精確，搜索得到的著法便越好，計算機的棋力也大幅度提升。

2 棋盤表示及著法生成

無疑地，棋盤表示是中國象棋人機博弈系統著法生成的基礎。合適的棋盤表示不僅有利于著法生成中各個搜索節點的存儲，也將有利于局面評估函數對當前節點的評價。

2.1 棋盤表示

中國象棋的棋盤為9×10的矩形，一般采用9×10的二維數組表示。但是，這種表示方法將不利于棋盤邊界的判斷。基于邊界的判斷考慮，也可以采用16×16的擴展棋盤來表示。通常，采用一個大小為256的一維數組來表示的帶擴展邊界的棋盤，對于棋子，數字0表示空位（即該位置沒有棋子），數字8～14依次表示紅方的帥、仕、相、馬、車、炮和兵;數字16～22依次表示黑方的將、士、象、馬、車、炮和卒。因此棋盤的初始局面可以表示為：

int ChessBoard[256]={

0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，

0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，

0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，

0，0，0，20，19，18，17，16，17，18，19，20，0，0，0，0，

0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，

0，0，0，0，21，0，0，0，0，0，0，21，0，0，0，0，

0，0，0，22，0，22，0，22，0，22，0，22，0，0，0，0，

0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，

0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，

0，0，0，14，0，14，0，14，0，14，0，14，0，0，0，0，

0，0，0，0，13，0，0，0，0，0，0，13，0，0，0，0，

0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，

0，0，0，21，0，21，0，21，0，21，0，21，0，0，0，0，

0，0，0，12，11，10，9，8，9，10，11，12，0，0，0，0，

0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，

0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0};

這里判斷是否超出邊界非常簡單，利用如下所示的數組，判斷棋子所在位置是否為0就行了。

int IsInBoard[256]={

0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，

0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，

0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，

0，0，0，1，1，1，1，1，1，1，1，1，0，0，0，0，

0，0，0，1，1，1，1，1，1，1，1，1，0，0，0，0，

0，0，0，1，1，1，1，1，1，1，1，1，0，0，0，0，

0，0，0，1，1，1，1，1，1，1，1，1，0，0，0，0，

0，0，0，1，1，1，1，1，1，1，1，1，0，0，0，0，

0，0，0，1，1，1，1，1，1，1，1，1，0，0，0，0，

0，0，0，1，1，1，1，1，1，1，1，1，0，0，0，0，

0，0，0，1，1，1，1，1，1，1，1，1，0，0，0，0，

0，0，0，1，1，1，1，1，1，1，1，1，0，0，0，0，

0，0，0，1，1，1，1，1，1，1，1，1，0，0，0，0，

0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，

0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，

0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0};

2.2 著法生成

著法生成主要是用來判斷用戶的著法是否正確，以及生成計算機的所有著法，用以從中選取最好的著法。對于象棋的各個兵種，我們可以將其各個合理的著法存儲起來，在生成時直接取出來就可以了，這樣就省去了很多工作，提高了系統的性能。

3 搜索算法

3.1 最小一最大搜索及負極大值搜索

對于博弈雙方，每方都在尋求對己方局面有利的著法。假設黑方（為討論問題方便，可假定為黑方為對弈的人，紅方為計算機）贏的局面評估函數分值為負無窮，紅方贏的局面評估函數分值為正無窮，那么，黑方肯定選擇當前評估函數分值較小的著法而紅方應對時，則選擇當前評估函數分值較大的著法。如此交替，即是最小一最大搜索。于是，對于計算機來說，其搜索最有利于己方著法時，必須考慮對方的應對著法，其搜索目標為使得經過交替最小一最大搜索，最終得到當前局面的最小評估值。最小一最大搜索原理可如圖1所示。

圖中展示了黑方當前可以有A、B兩種著法，對應黑方的著法A、B，紅方對應的著法分別為（C，D）和（E，F），其對應的當前局面評估函數分值分別如上圖所示。顯然，當黑方選擇著法A的話，那么紅方肯定會回應D，使估分變為5（紅方有利）。但是如果黑方選擇著法B，那么紅方即使選擇最佳著法E，其估分還是-4（黑方有利）。可以看到，每次遞歸時，走子方改變，選擇方式也相應改變，我們可以將其優化為負極大值搜索，即每次遞歸時將返回值轉為負值，以反映當前局面的更改。偽代碼如下：

int NegaMax（int depth）

{

int best=-無窮大;

if（depth<=0）

return評價值;

調用著法生成函數，生成所有合法著法;

while（生成的著法）

{

試走一個著法;

value=-NegaMax（depth-1）;

撤銷該著法;

if（value>best）

best-value;

}

return best;

}。

3.2 Alpha-Beta搜索

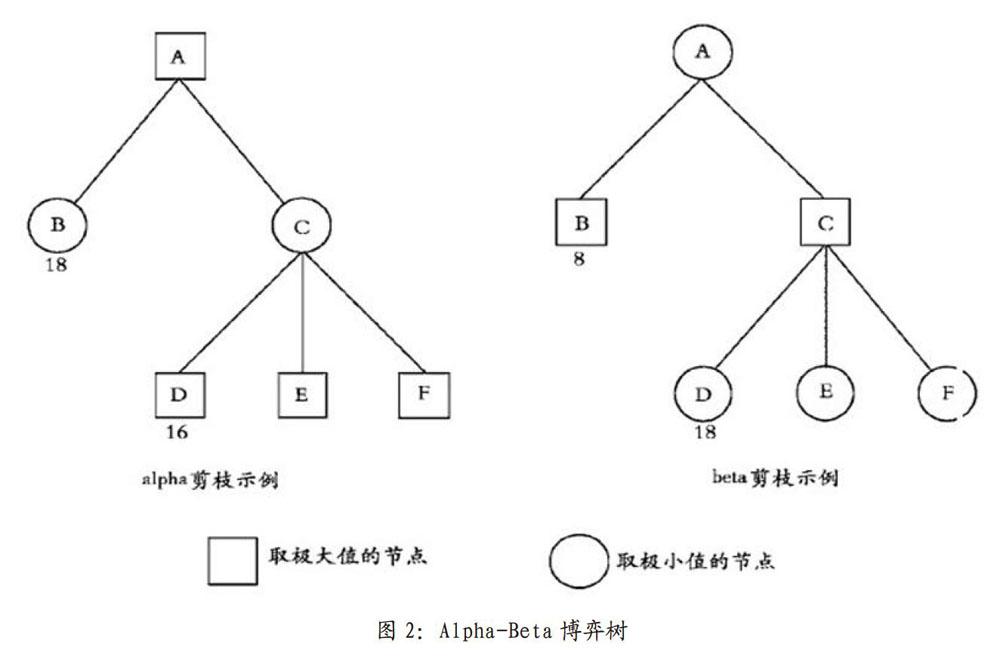
隨著搜索深度的增加，局面是呈指數級增長的，所以在有限的時間內，計算機搜索的層數很淺。而計算機要找到更好的著法，搜索的層數應該盡可能深。因此在搜索過程中，應及時停止擴展那些已無必要再擴展的子節點，即相當于剪去博弈樹上的一些分枝。如圖2所示。

圖2中左邊部分由于節點C取極小值，可以判斷C的值將小于或等于16;而節點A的值為Max（B，C）=18，因此我們不再需要評估節點C的其他節點E、F便可以得出父節點A的值了，這種剪枝策略稱為Alpha剪枝。

同樣，如圖2右邊部分所示，我們可以判定節點C的值將大于或等于18，而節點A為Min（B，C）=8，因此我們也不再需要評估節點C的其他節點的值，這種剪枝策略稱為Beta剪枝。將Alpha剪枝及Beta剪枝加入負極大值搜索便得到Alpha-Beta搜索算法。偽代碼如下：

int A1phaBetaSearch（int alpha，int beta，intdepth）

{

if（depth=0）

return局面評價函數;

調用著法生成子函數，生成所有著法;

for（每個生成的著法）

{

在博弈樹中，取出一個著法;

int value=-A1phaBeta（-beta，-alpha，depth-1）;

在博弈樹中，剪枝一個著法;

if（value>=beta）

break;

if（value>alpha）

alpha=value;

}

return alpha;

}

這就是Alpha-Beta算法，只要有一步好的著法，就可以淘汰很多沒必要搜索的節點，包括節點之下的子樹，使得搜索效率大為提高。

3.3 MID搜索

我們也可以通過一個估算值（g，g+1）作為窗口來進行探測，設定一個上界upperbound和一個下界lowerbound，如果結果大于g，則修改lowerbound，如果小于g，則修改upperbound，如此反復，不斷修改邊界值，知道upperbound和lowerbound收斂于一點。偽代碼如下：

int MTD（）

{

g=初始值;

upperbound=INFINITY;

lowerbound=-INFINITY;

while（lowerbound

{

if（g==lowerbound）

beta=g+1;

else

beta=g;

g=AlphaBeta Seach（beta-1 ，beta，nDepth-1）

if（g

upperbound=g;

else

lowerbound=g

}

returng;

}

4 局面評估

一般而言，都是通過局面評估來判斷著法的好壞。如果把紅方的價值總和設為RedValue，黑方價值總和設為BIackValue，那么Value=BIaekValue-RedValue，就是對于黑方而言的局面的情況。以上分析表明，對于局面評估，著法價值的計算非常重要。我們可以從以下若干角度對著法價值進行計算。

4.1 子力價值

子力價值即是博弈雙方各有哪些棋子，以及價值如何。根據文獻[5]，可以讓一個車的價值為500，一個馬的價值為300，一個兵的價值為100等等，而將的價值設為無窮大或計算機所能表示的最大的數值。

4.2 機動性及對棋盤的控制

機動性值是棋子的活動范圍的度量，通常棋子的活動范圍越大，其機動性也越好，而對棋盤的控制范圍則是一個棋子的合法著法的范圍內，可以通過雙方控制該位置的棋子數量及棋子價值來決定哪方的機動性占優。

4.3 棋子位置

對于同一個棋子，位置不同，其價值也有所不同，比方說，過河卒子要比未過河的價值高得多。可以給每個不同的兵種在棋盤上的各個位置給出經驗評估值，以確保評估的準確性。

5 性能優化

5.1 迭代深化

在搜索過程中對搜索樹作出裁剪，可以有效地降低計算機的搜索時間，從而增加計算機搜索嘗試。對搜索樹剪枝的關鍵在于能夠搜索到好的著法，否則裁剪效率很低。通常，可以通過一個歷史啟發表來存儲搜索過的好的著法，這大大增加了剪枝的效率。剪枝的效率越高，可使得算法迭代層次越深。

5.2 靜態搜索

在下棋的過程有時會遇到這種情況，就是計算機搜索的層次不夠深，因而有些厲害的殺著可能搜索不出來，這就導致棋力下降。我們在局面發生震蕩的時候加深搜索的層次，直到局面沒有吃子或者將軍的情況，這較大幅度地提高象棋的棋力。

6 結束語

博弈理論與人工智能的研究有著相互推動的作用：博弈理論對于人工智能研究的發展提出要求;人工智能的研究成果反過來可以應用于博弈系統實踐。

本文對計算機博弈理論進行了研究，在深入研究了計算機中國象棋理論基礎上，探討了中國象棋人機對弈系統的設計原理。但是用Alpha-Beta搜索算法或其變種以及啟發式搜索的方法，采用局面估值函數對各搜索節點進行估值，這樣人為的主觀因素很強，而要克服這個問題，則需要計算機進行自學習，以取得更高的獨立性及自適應性。

參考文獻

[1]王驕，王濤，羅艷紅.徐心和.中國象棋計算機博弈系統評估函數的自適應遺傳算法實現[J].東北大學學報，2005，26（10）：949-952.

[2]危春波.中國象棋博弈系統的研究與實現[D].昆明理工大學碩士學位論文，2008.

[3]徐心和，王驕.中國象棋計算機博弈關鍵技術分析[J].小型微型計算機系統，2006，27（06）：962-969.

[4]劉淑琴，劉淑英.基于博弈樹搜索算法的中國象棋游戲的設計與實現[J].自動化與儀器儀表，2017（10）：96-98.

[5]金朋，馮速.博弈樹搜索算法概述[J].計算機系統應用，2009（09）：203-207.

[6]蔡屾.一種中國象棋機器博弈剪枝策略的改進方法[J].國外電子技術，2016，35（03）：47-49.

[7]郝卿，黎利輝.基于 Android的中國象棋局域網博弈平臺的設計與實現[J].廣西民族師范學院學報，2017，34（03）：145-148，113.