非航海用DDM向航海應用轉換的方法
曹鴻博,張立華,黃文騫,賈帥東,劉現鵬
(1. 海軍大連艦艇學院海洋測繪系,遼寧 大連 116018; 2. 海軍大連艦艇學院海洋 測繪工程軍隊重點實驗室,遼寧 大連 116018; 3. 海軍出版社,天津 300450)
數字水深模型(digital depth model,DDM)是對海底表面高低起伏形態的數字化模型表達,直接決定了海底地形地貌表達的準確性和艦船航行的安全性[1-2]。從應用服務的顯著性差異出發,DDM可分為航海用DDM和非航海用DDM[3]。航海用DDM主要是對離散的原始水深數據構建不規則三角網結構的數據模型,以保證艦船航行安全[4-5];非航海用DDM則通常采用處理后的內插值作為模型點水深值,并且構建規則網格結構的數據模型,以表達真實的海底地形地貌。非航海用DDM一般采用當前主流的網格模型數據結構[6],在海洋工程、海上考古、海洋地質調查與資源開發等領域存在著廣泛的應用[7-8]。
目前,航海用DDM和非航海用DDM在水深選取和模型構建上有著不同的方法,導致兩者之間不能真正實現水深數據的共享[9]。當前,由于海上水深測量具有高投入、長周期等特點,在不同部門、行業之間進行水深數據的共享、互用是一個必然的趨勢[10]。長期以來,為非航海領域服務的水深數據一般采用的是內插水深,并未顧及在航海應用中所選取的水深需要遵守“取淺舍深”的水深綜合原則[2];另外,非航海用DDM所采用的網格模型數據結構本身具有削峰填谷的性質,而且隨著網格尺度的增大,削峰填谷程度越甚[11],從而導致所構建的非航海用DDM表面存在水深漏淺的現象,給艦船的安全航行帶來重大隱患。上述都是基于人工經驗的方法定性地描述了非航海用DDM在應用于艦船航海時所存在的安全性問題,但如何對這種不安全性進行定量描述,以使非航海用DDM能夠滿足艦船航海上的安全需求則有待研究。2015年,張立華等引入了水深不確定度的概念,首次提出采用深度保證率指標定量評估DDM在航海上的這種安全性,解決了以往單靠人工經驗法在評估航海安全性上存在無定量指標的不足,并且提出了DDM滿足艦船安全航行時深度保證率指標需要達到97.5%的要求[4]。2015年,賈帥東試驗驗證了非航海用DDM的模型點水深值采用距離反比加權時,多格網尺度下的非航海用DDM的深度保證率一般為50%左右,遠低于滿足艦船安全航行的深度保證率指標要求[12],從而間接印證了非航海用DDM不能直接應用于航海上的問題。因此,分析非航海用DDM的航海安全性指標深度保證率偏低的原因,研究非航海用DDM向航海應用時的轉換方法具有現實意義。
1 不確定度擬合面的構建和模型轉換方法
1.1 基本思想
非航海用DDM向航海應用轉換方法的基本思想如下:
(1) 基于國際標準化組織制定的《測量不確定度指南》(guide of the expression of uncertainty in measurement,GUM)中推薦的不確定度合成方法,計算原始水深不確定度對非航海用DDM建模點的傳遞不確定度,采用測試點檢驗法依次計算非航海用DDM每個網格的地形描述不確定度,進而合成非航海用DDM建模點的綜合不確定度。
(2) 基于模型網格雙線性法對非航海用DDM建模點的綜合不確定度構建每個網格的不確定度擬合面,實現非航海用DDM向航海應用時的轉換。
1.2 非航海用DDM不確定度的計算
1.2.1 非航海用DDM建模點傳遞不確定度的計算
非航海用DDM采用基于距離反比加權平均法的網格建模方法,計算方法為
(1)
式中,zq為點q的內插水深值;zi為第i個點的水深值;pi為第i個點的權函數;n為參考點的個數。本文選用距離平方的倒數作為權函數,如下
(2)
將式(1)中的內插點水深值看作函數值,將參考點權函數pi中的距離di和水深值zi看作自變量。根據GUM法[13],得到參考點i的距離di和水深值zi引起內插點q的垂直標準不確定度分量為
(3)
根據GUM法,對式(3)進行整理進而得內插點q的垂直標準不確定度uDepz為
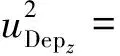
(4)
式中,uPosi、uDepi分別為參考點i的水平標準不確定度和垂直標準不確定度,進而得內插點q的垂直不確定度為
(5)
由于內插點q的平面位置已經給定,故其水平標準不確定度為0[14]。
1.2.2 非航海用DDM每個網格地形描述不確定度的計算
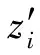
(6)
因此,非航海用DDM建模點的綜合不確定度為
(7)
1.3 不確定度擬合面的構建和模型轉化方法
2012年,國際海道測量組織在公布的《S-102水深表面產品規范》中,定義了航海表面的概念,并且指出航海表面是可以保障艦船航行安全的海洋表面,主要包括實測水深值和不確定度估值兩個方面[15]。因此,本文采用上述方法組織航海用DDM水深數據。
不確定度擬合面的構建方法如下:首先利用式(5)、式(6)分別計算非航海用DDM模型點的垂直不確定度和每個網格的地形描述不確定度,其中模型點的垂直不確定度信息標注為網格點的一個屬性值,每個網格的地形描述不確定度信息標注為該網格的一個屬性值;其次按照GUM法對每個模型網格點的垂直不確定度和相應網格的地形描述不確定度進行合成,從而得到每個模型網格點的總不確定度;最后,對于每個模型網格中的4個點的總不確定度信息,基于網格雙向性法構建非航海用DDM中每個網格不確定度擬合面。
非航海用DDM向航海應用時的轉換方法為:首先,基于網格雙線性法內插非航海用DDM中任一點的水深值z′;其次利用不確定度擬合面法計算出該點的垂直不確定度值uz;最后將z′-uz作為該點調控后的水深值應用于航海上,以實現非航海用DDM向航海應用的轉換。
2 試驗分析
2.1 試驗區域
選取3塊不同海底地形復雜程度海區的實測高密度多波束水深數據進行相關試驗,圖1為試驗海區的三維示意圖,區域大小均為1.0 km×1.0 km。其中,圖1(a) 是海底地形復雜程度為平坦的試驗海區,原始水深數據為14 569個,模型檢查點數為1127個,水深變化范圍為40.1~68.0 m,平均水深為49.7 m;圖1(b)是海底地形復雜程度為混合的試驗海區,原始水深數據為16 133個,模型檢查點數為1241個,水深變化范圍為59.3~90.2 m,平均水深為73.3 m;圖1(c)是海底地形復雜程度為復雜的試驗海區,原始水深數據為13 564個,模型檢查點數為1044個,水深變化范圍為68.4~98.9 m,平均水深為82.2 m。
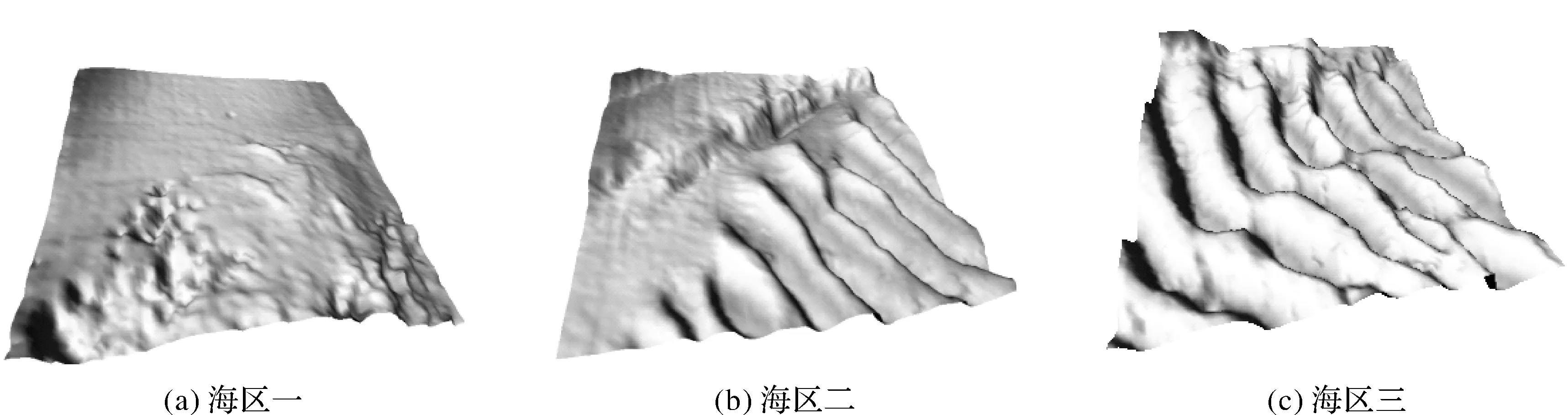
圖1 試驗海區三維示意圖
2.2 顧及不確定度擬合面的非航海用DDM深度保證率比對分析
為了驗證所提方法,以上述3塊試驗海區為例進行試驗,分別構建不同網格尺度下的非航海用DDM,并且計算非航海用DDM轉換前后的深度保證率,試驗結果見表1。
從表1可以看出,在相同網格尺度條件下,與未顧及不確定度擬合面法的非航海用DDM相比,顧及不確定度擬合面的非航海用DDM的深度保證率有了明顯的提高。這是由于顧及不確定度擬合面的非航海用DDM充分考慮了原始水深數據不確定度信息對模型點垂直不確定度的傳遞影響和模型網格的地形描述不確定度對模型不確定度的影響。
從表1中還可以發現,在相同網格尺度條件下,隨著海底地形復雜程度的不斷增大,與未顧及不確定度擬合面的非航海用DDM相比,顧及不確定度擬合面的非航海用DDM的深度保證率提高的數值也不斷增加,因為隨著地形復雜程度的不斷增大,模型網格區域的地形描述不確定度值也隨著不斷增大,進而引起顧及不確定度擬合面的非航海用DDM在表達實際水深值上的變淺量增加,從而引起模型深度保證率增大,而未顧及不確定度擬合面的非航海用DDM深度保證率則未有明顯變化,因此,非航海用DDM深度保證率提高的數值也隨著不斷增大。從表1中還可以得出,對于復雜海底地形,在大網格尺度下,顧及不確定度擬合面的非航海用DDM能夠滿足艦船航海安全需求。
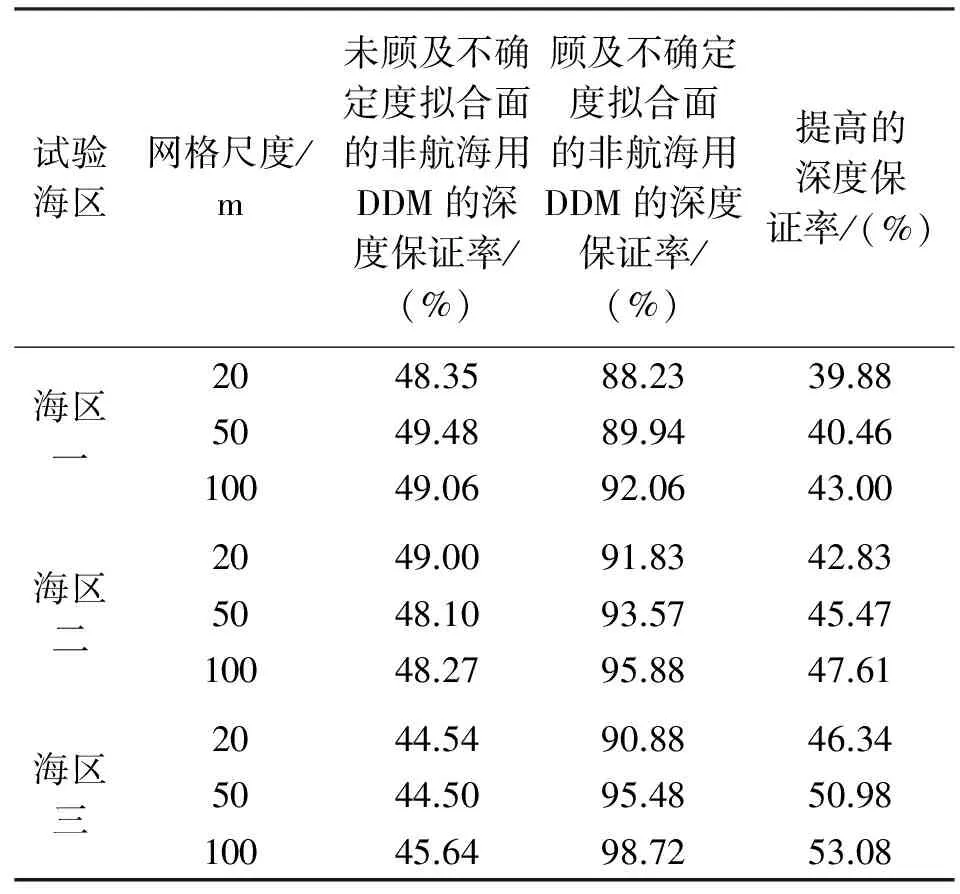
表1 非航海用DDM深度保證率統計結果
2.3 航海用DDM與非航海用DDM轉換后的模型深度保證率比對分析
為了進一步驗證所提方法的有效性,對試驗海區的多波束原始水深數據分別構建航海用DDM和非航海用DDM,并計算DDM的深度保證率。試驗結果見表2。
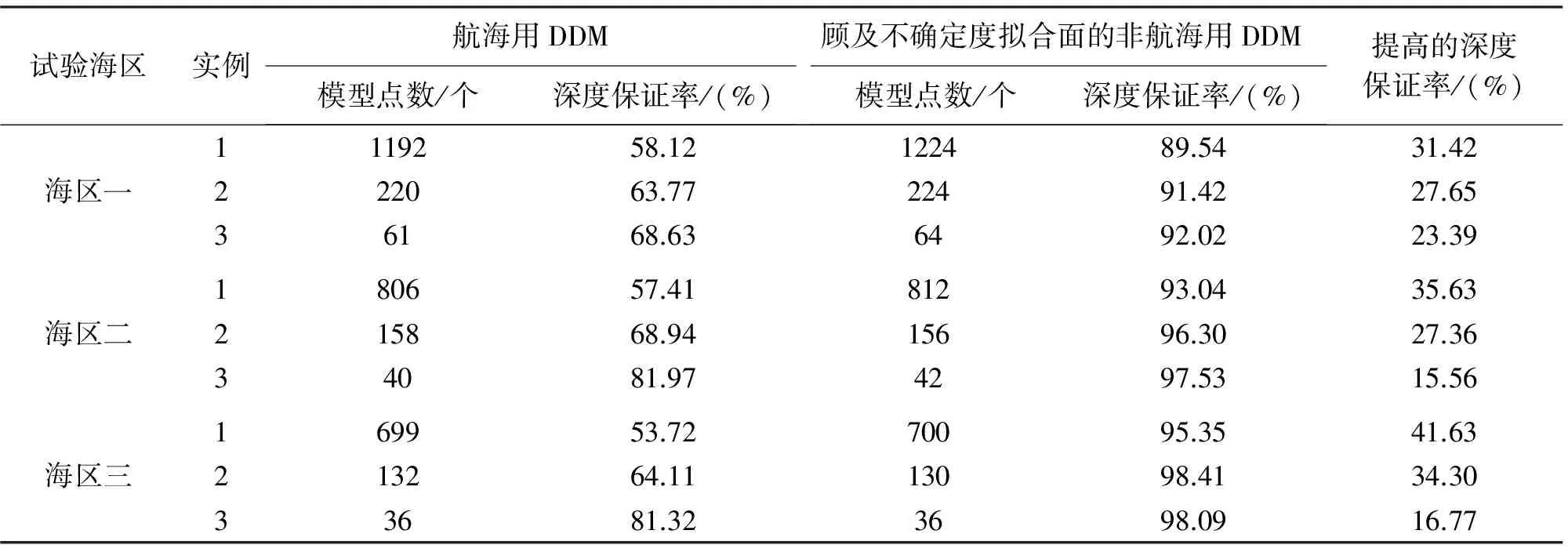
表2 DDM深度保證率統計結果
從表2可以看出,與航海用DDM相比,顧及不確定度擬合面的非航海用DDM深度保證率有了明顯提高,即顧及不確定度擬合面的非航海用DDM在應用于艦船航海時,在航海安全性上大于目前所用的航海用DDM。這是由于顧及不確定度擬合面的非航海用DDM考慮了模型點上水深不確定度和地形描述不確定度對模型深度保證率的影響所引起的。
從表2還可以看出,在同一試驗海區中,隨著建模點數的減少,與航海用DDM相比,顧及不確定度擬合面的非航海用DDM所提高的深度保證率數值在不斷減少。這是由于隨著建模點數的減少,考慮到航海用DDM采用的是取淺舍深后水深數據,所構建的模型表面將會在水深以淺的方向上出現系統性的偏差,從而提高了航海用DDM的深度保證率;而隨著建模點數的減少,顧及不確定度擬合面的非航海用DDM則主要是受到模型網格尺度變化引起的地形描述不確定度的影響,雖然地形描述不確定度會不斷增大,引起顧及不確定度擬合面的非航海用DDM所表達的模型表面變淺,但這種變淺的增量相對小于航海用DDM的變淺增量,因此,將會導致非航海用DDM深度保證率提高的數值在不斷減小。
3 結 論
本文提出了一種基于不確定度擬合面的非航海用DDM向航海應用轉換時的方法,經試驗驗證分析,得出如下結論:
(1) 與非航海用DDM相比,所提方法考慮了模型點的不確定度和模型網格的地形描述不確定度的影響,能夠明顯地提高轉化后非航海用DDM的深度保證率;在同網格尺度條件下,隨著海底地形復雜程度的不斷增大,顧及不確定度擬合面的非航海用DDM所提高的深度保證率數值也隨之不斷增大。
(2) 與航海用DDM相比,在相同建模點條件下,顧及不確定度擬合面的非航海用DDM深度保證率也有明顯提高;在同一試驗海區中,隨著建模點數的減少,顧及不確定度擬合面的非航海用DDM所提高的深度保證率數值隨之不斷減小。
本文僅從不確定度擬合面分析驗證了非航海用DDM向航海應用時的轉換方法,而針對海底地形復雜程度對模型水深不確定度信息的影響變化規律,進而影響非航海用DDM的深度保證率,還有待于進一步研究。
[1] International Hydrographic Organization. Bathymetric Surface Product Specification (Edition 1.0.0) [S]. Monaco: [s.n.], 2012.
[2] 陳長波, 劉小丁, 朱紫陽,等. 單波束測深數據的插值精度分析[J]. 測繪通報,2017(3):67-70.
[3] ANDY H, KAREN C. Harmonizing Survey Deliverables-Emerging Standards and Smart Data Exchange[C] ∥Hydro 14 22nd Conference of the International Federation of Hydrographic Societies. Aberdeen: [s.n.], 2014.
[4] 張立華, 賈帥東, 王濤,等. 深度保證率和表達度指標的定義及評估方法[J]. 武漢大學學報(信息科學版),2015, 40(5):695-700.
[5] 周慶沖. 基于航行需求的海圖制圖綜合[J]. 測繪通報,2011(9):56-58.
[6] 王春, 劉學軍, 湯國安,等. 格網DEM地形模擬的形態保真度研究[J]. 武漢大學學報(信息科學版),2009,34(2):146-149.
[7] 董箭, 彭認燦, 張立華,等. 顧及“保真性”原則的雙向滾動球變換DDM多尺度表達算法[J]. 測繪學報,2017, 46(6):789-801.
[8] 張立華, 賈帥東, 吳超,等. 顧及不確定度的數字水深模型內插方法[J]. 測繪學報,2011,40(3):359-365.
[9] 曹鴻博, 張立華, 王新成,等. 航海與非航海DDM之間的差異性分析[C] ∥全國第二十八屆海洋測繪綜合性學術研討會論文集. 西安:中國測繪地理信息學會海洋測繪專業委員會,2016:202-205.
[10] SMITH S. The Navigation Surface: a Multipurpose Bathy-metric Database[D]. New Hampshire: University of New Hampshire, 2003.
[11] 胡海, 游漣, 胡鵬,等.數字高程模型內插方法的分析和選擇[J]. 武漢大學學報(信息科學版),2011,36(1):82-85.
[12] 賈帥東. 航海DDM的構建理論與方法[D]. 大連: 海軍大連艦艇學院, 2015.
[13] BIPM, IEC, IFCC, et al. Guide of the Expression of Uncertainty in Measurement [S]. Switzerland: ISO, 1995.
[14] CALDER B. Automatic Statistical Processing of Multibeam Echosounder Data[J]. International Hydrographic review,2003,4(1):53-68.
[15] 張岳, 張大萍. 水深表面產品規范 S-102分析[J]. 海洋測繪,2014,34(1):80-83.

