GNSS自動化監測系統的大壩變形預測方法研究

黃 凱，陳渠森，鞠博曉

(1. 武漢大學衛星導航定位技術研究中心，湖北 武漢 430079； 2. 武漢大學測繪學院，湖北 武漢 430079)

全球導航衛星系統(global navigation satellite system，GNSS)定位技術近年來以其全天候、高精度、自動化等優點，在高精度大壩變形監測領域得以廣泛應用。由于大壩變形具有連續、緩慢、量級小等特點，一般在大壩關鍵結構上布設固定連續的靜態GNSS監測陣列，采取幾十分鐘到數小時時段的靜態解算進行數據處理[1]。自動化的GNSS監測系統為大壩運行狀態監測、變形規律研究提供了大樣本、高采樣率、連續的大壩變形資料，對其進行合理的分析，建立科學的變形分析與預報模型，對大壩安全運營具有重要意義。

目前，大壩變形預報一般考慮水位、溫度、時效等因素，建立統計模型、確定性模型和混合模型。然而，GNSS自動化監測數據具有大樣本、高采樣率的特點，常用的有限元單元法存在參數確定困難，計算復雜等問題；灰色理論、支持向量機法在小樣本的變形預測中效果良好，但不適用于大樣本情境；多元回歸分析等方法也無法準確表達大壩變形與環境量間復雜的非線性關系；利用自身過去到現在的大壩變形觀測值建立的自回歸模型，由于隨機因素的影響，也存在外延預報時間短、精度低等缺陷[2-7]。

針對上述難題，本文提出了一種結合小波分析與BP、NAR神經網絡預測大壩變形的新方法。該方法利用了長時間連續的GNSS變形監測資料中蘊含的長期非線性趨勢與不同尺度的周期波動特征，充分挖掘了大壩變形中隱藏的內在規律，經實例分析，與單一BP神經網絡、NAR神經網絡方法相比，該方法預測精度更高、泛化性能好，在采用GNSS自動化監測系統的大壩變形預測中具有推廣應用價值。

1 預測原理與方法

1.1 BP神經網絡基本原理

BP(back propagation)神經網絡是一種按誤差反向傳播算法訓練的多層前饋神經網絡。它具有極強的非線性映射能力。理論上，一個3層或3層以上的BP神經網絡能夠以任意精度逼近一個非線性函數，是目前應用最廣泛的神經網絡模型之一[8]。

已有研究表明，標準的BP算法存在著易陷入局部極值、收斂速度慢、過度訓練等問題[9]。為了提升網絡的泛化能力和訓練性能，本文采用貝葉斯正則化算法作為神經網絡的訓練函數。BP神經網絡一般采用均方誤差(MSE)作為網絡性能函數，而采用正則化算法將網絡性能函數修正為

F=βED+αEW

(1)

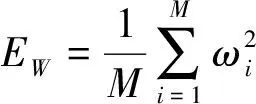
一般的正則化算法難以確定α和β的大小，當α≤β時，訓練算法盡可能減小網絡誤差，容易導致過擬合；當α≥β時，訓練算法盡可能減少有效的網絡參數，提升網絡泛化性能，容易導致欠擬合。貝葉斯正則化算法將神經網絡連接權值視為隨機變量，認為訓練集和網絡連接權集的先驗概率服從高斯分布，依據貝葉斯準則，由后驗概率最大化求解目標函數E的α和β值，從而在網絡訓練過程中自適應地調整α和β的大小，在確保網絡誤差平方和最小的前提下，有效控制網絡規模復雜度，從而顯著提高BP神經網絡的泛化能力[10]。

1.2 NAR神經網絡基本原理

NAR(nonlinear autoregressive)神經網絡屬于動態神經網絡,NAR神經網絡定義為[11-12]

y(t)=f(y(t-1),y(t-2),…,y(t-d))

(2)

式中，y(t)為當前時刻輸出值；y(t-1),y(t-2),…,y(t-d)為歷史時刻輸出值；d為延遲階數。

NAR神經網絡由輸出層、隱層、輸出層及輸入延遲階數組成。其神經網絡結構如圖1所示。

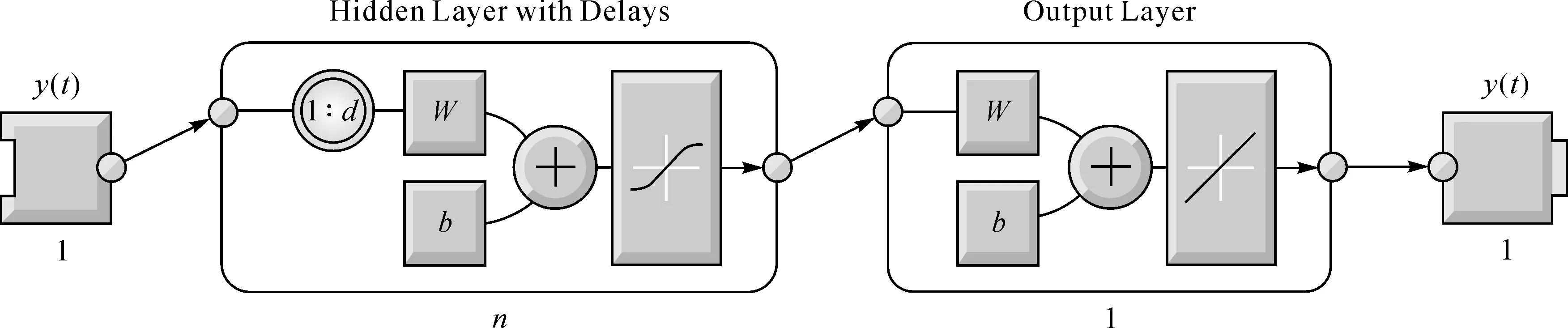
圖1 NAR神經網絡結構

圖中，y(t)表示神經網絡的輸出；d為延遲階數；n為隱層神經元個數；W為權值；b為閾值。

NAR神經網絡基于自回歸原理，利用前期若干時刻的自身歷史值來推斷當前時刻的輸出值。相比于靜態多層前饋型網絡，NAR神經網絡具備反饋和記憶功能。在網絡學習訓練過程中采用串聯模式(Openloop)，網絡轉變為靜態的前向神經網絡，用真實的輸出代替預測反饋值進行網絡訓練。預測過程中采用并聯模式(Closeloop)，每一次預測的輸出反饋到輸入端，作為下一次輸出的調整參數，完成對神經網絡的調整，循環使用多次一步向前預測，實現NAR神經網絡的多步預測。為了提升神經網絡的泛化能力，本文采用貝葉斯正則化算法作為NAR神經網絡訓練函數。

1.3 基于多尺度小波分析與BP、NAR神經網絡的預測模型

GNSS大壩變形數據序列具有較明顯的多尺度特征，利用多尺度的小波分析可將大壩變形序列分解為不同尺度的低頻信號和高頻信號[13-14]。設GNSS大壩變形序列為X(t)，對該序列進行小波分解，假設分解級數為j，可得到位移序列從低頻到高頻不同尺度的信息。再對分解后的各分量序列分別進行小波重構，得到

(3)

式中，Aj(t)為近似序列；Di(t),i=1,2，…,j為不同尺度下的細節序列。

基于BP神經網絡優秀的非線性映射能力，采用BP神經網絡擬合低頻近似序列，并預測其長期變形趨勢；采用NAR神經網絡對不同尺度下的高頻細節序列進行建模，預測其不同尺度的周期性波動。疊加各尺度下預測結果，獲得大壩變形預測值。預測模型結構如圖2所示。

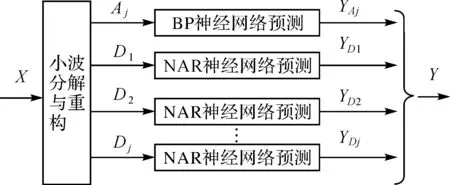
圖2 預測模型結構

2 工程實例分析

本文以西龍池上水庫GNSS大壩變形監測系統為例，選取水庫主壩體L022號GNSS監測點與壩軸線垂直的水平方向變形觀測序列進行建模，監測時間從2012年3月到2014年2月底，數據解算時段為4 h，共4380期數據，預測未來15 d(共90期)變形數據，并與實測數據進行比較來驗證本文預測模型的有效性及精度。

受極端天氣、設備故障等因素影響，變形監測數據一般存在缺失值。由于大壩變形序列非線性特征明顯，當連續缺失值數量較多，傳統的曲線擬合法插值效果差。本文采用BP神經網絡擬合大壩變形時間序列，利用缺失數據時間段的神經網絡預測值完成非線性插值。經過預處理后，對大壩變形序列進行小波信號分解，小波的分解級數應根據具體情況恰當選擇。本文經過實驗比較后，選擇采用sym8小波對大壩變形序列進行6層分解，分解后的各個分量如圖3所示。

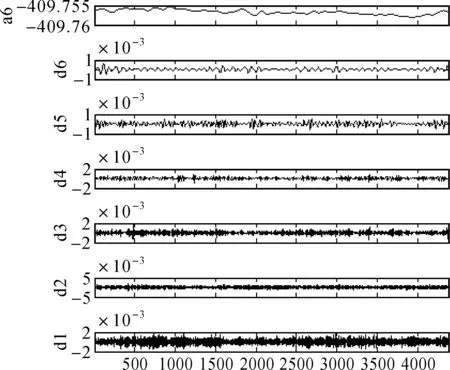
圖3 原始觀測序列及各個分解分量

由圖3可看出，低頻近似序列a6整體較為穩定，為了研究近似序列的非線性變化特征，本文采用BP神經網絡擬合該序列，經試驗比較分析，神經網絡設計為雙隱層，每層10個神經網絡元；不同尺度下的高頻細節序列存在明顯周期性波動，長時間的連續觀測序列為研究不同尺度下周期性波動特性提供了豐富的研究資料，故本文采用NAR動態神經網絡對各尺度下的細節序列進行建模，經試驗比較分析，神經網絡的延遲階數定為24，神經網絡設計為雙隱層，每層5個神經網絡元。為了降低建模誤差，神經網絡訓練前，將各分量數據歸一到[-1,1]區間，預測后反歸一化為真實預測值。各分量預測結果如圖4所示。

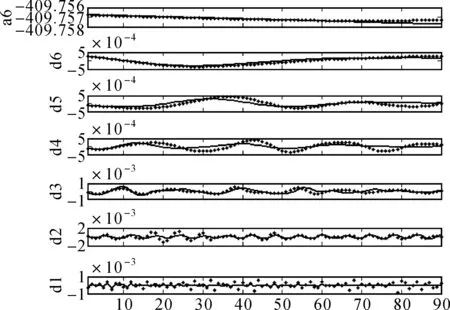
圖4 各分量預測值(實線：預測值；點：實測值)

由圖4可看出，近似序列a6的BP神經網絡預測效果較好，并預測誤差隨預測時間逐漸增大。不同尺度下各細節序列的預測效果受神經網絡訓練樣本的規律性與預測時段外部因素變化共同影響，d6、d5、d4序列的NAR神經網絡預測誤差隨時間逐漸增大，d3、d2中期預測誤差增大后，整體預測效果仍然不錯。由于GNSS大壩變形序列受明顯的周日信號影響，量級約1 mm。該信號受GNSS衛星星座幾何分布、多路徑效應、基準站觀測墩熱脹冷縮等多種因素影響，規律復雜，故d1序列在初始的幾期預測精度較高，之后迅速下降。

為了評價本文預測方法的整體預測效果，分別選用單一BP神經網絡擬合、單一NAR神經網絡與本文預測模型的預測結果進行比較，評價指標采用均方根誤差(RMSE)和平均絕對誤差(MAE)。不同預測方法的預測結果見表1。

由表1可以看出，本文提出的預測方法在不同預測期數下的預測精度都明顯高于單一BP神經網絡和NAR神經網絡模型。

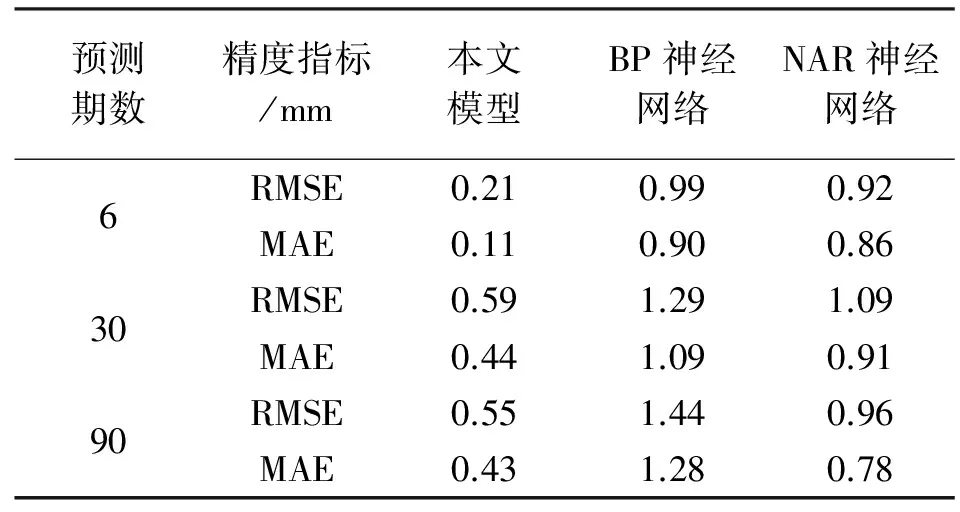
表1 不同預測方法的預測結果

工程實例表明，在高采樣率的觀測下，大壩變形受諸多因素影響，成因復雜，難以摸清規律。然而GNSS自動化監測系統長時間、大樣本的歷史觀測數據為探究大壩變形內在規律提供了突破口。通過多尺度的小波分析可分離出大壩變形中的長期非線性變化趨勢與不同尺度的復雜周期波動特征；利用BP神經網絡對反映長期變化趨勢的低頻近似序列的建模分析，可有效預測變形的整體趨勢；利用NAR動態神經網絡對反映周期性波動特征的不同尺度的細節序列建模分析，可有效預測變形中規律的周期性波動趨勢。通過試驗對比分析，與采用BP神經網絡對整體變形序列建模分析和采用NAR動態神經網絡對序列自回歸特征建模分析相比，本文預測方法兼顧了長期的歷史數據內在規律挖掘與短期的隨機擾動影響，取得了更加優越的預測效果。

3 結 語

隨著GNSS自動化監測系統在大壩、滑坡、橋梁等領域的廣泛應用，基于大數據的分析工作也日益受到關注。本文針對采用GNSS自動化監測系統的大壩變形預報問題，提出了一種結合小波分析與BP、NAR神經網絡預測大壩變形的新方法。經對比試驗表明，該方法具有很高的預測精度和良好的泛化能力，在采用GNSS自動化監測系統的大壩變形預測中具有推廣應用價值。

[1] 姜衛平，劉鴻飛，劉萬科,等.西龍池上水庫GPS變形監測系統研究及實現[J].武漢大學學(報信息科學版)，2012，37(8):949-952.

[2] 張貴鋼.三門峽大壩變形監測的有限元分析及預測[D].西安：長安大學，2007.

[3] 張永光，王蘭鋒，呂開云.小浪底水利樞紐大壩變形的灰色預測模型[J].測繪科學，2006，31(6):80-81.

[4] 王新洲，范千，許承權,等.基于小波變換和支持向量機的大壩變形預測[J].武漢大學學報(信息科學版)，2008，33(5):469-471.

[5] 李瀟.灰色最小二乘支持向量機在滑坡變形預測中的應用[J].測繪通報，2010(6):44-46.

[6] 覃劭峰.基于GM(1,1)-ARIMA最優組合的大壩預測模型[J].測繪通報，2014(S2):66-69.

[7] 范千,王新洲,許承權.大壩變形預測的支持向量機模型[J].測繪工程,2007,16(6):1-4.

[8] 朱大奇，史慧.人工神經網絡原理及應用[M].北京：科學出版社，2006.

[9] 陳孝趨，魯聰達，廖枝平.BP算法的改進及其在Matlab上的實現[J].控制工程，2005(S1):100-102.

[10] 李旭軍.貝葉斯正則化的BP神經網絡在經濟預測中的應用[J].科技信息(學術版)，2008(4):73-75.

[11] 岳新征，李磊民，孫飛.基于NAR動態神經網絡的石英撓性加速度表參數建模與預測[J].西南科技大學學報，2016，31(1):88-92.

[12] 葛宇生.基于NAR動態神經網絡后驗信息的概率水文預報[D].哈爾濱：東北農業大學，2016.

[13] 羅德河，鄭東健.大壩變形的小波分析與ARMA預測模型[J].水利水運工程學報，2016(3):70-75.

[14] 辛大鵬，田林亞，沈哲輝.小波分解AR-BP網絡模型在大壩垂直位移預測中的應用[J].測繪工程，2015(12):53-56.