藥品多車型配送的車輛指派與路徑優(yōu)化研究

劉閃

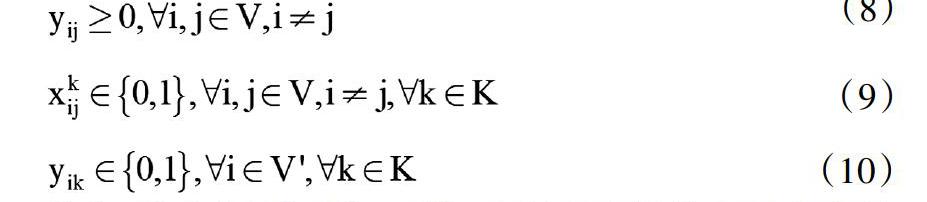
摘 要：針對(duì)醫(yī)藥產(chǎn)品所具有的體積小、重量輕、生命周期短等特點(diǎn)以及多車型配送現(xiàn)狀，文章研究帶有最后時(shí)間限制的多車型指派和配送路徑集成優(yōu)化問(wèn)題，建立了以配送成本最低為目標(biāo)函數(shù)的整數(shù)規(guī)劃模型，同時(shí)使用節(jié)約里程法進(jìn)行求解，并應(yīng)用實(shí)際數(shù)據(jù)來(lái)驗(yàn)證模型和算法的有效性。

關(guān)鍵詞：醫(yī)藥物流；多車型車輛路徑問(wèn)題；節(jié)約里程法

中圖分類號(hào)：F252 文獻(xiàn)標(biāo)志碼：A 文章編號(hào)：2095-2945（2018）35-0063-02

Abstract： According to the characteristics of pharmaceutical products such as small size， light weight， short life cycle and the current situation of multi-vehicle distribution， this paper studies the integrated optimization problem of multi-vehicle assignment and distribution path with final time constraints. The integer programming model with the lowest distribution cost as the objective function is established， and the mileage saving method is used to solve the problem， and the actual data is used to verify the validity of the model and the algorithm.

Keywords： pharmaceutical logistics； multi-vehicle routing problem； mileage saving method

1 概述

隨著我國(guó)醫(yī)藥需求量的增長(zhǎng)，醫(yī)藥物流行業(yè)面臨著前所未有的機(jī)遇與挑戰(zhàn)，配送作為醫(yī)藥物流的關(guān)鍵環(huán)節(jié)也受到愈來(lái)愈多的關(guān)注。如何設(shè)計(jì)合理的車輛調(diào)度方案和行車路線是所有醫(yī)藥物流企業(yè)所面臨的共同問(wèn)題。本文以醫(yī)藥物流企業(yè)所面臨的藥品配送成本高、效率低的問(wèn)題為研究對(duì)象，考慮到醫(yī)藥產(chǎn)品所具有的體積小、重量輕、生命周期短等特點(diǎn)以及物流企業(yè)使用多種類型車輛配送的現(xiàn)狀，通過(guò)建立數(shù)學(xué)模型來(lái)描述問(wèn)題，并用啟發(fā)式算法對(duì)其進(jìn)行求解，以期能夠降低配送成本，提高配送效率。

2 數(shù)學(xué)模型構(gòu)建

2.1 模型假設(shè)與約束條件

模型假設(shè)：（1）所有藥品均可以一起配送的；（2）配送中心及各個(gè)客戶的具體地理位置是確定的；（3）各客戶的需求是已知的；（4）配送車輛的規(guī)格是已知的；（5）忽略單行線對(duì)配送中車輛行駛的影響，即認(rèn)為所有道路都是可以往返通行的；（6）運(yùn)輸費(fèi)用和行駛里程線性相關(guān)。

約束條件：（1）同一配送路線中所需配送的藥品的總體積不得超出配送車輛的最大裝載體積；（2）每個(gè)客戶點(diǎn)所需求的藥品必須得到滿足，且由一輛車配送；（3）配送方案中使用的車輛數(shù)不得超過(guò)公司配送車輛總數(shù)目；（4）每輛外出配送的車都必須從配送中心出發(fā)，在完成任務(wù)后返回配送中心；（5）每輛配送車輛一次配送的總時(shí)間不超過(guò)額定工作時(shí)間。

其中，公式（1）為目標(biāo)函數(shù)，即所有車輛的配送成本最小。公式（2）和（3）表示每一個(gè)客戶點(diǎn)只能由一輛車來(lái)服務(wù)，并且保證車輛完成服務(wù)后離開；公式（4）是指所使用的各類型的車輛不超其可用數(shù)量；公式（5）是保證每個(gè)客戶點(diǎn)的需求都得到滿足，每個(gè)客戶點(diǎn)都被服務(wù)；公式（6）和（7）是為了保證不違反車輛容量與配送時(shí)間約束；公式（8）-（10）定義了決策變量的取值。

3 求解方法

車輛路徑問(wèn)題作為一個(gè)NP難題，會(huì)因客戶點(diǎn)數(shù)量的增加而產(chǎn)生大量的可選擇方案，難以用精確算法進(jìn)行求解，啟發(fā)式算法是解決實(shí)際問(wèn)題的常用算法。節(jié)約里程法屬于逐次逼近法，計(jì)算步驟簡(jiǎn)單，能夠在短時(shí)間內(nèi)得到計(jì)算結(jié)果，且易于考慮各種實(shí)際問(wèn)題，具有較好的擴(kuò)充性。考慮到節(jié)約里程法這一特點(diǎn)，確定用其對(duì)模型求解，具體步驟如下：

步驟1初始化基本輸入數(shù)據(jù)，如客戶位置、需求，車輛容積、成本等。

步驟2將公司的任意兩個(gè)客戶點(diǎn)i和j連接在一起，利用公式Sij=d0i+d0j-dij，計(jì)算節(jié)約值，得出節(jié)約里程集合S={s（i，j）|s（i，j）>0}，并按照降序?qū)蟂中的元素進(jìn)行排序。

步驟3若S=Φ，則算法結(jié)束，否則依次查看集合S中的第一個(gè)客戶點(diǎn)是否滿足以下三個(gè)條件之一，若滿足其中之一則轉(zhuǎn)到步驟4，否則轉(zhuǎn)到步驟8。

（1）顧客點(diǎn)i和j都不在已確定的路線上。

（2）顧客點(diǎn)i和j有一個(gè)在已確定的路線上，一個(gè)不在已確定路線上，在已確定路線上的客戶點(diǎn)是該線路的起點(diǎn)或終點(diǎn)。

（3）客戶點(diǎn)i和j屬于已確定的不同路線，并且一個(gè)是線路中的第一個(gè)顧客點(diǎn)，另一個(gè)是線路中的最后一個(gè)顧客點(diǎn)。

步驟4計(jì)算連接客戶點(diǎn)i和j之后，判斷配送時(shí)間是否滿足約束條件，若滿足則轉(zhuǎn)到步驟5；否則轉(zhuǎn)到步驟8。

步驟5考察安排客戶點(diǎn)i和j 之后，線路上的配送車輛會(huì)不會(huì)超出載容量，若vij？燮Vk，則轉(zhuǎn)到步驟6，否則跳轉(zhuǎn)到步驟8。

步驟6把客戶點(diǎn)i和j安排到同一路線上。

步驟7將含有客戶點(diǎn)i和j的集合中的元素刪除。

步驟8若所有客戶點(diǎn)對(duì)都被考察，則轉(zhuǎn)至步驟9，否則轉(zhuǎn)至步驟3。

步驟9為該路徑安排容積最接近其貨物總量的車輛，更新可用車輛的信息。

步驟10若集合S為空集，則算法結(jié)束，否則跳轉(zhuǎn)至步驟3。

步驟11查看是否有遺留的客戶未被安排到路徑中，若有，則為其安排路徑，否則，結(jié)束算法。

4 模型求解結(jié)果分析

4.1 測(cè)試算例

為驗(yàn)證模型及算法的有效性，使用真實(shí)案例中的數(shù)據(jù)來(lái)進(jìn)行仿真實(shí)驗(yàn)。算例中的車輛信息如表1所示，算例中的客戶數(shù)量為90個(gè)，本實(shí)驗(yàn)在matlab R2016b平臺(tái)下進(jìn)行，實(shí)驗(yàn)所用計(jì)算機(jī)參數(shù)配置為Intel CoreTMi5-8250U CPU @ 1.60GHz 1.80GHz。

4.2 結(jié)果分析

對(duì)本文所提出算法的驗(yàn)證和評(píng)價(jià)是將算法所得方案與原始方案進(jìn)行比較，評(píng)價(jià)指標(biāo)為：配送所用車輛數(shù)，平均裝載率和總配送成本。

經(jīng)過(guò)10次仿真實(shí)驗(yàn)，將實(shí)驗(yàn)結(jié)果匯總在表2，分析發(fā)現(xiàn)，算法所得最優(yōu)方案中的配送所用車輛數(shù)從8輛減少為6輛，車輛裝載率從53.9%提高到84.37%，提高了30.47%，總配送成本由3375.5降低為2245.71，減少了1129.79，且10次實(shí)驗(yàn)的平均解與原始方案相比也有明顯的優(yōu)化效果，裝載率平均提高29.85%，總配送成本平均減少1116.13，說(shuō)明算法具有穩(wěn)定性和有效性。

5 結(jié)束語(yǔ)

本文針對(duì)醫(yī)藥產(chǎn)品的配送問(wèn)題，建立了以包括車輛的固定使用成本和基于里程的變動(dòng)成本在內(nèi)的總配送成本最小化為目標(biāo)，同時(shí)求解車輛指派方案和車輛行駛路徑方案的數(shù)學(xué)模型，并使用節(jié)約里程法對(duì)該模型進(jìn)行求解，最后以醫(yī)藥物流公司的實(shí)際情況為案例，對(duì)其配送方案進(jìn)行優(yōu)化。通過(guò)大量的仿真實(shí)驗(yàn)，證明了所提出模型和算法的可行性和現(xiàn)實(shí)有效性。

參考文獻(xiàn)：

[1]Clarke G， Wright J W. Scheduling of Vehicles from a Central Depot to a Number of Delivery Points[J]. Operations Research， 1964，12（4）：568-581.

[2]葛顯龍，許茂增，王偉鑫.多車型車輛路徑問(wèn)題的量子遺傳算法研究[J].中國(guó)管理科學(xué)，2013，21（01）：125-133.

[3]張錦，謝克明.蟻群算法在醫(yī)藥物品配送路徑優(yōu)化中的應(yīng)用[J].太原理工大學(xué)學(xué)報(bào)，2009，40（6）：600-603.