k0固結飽和黏土的動剪切模量與阻尼比試驗研究

楊騰 ，王建華 *，姚海慧

（1.天津大學水利工程仿真與安全國家重點實驗室，天津 300072；2.天津大學巖土工程研究所，天津 300072）

0 引言

等效線性方法在場地動力穩定性評價與分析中較為常用。該方法的應用需要通過試驗確定土的動剪模量與剪應變（G-γ）以及阻尼比與剪應變（λ-γ）之間的關系。飽和黏土是海洋地基淺層范圍內經常遇到的典型土層，國內外學者對飽和黏土的G-γ和λ-γ關系進行了大量的研究，主要考慮了黏土自身性質及試驗條件的影響，包括顆粒級配、含水量、塑性指數、圍壓、固結比、加載頻率以及試驗儀器種類等[1-2]。當進行場地動力特性評價時，應根據真實工況和土層的勘測資料綜合考慮選擇主要因素，研究其對G-γ和λ-γ關系的影響。

已有研究多數在均等固結壓力條件下進行[3]，而海底土層在漫長地質年代中常處于k0固結狀態，通過等壓或偏壓固結試驗無法真實反映海底土層的初始應力條件。此外，海洋平臺地基土常承受上部結構重力而產生豎向附加偏應力[4]，而且在波浪等循環荷載的長期作用下，產生的超孔隙水壓力和應變的累積也將對動剪模量和阻尼比產生影響[5-6]，因此有必要研究k0固結條件下飽和黏土在循環應力作用下G-γ以及λ-γ之間的關系，并考慮附加偏應力和循環應力歷史的影響。

綜上，本文開展了一系列k0固結飽和黏土的動三軸試驗，研究了圍壓、初始靜偏應力、加載歷史3種因素對動剪模量-動應變和阻尼比-動應變關系曲線的影響。

1 試驗內容和方法

1.1 試驗土樣與儀器

試驗用土選用天津渤海海灣灘海地區的軟土制備的重塑土，重塑過程先將土烘干、粉碎、制成泥漿，然后堆載預壓，制得黏土含水率在38%左右，液限為43.1%，塑限為21%，塑性指數為22.1，重度為18.5 kN/m3，采用旋轉切削法制備三軸試驗土樣，最終試樣直徑3.91 cm，高度為8 cm。

試驗采用HX-100多功能電氣伺服控制動靜三軸儀。采用應力控制加載方式，應力波形為正弦波，頻率為0.1 Hz。微機控制軟件可設定波形和應力幅值，并自動采集荷載、位移等數據。

1.2 試驗方法

試樣在三軸壓力室內進行反壓飽和，孔隙水壓力系數B值均達到98%以上。先施加側向壓力至預定值，固結的同時逐級施加軸向應力，保持三軸試樣無側向變形。k0固結完成后，開展不排水靜力三軸壓縮試驗（CU），獲得不同圍壓時黏土的三軸壓縮強度qf，然后按不同初始偏應力比qa/qf和循環應力比qcy/qf組合開展不排水循環三軸試驗。由于先期較小應變幅值的累積應變對后繼大應變幅值滯回圈形狀基本沒有影響[7]，可采取逐級施加動應力的方法，得到G-γ與λ-γ關系曲線。試驗方案見表1。

考慮初始偏應力的影響時，在試樣固結完成后，在不排水條件下按一定的qa/qf值施加軸向偏應力，最后施加正弦波形的動應力。

對于循環應力加載歷史對動剪切模量和阻尼比影響的研究，和以往直接研究動模量隨應力作用次數衰減的方法不同，本文通過動三軸研究了累積應變εp對G-γ與λ-γ曲線的影響，具體步驟為：在黏土三軸試樣k0固結完成后，施加動應力使試樣達到預定累積應變εp，分別為0%、2%、3.5%、5%，然后分級施加動應力，獲得預定累積應變下G-γ與λ-γ關系曲線。

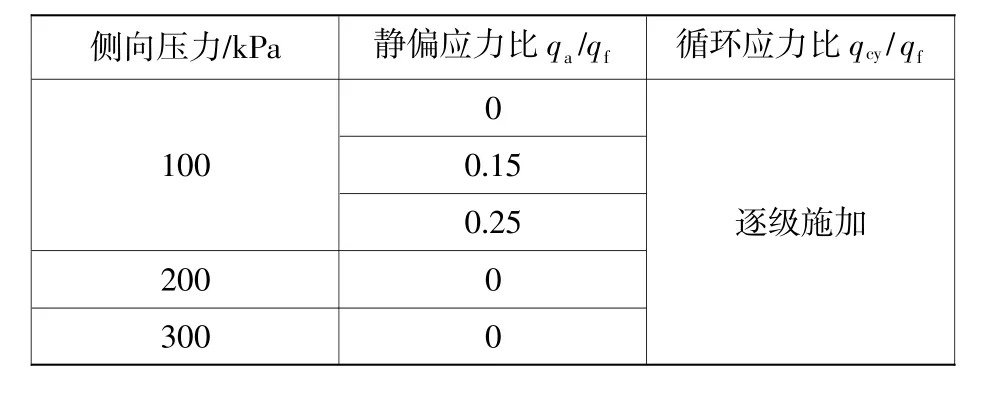
表1 試驗方案Table1 Test scheme

2 試驗結果與分析

2.1 試驗數據處理

在動三軸壓力室內對重塑黏土進行k0固結，然后在不排水情況下作用靜偏應力，土樣存在初始偏應力作用產生的初始剪應力，在循環應力作用下產生殘余累積應變，使得應力應變滯回圈不閉合。隨著應力作用次數的增加，累積應變趨于穩定，滯回圈也逐漸閉合，應力應變滯回曲線如圖1所示。但應力應變滯回圈趨于閉合需在一定動應力作用周期后，黏土試樣受循環應力歷史作用，孔壓、殘余變形均有明顯累積，對動剪切模量和阻尼比產生影響。因此，在考慮圍壓和初始偏應力等因素對G-γ與λ-γ的影響時，試驗結果就不具代表性。為了保證在相同初始狀態下研究動剪切模量和阻尼比隨動剪應變曲線變化規律，找出應力應變滯回圈不閉合時動剪切模量和阻尼比的計算方法是必要的。

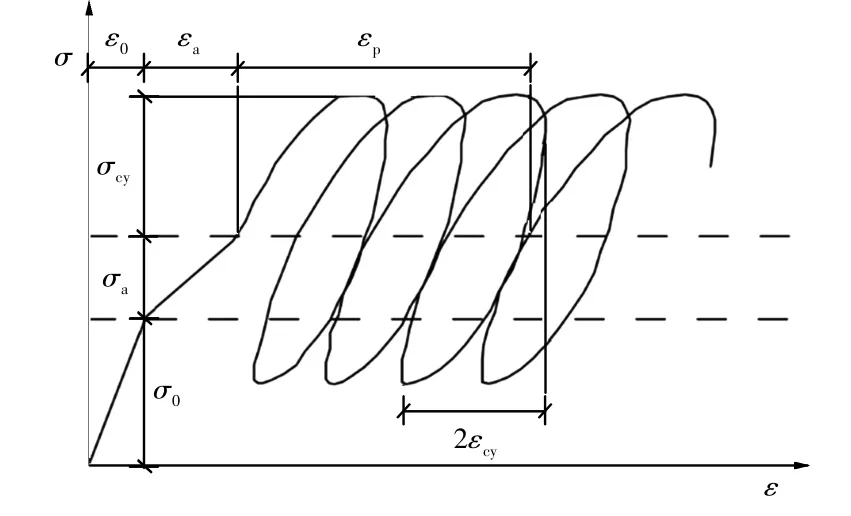
圖1 應力應變滯回曲線Fig.1 Stress-strain hysteresis curve

在非閉合滯回圈中，殘余塑性變形耗功并不造成應變對應力滯后，需要去除滯回圈中累積應變的影響。本文提出，首先計算每一循環應力作用周期的累積應變增量Δεp，對每周期采集的n個數據點按線性關系減去累積應變增量Δεp，至第n個數據點時完全減掉累積應變增量，實現應力應變滯回圈的閉合。選取某循環應力作用下第2周期采集得到的應力應變數據，按上述方法消除累積應變的影響，得到閉合的滯回圈，如圖2所示。

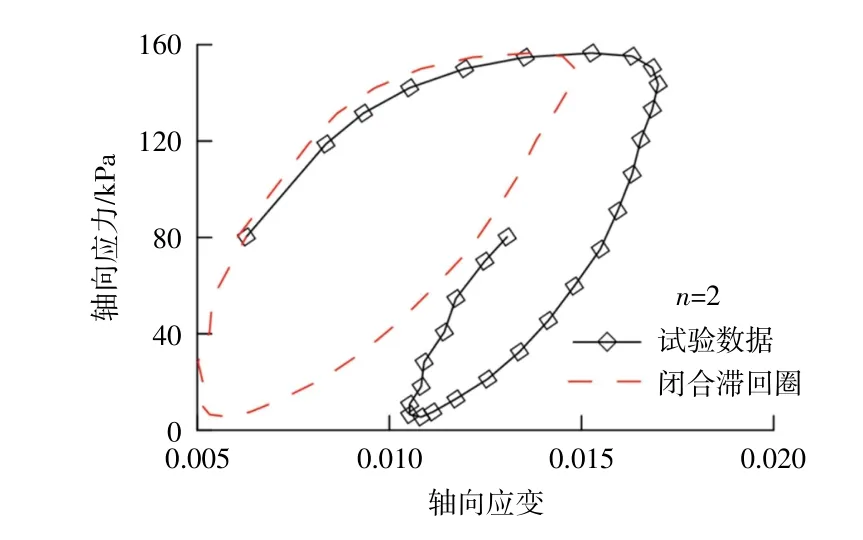
圖2 閉合應力應變滯回圈Fig.2 Closed stress-strain hysteresis loop

當應力應變滯回圈閉合時，動模量、阻尼比按式（1）、式（2）計算。

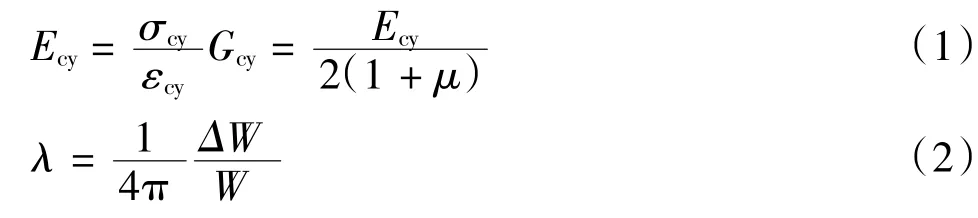
式中：σcy為循環應力幅值；εcy為循環應變幅值；μ為泊松比，由于試驗為固結不排水試驗，μ取0.5[8]；Ecy為動壓縮模量；Gcy為動剪切模量；ΔW為一個周期內損耗的能量；W為作用的總能量。

2.2 圍壓對動剪切模量的影響

開展循環三軸試驗，得到圍壓σ3為100 kPa、200 kPa、300 kPa的k0固結黏土的G-γ試驗數據，如圖3所示。本文利用Hardin-Drnevich公式[9]擬合試驗數據，如式（3）。該式參數較少，且物理意義明確，擬合結果見圖3。采用何昌榮等[10]提出的式（4）歸一化最大剪切模量Gmax隨圍壓的變化，式中引入與固結比有關的參數，克服了以平均固結有效應力為參數時不能很好反映初始固結比對最大動剪切模量影響的不足。式中：Gmax為最大動剪模量；γr為參考應變；γcy為動剪應變；Kc為固結比σ1/σ3；m、n、k1為擬合參數；Pa為大氣壓。

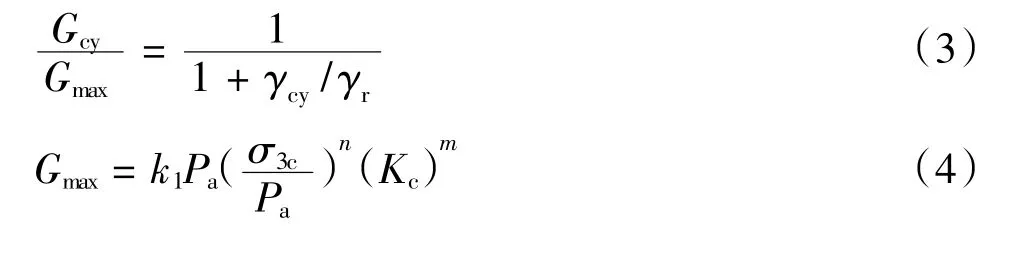
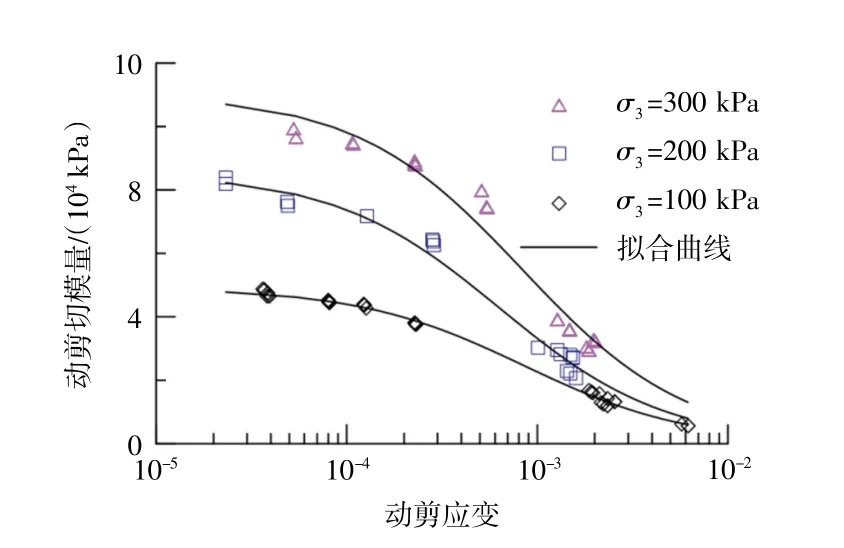
圖3 不同圍壓下模量隨動剪應變的變化Fig.3 G-γrelationship under different confining pressure

圖4 表示了最大動剪模量Gmax隨側向壓力σ3的變化，并利用式（4）擬合試驗數據，可以看出試驗結果與計算結果較為接近。利用最大動剪模量Gmax作為歸一化參數，得到不同側向壓力σ3對應的G/Gmax-γ關系曲線，如圖5所示。可以看出，不同側向壓力對應的G/Gmax-γ試驗結果均落在一條曲線附近，也就是說，k0固結黏土的G/Gmax-γ關系曲線受側向壓力影響不大。

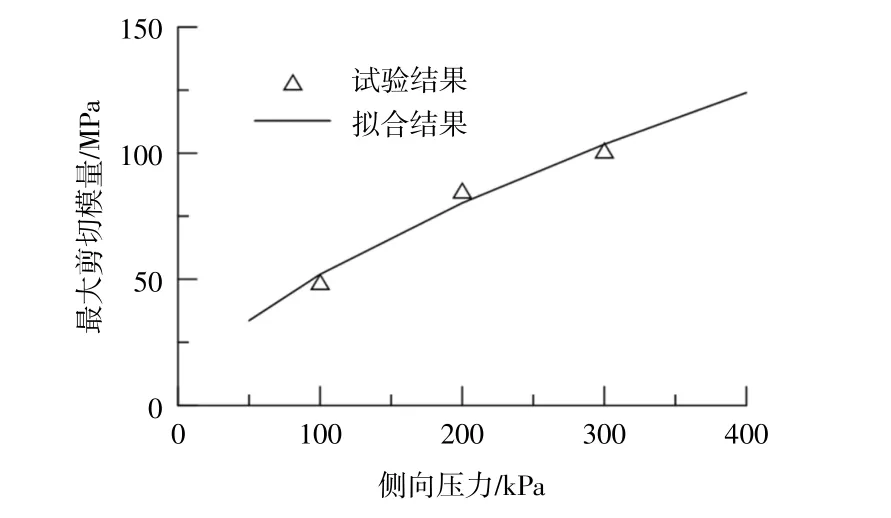
圖4 最大動剪模量擬合曲線Fig.4 The fitting curve of maximum shear modulus

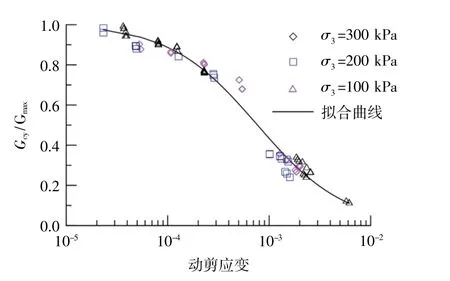
圖5 不同圍壓下動剪模量歸一化曲線Fig.5 Normalized curve of G cy/G max under different confining pressure

2.3 靜偏應力對動剪切模量與阻尼比的影響

圖6 為σ3=100 kPa時不同靜偏應力比下動剪切模量隨動剪應變變化的試驗及擬合結果，可以看出，當動應變幅值小于0.01%時，不同靜偏應力下剪切模量變化不明顯，隨著動應變幅值增加，靜偏應力的作用使得G-γ關系曲線下移。可以解釋為，對于k0固結黏土在不排水情況下施加靜偏應力時，土體內孔壓的上升降低了土體的有效應力，對G-γ曲線產生一定影響。

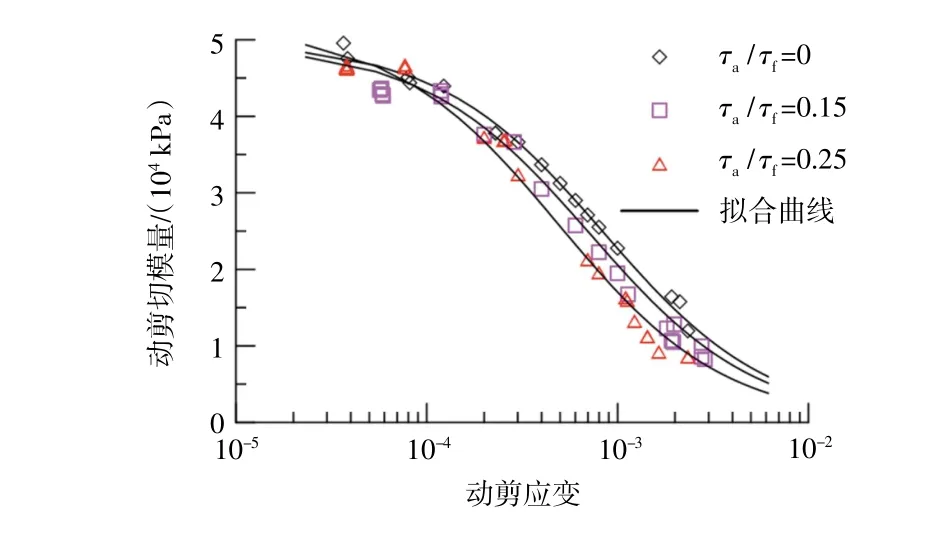
圖6 不同靜偏應力下G-γ曲線Fig.6 G-γcurvesunder different deviate stress

利用式（5）所示的指數函數擬合阻尼比隨動剪應變的變化關系：

式中：λ為阻尼比；A、b為擬合參數。

圖7為不同靜偏應力水平下阻尼比隨動剪應變變化的試驗結果及擬合曲線，可以看出，阻尼比試驗數據與動模量相比較為離散，λ-γ關系曲線變化規律與G-γ曲線相反，在靜偏應力作用下曲線有一定上移。

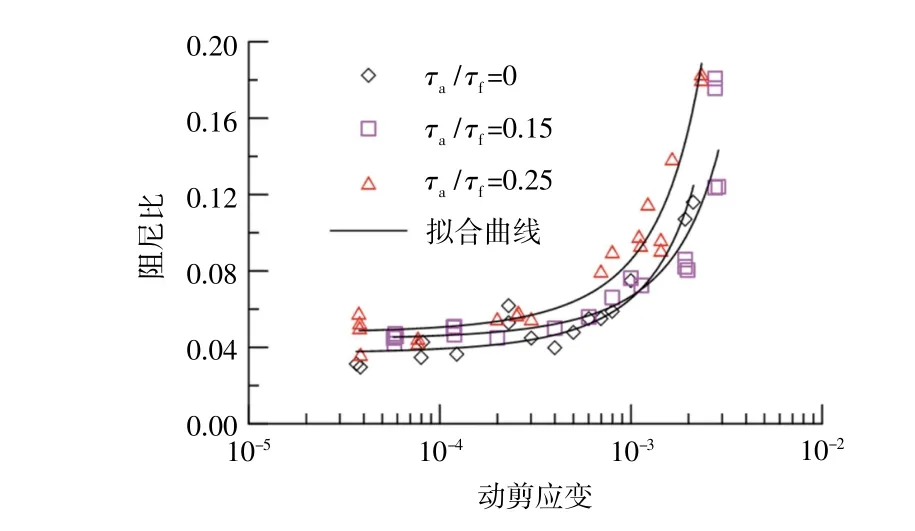
圖7 不同初始靜偏應力下λ-γ曲線Fig.7 λ-γcurvesunder different deviate stress

綜上，對于海洋平臺基礎在循環荷載下的動力穩定分析，考慮其上部結構自重在地基土層上產生的偏應力對G-γ與λ-γ關系曲線的影響是必要的。

2.4 循環荷載歷史對動剪切模量與阻尼比的影響

黏土在長期循環荷載作用下，累積應變與動模量、阻尼比的變化存在一定聯系。本文在考慮循環應力歷史影響時，以累積應變εp為度量，研究了累積應變對G-γ與λ-γ關系曲線的影響。圖8代表了黏土試樣累積應變為0%、2%、3.5%、5%時動模量隨動應變幅值的變化關系。由圖8可以看出，當動應變幅值小于0.1%時，土體的動剪切模量在相同動剪應變幅值下有顯著衰減；當動應變幅值大于0.1%時，不同累積應變后的試樣G-γ曲線無明顯區別。

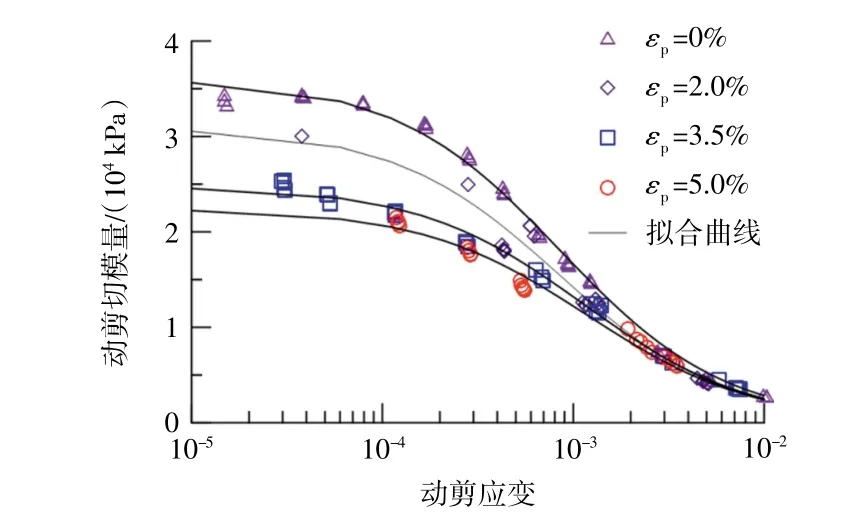
圖8 不同累積應變下G-γ曲線Fig.8 G-γcurvesunder different cumulative strain

將不同累積應變時的G-γ曲線對應的小循環應力下的動剪切模量視為初始動剪模量G′，并利用式（6）擬合G′隨累積應變的發展趨勢，結果見圖9，可以看出G′隨累積應變的增加線性減小。

式中：δ為參數；εp為累積應變。

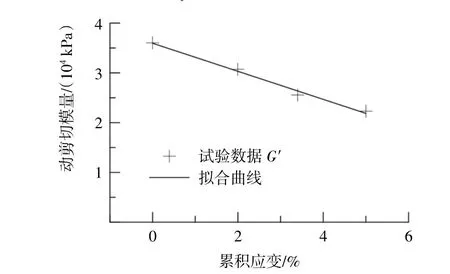
圖9 動剪切模量G′隨累積應變變化Fig.9 Variation of dynamic shear modulus G′with cumulative strain

因此，在考慮循環應力歷史對G-γ曲線影響時，當動應變幅值小于0.1%時，可將式（3）中Gmax替換為式（6）得到的G′；當動剪應變大于0.1%時，式（3）的Gmax仍然利用式（4）計算，歸一化后的動剪切模量如圖10所示。

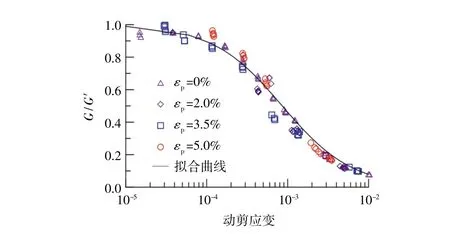
圖10 不同累積應變下G/G′-γ歸一化曲線Fig.10 Normalized curve G/G′-γ under different cumulative strain

圖11 給出了不同累積應變后的阻尼比隨動剪應變的變化曲線，可以看出阻尼比受累積應變影響不大，均落在式（5）擬合曲線附近。

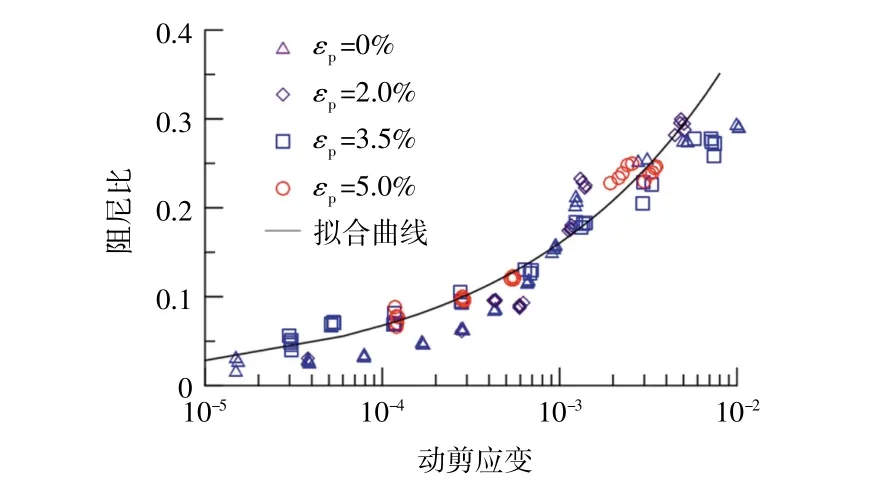
圖11 不同累積應變下λ-γ曲線Fig.11 λ-γcurvesunder different cumulative strain

3 結語

開展了一系列k0固結飽和黏土的動三軸試驗，研究了圍壓、靜偏應力、加載歷史3種因素對動剪模量-動應變（G-γ）和阻尼比-動應變（λ-γ）關系曲線的影響，得出以下結論：

1）結合Hardin-Drnevich模型和可以反映k0固結偏應力影響的最大模量計算公式擬合k0固結黏土動剪切模量隨動剪應變的變化曲線，歸一化結果表明G/Gmax-γ曲線受側向壓力影響不大。

2）G-γ關系曲線隨不排水初始靜偏應力水平的增加有一定下移，λ-γ曲線隨不排水初始靜偏應力水平的增加有一定上升，當進行動力穩定性分析時，認為考慮結構自重產生的偏應力的影響是必要的。

3）初始動剪模量G′隨累積應變增大逐漸減小，并呈現出良好的線性規律；累積應變對λ-γ關系影響不大。不同累積應變條件下的G-γ關系可用初始動剪模量G′作為歸一化參數，并具有良好的歸一化特性。

[1] PARK D.Evaluation of dynamic soil properties:strain amplitude effectson shear modulus and damping ratio[M].NewYork:Cornell University,1998.

[2] 孫靜，袁曉銘.固結比對黏性土動剪切模量影響的研究[J].巖土力學，2010，31（5）：1 457-1 462.SUN Jing,YUANXiao-ming.Effect of consolidation ratio of cohesivesoilson dynamic shear modulus[J].Rocks and soil mechanics,2010,31(5):1 457-1 462.

[3] 賀為民，李德慶，楊杰，等.土的動剪切模量、阻尼比和泊松比研究進展[J].地震工程學報，2016，38（2）：309-317.HE Wei-min,LI De-qing,YANG Jie,et al.Recent progress in researchondynamic shear modulus,dampingratio,and poisson ratio of soils[J].China Earthquake Engineering Journal,2016,38(2):309-317.

[4] 蔡袁強，王軍，徐長節.初始偏應力作用對蕭山軟黏土動彈模量與阻尼影響試驗研究[J].巖土力學，2007，28（11）：2 291-2 302.CAIYuan-qiang,WANGJun,XU Chang-jie.Experimental study ondynamic elastic modulusand dampingratioof Xiaoshan saturated soft clay considering initial deviator stress[J].Rocks and Soil Mechanics,2007,28(11):2 291-2 302.

[5] ZHOU J,GONG X.Strain degradation of saturated clay under cyclic loading[J].Canadian Geotechnical Journal,2001,38(1):208-212.

[6]SUBRAMANIAM P,BANERJEE S.Shear modulus degradation model for cohesive soils[J].Soil Dynamics and Earthquake Engineering,2013,53(10):210-216.

[7] 尚守平，劉方成，杜運興，等.應變累積對黏土動剪模量和阻尼比影響的試驗研究[J].巖土力學，2006，27（5）：683-688.SHANGShou-ping,LIUFang-cheng,DUYun-xing,et al.Experimental study on effect of shear strain accumulation on dynamic shear modulusand damping ratio of clay soil[J].Rock and Soil Mechanics,2006,27(5):683-688.

[8] 王建華，周揚銳，張群.一種測試動三軸試樣泊松比的方法[J].世界地震工程，2010（S1）：23-27.WANG Jian-hua,ZHOU Yang-rui,ZHANG Qun.Measuring method for poisson ratio of cyclic triaxial specimens[J].World Earthquake Engineering,2010(S1):23-27.

[9]HARDIN B O,DRNEVICH V P.Shear modulus and damping in soils:design equationsand curves[J].Geotechnical Special Publication,1972,98(118):667-692.

[10]何昌榮.動模量和阻尼的動三軸試驗研究[J].巖土工程學報，1997，19（2）：39-48.HEChang-rong.Dynamic triaxial test on modulus and damping[J].Chinese Journal of Geotechnical Engineering,1997,19(2):39-48.