基于ANSYS二次開發的高階連續梁數值模擬★

殷玉沉 朱彥濤 孫玉周

(1.中原工學院，河南 鄭州 450007； 2.西藏職業技術學院，西藏 拉薩 850000)

0 引言

高階連續理論能夠反映出特殊本構反應，例如在偶應力理論、應變梯度連續理論中引入尺度因子描述高階連續結構的局部彎曲效應[1-3]。在研究高階連續結構過程中，尺寸效應的影響日益被重視，但是傳統有限元法構造高階形函數需要大量的工作[4]，而且沒有引入尺度因子不易實現數值模擬。采用傳統有限元法分析計算，會遇到網格劃分困難以及近似函數不連續等問題，但應用適當的基函數和權函數，移動最小二乘法(MLS)可以比較容易地構造出高階形函數[5,6]。近年來，一些學者對相關問題進行了研究，李雷等[7]將無網格法和高階理論相結合，對巖土工程中的一些問題進行數值模擬；李莉等[8]利用虛功原理建立各向異性修正偶應力理論并引入不同的材料細觀參數,建立適用于層合板/夾層板的偶應力理論模型；孫玉周等[9，10]使用無網格法研究基于高階連續理論下的碳納米管的多尺度效應以及彎曲梁等問題。上述的研究主要集中在通過無網格法與高階理論相結合，以及考慮結構尺度效應影響等方面，但是將高階連續理論應用在有限元分析中以及將其在有限元軟件中實現數值模擬的研究較少。

ANSYS作為有限元領域的大型通用軟件，被世界各工業領域廣泛接受。為適應具體工程需求，ANSYS還提供了APDL,UPFs,UIDL(用戶界面設計語言)及TckTk(工具命令語言/圖形開發工具箱)4種二次開發工具[11]。針對本文提出的問題，由于ANSYS在網格劃分以及高階連續結構分析上存在局限性，需要對ANSYS軟件進行二次開發。本文采用移動最小二乘法可以方便的構造高階連續形函數的優點，建立高階連續梁模型，通過Fortran語言編寫用戶單元子程序，進行ANSYS的二次開發，實現高階連續梁在有限元軟件中的數值模擬，并引入尺寸因子對高階連續梁進行分析。

1 基于MLS的計算框架

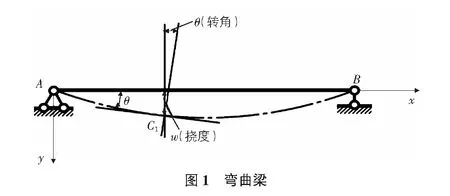
在傳統彎曲梁(如圖1所示)的基礎上，高階連續梁模型的應力和應變分別定義為：

應變：

(1)

應力：

σxx=Eεxx+lxεxxx
τxxx=g2Eεxxx+lxEεxx
τyxx=g2Eεyxx

(2)

其中,E為彈性模量；w為梁的撓度；g為體本征尺度因子；lx為面本征尺度因子。

梁在應變能及外力的作用下，根據虛功原理可得:

(3)

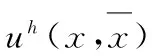
(4)

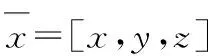
令m=4,則一維三次基函數為:

aT(x)=(1,x,x2,x3)

(5)

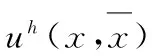
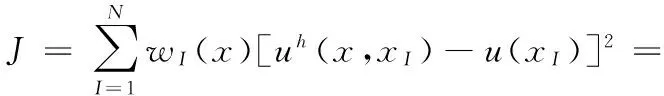
(6)

其中，wI(x)=wI(x-xI)為節點xI處的權函數，當權函數wI(x)在節點支撐域范圍內時，wI(x)>0，否則，wI(x)=0。

由式(3)得：

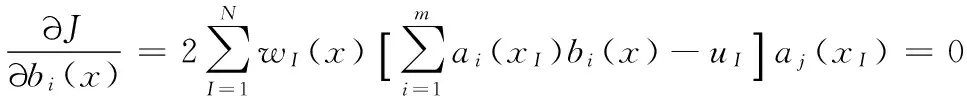
j=1,2,3,…，m

(7)

由此得:

(8)

即:

A(x)b(x)=B(x)u

(9)

令：

B(x)=[wI(x)a(xI)w2(x)a(x2)…wN(x)a(xN)]

(10)

則形函數為：

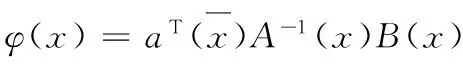
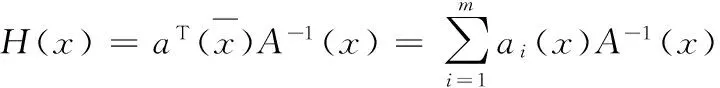
(11)

權函數ωI(x)在節點xI處的值最大，而且支撐域邊界附近趨于0，即當r=(x-xi)/dmI>1時，w(r)=0，dmI為節點支撐域的直徑。

采用三次樣條權函數，綜上可求得形函數φ(x)的導數為:

φI,x(x)=H,x(x)B(x)+H(x)B,x(x)l
φI,xx(x)=[H,xx(x)B(x)+2H,x(x)B,x(x)+H(x)B,xx(x)]l
φI,xxx(x)=[H,xxx(x)B(x)+3H,x(x)B,xx(x)+3H(x),xxB,x(x)+H(x)B,xxx(x)]l

(12)

在無網格法的計算框架下，撓度的二階和三階導數近似為:

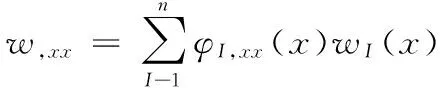
(13)

由式(12),式(13)代入式(3)可得高階連續梁的總剛度矩陣表達式：

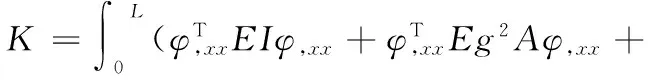
(14)

由式(14)可知，高階連續問題中出現高階位移導數，傳統有限元法處理高階形函數的工作量比較大，利用移動最小二乘近似(MLS)構造高階形函數，位移高階導數可以直接通過節點位移插值得到。

2 ANSYS二次開發

基于ANSYS為用戶提供的二次開發功能，通過UPFs的特性實現ANSYS軟件模擬一維高階連續梁。由于ANSYS中傳統彎曲梁缺少高階連續理論，下面將含有的高階項從高階連續梁中分離出來即K1。通過添加附加項K1到用戶自定義程序UELMatx.F中，實現高階連續理論在有限元軟件中的應用。

從式(14)得：

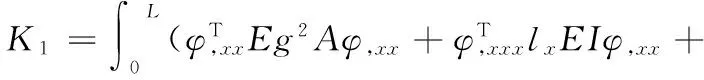
(15)

ANSYS的用戶子程序UELMatx用于訪問單元矩陣和載荷向量，主要目的是修改或監視單元剛度矩陣和荷載向量。程序編譯過程中需要解決的關鍵問題主要在以下方面：

1)ANSYS二次開發編譯鏈接環境建立；

2)利用APDL(參數化設計語言)創建節點支撐域覆蓋范圍內的單元；

3)將附加項K1通過編譯用戶自定義程序UELMatx實現與有限元軟件結合。

ANSYS源程序是基于FORTRAN語言編寫，為方便程序編譯鏈接，采用FORTRAN語言對程序進行編譯開發。本文基于ANSYS15.0進行二次開發，程序編譯鏈接過程如下:

1)將編譯完成的子程序UELMatx.F放置在ANSYS Incv150ansyscustomuserwinx64文件夾中，使用該文件夾下的ANSCUST.BAT批處理文件，編譯連接成功后生成用戶自定義ANSYS.exe文件；

2)激活UPFs：打開ANSYS15.0>Mechanical APDL Product Launcher 15.0，選擇用戶自定義生成的ANSYS.exe文件路徑，也可通過GUI操作進行。該用戶子程序在求解之前調用，調用命令如下：USRCAL,UELMATX。

3 算例分析

3.1 簡支梁的計算分析

如圖1所示，利用簡支梁的例子來驗證編譯開發的用戶子程序UELMatx在ANSYS中調用求解時的收斂性及精確度。簡支梁受集中力F=1 N作用在跨中，梁的長度為10 mm，梁截面高度h=1 mm，厚度b=0.01 mm，梁的橫截面面積A=h×b，彈性模量E=1.0×105MPa。

本文利用Beam3單元建立一維梁模型，為驗證高階連續梁在ANSYS二次開發后的數值計算精度，與基于無網格法的一維高階連續梁的數值計算結果進行對比。梁上布置不同的節點數，梁中點撓度變化見表1。

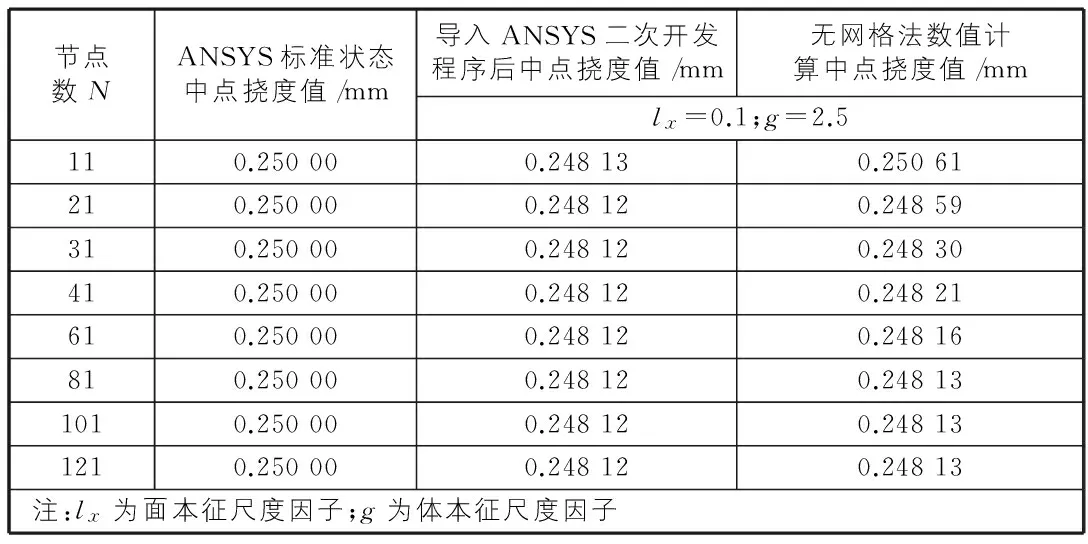
表1 不同節點數時梁中點撓度值

假設一維簡支梁的面本征尺度和體本征尺度為固定值。由表1的計算結果可以看出，不同節點數的一維高階連續簡支梁通過ANSYS二次開發模塊求解的中點撓度值收斂且基本與無網格法框架下的數值計算結果吻合。

從表1的數據可以知道高階連續理論下的簡支梁中點撓度值與ANSYS標準狀態下的結果存在極小差異。利用ANSYS二次開發后的計算模塊分析尺度因子的變化對梁的撓度影響，相關實常數不變，只改變尺寸因子的數值，計算結果分別見表2,表3。

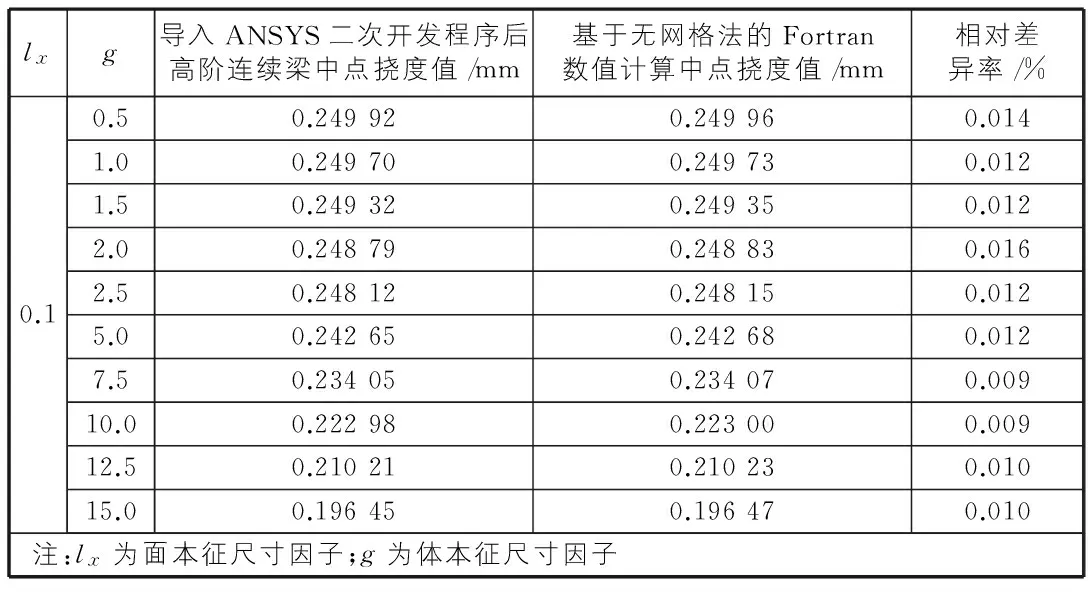
表2 尺寸因子g變化時對高階連續梁中點撓度值

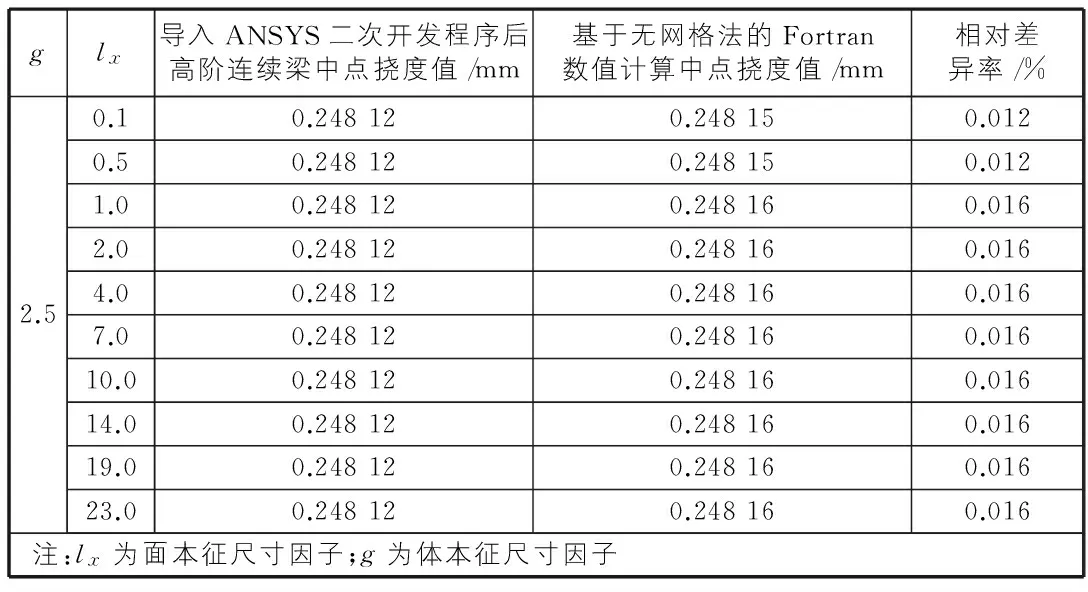
表3 尺寸因子lx變化時對高階連續梁中點撓度值

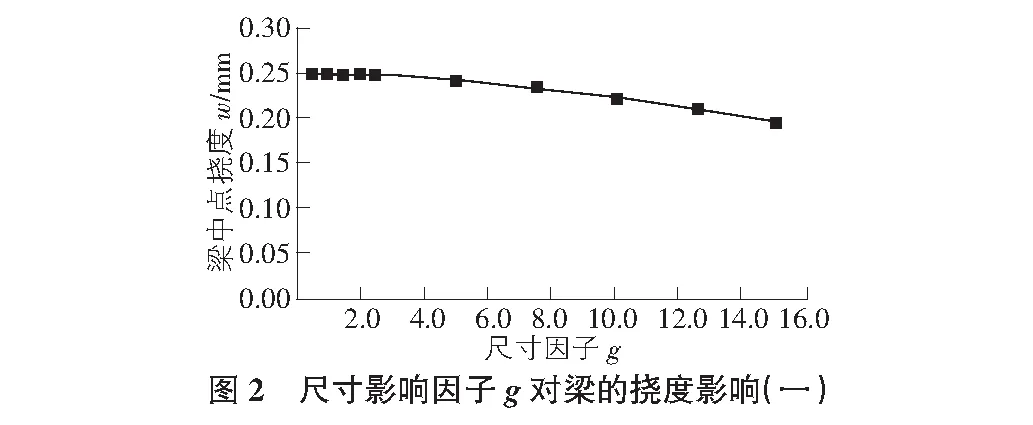
由表2,表3可知，當尺寸因子g為定值，面本征尺寸因子lx從0.1變化到23，隨著lx值的逐漸增大，對高階連續梁的撓度值影響極小；當面本征尺寸因子lx不變，g從0.5變化到15.0，對梁的撓度變化有較大影響，其影響趨勢如圖2所示。

3.2 懸臂梁的計算分析

通過導入ANSYS二次開發程序后的計算模塊分析當lx保持不變時尺寸因子g對高階連續懸臂梁的自由端撓度的影響。構建一維懸臂梁，集中力P=10 N作用在懸臂梁自由端，梁長度為5 mm，截面高度h=1 mm，厚度b=0.01 mm，橫截面面積A=h×b，彈性模量E=1.05×105MPa(面本征尺寸因子lx=2.5)，見圖3。

表4 尺寸因子g變化時對懸臂梁自由端撓度值 mm

g0.51.01.52.55.07.510.012.515.0w4.76344.75894.75194.72904.62464.46094.25064.00833.7478注:g為體本征尺寸因子;w為懸臂梁自由端撓度

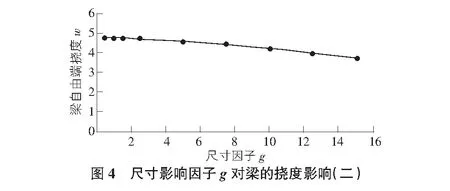
由表4數據可以看出，導入ANSYS二次開發的程序后，高階連續懸臂梁自由端撓度受到體本征尺寸因子g值的變化影響，且懸臂梁自由端撓度值變化趨勢隨g值的增大而減小(如圖4所示)。對比圖2與圖4可知梁撓度值的變化趨勢基本一致。

4 結語

基于ANSYS為用戶提供的APDL和UPFs二次開發工具，通過研究高階連續理論在有限元軟件中的應用，得出以下結論：1)利用ANSYS提供的UELMatx.F用戶子程序，將高階連續理論及尺寸因子的概念引入到ANSYS中，實現高階連續梁在有限元軟件中的應用，克服有限元軟件對高階連續結構數值模擬的局限性，并得出尺寸因子的影響趨勢。2)計算結果與基于移動最小二乘法框架的Fortran數值計算結果基本一致，通過算例驗證了該方法的合理性、可行性。3)證明該方法對移動最小二乘法在有限元軟件中應用的可行性，為高階連續理論在有限元軟件中的應用提供新思路。

[1] Xia Z C,Hutchinson J W.Crack tip fields in strain gradient plasticity[J].Journal of the Mechanics & Physics of Solids,1996,44(10):1621-1648.

[2] Fleck N A,Hutchinson J W.Strain Gradient Plasticity[J].Advances in Applied Mechanics,1997(33):295-361.

[3] Toupin R A.Elastic materials with couple-stresses[J].Archive for Rational Mechanics and Analysis,1962,11(1):385-414.

[4] 梁醒培,王 輝.應用有限元分析[M].北京：清華大學出版社,2010.

[5] Belytschko T,Krongauz Y,Organ D,et al.Meshless methods:An overview and recent developments[J].Computer Methods in Applied Mechanics & Engineering,1996,139(1-4):3-47.

[6] Belytschko T,Lu Y Y,Gu L.Element-Free Galerkin methods[J].International Journal for Numerical Methods in Engineering,1994,37(2):229-256.

[7] 李 雷,謝水生,黃國杰.應變梯度塑性理論下超薄梁彎曲中尺度效應的數值研究[J].工程力學,2006,23(3):44-48.

[8] 李 莉,陳萬吉,鄭 楠.修正偶應力理論層合薄板穩定性模型及尺度效應[J].工程力學,2013,30(5):1-7.

[9] Sun Y,Liew K M.The buckling of single-walled carbon nanotubes upon bending:The higher order gradient continuum and mesh-free method[J].Computer Methods in Applied Mechanics & Engineering,2008,197(33-40):3001-3013.

[10] Sun Y,Liew K M.Application of the higher-order Cauchy-Born rule in mesh-free continuum and multiscale simulation of carbon nanotubes[J].International Journal for Numerical Methods in Engineering,2010,75(10):1238-1258.

[11] 師 訪.ANSYS二次開發及應用實例詳解[M].北京：中國水利水電出版社,2012.

[12] 張 雄,劉 巖.無網格法(精)[M].北京：清華大學出版社,2004.