GPS/BDS組合的精密單點定位算法實現

王趁香，徐愛功，葛茂榮，祝會忠，高 猛

(1.遼寧工程技術大學 測繪與地理科學學院，遼寧 阜新 123000；2.德國GFZ地學研究中心，Potsdam A1714473，德國)

0 引言

全球衛星導航系統(global navigation satellite system，GNSS)已經在各行各業中得到了廣泛的應用，精密單點定位技術(precise point positioning，PPP)是指利用載波相位觀測值以及利用國際GNSS服務組織(International GNSS Service，IGS)提供的精密星歷和精密衛星鐘差產品，采用有效的參數估計方法和精細的誤差改正模型直接獲得載體在國際地球參考框架(international terrestrial reference frame，ITRF)下的絕對坐標的方法。文獻[1]提到全球有影響力的國家或集團紛紛構建自己的GNSS，逐漸形成多GNSS格局，美國的全球定位系統(global positioning system，GPS)經過20多年的研究和實驗，于1994-03完成了24顆衛星在軌的完整系統網絡，實現全球98 %地區的覆蓋。文獻[2]提到截至2016-06，中國自主開發的北斗衛星導航系統(BeiDou navigation satellite system，BDS)由7顆地球靜止軌道(geostationary Earth orbit，GEO)衛星、8顆傾斜地球同步軌道(inclined Earth geosynchronous satellite orbit，IGSO)衛星和7顆中高度地球軌道(medium altitude Earth orbit，MEO)衛星(其中1顆為測試衛星)組成，目前已實現了區域導航能力。文獻[3]提到隨著各國導航系統的建立，多衛星導航系統組合導航定位成為了必然趨勢，多衛星導航系統組合PPP不僅增加了可見衛星數，同時改善了衛星幾何強度，在誤差處理方面提供了更多的觀測數據，為實現PPP模糊度快速固定與高精度定位創造了條件。文獻[4-5]指出國內外許多學者對組合導航定位進行了研究，研究表明在中國區域內的GPS/BDS和GPS/GLONASS組合系統的覆蓋性能力相比于GPS、BDS和GLONASS單系統更優。然而對3系統組合精密單點定位的理論研究并不完善，此方向也成為今后GNSS多系統融合精密單點定位算法的研究趨勢。目前，精密單點定位存在著解算模型中參數較多、定位收斂時間長、定位精度相比差分定位要差等問題，如何利用多衛星導航系統組合進行精密單點定位，解決精密單點定位中存在的定位精度及收斂時間問題，提高定位的精度，縮短定位的收斂時間，成為相關研究的重點。經過各國多年的研究，PPP定位精度逐漸提高。文獻[6]提出在測碼偽距與測碼偽距觀測值間、載波相位與載波相位觀測值間分別形成雙頻消電離層組合的PPP模型，獲得了厘米級的定位精度。文獻[7]提出了非差精密單點定位方法，處理長時間靜態觀測數據的結果精度達到厘米級。

本文借鑒GPS PPP的算法與數學模型，以GPS和BDS單系統高精度導航定位的發展與應用為基礎，進行GPS/BDS組合PPP算法與定位精度方面的研究。

1 數學模型和數據處理策略

1.1 時間與空間基準的統一

BDS的時間基準采用北斗時(BDS time，BDT)。BDT的起算時刻為UTC 2006-01-01 T 00：00：00，秒長為原子時秒長，采用星期(周)和秒計數，GPS時是GPS采用的時間系統，GPS時(GPS time，GPST)的起算時刻為世界時(universal time cood，UTC)1980-01-06 T 00：00：00，在起始時刻GPST與UTC嚴格對齊，GPS時與國際原子時(international atomic time，TAI)相差19 s，通過將UTC(NTSC)與國際UTC建立聯系，BDT與UTC之間的偏差保持在100 ns以內[5]。GPST與BDT相差604 814 s，轉換關系為

GPST=BDT+604 814。

(1)

2000國家大地坐標系(China geodetic coordinate system 2000，CGCS2000)被我國BDS所采用，CGCS2000坐標系的原點定義在包括海洋和大氣在內的整個地球的質量中心，空間尺度同地心局部框架的地心坐標時(geocentric coordinate time，TCG)時間坐標一致，單位為m，定向由國際時間局(International Time Bureau，BIH)1984.0定向給定，并且其時間演變由整個地球上水平構造運動無凈旋轉條件保證[8-9]。CGCS2000坐標系是右手地固直角坐標系：原點在地球的質心；Z軸指向國際地球自轉服務組織(International Earth Rotation Service，IERS)發布的參考極方向；X軸為IERS參考子午面與通過原點且同Z軸正交的赤道面的交線；Y軸垂直于ZOX平面構成右手坐標系[10-11]。CGCS2000坐標系的參考橢球是一個旋轉橢球，其幾何中心與坐標系的原點重合，旋轉軸與坐標系的Z軸一致[12]。WGS-84坐標系(world geodetic system-1984 coordinate system，WGS-84)為GPS所采用，與CGCS2000坐標系在定義上是一致的，其中坐標原點、空間尺度、定向及其演變都是相同的，采用的參考橢球也是非常相近的[13-18]。

1.2 數學模型

GSP/BDS組合采用L1、L2頻率上的相位和偽距觀測值進行無電離層組合的觀測值來消除電離層延遲一階項的影響，基本觀測方程[14]為

(2)

式中：上標G、B代表GPS系統和BDS系統；i為頻率；Li為各載波相位觀測值；P為偽距觀測值；ρ為信號發射時刻的衛星位置到信號接收時刻接收機位置之間的幾何距離；c為真空中的光速，c=2.997 924 58×108m/s；λi為相應頻率的波長；δT為接收機鐘差；δt為衛星鐘差；T為對流層延遲誤差；Ii為Li各載波相位的電離層延遲引起的距離誤差；dmul為多路徑效應引起的誤差；dtide為海潮等的潮波引起的誤差；drel為相對論效應引起的誤差；Ni為對應頻率相位觀測值的整周模糊度；εL為載波相位的觀測噪聲以及未被模型化的各項誤差的影響；εp為偽距觀測噪聲以及未被模型化的各項誤差的影響。

1.3 數據處理策略

實驗中主要對與衛星有關的誤差(衛星鐘差、衛星天線相位中心偏差、相位纏繞等)、與接收機有關的誤差(接收機鐘差、接收機天線相位中心偏差、地球固體潮等)、與信號傳播有關的誤差(對流層延遲誤差、電離層延遲誤差、多路徑效應等)3類誤差通過模型改正以達到理想的誤差處理效果，如天線相位偏差的影響利用參數所建立的改正模型消除，對流層延遲采用Sassatamoinen+隨機游走模型減弱，電離層延遲通過雙頻消電離層組合模型消除[15-19]。實驗采用的截止高度角為7°，衛星軌道和衛星鐘差均采用國際GNSS服務組織IGS提供的采樣間隔為30 s的精密軌道和30 s的精密鐘差，靜態PPP 實驗時測站坐標當常參數估計，在動態PPP數據處理時增加測站速率約束條件，對于截止高度角、相位纏繞改正模型、固體潮汐改正模型、相對論效應改正模型與靜態PPP相同，具體的PPP數據處理策略如表1所示。

表1 PPP數據處理策略

在數據預處理過程中，本文實驗在參數估計時采用間接平差法，平差后易于求得待求量的最佳估計及精度信息，若L為觀測值，B為系數矩陣且為滿秩矩陣，d為改正數，X0為初始值，D為近似改正數，P為參數矩陣，則具體步驟如下：

(3)

式中：

令觀測值的近似值為l0，有l=L-(BX0+D)=L-l0；

(4)

(5)

利用數學上求極值的方法對V求極值，即VTPV=min，有BTPV=0；

(6)

聯立方程解得到參數的估計值

(7)

得到待估參數的值即最終的平差結果

(8)

2 實驗與結果分析

實驗采用MIZU、PBRI、SHAO、SMST、AIRA、BJFS、CHAN觀測站上多模接收機同步接收的GPS和BDS 2016-10-03—2016-10-05 3 d的觀測數據進行GPS、BDS、GPS/BDS組合3種模式下不同計算時長(2、6、12、24 h)的靜態以及動態PPP實驗。觀測站MIZU、PBRI、SHAO、SMST、AIRA、BJFS、CHAN的經度、緯度以及天線類型如表2所示。為了分析定位精度，以IGS中心發布的第1 917個星期的測站坐標作為參考值。所選測站的觀測數據采樣間隔為30 s，精密產品采用IGS提供的GPS 30 s精密星歷和30 s精密鐘差產品，使用IGS提供的ANTEX文件改正GPS衛星端和接收機端天線相位中心偏移和天線相位中心變化。

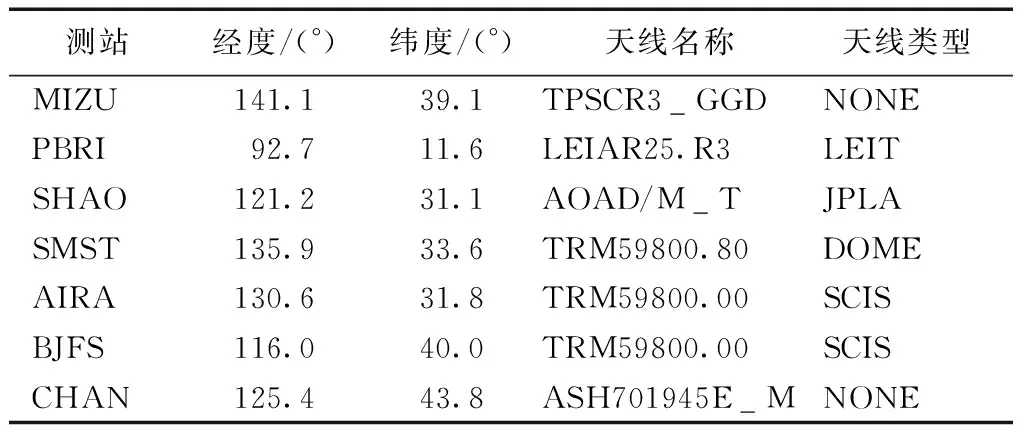
表2 測站相關信息

以MIZU為例，計算時長為2 h，3 d的觀測數據共36個觀測歷元；計算時長為6 h，3 d的觀測數據為12個觀測歷元；計算時長為12 h，3 d的觀測數據共6個歷元；計算時長為24 h，3 d的觀測數據為3個觀測歷元。以IGS中心發布的第1 917個星期的測站坐標解作為參考值，分別計算出每個歷元所獲得的測站坐標在東(E)方向、北(N)方向和天(U)方向的定位誤差。MIZU測站可見衛星數如圖1所示。BDS可見衛星數有3～8顆，GPS可見衛星數有7～12顆，GPS/BDS組合系統可見衛星數有12～20顆，可見衛星數均能滿足靜態和動態PPP實驗。MIZU測站位置精度衰減因子(position dilution of precision，PDOP)值的變化如圖2所示，GPS/BDS組合系統的PDOP值小于GPS和BDS單系統的PDOP值，說明GPS/BDS組合系統的衛星結構優于單系統的衛星結構。

2.1 靜態PPP實驗

測站MIZU GPS、BDS和GPS/BDS組合3種模式下靜態PPP實驗結果如圖3至圖6所示。

計算分析時，首先將觀測站MIZU 24 h的觀測數據分為36個觀測時段，即每個子時段2 h，3 d一共36個子時段，以IGS第1 917個星期的坐標作為參考值，分別計算出每個時段所獲得的測站坐標在E、N和U方向的定位誤差，BDS、GPS和GPS/BDS組合系統2 h的定位誤差結果如圖3所示。BDS在E和N2個方向的定位誤差一般在5 cm左右，U方向誤差在6 cm左右；GPS在E和N2個方向的定位誤差一般在3.8 cm左右，U方向誤差在5.5 cm左右；GPS/BDS組合在E和N2個方向的定位誤差一般在3 cm左右，U方向誤差在4.5 cm左右。

然后，將觀測站MIZU 24 h的觀測數據分為4個觀測時段，即每個子時段6 h，3 d一共12個子時段，以IGS第1 917個星期的坐標解作為參考值，分別計算出每個時段所獲得的測站坐標在E、N和U方向的定位誤差，BDS、GPS和GPS/BDS組合系統6 h的定位誤差結果如圖4所示。BDS在E和N2個方向的定位誤差一般在3 cm左右，U方向誤差達到3.8 cm；GPS在E和N2個方向的定位誤差一般在2 cm左右，U方向誤差在3.5 cm左右；GPS/BDS組合在E和N2個方向的定位誤差一般在1.8 cm左右，U方向誤差為2.3 cm左右。

第三，將觀測站MIZU 24 h的觀測數據分為2個觀測時段，即每個子時段12 h，3 d一共6個子時段，以IGS第1 917個星期的坐標解作為參考值，分別計算出每個時段所獲得的測站坐標在E、N和U方向的定位誤差，BDS、GPS和GPS/BDS組合系統12 h的定位誤差結果如圖5所示。BDS在E和N2個方向的定位誤差一般在2.5 cm左右，個別誤差達到3 cm，U方向誤差一般在3 cm左右；GPS在E方向的定位誤差一般在2 cm左右，N方向誤差一般在1 cm左右，U方向誤差達到3.5 cm；GPS/BDS組合在E方向的定位誤差一般在1.8 cm左右，N方向的定位誤差一般在0.8 cm左右，U方向誤差為2 cm左右。

最后，將觀測站MIZU 24 h的觀測數據為1個觀測時段，即每個子時段24 h，3 d一共3個子時段，以IGS第1 917個星期的坐標解作為參考值，分別計算出每個時段所獲得的測站坐標在E、N和U方向的定位誤差，BDS、GPS和GPS/BDS組合系統24 h的定位誤差結果如圖6所示。BDS 在E、N、U方向24 h的定位誤差一般在2 cm左右，一小部分誤差超過了2 cm；GPS 在E、N、U方向24 h的定位誤差一般在1.5 cm左右，一部分誤差超過了1.5 cm；GPS/BDS組合在E、N、U方向24 h定位誤差一般為1 cm左右，個別超過1.5 cm。

實驗所采用的7個測站數據進行靜態PPP的均方根(root mean square，RMS)值如表3所示。

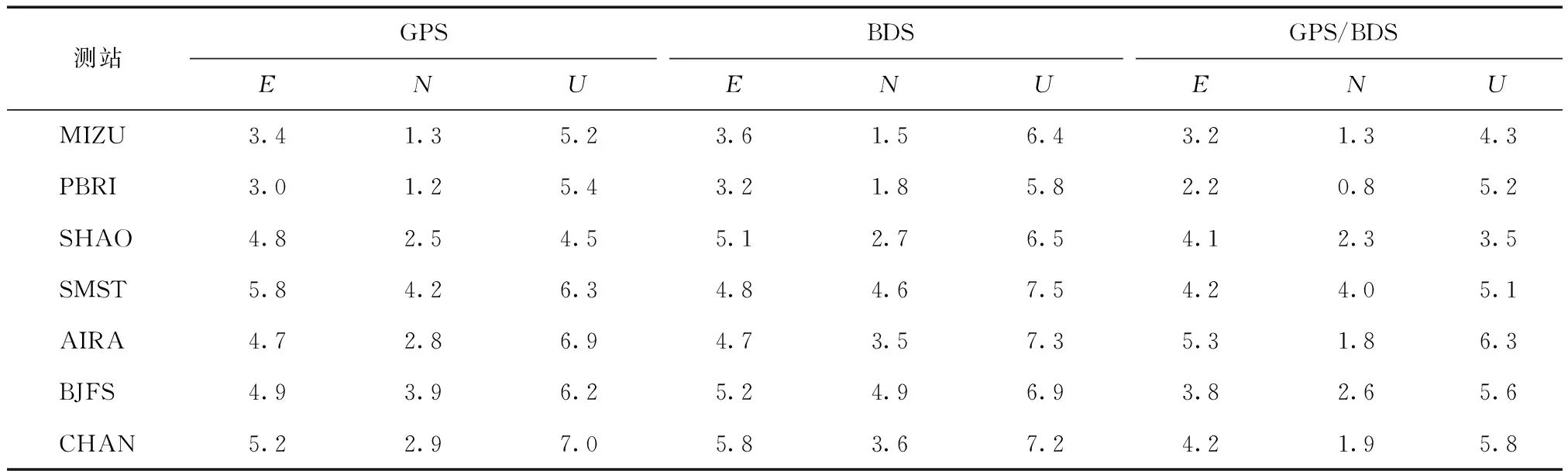
cm

2.2 動態PPP實驗

以MIZU測站靜態數據進行GPS、BDS和GPS/BDS組合3種模式下動態實驗結果如圖8至圖10所示。

首先將觀測站MIZU 24 h的觀測數據分為36個觀測時段，即每個子時段2 h，3 d一共36個子時段，以IGS第1 917個星期的坐標作為參考值，分別計算出每個時段所獲得的測站坐標在E、N和U方向的定位誤差，其結果如圖7所示。BDS 在E、N、U3個方向2 h的定位誤差一般在5.5 cm左右，一小部分誤差超過了6 cm；GPS 在E、N、U3個方向2 h的定位誤差一般在5 cm左右，一小部分誤差超過了5.5 cm；GPS/BDS組合在E、N、U3個方向2 h定位誤差一般為4.5 cm左右。

然后，將觀測站MIZU 24 h的觀測數據分為4個觀測時段，即每個子時段6 h，3 d一共12個子時段，以IGS第1 917個星期的坐標解作為參考值，分別計算出每個時段所獲得的測站坐標在E、N和U方向的定位誤差，BDS、GPS和GPS/BDS組合系統6 h的定位誤差結果如圖8所示。BDS在E和N2個方向的定位誤差一般在2.5 cm左右，個別誤差達到3 cm，U方向誤差一般在3 cm左右；GPS在E方向的定位誤差一般在2 cm左右，N方向誤差一般在1.5 cm左右，U方向誤差一般在3.5 cm左右；GPS/BDS組合在E方向的定位誤差一般在1.5 cm左右，N方向的定位誤差一般在0.5 cm左右，U方向誤差為2.3 cm左右。

第三，將觀測站MIZU 24 h的觀測數據分為2個觀測時段，即每個子時段12 h，3 d一共6個子時段，以IGS第1 917個星期的坐標解作為參考值，分別計算出每個時段所獲得的測站坐標在E、N和U方向的定位誤差，BDS、GPS和GPS/BDS組合系統12 h的定位誤差結果如圖9所示。BDS在E和N2個方向的定位誤差一般在2.5 cm左右，個別誤差達到3 cm，U方向誤差一般在3.5 cm左右；GPS在E方向的定位誤差一般在2.3 cm左右，N方向誤差一般在1 cm左右，U方向誤差一般在3.5 cm左右；GPS/BDS組合在E方向的定位誤差一般在2 cm左右，N方向的定位誤差一般在0.8 cm左右，U方向誤差為2.3 cm左右。

再者，將觀測站MIZU 24 h的觀測數據為1個觀測時段，即每個子時段24 h，3 d一共3個子時段，以IGS第1 917個星期的坐標解作為參考值，分別計算出每個時段所獲得的測站坐標在E、N和U方向的定位誤差，BDS、GPS和GPS/BDS組合系統24 h的定位誤差結果如圖10所示。BDS在E、N、U方向的定位誤差一般在2.5 cm左右，個別誤差達到3 cm；GPS 在E方向的定位誤差一般在2 cm左右，N方向誤差一般在1.5 cm左右，U方向誤差一般在3.5 cm左右；GPS/BDS組合在E方向的定位誤差一般在1.5 cm左右，N方向的定位誤差一般在0.8 cm左右，U方向誤差為2 cm左右。

實驗所采用的7個測站數據進行動態PPP的RMS值如表4所示。

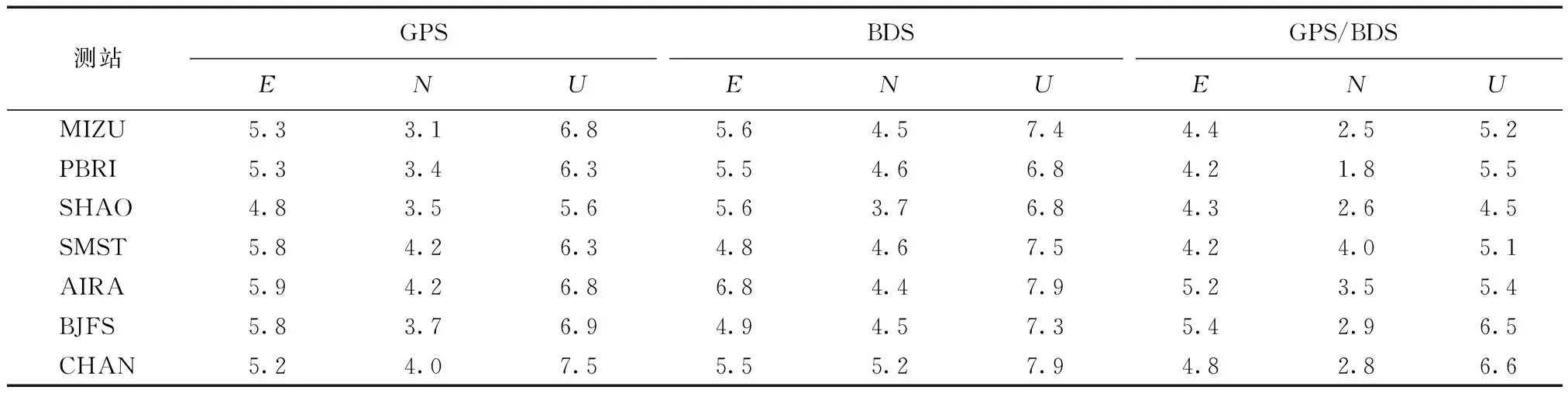
表4 7個測站動態PPP RMS值 cm

3 結束語

通過自編軟件對MIZU、PBRI、SHAO、SMST、AIRA、BJFS、CHAN 7個觀測站2016-10-03—2016-10-05 3 d的實測數據進行靜態以及動態PPP實驗，從MIZU實驗結果可以得出，GPS/BDS組合系統的靜態以及動態PPP精度明顯高于單系統定位精度。從表3和表4中統計的7個觀測站RMS值中可以看出，GPS/BDS組合系統RMS值在E、N、U方向小于單系統。同時，通過實驗可知GPS/BDS組合系統的可見衛星數多于GPS和BDS單系統的可見衛星數，由此可知，可見衛星數對不同系統的PPP精度會產生一定的影響，可見衛星數越多，定位精度相對越高。

本文采用靜態數據模擬動態解算給出的精度指標要優于用實測動態數據定位解算給出的精度指標，并且所選測站大多在赤道附近以及所采用的測站比較少，觀測時間也比較短，并且在數據處理的時候采用的高度角比較低，由此在同一時刻可以看到更多的衛星可數，這樣更有利于數據觀測；因此動態結果更好一些。武漢大學的張小紅教授早在2006年采用精密單點定位技術就獲得了幾個厘米的動態定位精度。研究多測站動態數據下精密單點定位的精度問題是下一步研究的重點。

[1] 楊元喜，李金龍，徐君毅，等.中國北斗衛星導航系統對全球PNT用戶的貢獻[J].科學通報，2011，56(21)：1734-1740.

[2] 黃令勇，呂志平，劉毅錕，等.三頻BDS電離層延遲改正分析[J].測繪科學，2015，40(3)：12-15.

[3] 徐杰，孟黎，仁超，等.對流層延遲改正中投影函數的研究[J].大地測量與地球動力學，2008，28(5)：120-124.

[4] 金 彪.GPS/GLONASS /COMPASS 組合定向算法研究及程序實現[D].武漢：武漢大學，2012.

[5] 李建文.GPS/GLONASS 組合精密單點定位理論與方法[D].徐州：中國礦業大學，2008.

[6] 涂銳，黃觀文，凌晴.GPS單頻精密單點定位的研究實現[J].測繪科學，2011，36(3)：68-72.

[7] 姜衛平，李昭，邱蕾.一種最新的經驗投影函數GMF分析[J].大地測量與地球動力學，2009，29(5)：85-89.

[8] 李征航，張小紅.衛星導航定位新技術及高精度數據處理方法[M].武漢：武漢大學出版社，2009：23-24.

[9] 徐宗秋，徐愛功，高揚，等.對流層延遲參數與坐標參數的相關性研究[J].測繪通報，2013(1)：25-28.

[10] 劉旭春，易武，張正祿，等.高精度GPS系統硬件延遲解算方法研究[J].宇航學報，2007，28(2)：310-314.

[11] 涂銳，黃觀文，凌晴.GPS單頻精密單點定位的研究實現[J].測繪科學，2011，36(3)：68-72.

[12] 吳波，吳瑞琰，黨亞民，等.利用BDS/Galileo廣播星歷的位置及速度計算[J].導航定位學報，2016，4(3)：51-54.

[13] 張小紅，郭斐，李星星，等.GPS/GLONASS組合精密單點定位研究[J].武漢大學學報(信息科學版)，2010，35(1)：9-12.

[14] 臧楠.BDS/GNSS精密單點定位算法研究[D].西安：長安大學，2015.

[15] GRIFFITHS J，RAY J R.On the precision and accuracy of IGS orbits[J].Journal of Geodesy，2009，83(4)：277-287.

[16] ZHAO Q.Initial results of precise orbit and clock determina-tion for COMPASS navigation satellite system[J].Journal of Geodesy，2013，26(1)：1-12.

[17] XU A，XU Z，GE M R，et al.Estimating zenith tropospheric delays from BeiDou navigation satellite system observations[J].Sensors，2013，13(4)：4514-4526.

[18] LI X X，GE M R，ZHANG H P，et al.A method for improving uncalibrated phase delay estimation and ambiguity-fixingin real-time precise point positiong[J].Journal of Geodesy，2013，87(5)：405-416.

[19] XU Z，XU A，XU，X.Research on the correlation of troposphere delay parameters in GPS[J].Advances in Information Sciences and Service Sciences，2012，4(22)：336-343.