問題引導下的嘗試策略在教學中的應用
——以“勻變速直線運動的速度與位移的關系”為例
潘華君 姜 勝 顧愛芬
(江蘇省宜興第一中學,江蘇 宜興 214200)
1 嘗試教學簡介
嘗試教學是一種教學理念,一種教學方式,更是一種教學精神,[1]其實質,就是讓學生在一定的問題情景中主動嘗試,通過對“預設問題”的不斷“試錯”從而生成新問題,在生本、生生、師生的多向交流中獲得成功.江蘇省常州市教育科學研究院院長邱學華先生設計的基本模式有7個環節:準備練習—出示嘗試題—自學課本—嘗試練習—學生討論—教師講解—第二次嘗試練習.[1]在此基礎上,亦有人提出了多種模式.但無論何種模式,其核心是讓學生自己閱讀和思考.[2]另一方面,蘇聯教學論專家馬赫穆托夫等人創立的“問題教學理論”認為:人們在認識活動中,當遇到現有條件或已有的經驗尚無法解決的實際問題時,就會產生一種懷疑、探索的心理狀態,從而激活主體思維,試圖去找出解決問題的辦法.[3]基于此,結合兩者優點的問題引導下的嘗試教學法,以問題引導為教師“導”的方式,以嘗試為學生“學”的具體操作方式,讓學生在實踐中獲取知識,在體驗中感知成功的樂趣,從而培養學生敢于探究、勇于實踐的科學素養.下文就以“勻變速直線運動的速度與位移的關系”新課教學為例,做一次教學嘗試.
2 問題引導下的嘗試教學法的實踐應用
2.1 嘗試感知兩物理量間的定性關系
師:播放交警在車禍現場測量的圖片.交警從剎車痕跡的長短可以判斷當時車速的大小: ① 假如我們把汽車剎車的過程看成是一個勻減速運動的過程,此處的剎車痕跡代表了哪一個物理量? ② 從物理學的角度看,這種判斷的依據是什么?
生:此處痕跡表示剎車過程中汽車的位移;在加速度一定的前提下,初速度越大,剎車時間越長,位移也就越大.
師:通過上述實例的分析,我們明確了勻變速直線運動中的速度與位移的定性關系,那么這兩者間的定量關系是怎樣的呢?這就是本節的主題.
設計理由:本節課,以一張“交警在車禍現場處理”的圖片引入,其目的有: ① 相較于人教版以“子彈從槍筒里射出”為例,本節課的引入更接近學生的生活,更能在新課的開始吸引學生的眼球,把學生的注意力和思緒拉回課堂; ② 以圖片入手,可以培養學生的觀察能力以及構建理想運動模型的能力; ③ 以客觀的現實,引發學生的對行車安全的思考,將“安全行車、尊重生命”蘊含于本節課中; ④ 通過師生的問答方式,在學生感知定性關系后,拋出新問題——尋找定性關系.
2.2 嘗試尋找兩物理量的定量關系
師:若汽車在做勻加速直線運動,初速度為5 m/s,加速度大小為1 m/s2,則當位移為100 m時,末速度多大?(只要求學生畫出運動示意圖、思考解決的方法,不需要具體的解答.)
生A:先通過位移與時間的關系式求出運動時間t,然后將t代入速度與時間的關系式求出末速度.
師:A同學的思路完全正確.在他的方法中,為了求出末速度,先求了一個運動的時間,即運動時間t僅是起到一個橋梁的作用,聯系著“速度與時間的關系式”和“位移與時間的關系式”,這樣的方法正確但略顯復雜.我們能不能找一個更簡單的處理方法,即能不能直接找出一個速度與位移的關系式?如何找這個公式?
生B:只要把t消掉就可以直接推導出速度與位移的關系式.
師:好,我們就按照B同學的方法,請同學自行推導勻變速直線運動的速度與位移的關系式,并于同桌相互交流.(學生自行推導,教師在教室里巡查,注意收集學生的典型錯誤;待學生推導好后,投影學生的作答)
設計理由: ① 通過一道例題的設計,教師通過恰當的引導,讓學生意思到用已有的知識求解時較為復雜,從引導學生思考“時間t的作用”和“有沒有更簡單的處理方法”,從而尋找到“消元”的方法,為得出定量關系式打下基礎.② 與人教版本節教材上例1的一個區別是,在設計本題時賦予其一個初速度.這是因為,基于以往的教學經驗,若設計一個初速度為0的勻加速運動,部分學生在自行推導公式時,往往就會直接推導初速度為0條件下的速度與位移的關系式.為了避免以上情況,同時使推導式更具有一般性,特作以上修改.③ 從一線教學現場觀察發現,學生的數學運算能力比較弱,本嘗試題的設計目的就在于給予學生思考、分析、運算的時間,讓學生的思維在“慢教學”的過程中逐漸向深處延伸.④ 在學生的求解中,還有少部分學生會先從位移公式入手,利用求根公式求出時間的表達式再代入速度公式,這個求解方式既復雜又難以得到最終需要的表達式,教學中建議要適當引導.
2.3 嘗試應用,加深理解
師:同學們通過消元法推導出了勻變速直線運動速度與位移的關系式:2ax=vt2-v02.結合上節課所學的位移與時間的關系式以及做過的習題,請你思考一下,在哪些情景中,利用速度與位移的關系式求解更簡潔?
生:這個表達式涉及的物理量有加速度、位移、初末速度,不涉及時間,因此,該表達式主要用于題目中不涉及時間的問題.
師:是的,這個表達式提出的目的就是在于解決不涉及時間或者是時間難以測量的問題.例如,這節課開頭所展示的“車禍現場”的圖片,車禍發生于“過去時空”且時間短,交警在處理時無法測量時間,此時只能測量位移、估測剎車時的加速度,從而判斷剎車前的速度.這也就是該表達式的物理意義所在.
師:請同學們依據前面的分析,選擇合適的公式,解決下面這個問題“某汽車在做直線運動,初速度為108 km/h,剎車時的加速度大小為5 m/s2,一段時間后速度減為36 km/h,求汽車在該過程中的位移”.(學生獨立作答)
師:(出示教師事先準備好的一份典型的錯誤解答,如沒有統一單位的、沒有規定正方向的、加速度沒有代入負值的等,進行投影展示)屏幕上展示的是一位同學的解答過程,對比一下你的解答,請同學們來“找茬”?
生C: 我發現它有兩個錯誤: ① 它在進行數值運算時需要統一單位; ② 剎車過程中,汽車在做勻減速運動,加速度應代入負值.
生D:還有一個錯誤,沒有規定正方向.只有規定了正方向,用正負表示矢量的方向才有意義.
師:兩位同學思考得很深入.結合兩位同學的分析,再看這個表達式2ax=vt2-v02,式中4個量均是矢量,在直線運動問題中,可規定正方向,利用正負表示各個矢量的方向,如以初速度方向為正:加速和減速時,a分別應代入什么值?末速度為正值或負值時,有何意義?位移為正值或負值時,有何意義?
學生齊聲回答:加速時a與初速度方向相同,代入正值,減速時a與初速度方向相反,應代入負值;末速度為正值,表示與規定正方向同向,末速度為負值時,表示與規定正方向反向;位移為正值,表示末位置在初位置的正方向前,位移為負值時,末位置在初位置的負方向上.
設計理由: ① 本章教學的一個難點就是公式較多,學生難以快速、正確的選擇,通過對兩個位移公式的比較,讓學生感知“速度與位移關系式”適用的情景,幫助學生逐漸學會選擇的依據; ② 運動學問題處理的一個重點就是矢量的處理,在上述設計中,沒有直接討論矢量符號的問題,而是通過一個“減速問題”,讓學生“試錯”,在嘗試中發現問題,在嘗試中掌握處理的方法; ③ 此處以預測的典型錯誤解法讓學生“找茬”而不投影學生的錯誤解答,其目的在于保護學生的積極性,防止出現被投影作業的學生出現難堪等不良情緒.
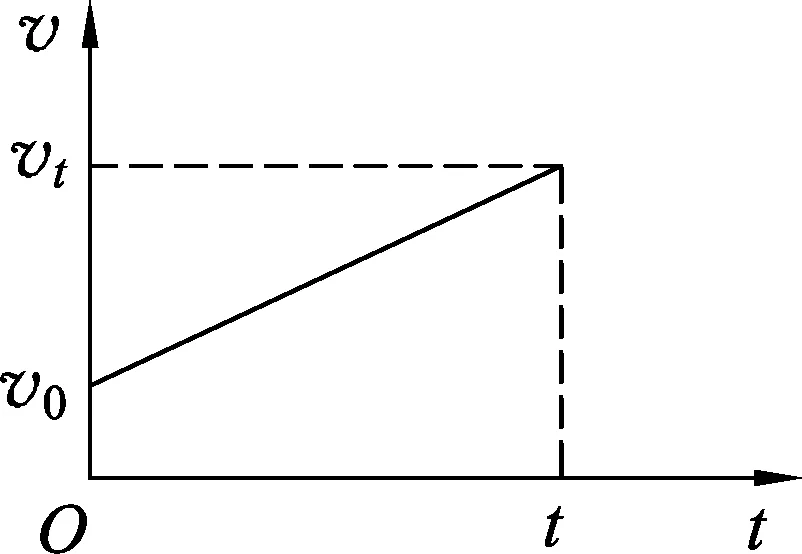
圖1 v-t圖
2.4 嘗試尋找勻變速直線運動的時空特征
師:物理量間的關系可以通過公式來表達,也可以通過圖像來描述,且圖像更具有直觀性.例如,圖1描述的是某一物體在做勻加速直線運動時的v-t圖,請你利用圖上相關數據求出t時間內的位移和加速度?
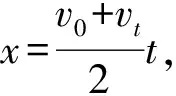
師:利用這兩個關系式,能不能推導出速度與位移的關系式?
生:利用消元法,消去t即可,如
師:對比兩種推導方法,顯然第二種方法更簡潔.以勻加速直線運動為例,從v-t圖可知,速度隨時間的變化關系是什么?
生:速度隨時間均勻增加.
師:如果以縱軸表示速度,橫軸表示位移,v-x圖線還是一條直線,即還符合y=kx+b的形式嗎?如果不是,如何修改坐標,才能得到直線?
生:不是直線圖像了,只有把縱軸修改為v2才會是直線關系.
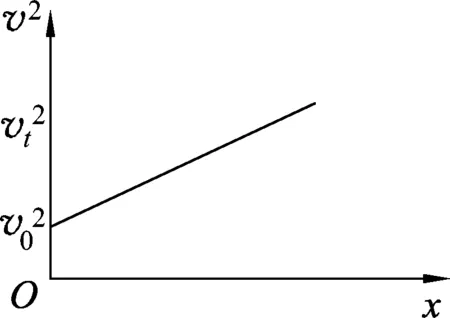
圖2 v2-x圖
師:從圖1和圖2可知:從時間角度而言,勻變速直線運動的速度隨時間均勻變化,即等時間有相等的速度改變量;從空間角度而言,勻變速直線運動的速度的平方隨位移均勻變化,即等位移有相等的v2改變量.[4]這就是勻變速直線運動的時空特征.當然后者相比前者,在描述上略顯復雜.通常情況下,我們一般研究的是速度與時間的關系.
設計理由: ① 在上述設計中,速度時間圖有兩重作用,一是利用速度時間圖推導位移公式,讓學生感知這一最簡潔的推導方法,開拓學生的思維;二是從時間維度分析勻變速直線運動的特征.② 速度位移圖的提出,既是與教材中第6節“伽利略對直線運動的研究”相呼應,也是從空間維度分析勻變速直線運動的特征.③ 兩張圖像相互結合,強化了學生對該類運動特征的認識.④ 通過速度位移圖的分析,引導學生學會“化曲為直”的數據處理方法.
3 教學反思
以上,是在高一新授課中采用的問題引導下的嘗試教學.從內容看,通過多個嘗試問題的設置,既凸顯了本章教材的兩個重要的思想方法,即矢量處理方法和圖像方法,突出了教學的重點,也滲透了安全教育,將教學升格為教育;從操作方式看,它以問題為中心,由預設問題到生成問題,問問相連,步步深入,每一個問題都使學生的思維產生一次飛躍;從教學的實踐看,學生課堂的真實參與度高,思維容量較大,有效地提升了學生的分析問題能力和培養了他們敢于實踐的科學精神;從課后的檢測反饋情況看,學生習得情況良好,有較好的獲得感.基于此,這是一次有效的教學嘗試.

