一種實時在線診斷旋轉機械振動故障的方法

范佳卿， 肖伯樂， 高 升， 張 強

(上海發電設備成套設計研究院，上海 200240)

風機和水泵等旋轉機械廣泛應用于石油、化工、電力和冶金等行業，其設備安全運行對國民經濟的發展有著重要的意義.旋轉機械長期運行后，由于磨損、變形、松動和材料疲勞等原因，發生振動故障的概率大大增加，嚴重時造成巨大經濟損失[1-2].對旋轉機械設備進行狀態監測和故障診斷，可有效降低設備的運行維護成本，保證其安全穩定運行[3-4].因此，旋轉機械振動故障的監測和診斷研究一直是多年來的研究熱點，并且已經出現不少具有實用價值的研究成果.目前，在振動信號的監測上已有較成熟的方法和技術，在故障的診斷上常用的頻域分析由于計算量大不易完成實時計算和在線分析[5].

筆者針對旋轉機械裝置不同振動故障，實時測量其特征值，計算得出旋轉機械裝置各種振動故障工況的時域相關特征參數，完成了不同振動故障下特征值的敏感性分析，并建立了故障診斷模型.通過試驗臺對該模型進行了驗證，形成一種智能在線遠程的旋轉機械振動故障診斷方法.

1 特征值計算方法

1.1 特征值選取

振動特征值有加速度高頻峰值、高頻峰值因子、高頻Vdi3832參考值、加速度峰值、峰值因子、偏斜度、峭度、Vdi3832參考值、加速度高頻有效值、加速度有效值、速度有效值、振動烈度、加速度包絡有效值、速度包絡有效值、速度包絡噪聲值、加速度包絡噪聲值、加速度噪聲值和速度噪聲值等.根據國際國內振動標準及相關行業標準，筆者選取了其中12個振動特征值進行研究，根據定義分為有效值、峰值、峰值因子、峭度和偏斜度5類.

1.2 特征值分類

1.2.1 有效值

(1)振動烈度.

振動烈度(ISO10816)是10～1 000 Hz頻率段上原始信號的振動速度值，通常適用于檢測不平衡、不對中、碰磨、早期軸承故障、潤滑油失效和耦合故障等問題.國際和國內許多振動標準都采用振動烈度作為評估旋轉機械設備健康狀態的判斷參數[6].

為了獲取足夠的靈敏度，測量振動烈度時探頭需盡量安裝在軸承座軸向和徑向位置，如圖1和圖2所示.

圖1 水平放置旋轉機械測量點

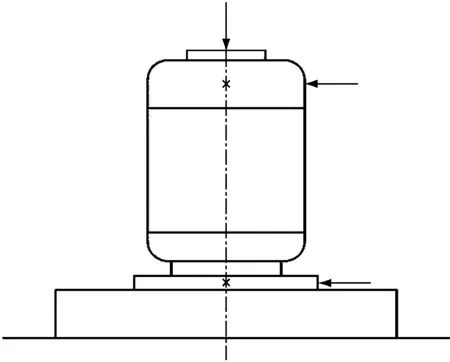
圖2 豎直放置旋轉機械測量點

根據旋轉機械底座和機械類型，振動烈度有4種不同的閾值劃分方式，如圖3所示.

(2)加速度有效值.

加速度有效值(RmsAccRaw)由加速度傳感器采集振動的原始信號得到，適用于檢測不平衡、不對中、碰磨、早期軸承故障、軸承損壞初期和潤滑油失效等問題.

(3)速度有效值.

速度有效值(RmsVelRaw)由振動加速度的原始信號得到[7]，選取T時間段，可以得到該時間段內的速度有效值大小：

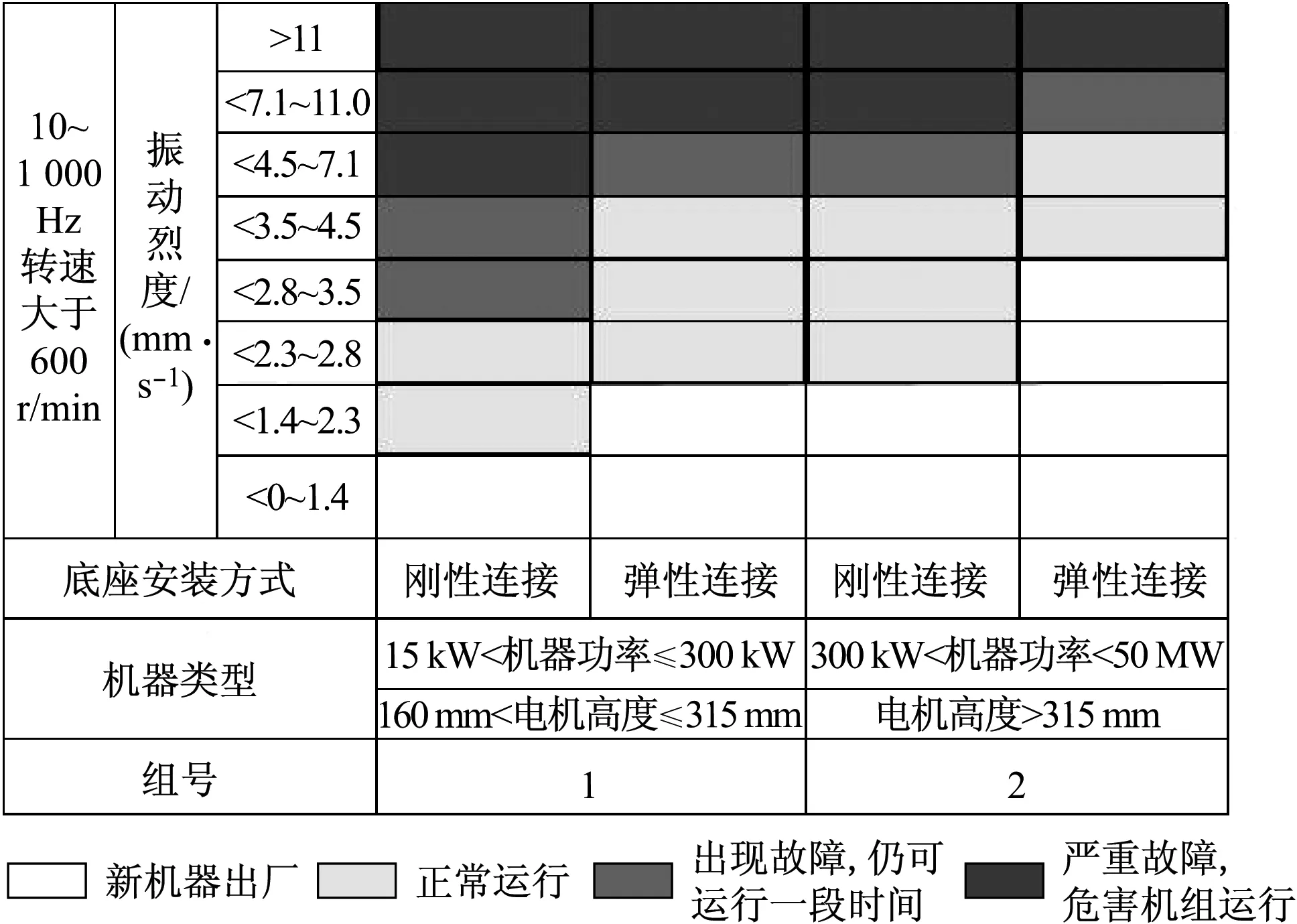
圖3 振動烈度評估表

(1)

式中：V(t)為由振動加速度原始信號積分得到的速度信號，mm/s.

速度有效值適用于檢測不平衡、不對中、碰磨、早期軸承故障、軸承損壞初期和潤滑油失效等問題.

(4)加速度高頻有效值.

加速度高頻有效值(RmsHighFrequency)由振動加速度輸入信號的高通濾波得到，適用于檢測碰磨、早期軸承故障、軸承損壞初期和潤滑油失效等問題.

(5)加速度包絡有效值.

加速度包絡有效值(RmsAccEnvelope)由振動加速度的包絡信號得到，是由SKF公司針對滾動軸承的診斷而開發的技術，能夠從早期就清晰反映滾動軸承故障的程度和原因.

(6)速度包絡有效值.

速度包絡有效值(RmsVelEnvelope)由振動加速度的包絡信號得到，適用于檢測碰磨、軸承損壞初期和潤滑油失效等問題.

1.2.2 峰值

旋轉機械振動信號的峰值是指來自環境噪聲影響的總和最大值.

(1)加速度高頻峰值.

加速度高頻峰值(PeakHighFrequency)由振動加速度輸入信號的高通濾波得到，適用于檢測碰磨、早期軸承故障、軸承損壞初期和潤滑油失效等問題.

(2)加速度峰值.

加速度峰值(PeakRaw)由振動加速度的原始信號得到，適用于檢測不平衡、不對中、碰磨、早期軸承故障、軸承損壞初期和潤滑油失效等問題.

1.2.3 峰值因子

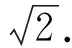
(1)高頻峰值因子.

高頻峰值因子(CrestFactorHighFrequency)由振動加速度輸入信號的高通濾波得到：

(2)

高頻峰值因子適用于檢測碰磨、早期軸承故障、軸承損壞初期和潤滑油失效等問題.

(2)峰值因子.

峰值因子(CrestFactorRaw)由振動加速度的原始信號得到：

(3)

峰值因子適用于檢測不平衡、不對中、碰磨、早期軸承故障、軸承損壞初期和潤滑油失效等問題.

1.2.4 峭度

峭度(KurtosisRaw)能有效評估在信號過程中出現峰值的次數，相當于一個加權的“峰值因子”.由于峭度對沖擊信號特別敏感，所以適用于診斷軸承早期故障，同時也適用于檢測不平衡、不對中、碰磨、軸承損壞初期和潤滑油失效等問題.

1.2.5 偏斜度

偏斜度(SkewnessRaw)能夠評估信號的不對稱程度，其值越低，正態分布越均勻，適用于檢測不平衡、不對中、碰磨和早期軸承故障等問題.

2 特征值敏感性分析和故障診斷模型

2.1 特征值敏感性分析

2.1.1 正常運行

為確定特征值在旋轉機械裝置正常運行情況下的基準值，需得到旋轉機械裝置正常運行時的特征值數據.為了與現場某風機的轉速匹配，便于后續自診斷功能的進一步開發，設置旋轉機械裝置轉速為1 492 r/min，單組記錄時間為60 s，共記錄10組，傳感器安裝在好的軸承的X、Y、Z處，即軸承徑向水平處、徑向豎直處和軸向處，剔除離群點后，記錄正常運行時的特征值參數.表1給出了Y處正常運行時的特征值.由表1可知，旋轉機械裝置中好的軸承Y處的振動烈度在符合的范圍內.

表1 正常運行時的特征值

2.1.2 不平衡故障

不平衡故障是由于轉子部件質量偏心或轉子部件損壞造成的.通過在風扇葉片上安裝磁性配重塊來模擬旋轉機械裝置發生機械不平衡故障的情況，如圖4所示.

圖4 添加配重塊模擬不平衡故障示意圖

設置旋轉機械裝置轉速為1 492 r/min，單組記錄時間為60 s，共記錄10組，可得到Y處不平衡故障時的特征值(見表2).

由表2可知，從正常運行到不平衡故障情況下，振動烈度的變化比較明顯，正常運行時其值在[0.6，0.8]mm/s內；不平衡故障時其值在[6，8]mm/s內，出現了2個較明顯的離群點，可能的原因是采集了從靜態到不平衡狀態以及從不平衡狀態回歸靜態發生改變的瞬態值；振動烈度在2種情況下的方差都較小，說明振動烈度比較穩定，離散程度小，同時在不平衡狀態下的曲線更加平滑，此時決定振動烈度的主要因素就是不平衡故障引起的離心力作用，噪聲的干擾更加細微，符合實際情況.加速度高頻有效值在正常運行和不平衡故障情況下的變化不明顯，正常運行時其值在[100，250]mm/s2內，不平衡故障時其值在[150，275]mm/s2內，方差較大，數據比較離散，不平衡故障與正常運行情況下有許多重疊的區域，說明這個變量對不平衡故障的敏感性較低.速度有效值在正常運行和不平衡故障情況下的變化明顯，正常運行時其值在[0.6，0.8]mm/s內，不平衡故障時其值在[6，8]mm/s內，方差較小，數據比較集中，不平衡故障情況下出現了一個離群點.速度包絡有效值在正常運行和不平衡故障情況下的變化不明顯，正常運行時其值在[1，5]mm/s內，不平衡故障時其值在[2.5，7]mm/s內，方差較小，數據比較集中，但是2種情況下速度包絡有效值出現了大量重合，對不平衡故障的敏感性較低.加速度峰值在正常運行和不平衡故障情況下的變化明顯，正常運行時其值在[250，800]mm/s2內，不平衡故障時其值在[600，1 200]mm/s2內，方差較大，數據比較離散，波動比較劇烈.加速度高頻峰值在正常運行和不平衡故障情況下的變化不明顯，正常運行時其值在[500，1 200]mm/s2內，不平衡故障時其值在[800，1 400]mm/s2內，方差較大，數據比較離散，波動比較劇烈，不平衡故障和正常運行情況下有許多重疊的區域，說明這個變量對于不平衡故障的敏感性較低.

表2 不平衡故障時的特征值

由表2還可知，峰值因子在正常運行和不平衡故障情況下的變化不明顯，正常運行時其值在[3.5，5.5]內，不平衡故障時其值在[3.2，5.5]內，2種情況下基本沒有變化，對不平衡故障的敏感性較低.高頻峰值因子在正常運行和不平衡故障情況下的變化明顯，正常運行時其值在[3.5，6.5]內，不平衡故障時其值在[4，7]內，2種情況下基本沒有變化，對不平衡故障的敏感性較低.峭度在正常運行和不平衡故障情況下的變化不明顯，正常運行時其值在[0，0.5]內，不平衡故障時其值在[-0.5，0.5]內，出現了大量重合的區域，對不平衡故障的敏感性低.偏斜度在正常運行和不平衡故障情況下的變化明顯，正常運行時其值在[-0.1，0.1]內，不平衡故障時其值在[0.05，0.35]內.加速度有效值在正常運行和不平衡故障情況下的變化明顯，正常運行時其值在[55，170]mm/s2內，不平衡故障時其值在[180，220]mm/s2內.加速度包絡有效值在正常運行和不平衡故障情況下的變化不明顯，正常運行時其值在[45，140]mm/s2內，不平衡故障時其值在[85，160]mm/s2內.

2.1.3 軸承故障

滾動軸承是機器中最精密的部件,其公差是其余部件的十分之一.由于各種原因，只有10%～20%的軸承能達到其設計壽命.

設置旋轉機械裝置轉速為1 492 r/min，單組記錄時間為60 s，共記錄10組，傳感器安裝在故障軸側.軸承故障如圖5所示.軸承故障時的特征值如表3所示.

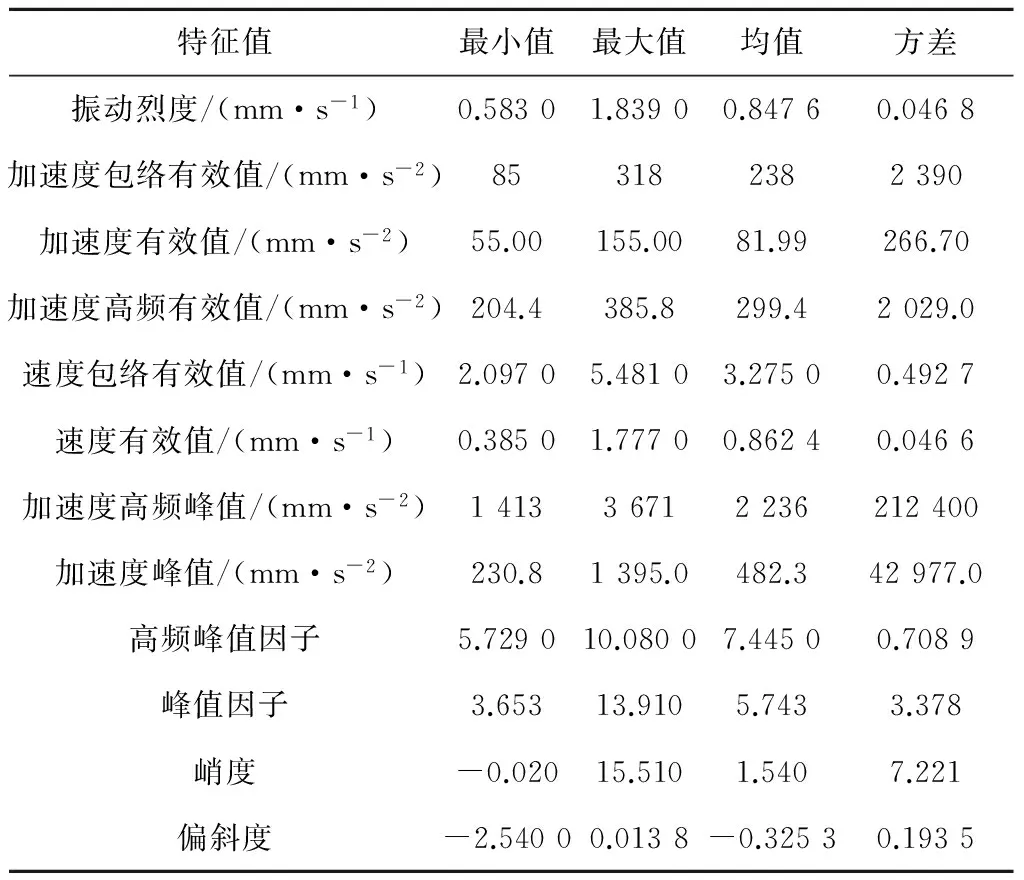
圖5 軸承故障示意圖

由表3可知，從正常運行到軸承故障情況下，振動烈度的變化并不明顯，正常運行時其值在[0.6，0.8]mm/s內，軸承故障時其值大部分在[0.6，1]mm/s內，少部分在[1.4，1.6]mm/s內，從時域幅值圖來看，軸承故障時振動烈度的波動更加厲害.加速度高頻有效值在正常運行和軸承故障情況下的變化比較明顯，正常運行時其值在[100，250]mm/s2內，軸承故障時其值在[200，380]mm/s2內.速度有效值在正常運行和軸承故障情況下的變化明顯，正常運行時其值在[0.6，0.8]mm/s內，軸承故障時其值大部分在[0.6，1]mm/s內，少部分在[1.2，1.6]mm/s內，從時域幅值圖來看，軸承故障時速度有效值的波動更加厲害.速度包絡有效值在正常運行和軸承故障情況下的變化不明顯，正常運行時其值在[1，5]mm/s內，軸承故障時其值在[2，5]mm/s內，方差較小，數據比較集中，但是2種情況下速度包絡有效值有大量重合，對軸承故障的敏感性較低.加速度峰值在正常運行和軸承故障情況下的變化不明顯，其值均在[250，800]mm/s2內，軸承故障和正常運行情況下有許多重疊的區域，說明這個變量對于軸承故障的敏感性較低.加速度高頻峰值在正常運行和軸承故障情況下的變化比較明顯，正常運行時其值在[500，1 200]mm/s2內，軸承故障時其值在[1 500，3 000]mm/s2內，方差較大，數據比較離散，波動比較劇烈.

由表3還可知，峰值因子在正常運行和軸承故障情況下的變化明顯，正常運行時其值在[3.5，5.5]內，軸承故障時其值大部分在[4，6]內，少部分在[7，10]內，雖然軸承故障和正常運行情況下的峰值因子值域區間大量重合，但是在軸承故障情況下峰值因子波動更加劇烈，最大值也比正常運行情況下大很多，能夠明顯進行區分.高頻峰值因子在正常運行和軸承故障情況下的變化明顯，正常運行時其值在[4，6]內，軸承故障時其值在[6，10]內.峭度在正常運行和軸承故障情況下的變化比較明顯，正常運行時其值在[0，0.5]內，軸承故障時其值大部分在[0，2]內，少部分在[6，12]內，峭度的絕對值變大，說明軸承故障比較嚴重.偏斜度在正常運行和軸承故障情況下的變化明顯，正常運行時其值在[-0.1，0.1]內，軸承故障時其值在[-0.5，0]內.加速度有效值在正常運行和軸承故障情況下的變化不明顯，正常運行時其值在[55，170]mm/s2內，軸承故障時其值在[60，120]mm/s2內.加速度包絡有效值在正常運行和軸承故障情況下的變化明顯，正常運行時其值在[45，140]mm/s2內，軸承故障時其值在[150，300]mm/s2內.

2.1.4 不對中故障

不對中故障包括軸系不對中和軸承不對中2種情況，本文的不對中故障屬于軸系不對中中的角度不對中.由于不對中試驗對聯軸器的角度以及內部彈簧的松緊度影響很大，對整體試驗造成的破壞太大，此處只記錄了一組數據便于觀察.通過按壓聯軸器來模擬旋轉機械裝置的不對中情況，如圖6所示.

圖6 不對中故障示意圖

設置旋轉機械裝置轉速為1 492 r/min，記錄時間為60 s，在旋轉機械裝置正常運行過程中通過按壓使聯軸器發生角度不對中故障，得到不對中故障時的特征值，如表4所示.

綜合特征值的閾值區間，可得到不平衡故障、軸承故障及不對中故障時特征值的敏感等級表，如表5所示，其中A代表對該故障非常敏感，B代表對該故障敏感，C代表對該故障敏感度一般，D代表對該故障不敏感.

表4 不對中故障時的特征值

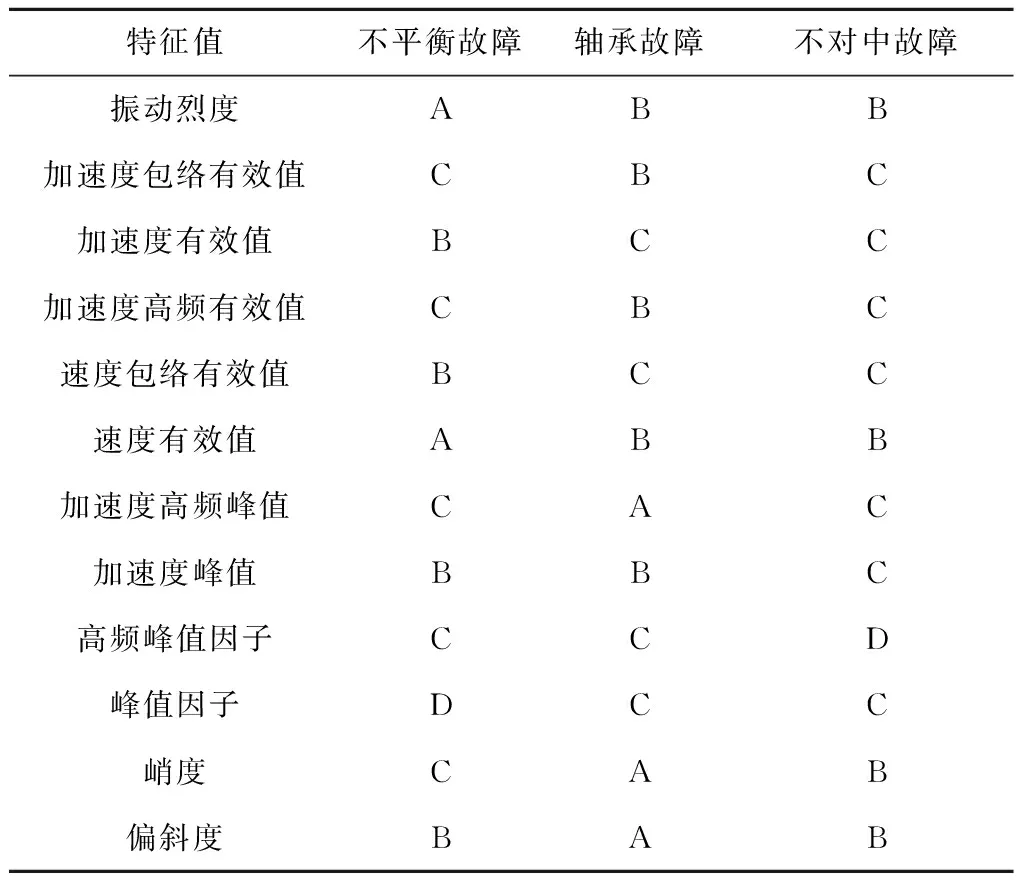
表5 特征值敏感等級表

2.2 故障診斷模型建立

設敏感等級A的特征值具有Xi的權重，敏感等級B的特征值具有Yi的權重，敏感等級C的特征值具有Zi的權重，敏感等級D的特征值具有0的權重.則總的權重Miall可表示為

Miall=MiA×Xi+MiB×Yi+MiC×Zi

(4)

式中：i=1,2,3；Miall為不平衡故障、軸承故障和不對中故障對應的總權重；MiA為敏感等級表中不平衡故障、軸承故障和不對中故障中敏感等級A的特征值個數；MiB為不平衡故障、軸承故障和不對中故障中敏感等級B的特征值個數；MiC為不平衡故障、軸承故障和不對中故障中敏感等級C的特征值個數.

當前時刻權重為Minow可表示為

Minow=MiAn×Xi+MiBn×Yi+MiCn×Zi

(5)

式中：MiAn為當前時刻不平衡故障敏感等級A的特征值個數(當且僅當特征值數值在該特征值上下閾值區間內計數)，依次類推.

當前時刻權重與總權重的比值可表示為

(6)

可知0<ηi≤1，當ηi≥0.95時，可認為發生了該類型的故障.

3 故障診斷模型應用

3.1 不平衡故障診斷

設置旋轉機械裝置轉速為1 492 r/min，在風扇葉片上安裝磁性配重塊，傳感器安裝在好的軸承X、Y、Z處，開始驗證故障診斷模型，試驗次數設置為10.結果表明，故障診斷模型進行了不平衡故障的判斷，此時ηi=100%.

3.2 軸承故障診斷

設置旋轉機械裝置轉速為1 492 r/min，傳感器安裝在故障軸承的X、Y、Z處，開始驗證故障診斷模型，試驗次數設置為10.結果表明，故障診斷模型進行了軸承故障的判斷，此時ηi=100%.

3.3 不對中故障診斷

設置旋轉機械裝置轉速為1 492 r/min，按壓聯軸器，傳感器安裝在好的軸承X、Y、Z處，開始驗證故障診斷模型，試驗次數設置為10.結果表明，故障診斷模型進行了不對中故障的判斷，此時ηi=100%.

4 結 論

(1)在12個特征值中，振動烈度、加速度有效值、速度有效值、速度包絡有效值、加速度峰值和偏斜度對不平衡故障敏感；振動烈度、加速度包絡有效值、加速度高頻有效值、速度有效值、加速度高頻峰值、加速度峰值、峭度和偏斜度對軸承故障敏感；振動烈度、速度有效值、峭度和偏斜度對不對中故障敏感.

(2)所建立的旋轉機械振動故障實時在線診斷方法，對風機和水泵等旋轉機械的現場實時監測和振動智能遠程診斷具有一定的工程應用價值.在工程應用中，由于不同旋轉機械的結構、傳動方式和環境因素等不盡相同，還需要不斷擴充振動特征值數據庫，對故障診斷模型的精度和適應度等進行更深入的研究.

[1] 張文秀, 武新芳. 風電機組狀態監測與故障診斷相關技術研究[J].電機與控制應用, 2014, 41(2): 50-56, 63.

ZHANG Wenxiu, WU Xinfang. Research on condition monitoring and fault diagnosis technology of wind turbines[J].ElectricMachines&ControlApplication, 2014, 41(2): 50-56, 63.

[2] YANG Wenxian, JIANG Jiesheng, TAVNER P J, et al. Monitoring wind turbine condition by the approach of empirical mode decomposition[C]//Proceedingsof2008InternationalConferenceonElectricalMachinesandSystems. Wuhan, China: IEEE, 2008: 736-740.

[3] 龍泉, 劉永前, 楊勇平. 狀態監測與故障診斷在風電機組上的應用[J].現代電力, 2008, 25(6): 55-59.

LONG Quan, LIU Yongqian, YANG Yongping. Applications of condition monitoring and fault diagnosis to wind turbines[J].ModernElectricPower, 2008, 25(6): 55-59.

[4] 許小剛, 王松嶺, 劉錦廉. 基于小波包能量分析及改進支持向量機的風機機械故障診斷[J].動力工程學報, 2013, 33(8): 606-612.

XU Xiaogang, WANG Songling, LIU Jinlian. Mechanical fault diagnosis of fan based on wavelet packet energy analysis and improved support vector machine[J].JournalofChineseSocietyofPowerEngineering, 2013, 33(8): 606-612.

[5] 彭華東, 陳曉清, 任明, 等. 風電機組故障智能診斷技術及系統研究[J].電網與清潔能源, 2011, 27(2): 61-66, 70.

PENG Huadong, CHEN Xiaoqing, REN Ming, et al. Intelligent fault diagnosis technology and system for wind turbines[J].PowerSystemandCleanEnergy, 2011, 27(2): 61-66, 70.

[6] 陳宏, 袁浩東, 張帥偉, 等. 基于振動能量的設備狀態評價方法研究[J].機械設計與制造, 2013(2): 127-130.

CHEN Hong, YUAN Haodong, ZHANG Shuaiwei, et al. Research on the condition assessment method of equipment based on vibration energy[J].MachineryDesign&Manufacture, 2013(2): 127-130.

[7] 陳釗, 任瑞冬, 符嬈. 一種基于時域濾波算法的振動信號有效值計算方法研究[J].現代機械, 2015(3): 52-55.

CHEN Zhao, REN Ruidong, FU Rao. A research of vibration signal RMS value calculation based on time-domain filtering altorithm[J].ModernMachinery, 2015(3): 52-55.

[8] 孫立明, 單服兵, 朱孔敏, 等. 軸承振動、噪聲與振動峰值和波峰因數關系[J].洛陽工學院學報, 2002, 23(1): 65-70.

SUN Liming, SHAN Fubing, ZHU Kongmin, et al. The relation of vibration peak and crest factor with vibration and noise of the deep groove ball bearing[J].JournalofLuoyangInstituteofTechnology, 2002, 23(1): 65-70.