一種基于流形正則化的半監(jiān)督指紋定位算法
朱順濤,盧先領(lǐng),于丹石
(1. 江南大學(xué)“輕工過程先進(jìn)控制”教育部重點(diǎn)實驗室,江蘇 無錫 214100; 2. 江南大學(xué)物聯(lián)網(wǎng)工程學(xué)院,江蘇 無錫 214100)
近年來,隨著人們對于室內(nèi)位置服務(wù)的需求日益迫切,室內(nèi)定位技術(shù)受到廣泛關(guān)注[1-3]。其中基于WLAN的室內(nèi)指紋定位方位法憑借易部署、精度高、非視距等優(yōu)點(diǎn),逐步成為室內(nèi)定位技術(shù)中研究的熱點(diǎn)[4-5]。該方法主要分為離線訓(xùn)練和在線定位兩個階段[6]。離線訓(xùn)練階段的主要工作是在每個參考點(diǎn)處采集一定數(shù)量的接收信號強(qiáng)度(received signal strength,RSS)信息,構(gòu)建位置指紋數(shù)據(jù)庫,并利用機(jī)器學(xué)習(xí)算法構(gòu)建定位模型;在線定位階段則根據(jù)待定位點(diǎn)處測得的RSS及離線階段訓(xùn)練好的定位模型進(jìn)行位置估計。
國內(nèi)外學(xué)者提出幾種典型的室內(nèi)指紋定位算法。文獻(xiàn)[7]提出一種改進(jìn)的神經(jīng)網(wǎng)絡(luò)(improved neural network,INN)指紋定位算法,該算法結(jié)合神經(jīng)網(wǎng)絡(luò)初始參數(shù)設(shè)置與均方誤差之間的相關(guān)性,來訓(xùn)練獲得RSS指紋和位置坐標(biāo)之間復(fù)雜的映射關(guān)系;文獻(xiàn)[8]提出一種基于支持向量回歸(support vector regression,SVR)的室內(nèi)定位算法,該算法利用支持向量回歸得到位置預(yù)測模型,提高定位精度的同時降低了對存儲容量及計算能力的要求。文獻(xiàn)[9]將極限學(xué)習(xí)機(jī)(extreme learning machine,ELM)運(yùn)用到位置指紋定位算法中,憑借ELM隨機(jī)特征映射的特點(diǎn)獲得極快的學(xué)習(xí)速度,減少了離線學(xué)習(xí)時間;另外,ELM有著緊密的網(wǎng)絡(luò)結(jié)構(gòu),能有效克服環(huán)境變化以及RSS時變性對定位精度的影響。傳統(tǒng)指紋定位算法離線階段都需要采集大量帶有位置標(biāo)簽的訓(xùn)練數(shù)據(jù)來確保定位精度,這一過程將會耗費(fèi)大量的人力物力,而大量無標(biāo)簽的指紋數(shù)據(jù)則可以通過定位區(qū)域中的移動終端輕松采集[10]。因此,充分利用帶標(biāo)簽和無標(biāo)簽數(shù)據(jù)的半監(jiān)督指紋算法有利于降低室內(nèi)指紋定位算法對帶標(biāo)簽位置數(shù)據(jù)的需求[11]。
針對傳統(tǒng)指紋定位算法采集帶標(biāo)簽訓(xùn)練數(shù)據(jù)成本高的問題,本文提出一種基于流形正則化的半監(jiān)督指紋定位算法。
1 極限學(xué)習(xí)機(jī)
極限學(xué)習(xí)機(jī)(extreme learning machine,ELM)[12]是由Huang等提出的一種單隱含層前饋神經(jīng)網(wǎng)絡(luò)算法。該算法摒棄了梯度下降算法的迭代調(diào)整策略,通過隨機(jī)產(chǎn)生隱含層的輸入權(quán)值和偏移量來計算相應(yīng)的輸出權(quán)值矩陣,在保證學(xué)習(xí)精度的前提下比傳統(tǒng)的學(xué)習(xí)算法速度更快。ELM的基本網(wǎng)絡(luò)結(jié)構(gòu)如圖1所示。
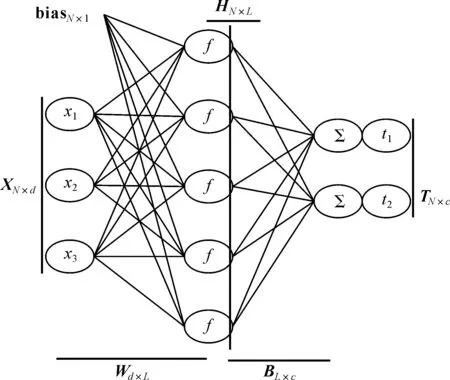
圖1 ELM算法的網(wǎng)絡(luò)結(jié)構(gòu)
對于任意N個訓(xùn)練樣本集{(xj,tj)}j=1,2,…,N,ELM回歸模型為
(1)
式中,ωi是連接輸入節(jié)點(diǎn)和第i個隱含層節(jié)點(diǎn)之間的權(quán)值;bi是第i個隱含層節(jié)點(diǎn)的偏移量;g()是激活函數(shù);βi是第i個隱含層節(jié)點(diǎn)輸出權(quán)值;L是隱含層節(jié)點(diǎn)個數(shù)。將式(1)寫成矩陣形式為
Hβ=T
(2)
式中,隱含層輸出矩陣、位置輸出矩陣及輸出權(quán)值矩陣分別為
(3)
T=[t1t2…tN]T,β=[β1β2…βL]T
(4)
ELM模型通過最小化訓(xùn)練誤差函數(shù)及輸出權(quán)值矩陣的模,來計算隱含層的輸出權(quán)值矩陣,從而完成相應(yīng)模型的構(gòu)建。ELM的目標(biāo)函數(shù)可表示為[13]
(5)
式中,e是誤差向量;C是訓(xùn)練誤差懲罰系數(shù)矩陣。
2 流形正則化極限學(xué)習(xí)機(jī)
2.1 流形正則化框架
流形正則化(manifold regularization,MR)是一種通過構(gòu)建無向有權(quán)圖及圖拉普拉斯算子來進(jìn)行半監(jiān)督學(xué)習(xí)的方法[14],其通過整合流行正則化方法從而將那些未標(biāo)記樣本用于模型的訓(xùn)練。該方法建立在流形假設(shè)基礎(chǔ)之上,流形假設(shè)可概括為:假設(shè)所有樣本處于一個很小的局部鄰域,那么它們就應(yīng)該具有相近的標(biāo)記[15]。用數(shù)學(xué)語言表達(dá)如下:如果x1和x2在同一個局部鄰域內(nèi),那么x1的條件概率P(y|x1)和x2的條件概率P(y|x2)也應(yīng)該相近。
給定一個訓(xùn)練樣本集,其中包括l個標(biāo)記樣本{(xi,ti)}(i=1,2,…,l)和u個未標(biāo)記樣本{xi}(i=1,2,…,u),流形正則化框架的最小化成本函數(shù)Lm為
(6)
式中,Wij為樣本點(diǎn)xi和xj之間的邊權(quán)值矩陣,計算方式如下
(7)
式中,KNN(xj)表示xj的最近鄰點(diǎn)集合。由于條件概率不容易求得,可將式(6)簡化為
(8)
根據(jù)圖譜理論,式(8)能進(jìn)一步寫為如下形式
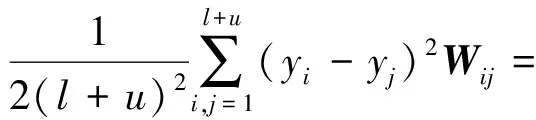
(9)

2.2 流形正則化框架和極限學(xué)習(xí)機(jī)的融合算法
本節(jié)將流形正則化和極限學(xué)習(xí)機(jī)相結(jié)合,提出一種基于流形正則化的半監(jiān)督指紋定位算法(manifold regularization extreme learning machine,MR-ELM),充分利用大量無標(biāo)簽數(shù)據(jù),減少采集帶標(biāo)簽數(shù)據(jù)的工作量,同時繼承了極限學(xué)習(xí)機(jī)無需迭代、模型執(zhí)行高效的優(yōu)點(diǎn)。
具體過程是將式(9)表示的流形結(jié)構(gòu)作為懲罰項來約束式(5)中的ELM目標(biāo)函數(shù),則MR-ELM算法的目標(biāo)函數(shù)表現(xiàn)形式為
(10)

(11)
式中,L表示在帶標(biāo)簽數(shù)據(jù)和無標(biāo)簽數(shù)據(jù)空間中建立的圖拉普拉斯算子;F表示經(jīng)模型運(yùn)算后的輸出矩陣;L是隱含層節(jié)點(diǎn)個數(shù);no是輸出層節(jié)點(diǎn)個數(shù)。
當(dāng)利用K近鄰方法構(gòu)建鄰接圖時,權(quán)重矩陣計算如式(7)所示,該方法雖然減少了計算量,便于實現(xiàn),但是節(jié)點(diǎn)的位置預(yù)測更偏向于它鄰居節(jié)點(diǎn)的位置,從而降低了預(yù)測精度。為了解決這個問題,引入高斯核函數(shù)進(jìn)行權(quán)重矩陣計算[16],從而更好地反映樣本空間的流形,提高預(yù)測精度,公式如下
(12)
將式(10)約束因子代入目標(biāo)函數(shù),則MR-ELM目標(biāo)函數(shù)的矩陣形式可簡寫為
(13)
將式(13)對β求導(dǎo),并令其等于0,得
(14)
當(dāng)帶標(biāo)簽數(shù)據(jù)的個數(shù)大于隱含層節(jié)點(diǎn)的個數(shù)時
β=(IL+HTCH+λHTLH)-1HTCY
(15)
當(dāng)帶標(biāo)簽數(shù)據(jù)的個數(shù)小于隱含層節(jié)點(diǎn)的個數(shù)時
β=HT(Il+u+CHHT+λLHHT)-1CY
(16)
式中,I是單位矩陣;懲罰矩陣C=diag(1,1,…,0,0)。通過求解β得到訓(xùn)練好的MR-ELM定位模型。
3 仿真結(jié)果分析
本文通過計算機(jī)模擬簡化場景下的射線跟蹤,生成仿真環(huán)境下的指紋數(shù)據(jù)庫(數(shù)據(jù)來源:https:∥github.com/jiangqideng/codeInBlogs/tree/master/IP_raytracing)。該指紋庫的覆蓋范圍為20 m×15 m的矩形區(qū)域,有6個AP節(jié)點(diǎn)。試驗收集30 000條訓(xùn)練數(shù)據(jù)和10 000條測試數(shù)據(jù),其中訓(xùn)練數(shù)據(jù)包括帶標(biāo)簽數(shù)據(jù)和無標(biāo)簽數(shù)據(jù)。指紋數(shù)據(jù)庫中的數(shù)據(jù)形式見表1,接收信號強(qiáng)度作為輸入特征向量,位置坐標(biāo)作為輸出特征向量。系統(tǒng)的運(yùn)行軟件環(huán)境為Matlab 2012b,硬件環(huán)境為Core i3、3.7 GHz、8 GB內(nèi)存的PC機(jī)。

表1 部分訓(xùn)練數(shù)據(jù) dBm
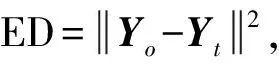
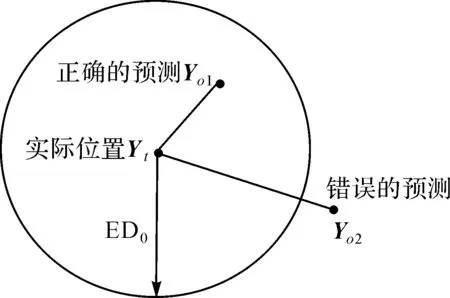
圖2 誤差距離定義
如圖3所示,隨著帶標(biāo)簽訓(xùn)練數(shù)據(jù)個數(shù)的增加,4種算法的平均定位誤差逐漸下降并趨于穩(wěn)定,這是由于帶標(biāo)簽訓(xùn)練數(shù)據(jù)中所包含的信息改善了學(xué)習(xí)的性能,提高了定位精度。當(dāng)帶標(biāo)簽訓(xùn)練個數(shù)達(dá)到12 000時,MR-ELM算法的平均定位誤差在1.5 m左右,相比于INN、SVR和ELM算法,分別降低了31.70%、24.90%和10.84%。

圖3 各算法平均定位誤差比較
假設(shè)誤差距離為2 m,在不同帶標(biāo)簽數(shù)據(jù)個數(shù)的情況下,對4種算法的定位準(zhǔn)確率進(jìn)行統(tǒng)計。如圖4所示,MR-ELM算法的定位準(zhǔn)確率高于其他3種算法,尤其是當(dāng)帶標(biāo)簽訓(xùn)練數(shù)據(jù)的個數(shù)小于12 000的稀疏狀態(tài)時。當(dāng)N=3000時,MR-ELM的定位準(zhǔn)確率與INN、SVR、ELM算法相比,分別提高了33.52%、4.67%和16.56%。
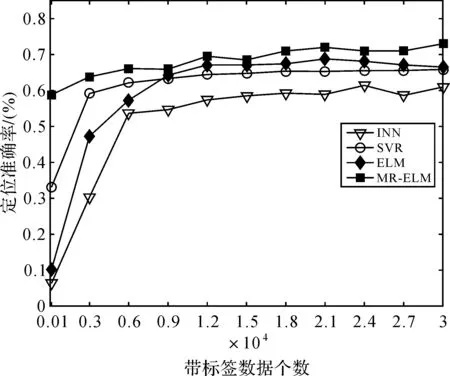
圖4 各算法定位準(zhǔn)確率比較圖
圖5反映了帶標(biāo)簽訓(xùn)練數(shù)據(jù)個數(shù)與訓(xùn)練時間之間的關(guān)系,可以看出隨著帶標(biāo)簽訓(xùn)練數(shù)據(jù)的不斷增加,INN、SVR算法所需的訓(xùn)練時間增長較快,而ELM和MR-ELM兩種算法的訓(xùn)練時間僅小幅增加。MR-ELM算法的訓(xùn)練時間略高于ELM算法,這是因為其在處理帶標(biāo)簽訓(xùn)練數(shù)據(jù)的同時,還需處理無標(biāo)簽數(shù)據(jù)。表2為4種算法在帶標(biāo)簽數(shù)據(jù)個數(shù)為3000,訓(xùn)練時間和測試時間的比較。可知,MR-ELM算法所需的訓(xùn)練時間和測試時間分別為2.50和0.05 s,符合實際定位要求。
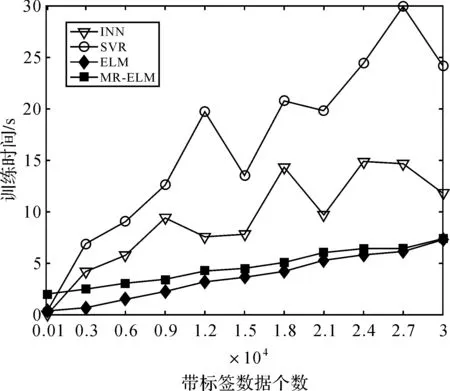
圖5 各算法離線階段訓(xùn)練時間比較圖
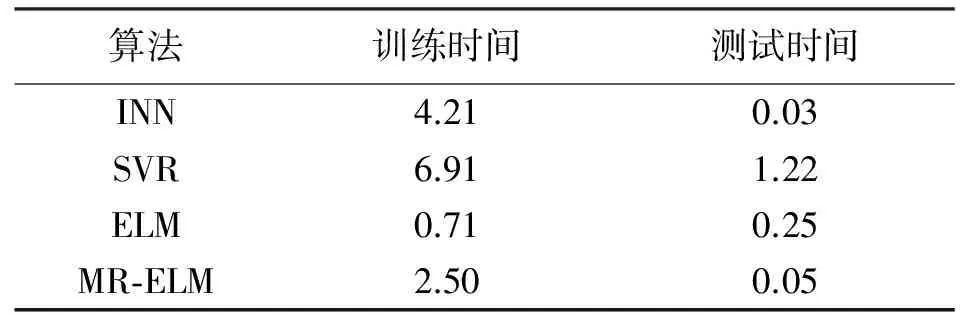
s
為了驗證MR-ELM算法在帶標(biāo)簽訓(xùn)練數(shù)據(jù)稀疏情況下定位效果的穩(wěn)定性,試驗將帶標(biāo)簽訓(xùn)練個數(shù)和距離誤差作為條件,對各算法的定位準(zhǔn)確率進(jìn)行了統(tǒng)計。試驗結(jié)果如圖6所示,MR-ELM算法在N=100、3000、6000、9000的4種帶標(biāo)簽訓(xùn)練數(shù)據(jù)較少的情況,定位的準(zhǔn)確率更高,且隨著帶標(biāo)簽訓(xùn)練數(shù)據(jù)的減少,MR-ELM算法的定位準(zhǔn)確率的波動性遠(yuǎn)小于其他3種算法。
4 結(jié) 語
本文提出了一種基于流形正則化的半監(jiān)督指紋定位算法。該算法首先以流形假設(shè)為依據(jù),利用批量輸入的帶標(biāo)簽數(shù)據(jù)與無標(biāo)簽數(shù)據(jù)之間的相似度構(gòu)建圖拉普拉斯算子;然后與極限學(xué)習(xí)機(jī)算法相結(jié)合,通過隨機(jī)特征映射建立隱含層;最后在流形正則化框架下,求解隱含層和輸出層之間的權(quán)值矩陣,從而建立接收信號強(qiáng)度與位置之間的映射關(guān)系,即位置估計模型。仿真結(jié)果表明,與INN、SVR、ELM 3種算法相比,該算法的訓(xùn)練和測試時間較短,且在帶標(biāo)簽訓(xùn)練數(shù)據(jù)稀疏的前提下仍能保持較高的準(zhǔn)確率與穩(wěn)定性。
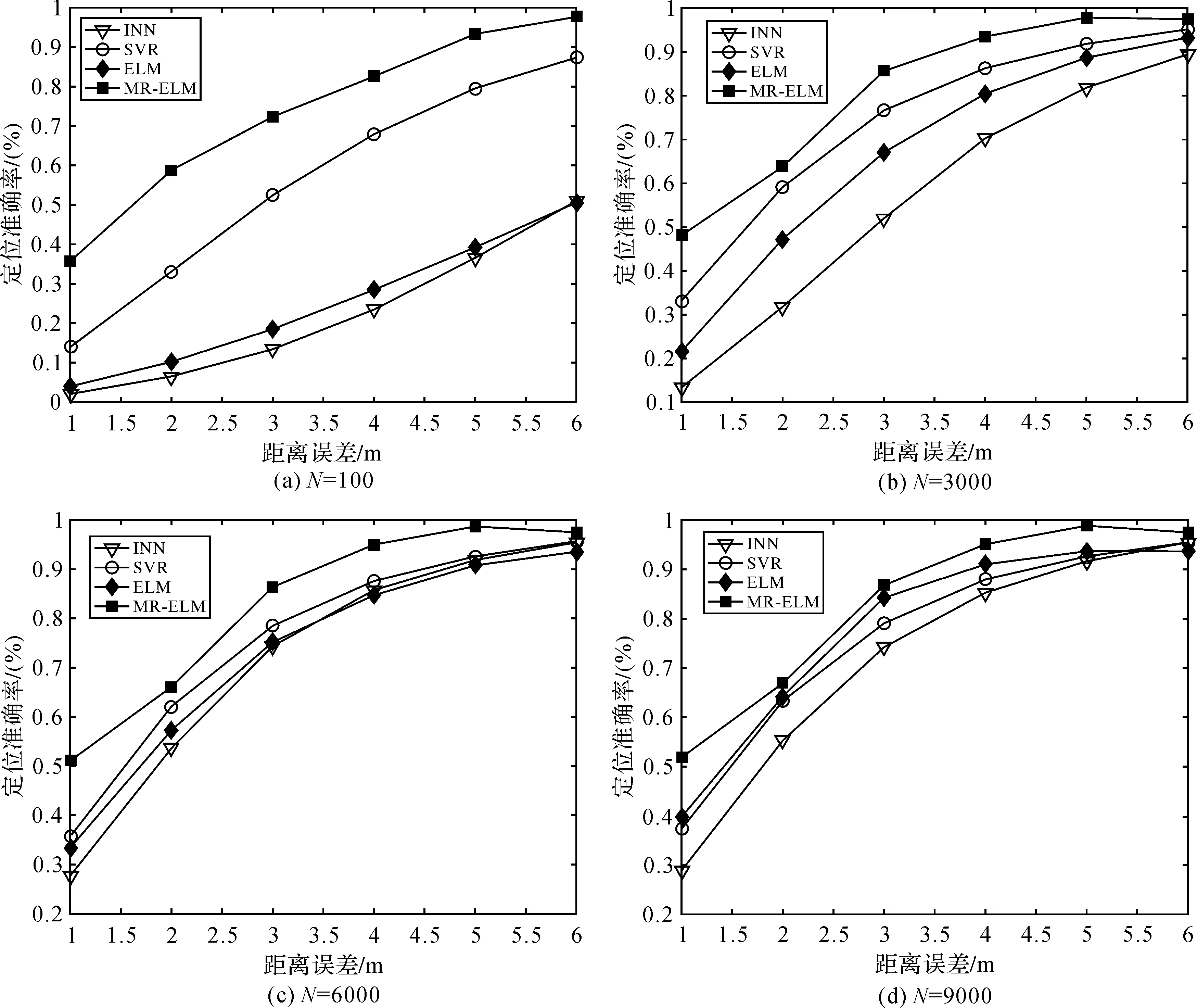
圖6 不同帶標(biāo)簽訓(xùn)練數(shù)據(jù)和距離誤差情況下定位準(zhǔn)確率比較
隨著時間的推移、室內(nèi)環(huán)境的改變,在參考點(diǎn)處接收到的指紋信號將會發(fā)生變化,導(dǎo)致定位模型精度的降低,今后的研究重點(diǎn)是進(jìn)一步提高定位模型對動態(tài)環(huán)境的適應(yīng)能力。
[1] DENG Zhongliang,YU Yanpei,YUAN Xie,et al.Situation and Development Tendency of Indoor Positioning[J].China Communication,2013,10(3): 42-55.
[2] 靳超,邱冬煒.基于WiFi信號室內(nèi)定位技術(shù)的研究[J].測繪通報,2017(5): 21-25.
[3] 畢京學(xué),甄杰,汪云甲,等.高斯函數(shù)定權(quán)的改進(jìn)KNN室內(nèi)定位方法[J].測繪通報,2017(6):9-12.
[4] HE S,CHAN S H G.Wi-Fi Fingerprint-based Indoor Positioning: Recent Advances and Comparisons[J].IEEE Communications Surveys & Tutorials,2016,18(1):466-490.
[5] 崔斌,趙西安.一種基于傳播模型和位置指紋的混合室內(nèi)定位方法[J].測繪通報,2015(6): 35-43.
[6] XIA S,LIU Y,Yuan G,et al.Indoor Fingerprint Positioning Based on Wi-Fi: An Overview[J].International Journal of Geo-Information,2017,6(5):135.
[7] MOK E,CHEUNG B K S.An Improved Neural Network Training Algorithm for Wi-Fi Fingerprinting Positioning[J].ISPRS International Journal of Geo-Information,2013,2(3):854-868.
[8] SHI K,CHEN H S,ZHANG R T.Indoor Location Method Based on Support Vector Regression in 802.11 Wireless Rnvironments[J].Journal of Software,2014,25(11): 2636-2651.
[9] DWIYASA F,LIM M H,ONG Y S,et al.Extreme Learning Machine for Indoor Location Fingerprinting[J].Multidimensional Systems & Signal Processing,2017,28(3):867-883.
[10] 向銘.基于半監(jiān)督學(xué)習(xí)的室內(nèi)WLAN支持向量回歸定位算法[D].重慶:重慶郵電大學(xué),2016.
[11] PULKKINEN T,ROOS T,MYLLYMKI P.Semi-supervised Learning for WLAN Positioning[C]∥Proceedings of the 21th International Conference on Artificial Neural Networks and Machine Learning.Espoo:Springer-Verlag,2011.
[12] HUANG G B,ZHOU H,DING X,et al.Extreme Learning Machine for Regression and Multiclass Classification[J].IEEE Transactions on Systems,Man and Cybernetics,2012,42(2):513-529.
[13] LU X,ZOU H,ZHOU H,et al.Robust Extreme Learning Machine With its Application to Indoor Positioning[J].IEEE Transactions on Cybernetics,2016,46(1):194-205.
[14] NIYOGI P,Manifold Regularization and Semi-supervised Learning:Some Theoretical Analyses [J].Journal of Machine Learning Research,2013,14(1): 1229-1250.
[15] BELKIN M,NIYOGI P,SINDHWANI V.Manifold Regularization: A Geometric Framework for Learning from Labeled and Unlabeled Examples[J].Journal of Machine Learning Research,2006,7(1): 2399-2434.
[16] 陶新民,曹盼東,宋少宇,等.基于半監(jiān)督高斯混合模型核的支持向量機(jī)分類算法[J].信息與控制,2013,42(1):18-26.

