一種相機標定輔助的單目視覺室內定位方法

王 勇，陳國良，李曉園，田 鵬,4，周 雨

(1. 中國礦業大學機電工程學院，江蘇 徐州 221000; 2. 徐州市產品質量監督檢驗中心，江蘇 徐州 221000; 3. 中國礦業大學環境與測繪學院，江蘇 徐州 221000; 4. 徐州市勘察測繪研究院，江蘇 徐州 221000)

隨著社會的發展、國防建設的需要，以及人們需求的增長，基于位置的服務成為研究的熱點。如何在復雜環境中快速獲取準確的位置，便于在緊急救助、醫療服務、信息傳遞等鄰域發揮巨大的作用成為至關重要的問題。對于現代導航定位來說，室內由于建筑物的遮擋，GPS接收機很難收到衛星的信號。因此，WiFi[1-3]、白光[4]、可見光[5]、超寬帶(UWB)[6]、行人航跡推算(PDR)[7]、藍牙的各種室內定位技術應運而生，各種基于人工智能和傳感器融合的算法實現了優于1 m精度的室內定位[8-10]。

研究發現上述室內定位方法都需要在室內環境附加安裝一些電子裝置才能實現，本文以公共場所常見的監控攝像裝置采集的實時視頻流為基礎，實現了一種利用視頻序列和多區域分割的室內定位方法，無需任何現場附加裝置，實現高精度的室內定位。具體的實現步驟如圖1所示，首先對不同的平面進行相機標定，獲取投影矩陣；然后對視頻序列中的目標進行檢測，獲取目標的像素坐標；最后結合投影矩陣與像素坐標進行空間坐標的解算，完成對室內目標的定位。

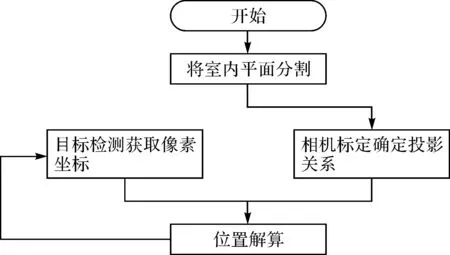
圖1 定位流程

1 相機標定

相機標定是從二維像片中獲取三維尺度信息必不可少的步驟，對三維計算機視覺尤為重要。通過相機標定可以獲取像片中像素與空間物體的映射關系，從而達到利用像素坐標解算空間坐標的目的。本文選用文獻[11]中的張正友標定法進行相機的標定。

1.1 相機成像模型

相機標定采用針孔模型作為相機成像模型，根據針孔成像模型可以得到如下的映射關系

(1)

式中，u、v為P點的像素坐標；X、Y、Z為P點的空間坐標；s為尺度因子；r1、r2、r3為旋轉參數，t為平移參數，統稱為相機的外參；A為相機的內參矩陣。

式(1)是空間坐標與像素坐標間的映射關系，張正友標定法中假設標定板的平面為0，即Z=0，因此式(1)可以簡化為式(2)，通過對式(2)中的相應參數進行解算可完成相機標定。

(2)

1.2 相機內外參數的解算

相機成像模型建立好之后就需要對相機的內外參數進行求解得到像素坐標與空間坐標之間的轉化關系。張正友標定法用于相機內外參數的求解過程如圖2所示。

1.2.1 單應矩陣求解

式(1)可以化簡為

sm=HM

(3)

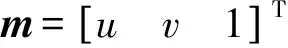
式中，X=H。

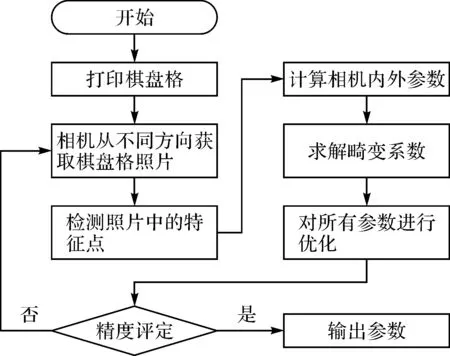
圖2 張正友相機標定步驟

1.2.2 內外參數求解

結合式(2)和式(3)，可以得到

(4)

式中，λ=1/s，由旋轉矩陣的正交性可以得到如下兩式

(5)

(6)

式(5)、式(6)又可以寫成矩陣的形式

(7)

最后通過對式(7)求解的b進行分解后就可以求出相機的內外參數，具體求解過程可以參考文獻[12]，這里不再贅述。

1.2.3 相機的畸變參數求解

通過式(7)計算出來的相機內外參數是在針孔成像模型的前提下解算的。實際上相機在成像過程中會出現畸變，因此還需要求解相機的畸變參數。相機的畸變有3種模式，分別為徑向畸變、離心畸變、薄棱鏡畸變。考慮到徑向畸變為主要類型，因此只求解到二階徑向畸變參數[13]。徑向畸變參數通過下式求解

(8)

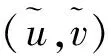
k=(DTD)-1DTd

(9)

2 運動目標檢測

運動目標檢測技術在智能監控領域發揮著重要的作用。本部分主要利用運動目標檢測技術獲取目標的像素坐標，為下一步目標空間位置的解算作準備。目前常用的運動目標檢測方法有幀差法、背景差法[14]和光流法[15]3種。由于單一算法都不能完整地檢測運動目標，因此出現了混合算法。文獻[16]融合背景差法、光流法及可分離的數學形態邊緣檢測法(SMED)，減少了背景噪音，增強了對光照變化的適應性，增強了算法的穩健性。本文利用文獻提取強角點特征，然后結合金字塔Lucas-Kanade(L-K)光流算法對目標進行檢測。金字塔L-K光流算法流程如圖3所示。

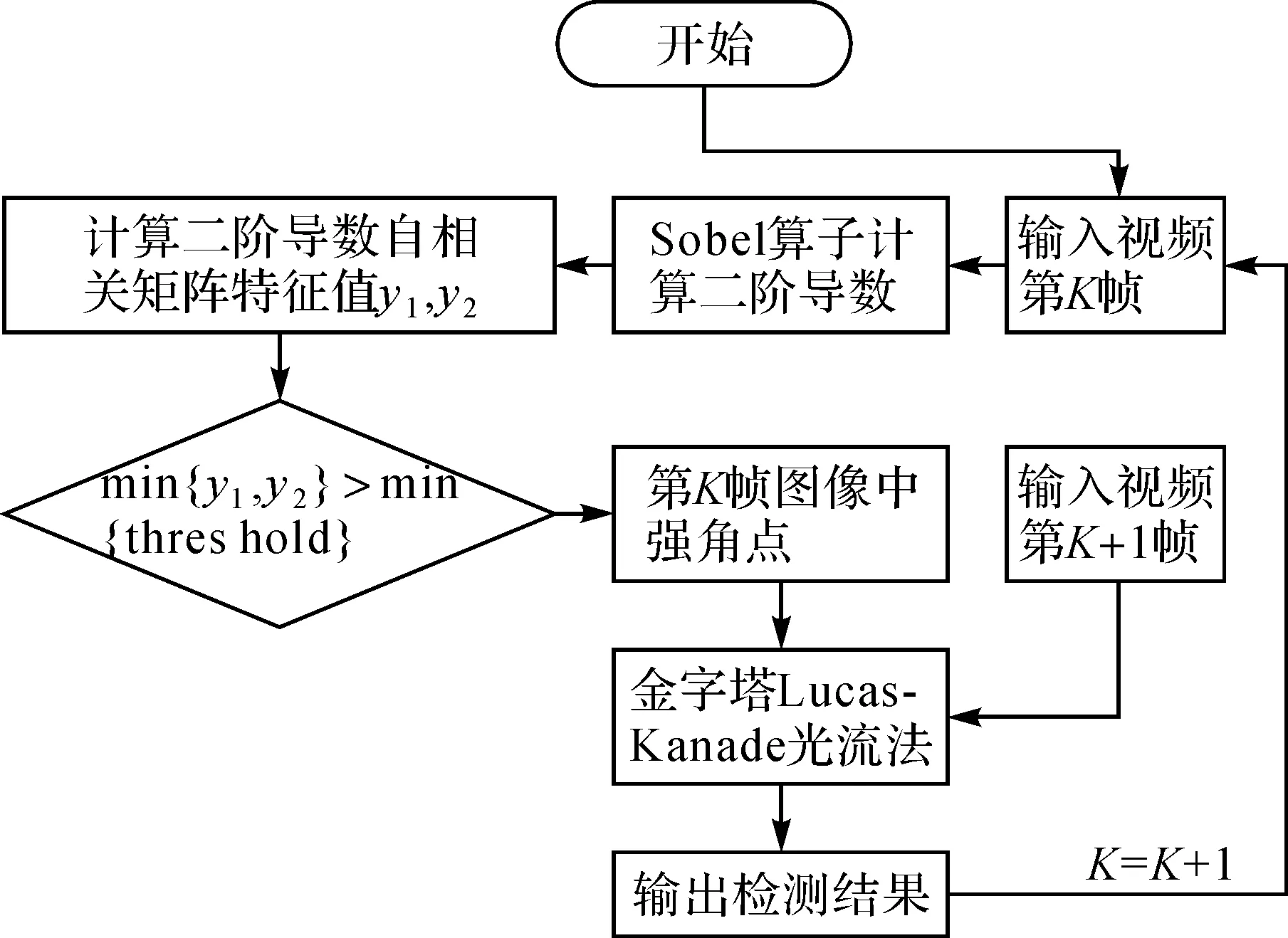
圖3 金字塔Lucas-Kanade光流算法流程

2.1 強角點提取

傳統的Lucas-Kanade光流法用于求解稠密光流，計算量較大，因此不能滿足實時性的要求。在此基礎上本文先在初始圖像中提取強角點，然后對提取的強角點進行跟蹤，減少了計算量。強角點提取的數學模型如下

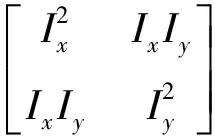
(10)

式中，w(x,y)為高斯函數；Ix為x方向偏導數；Iy為y方向偏導數；?表示卷積運算；M為二階導數的自相關矩陣。

由于M為二階矩陣，求解M矩陣的兩個特征值λ1、λ2。將兩個特征值與設定的閾值比較可以得到強角點，判斷準則需滿足

min{λ1,λ2}>min(threold)

(11)

2.2 結合強角點的金字塔Lucas-Kanade光流法

L-K光流法基于3個假設：①目標像素在幀間運動保持亮度恒定；②運動隨時間變化緩慢；③同一場景中同一表面上鄰近的點具有相似運動。在滿足上述3個條件后可以得到L-K光流法的數學模型如下

Ixu+Iyv+It=0

(12)

式中，Ix、Iy分別為圖像沿x、y方向的偏導數；It為圖像隨時間的導數；u、v分別為x、y方向的速度分量。通過上式可以看出，單個像素不能求解速度分量，因此需要利用鄰域像素一并解算

(13)

式中，n為鄰域窗口的大小。利用最小二乘法對式(13)進行求解就可以得到速度分量值。金字塔L-K算法是L-K算法的改進，其作用是克服了L-K算法只適用于小而連貫運動的缺陷，使其也能夠滿足大而不連貫的運動。

3 目標定位

相機標定獲取的像素坐標與空間坐標之間的映射關系可以表示為

(14)

展開并消去s后有

(15)

式(15)即為空間直線方程。從上式可以看出一個像素點對應射線上的任何一個空間點，因此不能通過單一像素坐標解算出空間坐標。從圖4中可以看出如果能夠得到平面Z的空間方程，結合式(15)就可以求得X、Y、Z的坐標。

假設平面Z的空間方程為Z=0，結合式(15)可以得出坐標求解方程為

該處樓房位于賈河河堤南側，影響道路鋪設和創森造林，對此，東明縣投入資金19萬元，由江蘇省鹽城市一專業樓房整體平移公司對樓房實施了平移，整棟樓房向東平移18米后，又向南平移了14米，為創森造林“讓道”。

(16)

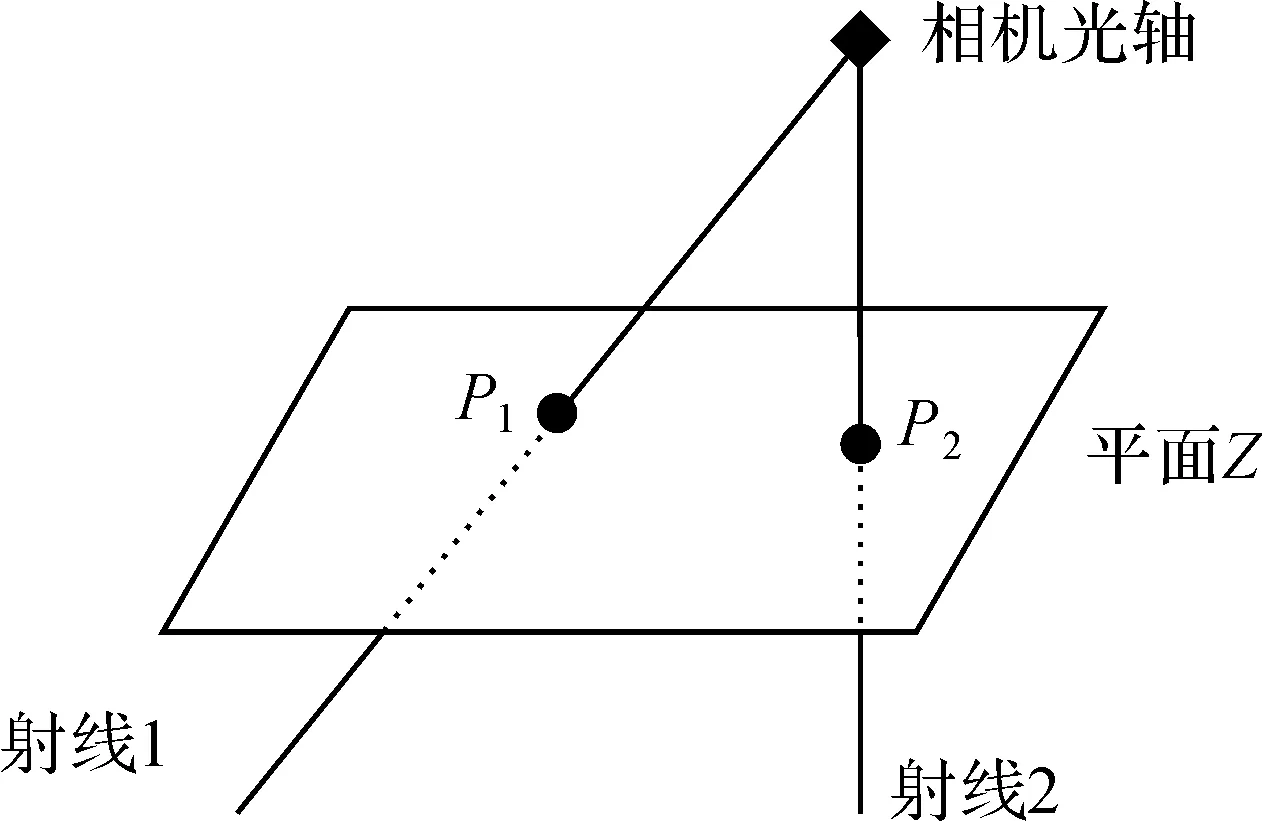
圖4 坐標解算模型

通過對上式進行求解，就可以利用目標物的像素坐標解算出空間坐標，實現目標定位。上述定位方法需要確定平面方程，因此本文將室內環境進行平面分割，針對不同的平面完成相機標定，確定平面方程，如圖5所示。

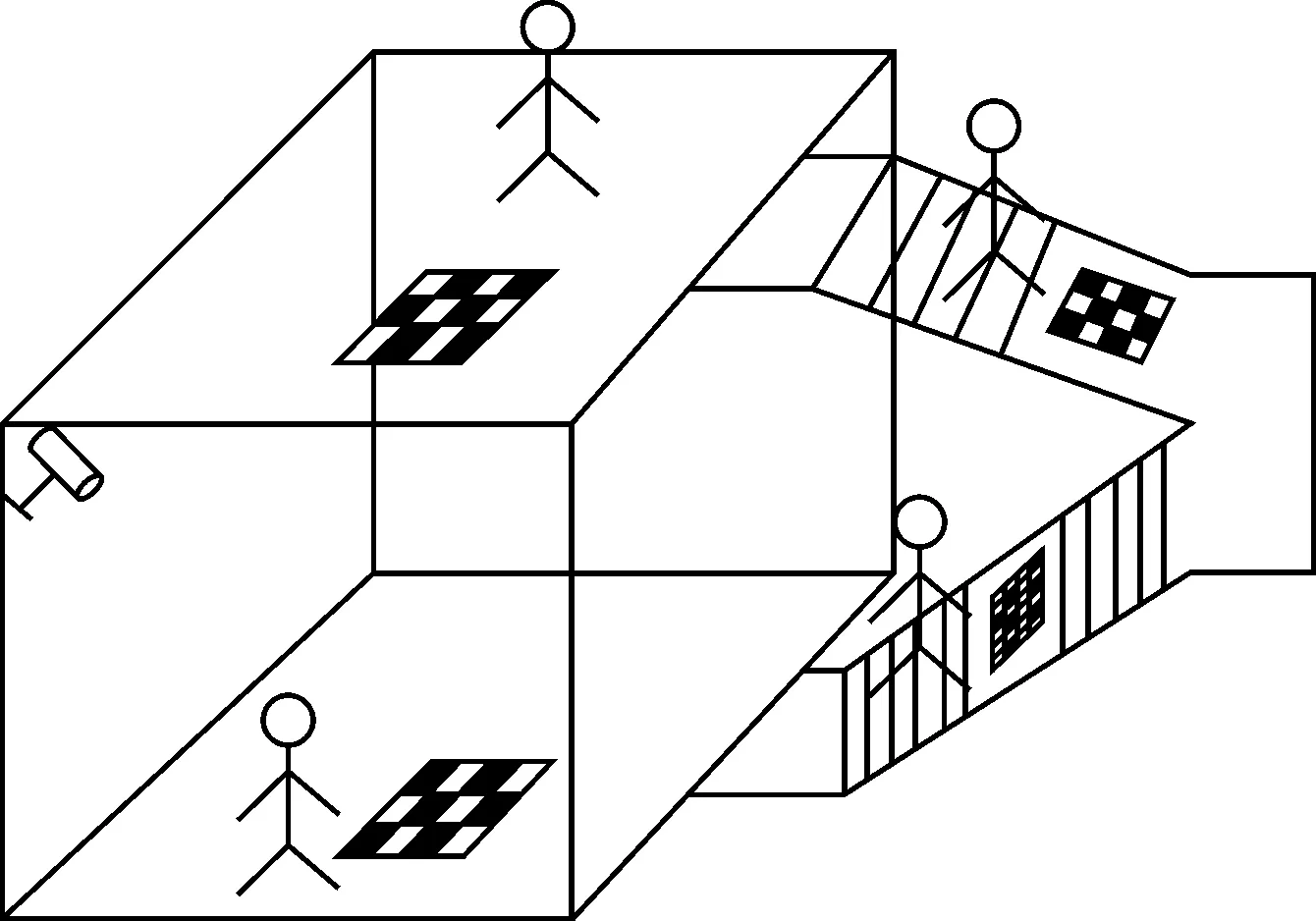
圖5 定位示意圖

4 試驗分析

4.1 試驗條件

試驗場所選用教學樓樓道和樓梯兩部分，試驗硬件平臺為智能手機及棋盤格標定板，軟件平臺為Opencv和Matlab。

4.2 相機標定

4.2.1 樓道平面標定結果

樓道平面選用17張棋盤格照片進行標定，如圖6所示。

圖6 樓道平面棋盤格標定

相機內參矩陣為

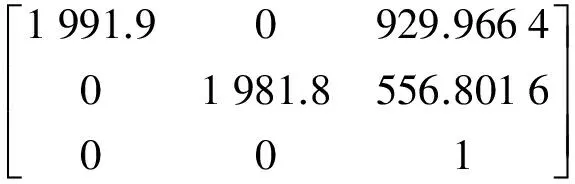
旋轉矩陣為

平移矩陣為

徑向畸變系數為

0.122 4 -0.067 6

由以上結果可以得到投影矩陣為

利用M矩陣就可實現圖像與空間的位置關系轉換。標定誤差如圖7所示。

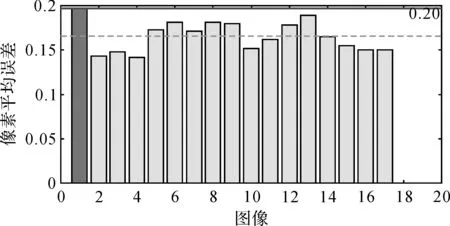
圖7 相機標定誤差(樓道平面)

從圖7可以看出，相機標定誤差小于0.2像素，標定結果達到了亞像素。

4.2.2 樓梯面標定結果

樓梯面標定使用14張棋盤格照片進行標定，如圖8、圖9所示。

圖8 樓梯平面棋盤格標定

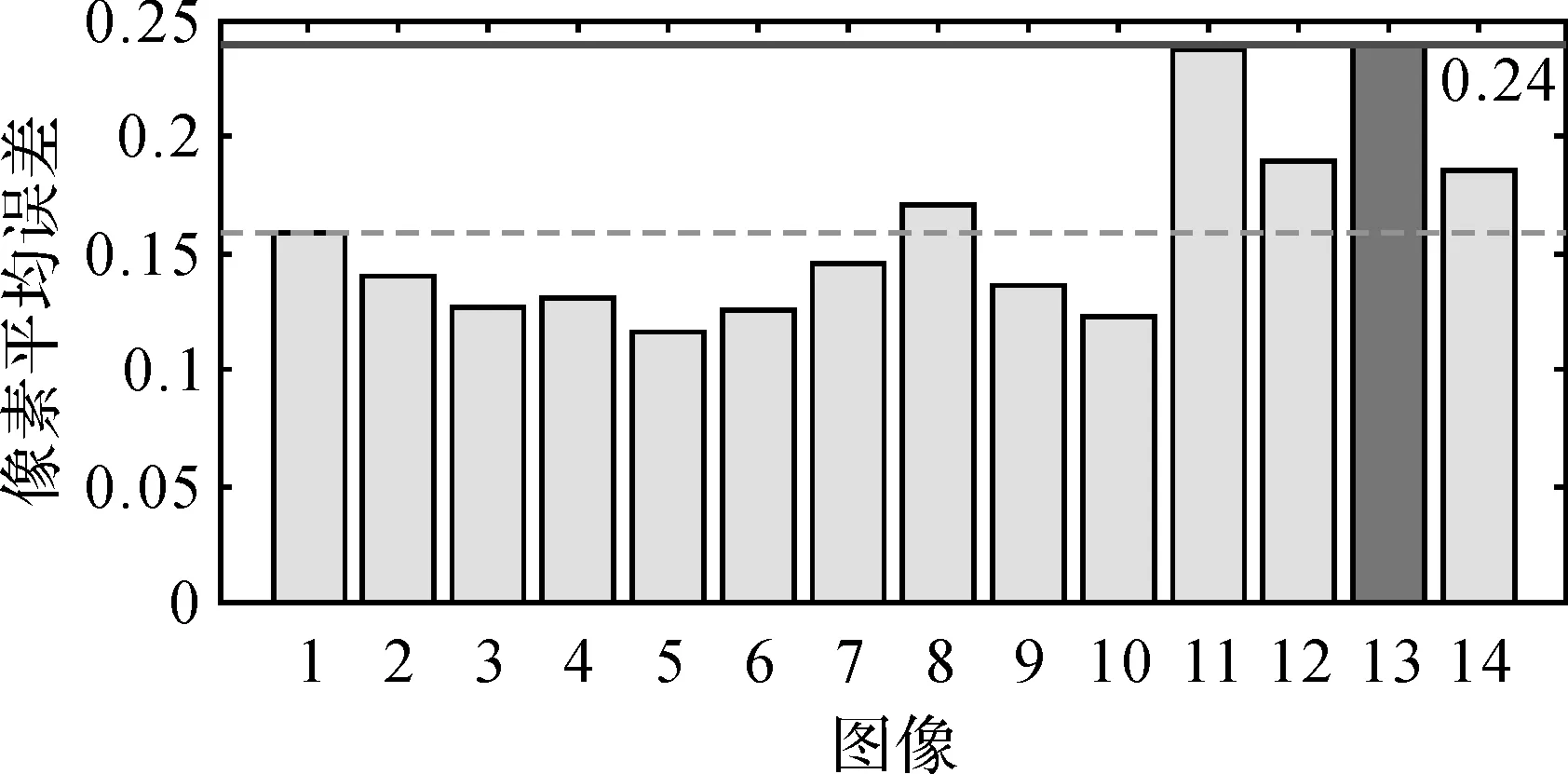
圖9 相機標定誤差(樓梯平面)

旋轉矩陣為

平移矩陣為

投影矩陣為

上面試驗分別對不同平面完成相機標定，得到了圖像坐標與空間位置的映射關系，標定結果精度達到了亞像素。

4.3 運動目標檢測

行人沿樓道平面和樓梯平面預先設置好的路線行走過程采集視頻，并采用金字塔L-K光流法進行了光流檢測。圖10(a)、圖10(b)分別為第155幀和200幀的原始圖像，圖10(c)、圖10(d)為其對應的光流檢測結果。

圖10 金字塔L-K光流法檢測

4.4 目標定位結果

行人沿樓道平面行走試驗的定位結果如圖11所示，最大定位誤差處為Y軸0.35 m，其余各處均小于0.1 m。行人沿樓梯行走試驗的定位結果如圖12所示，X、Y軸的誤差均小于0.1 m。

通過樓道平面和樓梯平面的試驗結果可以看出(如圖13所示)，本文提出的算法定位精度在X方向小于0.15 m，Y方向小于0.35 m，行人行走時在Y方向偏離真實軌跡較大，導致Y方向獲取的像素坐標誤差較大，因此Y方向誤差要大于X方向誤差；平均單點定位時間小于5 s，試驗結果達到了高精度、實時性的要求；畸變校正后軌跡與未校正的軌跡基本重合，表明本試驗所用相機鏡頭畸變尺度較小，對定位結果的影響可以忽略不計。

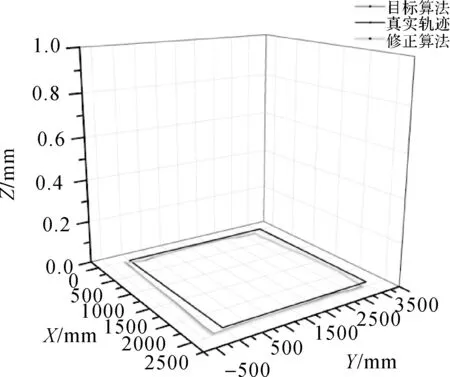
圖11 行人沿樓道平面行走定位結果

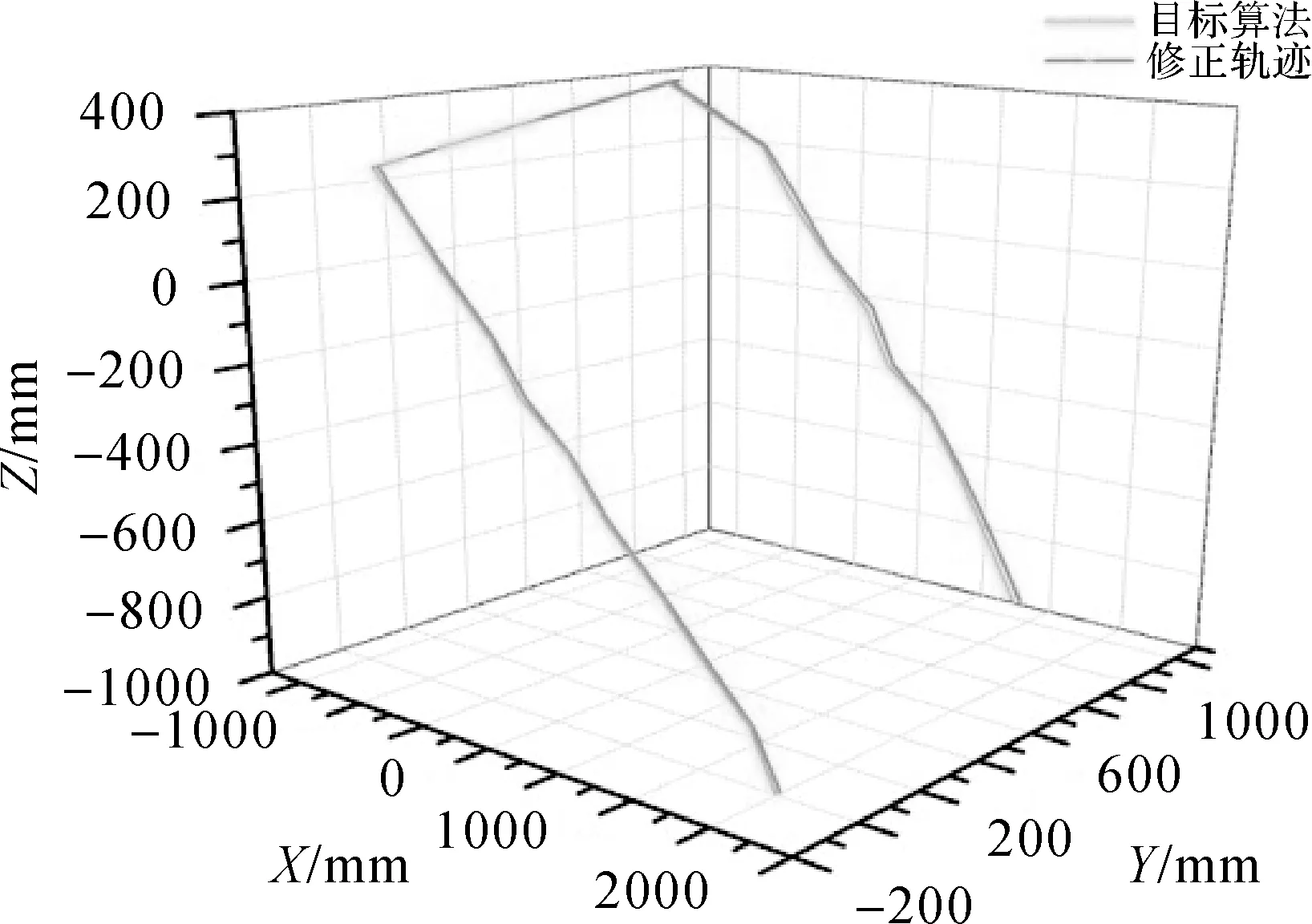
圖12 行人沿樓梯行走定位結果

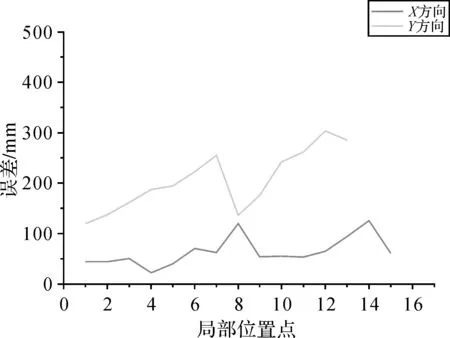
圖13 部分定位點沿X、Y方向定位誤差

5 結論與展望

本文將機器視覺技術應用在室內定位領域，通過對室內區域進行分割，結合相機標定和運動目標檢測技術實現對室內行人的高精度定位。試驗結果表明，定位精度小于0.5 m，均高于WiFi、藍牙等其他室內定位技術，可以滿足高精度室內定位的需求。由于室內攝像設備覆蓋范圍的限制，不能覆蓋所有的區域，但是可以通過與其他定位技術一起實現組合定位，完成覆蓋較大范圍內的定位需求。

[1] YANG Chouchang,SHAO Huairong.WiFi-based Indoor Positioning[J].IEEE Communications Magazine: Articles, News, and Events of Interest to Communications Engin-eers,2015,53(3):150-157.

[2] ZOU H, JIANG H, LU X, et al. An Online Sequential Extreme Learning Machine Approach to WiFi Based Indoor Positioning[C]∥ Internet of Things. [S.l.]: IEEE, 2014:111-116.

[3] TORTEEKA P, XIU C. Indoor Positioning Based on WiFi Fingerprint Technique Using Fuzzy K-nearest Neighbor[C]∥ International Bhurban Conference on Applied Sciences and Technology. [S.l.]: IEEE, 2014:461-465.

[4] NADEEM U, HASSAN N U, PASHA M A, et al. Highly Accurate 3D Wireless Indoor Positioning System Using White LED Lights[J]. Electronics Letters, 2014, 50(11):828-830.

[5] YASIR M, HO S W, VELLAMBI B N. Indoor Positioning System Using Visible Light and Accelerometer[J]. Journal of Lightwave Technology, 2014, 32(19):3306-3316.

[6] KOK M, HOL J D, SCHON T B. Indoor Positioning Using Ultrawideband and Inertial Measurements[J].IEEE Transactions on Vehicular Technology,2015,64(4):1293-1303.

[7] 陳國良,張言哲,汪云甲,等.WiFi-PDR室內組合定位的無跡卡爾曼濾波算法[J].測繪學報,2015,44(12):1314-1321.

[8] 張會清,石曉偉,鄧貴華,等.基于BP神經網絡和泰勒級數的室內定位算法研究[J].電子學報,2012,40(9):1876-1879.

[9] 李麗娜,馬俊,龍躍,等.基于LANDMARC與壓縮感知的雙段式室內定位算法[J].電子與信息學報,2016,38(7):1631-1637.

[10] TIAN Z, FANG X, ZHOU M, et al. Smartphone-based Indoor Integrated WiFi/MEMS Positioning Algorithm in a Multi-floor Environment[J]. Micromachines, 2015, 6(3):347-363.

[11] MORé J J. The Levenberg-marquardt algorithm: Implementa-tion and theory[J]. Lecture Notes in Mathematics, 1978, 630:105-116.

[12] ZHANG Z Y.A Flexible New Technique for Camera Calibration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(11):1330-1334.

[13] TSAI R Y. An Efficient and Accurate Camera Calibration Technique for 3D Machine Vision[J]. Proceeding of Computer Vision and Pattern Recognition, 1986(6):364-374.

[14] XU M, MA M. Real-time Detection of Moving Human Target under Indoor Environment Based on Video[C]∥ International Symposium on Test Automation & Instrumentation. Beijing:[s.n.],2014.

[15] LUCAS B D, KANADE T. An Iterative Image Registration Technique with an Application to Stereo Vision[C]∥ International Joint Conference on Artificial Intelligence. [S.l.]:Morgan Kaufmann Publishers,1981:674-679.

[16] SUGANYADEVI K, MALMURUGAN N. OFGM-SMED: An Efficient and Robust Foreground Object Detection in Compressed Video Sequences[M]. [S.l.]:Pergamon Press, 2014.