多面函數和移動法綜合模型支持下的區域垂直形變場擬合

田 曉，鄭洪艷，蘇廣利，王家慶

(中國地震局第一監測中心，天津 300180)

地殼垂直運動是地殼運動的一個重要分量，由于空間大地測量技術測定的高程分量精度低于水平分量，因此利用重復高精度水準測量仍然是目前研究地殼垂直運動的主要方法。但由于水準重合點是離散的，且水準網內部沒有數據，因此動態平差得到的垂直運動速率在時間域和空間域都是不連續的，實際上地殼垂直運動是一種連續的形態變化。為了實現在時空域內客觀準確地描述形變分布特征，往往需要基于離散的測點數據構建合適的數學模型擬合(最佳逼近)整個地區的地殼垂直形變速率面[1]。

在我國，從20世紀80年代末期開始，黃立人、趙承坤、楊國華和陶本藻等研究了多面函數擬合法在地殼垂直運動中的應用，幾位學者針對多面函數擬合中核函數的選擇、平滑因子的選擇及核函數中心點的選擇作了細致的研究，并提出了一系列獨特的見解[2-6]。劉經南等[7]研究了多面函數擬合法在建立我國地殼平面運動速度場模型中的應用。王文利等[8]利用多面函數擬合了我國陸地垂直運動速率圖。劉同文等[9]應用多面函數模型對西秦嶺地區的垂直形變速率作了研究和探討。秦姍蘭等[10]利用水準資料研究了西秦嶺地區的垂直形變，應用多面函數對區域整體形變特征進行擬合。

綜上所述，研究地殼垂直運動中，多面函數法是一種非常傳統并得到廣泛應用的方法，而其他方法應用并不多。本文應用多面函數和移動法綜合擬合模型，并以首都圈和晉冀蒙兩個地區的垂直運動為例，與其他幾種模型作對比研究。

1 模型方法數學原理

1.1 多面函數模型

多面函數模型是由美國Hardy教授于1977年提出的，并建議用于地殼垂直形變分析。該方法的基本思想為：任何數學表面和任何不規則的圓滑表面，總可以用一系列有規則的數學表面的和以任意精度逼近[9]。根據這一思想，假設地球表面上有一點(x,y)，其垂直速率值ξ(x,y)可以用下式來表示

(1)

式中，aj為待定系數；Qx,y,xj,yj是多面函數的核函數。核函數有多種類型，常用的有距離型核函數和錐面函數，其中距離型核函數表達式為

(2)

式中，δ為平滑因子，通常可取一小正數或0；μ一般取1/2、-1/2、3/2。當μ=1/2時，核函數稱為正雙曲面函數；當μ=-1/2時，核函數稱為倒雙曲面函數；當μ=3/2時，核函數稱為三次曲面函數。

錐面函數表達式為

(3)

式中，c為待定參數。

設有m個已知水準點xi,yi，選取其中n(n≤m)個點作為核函數的中心點xj,yj，令Qij=Q(xi,yi,xj,yj)，則各數據點應滿足

(4)

由此可列出誤差方程

V=QX-ξ

(5)

根據最小二乘原理可求得待定系數X，即

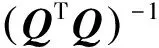
(6)

待定系數求出后，根據式(4)可計算測區各未知點的垂直形變速率值。

需要注意的是，應用多面函數擬合垂直形變速率時，要根據測區大小和地形情況確定合適的核函數、平滑因子和中心點個數。

1.2 移動曲面模型

移動曲面模型的基本原理是以每一個待定點為中心，選取待定點周圍適量的已知點，擬合出一個多項式曲面，進而內插出待定點上的函數值，是一種特殊的局部函數逼近法。

為了選取鄰近的數據點，以待定點Pxp,yp為圓心，以R為半徑作圓，凡落在圓內的數據點即被選用。應用時要根據實際情況選擇合適的半徑R。

定權時要根據已知點與待定點間的距離進行定權，常采用的權有以下幾種形式

在進行擬合前，可先將參與擬合的各點坐標進行中心化處理，即將各點坐標減去待定點P的坐標，這樣轉換后就變成以P為原點的坐標

(7)

(8)

最后求待定點P的垂直形變速率時，直接代入坐標0,0即可，從而在很大程度上方便了計算，而且有利于改善方程的數值穩定性和提高解算精度[11]。

1.3 多面函數和移動法加權綜合模型

該方法是基于綜合預報理論提出的，它并不是一種全新的方法，而是首先采用多面函數和移動法進行單獨擬合，然后對其擬合值進行加權綜合而得到最終擬合值[12]。用數學模型可表示為

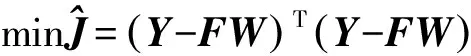
(9)

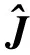
文獻[12]中并沒有給出該模型解的具體解法和表達式，本文給出W解的具體解法如下：

先構造拉格朗日極值函數

令

(10)

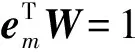
K=WTFTY-FW

(11)

另外，由式(10)可得

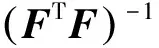
(12)

由式(11)和式(12)可采用迭代法解得W

(2) 將W0代入式(11)計算K。

(3) 將K代入式(12)計算W。

(4) 判斷W-W0<10-6,若是，退出循環；若否，令W0=W繼續重復步驟(2)—(4)。

經過以上迭代過程即可解得W為W*，則相應綜合模型擬合結果為

(13)

1.4 多面函數和移動法綜合擬合模型

多面函數法對整體性變化的擬合效果較好，但需要確定合適的模型參數，如果選取不當，容易出現擬合結果波動較大的現象，對局部變化擬合效果較差；而移動擬合法是以待定點為中心，以一定距離為半徑，用一個多項式曲面擬合待定點函數值的局部擬合法，具有較好的靈活性[13]。為此，可以結合兩者優點，采用先進行多面函數擬合，再對殘差進行移動法擬合的綜合模型擬合垂直形變速率。這很類似于組合法確定似大地水準面中的“移去—恢復”法，具體步驟如下：

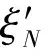
(2) 求出m個擬合點的速率擬合殘差v

v=ξN-ξ

(14)

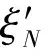
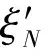
(15)

2 算例與分析

2.1 擬合方案介紹

本文選用首都圈地區2001年和2005年，以及晉冀蒙地區2002年和2006年各兩期水準數據進行研究，并對兩個地區的數據采用自由網平差法進行動態平差，計算垂直運動速率。兩段動態平差的單位權中誤差分別為1.03和1.15 mm/a，說明這兩個區域的數據整體實測精度比較好。剔除平差后速率中個別量值過大的突變點，首都圈地區共選用719個具有平差后速率的數據點(如圖1所示)，晉冀蒙地區共有627個具有平差后速率的數據點(如圖2所示)。由于對一個區域垂直形變場的擬合研究，主要為了得到未測點的垂直形變速率(即水準環內部區域的垂直形變速率)，因此為了更充分地得出結論，采用以下4種方案分別進行擬合計算：

方案1：均勻選取首都圈地區143個點作為外部檢核點(約占總點數的1/5)，其余576個點作為擬合點參與函數模型的參數擬合(針對路線上數據)。

方案2：選取首都圈地區5條水準環內部路線全部點作為外部檢核點(共80個點)，其余639個點作為擬合點參與函數模型的參數擬合(針對環內部數據)。

方案3：均勻選取晉冀蒙地區125個點作為外部檢核點(約占總點數的1/5)，其余502個點作為擬合點參與函數模型的參數擬合(針對路線上數據)。

方案4：選取晉冀蒙地區5條水準環內部路線全部點作為外部檢核點(共60個點)，其余567個點作為擬合點參與函數模型的參數擬合(針對環內部數據)。

本文采用外符合精度及檢核點速率擬合值與實際觀測值之差(殘差)的絕對值大于2 mm/a的點的個數來衡量擬合的精度。外符合精度σ的表達式為

(16)

式中，Δi表示檢核點速率擬合值與實際觀測值之差；n為檢核點個數，并稱 Δi>2 mm/a的點為病態點。

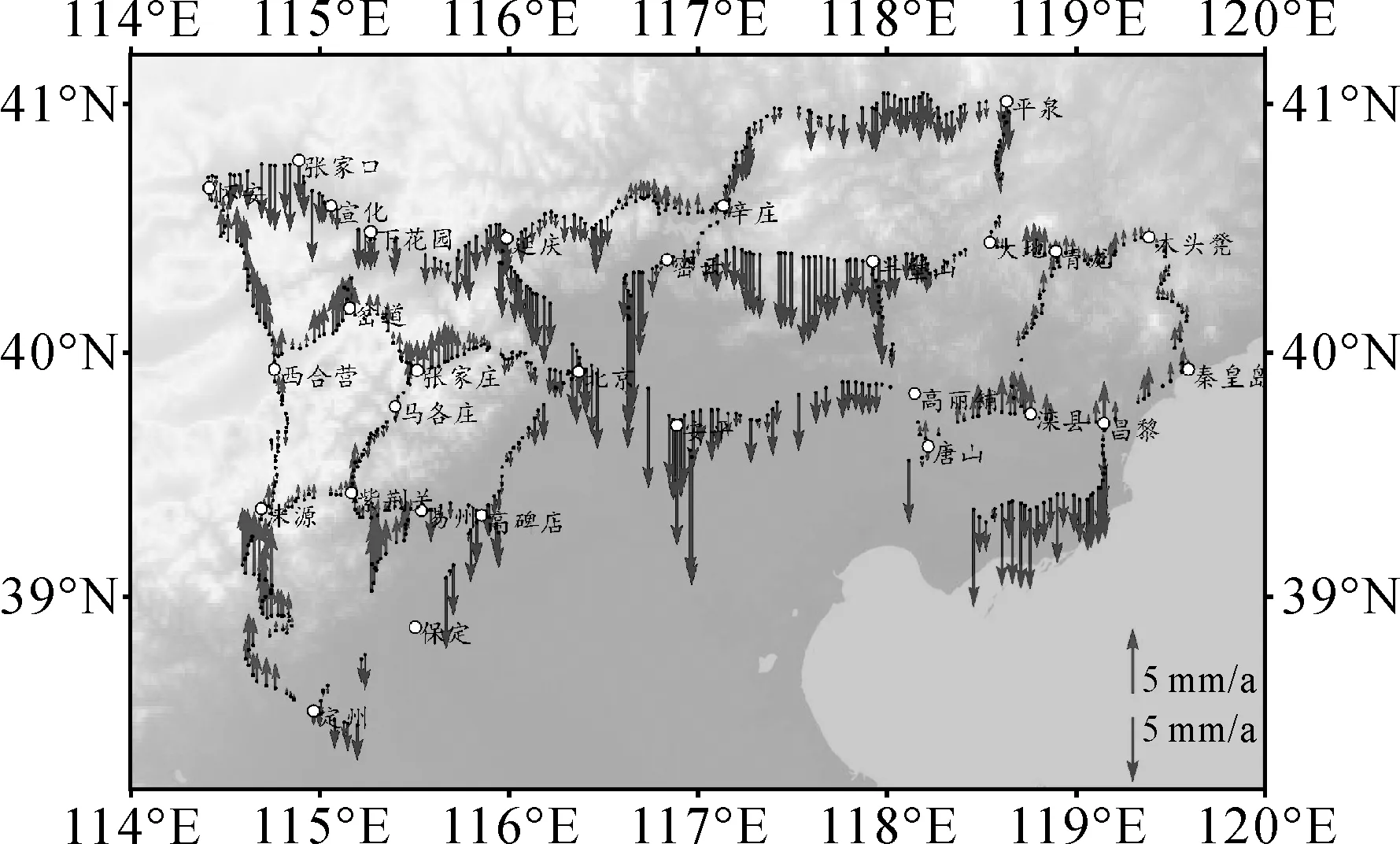
圖1 首都圈地區垂直形變速率(相對于北京)

圖2 晉冀蒙地區垂直形變速率(相對于大同)

2.2 各種模型擬合結果比較

對首都圈地區的擬合計算有方案1和方案2，各種模型擬合結果見表1。

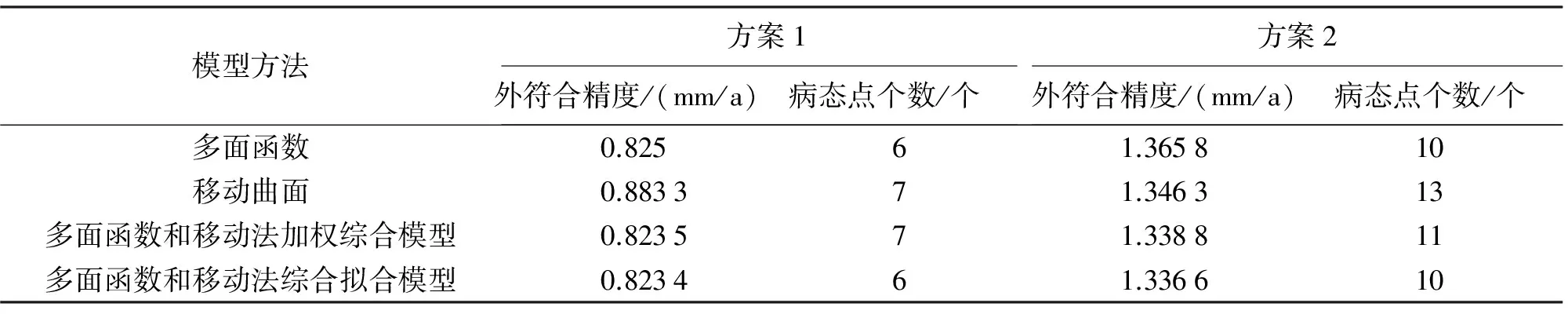
表1 首都圈地區各種模型擬合結果比較

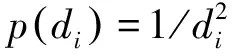
為了直觀地看出各種模型的擬合效果，給出不同模型在方案1和方案2中擬合檢核點速率殘差情況，如圖3和圖4所示。

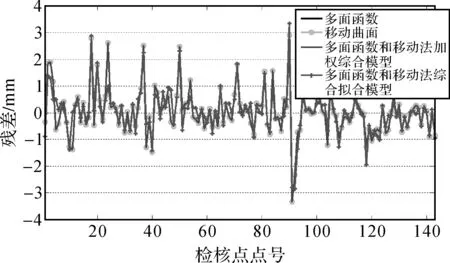
圖3 方案1不同模型檢核點擬合殘差

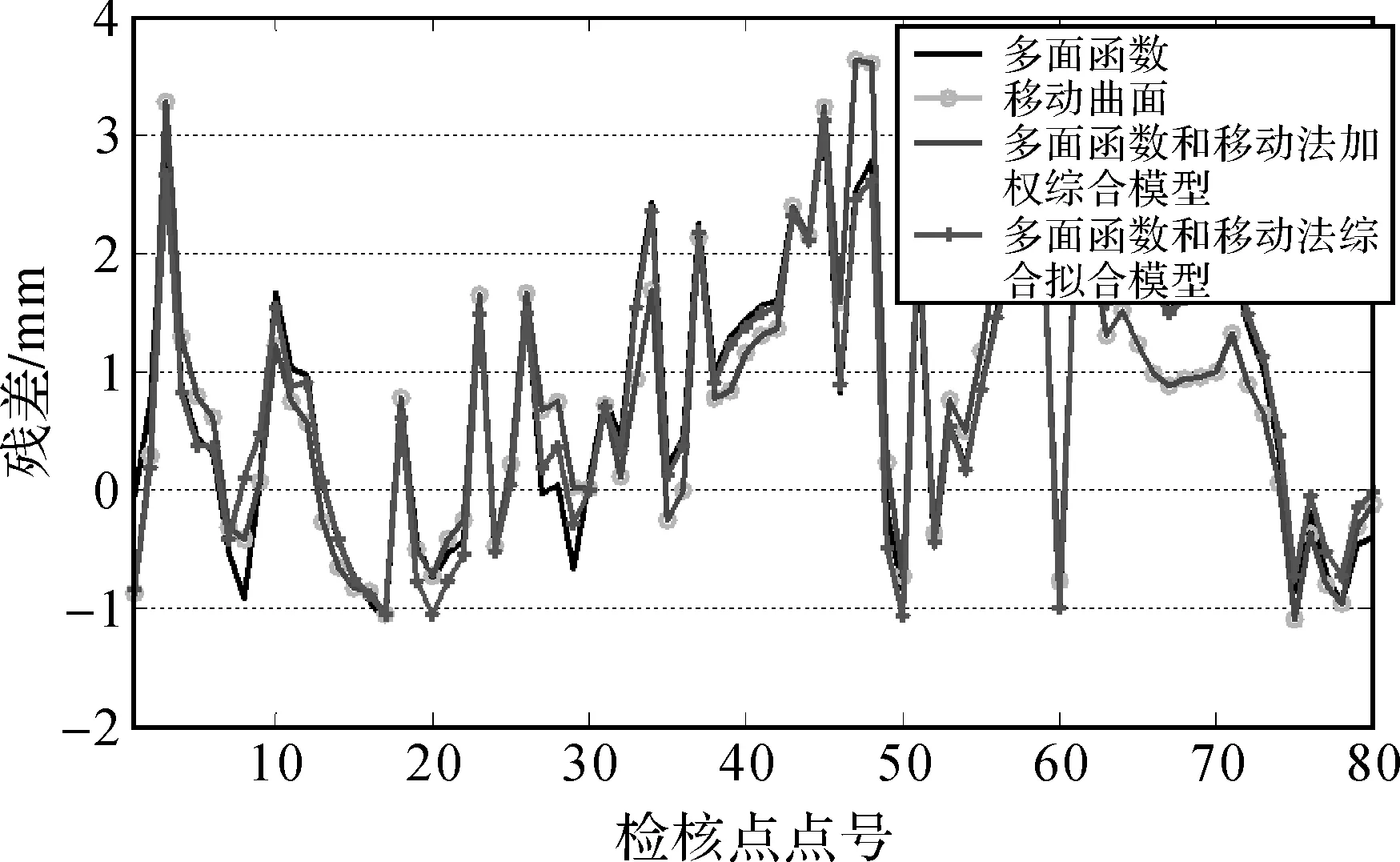
圖4 方案2不同模型檢核點擬合殘差

對晉冀蒙地區的擬合計算有方案3和方案4，各種模型擬合結果見表2。

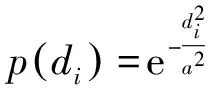
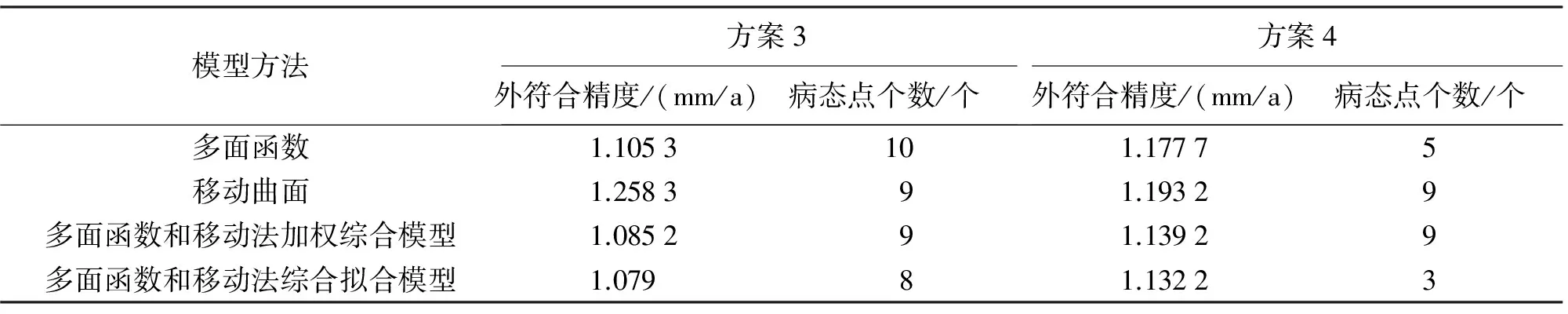
表2 晉冀蒙地區各種模型擬合結果比較

為了直觀地看出各種模型的擬合效果，給出不同模型在方案3和方案4中擬合檢核點速率殘差情況，如圖5和圖6所示。

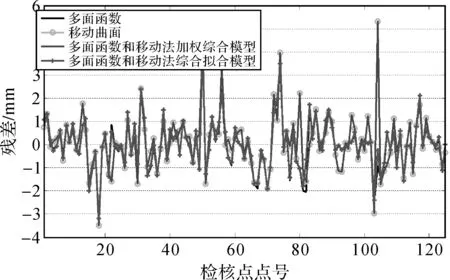
圖5 方案3不同模型檢核點擬合殘差

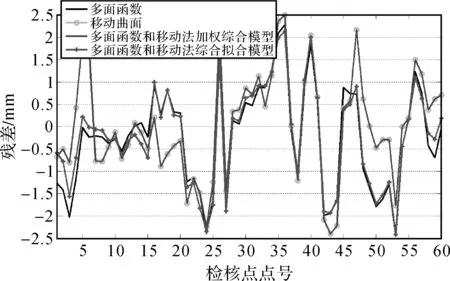
圖6 方案4不同模型檢核點擬合殘差

2.3 算例結果分析

(1) 從表1和表2中可以發現，4種模型中兩種綜合模型的擬合精度優于兩種單一模型，但是特性不同。多面函數和移動法加權綜合模型雖然精度上優于多面函數模型，但是病態點個數并不具有優勢，這是因為加權綜合會使得單一模型的各種誤差傳遞到最終結果中。而多面函數和移動法綜合擬合模型不管在精度上還是病態點個數上均優于多面函數模型。

(2) 多面函數和移動法綜合擬合模型在兩個地區4種不同情況下都是4種模型中擬合精度最高的，病態點數也是最少的，并且從圖4—圖7可以看出多面函數和移動法綜合擬合模型的擬合殘差是最穩定的。

2.4 等值線圖繪制

利用多面函數和移動法綜合擬合模型對首都圈和晉冀蒙地區的垂直形變速率進行擬合，并進行格網化處理，格網間距設為1′×1′，得到兩個地區的垂直形變速率等值線圖，如圖7和圖8所示。

從圖7和圖8可以發現首都圈和晉冀蒙兩個地區用多面函數和移動法綜合擬合模型得到的垂直形變速率等值線圖與圖1和圖2的速率圖反映的升降情況吻合度較好，說明該模型可以用于這兩個地區的垂直形變場擬合。

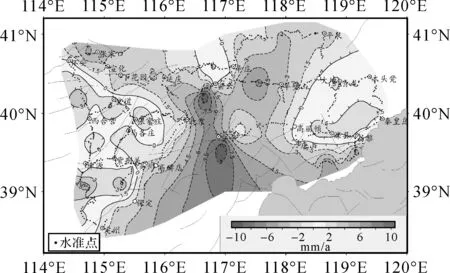
圖7 首都圈地區垂直形變速率等值線

圖8 晉冀蒙地區垂直形變速率等值線

3 結 論

(1) 兩種綜合模型的擬合精度優于兩種單一模型，但多面函數和移動法加權綜合模型會使得單一模型的各種誤差傳遞到最終結果中，從而導致病態點個數較多。而多面函數和移動法綜合擬合模型不管在精度上還是病態點個數上都優于多面函數模型。

(2) 多面函數和移動法綜合擬合模型在首都圈和晉冀蒙兩個地區4種情況下都是擬合精度最高、病態點數最少、擬合殘差最穩定的，并且應用該模型擬合這兩個地區的垂直形變場得到的等值線圖與速率圖吻合度較好，具有一定的實際應用價值。

[1] 郝明.基于精密水準數據的青藏高原東緣現今地殼垂直運動與典型地震同震及震后垂直形變研究[D].北京:中國地震局地質研究所，2012.

[2] 黃立人,楊國華,劉天奎.用速率面擬合法研究華北部分地區的現今地殼垂直運動[J].地殼形變與地震，1989,9(3):26-34.

[3] 趙承坤，黃立人.速率面擬合法中核函數中心點的選擇[J].地殼形變與地震，1991,11(2):48-54.

[4] 陶本藻,王新洲,于正林,等.用于垂直形變模型的多面函數擬合法的試驗研究[J].地殼形變與地震，1992，12(1)：1-12.

[5] 楊國華,黃立人.速率面擬合法中多面函數幾個特性的初步數值研究[J].地殼形變與地震，1990,10(4)：70-82.

[6] 黃立人,陶本藻,趙承坤.多面函數擬合在地殼垂直運動研究中的應用[J].測繪學報，1993,22(1):25-32.

[7] 劉經南,施闖,姚宜斌,等.多面函數擬合法及其在建立中國地殼平面運動速度場模型中的應用研究[J].武漢大學學報(信息科學版),2001，26(6):500-503.

[8] 王文利,陳士銀,董鴻聞,等.利用多面函數擬合中國陸地垂直運動速率圖[J].測繪通報,2002(8):6-8.

[9] 劉同文,楊志強,王慧敏.西秦嶺地區垂直形變的分析研究[J].測繪科學，2014，39(4)：61-63.

[10] 秦姍蘭,王慶良,季靈運,等.利用水準資料研究西秦嶺地區的垂直形變[J].大地測量與地球動力學，2012，32(2):16-19.

[11] 徐紹銓,張華海,楊志強,等.GPS測量原理及應用[M].武漢：武漢大學出版社，2008.

[12] 趙超英,張勤.地殼垂直形變場的綜合逼近模型[J].大地測量與地球動力學，2003，23(2)：42-44.

[13] 田曉，鄭洪艷，許明元,等.一種改進的適用于不同地形的GPS高程擬合模型[J].測繪通報，2017(1):35-38.