形態(tài)參數(shù)下地表采動裂縫三維建模及可視化方法
戴華陽,王 祥,李 軍,郭俊廷,閻躍觀
(1. 中國礦業(yè)大學(xué)(北京)地球科學(xué)與測繪工程學(xué)院,北京 100083; 2. 中國礦業(yè)大學(xué)(北京)煤炭資源與安全開采國家重點(diǎn)實(shí)驗(yàn)室,北京 100083)
煤炭開采在給人們帶來巨大經(jīng)濟(jì)效益的同時,也給環(huán)境帶來若干負(fù)面影響,其中突出的問題是開采引起的大量地表采動裂縫[1]。地表采動裂縫作為一種表生的地質(zhì)災(zāi)害現(xiàn)象,在世界許多國家普遍存在,并已成為一種主要的區(qū)域性地質(zhì)災(zāi)害現(xiàn)象,它對各類工程建筑、交通設(shè)施、城市生命線工程及土地資源造成了災(zāi)難性的直接破壞,并有可能引發(fā)嚴(yán)重的生態(tài)環(huán)境問題[2]。深入研究采動引起的地表裂縫并減緩和防治地裂縫災(zāi)害是資源安全開采和環(huán)境保護(hù)的重要內(nèi)容。當(dāng)前較為常用的地裂縫記錄和發(fā)布的方式是采用二維平面圖和剖面圖,但該方法會導(dǎo)致地表采動裂縫的大量空間信息丟失,同時加大理解和判別裂縫空間信息的難度[3]。因此,亟須研究一種合理、實(shí)用的地表采動裂縫三維建模及可視化方法,以實(shí)現(xiàn)對多類復(fù)雜采動裂縫結(jié)構(gòu)、形態(tài)、空間關(guān)系等的直觀認(rèn)知。
隨著近年來地理信息技術(shù)的不斷發(fā)展,三維建模及可視化技術(shù)已經(jīng)越來越受到青睞,地物地貌的三維模型不僅具有虛擬現(xiàn)實(shí)的真實(shí)感,而且能提供真實(shí)、準(zhǔn)確的三維地理坐標(biāo),便于進(jìn)行空間分析和空間運(yùn)算。目前三維建模的研究主要針對兩大類對象:人工構(gòu)筑物和自然地貌。人工構(gòu)筑物包括建筑、水塔、橋梁、管線等由人建造或構(gòu)建的物體,由于此類地物形狀相對規(guī)則,學(xué)術(shù)界和工業(yè)界已經(jīng)開發(fā)多種軟件,可以通過基本建模要素的組合實(shí)現(xiàn)。張暉等應(yīng)用CityEngine利用建筑物的基底投影數(shù)據(jù)及內(nèi)部房間分布矢量化數(shù)據(jù)生成建筑外立面三維模型[4];張帆等應(yīng)用Creator實(shí)現(xiàn)大范圍的虛擬城市三維建模[5];尹暉等利用Google SketchUp實(shí)現(xiàn)了對輸電桿塔、絕緣子及金具的建模[6]。與人工構(gòu)筑物不同,自然地貌或地質(zhì)體等的三維建模方法較多,主要分為3類:基于面表示的數(shù)據(jù)模型、基于體表示的數(shù)據(jù)模型和混合數(shù)據(jù)模型。不少學(xué)者在這方面開展了研究工作,如程朋根等研究了以似三棱柱體為體元的三維數(shù)據(jù)模型表達(dá)地質(zhì)體[7];顏輝武采用Kriging插值方法建立水文地質(zhì)層的三維模型,并利用體繪制技術(shù)進(jìn)行可視化表達(dá)[8]。雖然地理三維建模取得了很大進(jìn)展,但上述方法和軟件主要面向建筑物、管道、地質(zhì)體等地物地貌,若將其直接用于因礦物開采導(dǎo)致的地表裂縫的三維建模,會存在以下問題:①裂縫相對自然地表屬于微觀地貌特征,若要詳盡表達(dá)裂縫的幾何形態(tài)需采集大量的裂縫地貌特征點(diǎn),野外測繪工作量非常大;②依據(jù)開采沉陷規(guī)律,地表采動裂縫的形態(tài)具有典型的規(guī)律,而由高程測量點(diǎn)直接構(gòu)建TIN模型反映的裂縫形態(tài)和分布往往不能準(zhǔn)確展現(xiàn)其真實(shí)規(guī)律;③直接三維建模可視化結(jié)果通常難以獲得逼真的效果。為此,本文以空間插值和分形理論為基礎(chǔ),提出由裂縫的幾何形態(tài)預(yù)計(jì)參數(shù)對地表TIN模型進(jìn)行重構(gòu),以生成裂縫三維模型的方法,并利用ArcEngine平臺實(shí)現(xiàn)對裂縫的三維可視化。
1 方 法
1.1 地表采動裂縫三維建模總體流程
本文利用裂縫的形態(tài)預(yù)計(jì)參數(shù)信息構(gòu)建裂縫三維模型,該方法以采動前地表TIN模型為基礎(chǔ),根據(jù)裂縫分布及形態(tài)參數(shù)(寬度、深度、傾角、落差等)的預(yù)計(jì)結(jié)果,利用空間插值和分形算法重構(gòu)TIN模型,實(shí)現(xiàn)裂縫的三維可視化。具體方法流程如圖1所示。
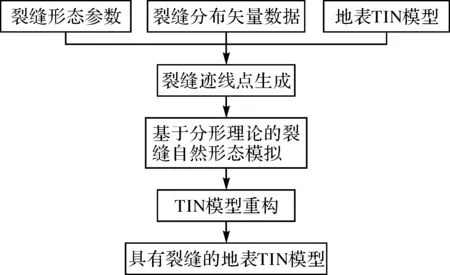
圖1 裂縫三維建模流程
1.2 模型輸入數(shù)據(jù)
地表裂縫三維建模涉及兩種輸入數(shù)據(jù):采動前地表的地形數(shù)據(jù)和裂縫的分布與形態(tài)參數(shù)。本文采用TIN模型表達(dá)采動前地形數(shù)據(jù),TIN模型將無重復(fù)的散亂數(shù)據(jù)點(diǎn)集按某種規(guī)則(如Delaunay規(guī)則)進(jìn)行三角剖分,使這些散亂點(diǎn)形成連續(xù)但不重疊的不規(guī)則三角面片網(wǎng),并以此來描述三維物體的表面[9]。TIN表面模型能以最少的控制點(diǎn)描述地表的空間形態(tài),適當(dāng)添加控制點(diǎn)可在不同程度上改善細(xì)節(jié)信息,使其更接近真實(shí)的自然狀態(tài)[10],而減少部分控制點(diǎn)能降低局部工作量而不影響目標(biāo)的空間形態(tài)表達(dá)。特別對于含有大量特征(如地性線、斷裂線、構(gòu)造線)的地形,TIN模型能很好地展示這些特征,更精確、高效、合理地表達(dá)地表形態(tài)[11]。
地表采動裂縫的剖面通常呈“V”字形[12],平面呈帶狀分布,但由于采動過程差異,地表形成的裂縫會呈現(xiàn)不同的幾何形態(tài),常見的裂縫形態(tài)包括:直線型裂縫、鋸齒型裂縫、復(fù)雜曲線裂縫、分叉型裂縫、臺階狀裂縫等。對于不同形態(tài)的裂縫,其形態(tài)參數(shù)表達(dá)方式也會有所差異,見表1。

表1 裂縫類型及形態(tài)參數(shù)
建模時,首先導(dǎo)入采動前地表TIN模型和描繪裂縫空間分布的坐標(biāo)串(以矢量線要素表達(dá)),并輸入裂縫幾何形態(tài)參數(shù),具體定義如下:
裂縫寬度:采動裂縫在地表上呈現(xiàn)的寬度,一般在幾厘米到幾十厘米之間,較寬裂縫可達(dá)1 m以上。
裂縫深度:采動裂縫從地表到地下最低點(diǎn)的延伸距離。
裂縫傾角:采動裂縫坡面與水平面的夾角。
1.3 裂縫跡線點(diǎn)生成
本文使用一系列有序離散點(diǎn)描述地表采動裂縫在平面的幾何形態(tài),并將這些離散點(diǎn)定義為裂縫的跡線點(diǎn),包括中線跡線點(diǎn)和邊界跡線點(diǎn)。在建模過程中,通過對輸入的裂縫矢量線要素的節(jié)點(diǎn)進(jìn)行加密生成中線跡線點(diǎn),然后以中線跡線點(diǎn)為基礎(chǔ),依據(jù)裂縫的幾何形態(tài)參數(shù)推求邊界跡線點(diǎn)。由于裂縫是在三維空間中建模,因此需同時計(jì)算跡線點(diǎn)的平面坐標(biāo)與高程,計(jì)算方法如下:
1.3.1 跡線點(diǎn)的平面坐標(biāo)計(jì)算
邊界跡線點(diǎn)的平面位置按緩沖區(qū)生成方法計(jì)算,涉及的幾何關(guān)系如圖2所示。
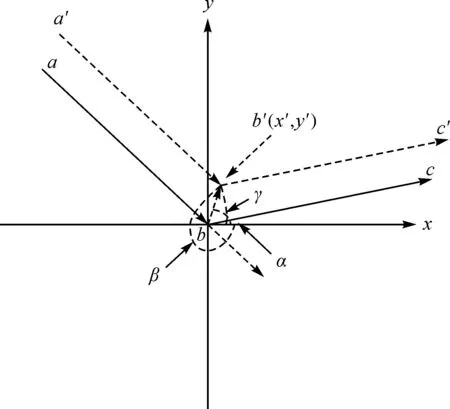
圖2 跡線點(diǎn)平面坐標(biāo)計(jì)算

α=arctanxc-xb,yc-yb
(1)
β=arctanxb-xa,yb-ya
(2)
κ=β-α-π/2
(3)
γ=α+κ
(4)
d=t/sinκ
(5)
(6)
式中,t為距離參數(shù),可為正負(fù)不同的值。t為正時,b′位于中心折線右側(cè);t為負(fù)時,b′位于中心折線左側(cè)。
1.3.2 跡線點(diǎn)的高程計(jì)算
跡線點(diǎn)高程根據(jù)地形數(shù)據(jù)和跡線點(diǎn)的平面位置計(jì)算。首先對跡線點(diǎn)進(jìn)行定位,即確定跡線點(diǎn)位于哪個TIN三角形內(nèi)(或邊線上),然后根據(jù)此三角形頂點(diǎn)的高程值利用趨勢面分析法計(jì)算跡線點(diǎn)高程。
根據(jù)三角形頂點(diǎn)坐標(biāo)和矢量拓?fù)潢P(guān)系判定跡線點(diǎn)位置的方程為
Li=ai+bix+ciyi=1,2,3
(7)
式中,ai、bi、ci是由三角形頂點(diǎn)pi的坐標(biāo)xi,yi確定的3個常數(shù),分別可由下面公式求得
(8)
跡線點(diǎn)的定位過程如圖3所示。設(shè)三角形p1p2p3為搜索的起點(diǎn),計(jì)算點(diǎn)p的面積坐標(biāo)得L<0,取L1的對應(yīng)邊p2p3的鄰接三角形p3p2p4作為下一個判斷的三角形。依次進(jìn)行判斷,直至三角形p7p6p8。此時若L1、L2、L3都大于0,則點(diǎn)p在三角形p7p6p8內(nèi);若Lii=1,2,3=0,則點(diǎn)p在Li所對應(yīng)的邊上。

圖3 跡線點(diǎn)在三角網(wǎng)中的定位過程
若點(diǎn)p位于某三角形內(nèi)部或其中一條邊上,利用趨勢面分析法計(jì)算跡線點(diǎn)高程值
zx,y=b0+b1x+b2y
(9)
根據(jù)式(9)建立法方程
(10)
改寫成矩陣形式為
(11)
通過矩陣求逆得
(12)
將b0、b1、b2代入式(7)中,求出跡線點(diǎn)p的高程。若是邊界跡線點(diǎn),則跡線點(diǎn)高程即為求得的高程值;若是中線跡線點(diǎn),需要在所求高程值基礎(chǔ)上減去裂縫深度。
在建模過程中需要注意,過多的跡線點(diǎn)會增加建模的時間成本。因此,建模時應(yīng)在最大限度地保留裂縫幾何形態(tài)特征的前提下,盡量減少跡線點(diǎn)的數(shù)量,提高建模效率。
1.4 基于分形理論的裂縫自然形態(tài)模擬
圖4為根據(jù)所生成的跡線點(diǎn)呈現(xiàn)出的地表裂縫形態(tài),可以看出這樣的幾何形態(tài)過于規(guī)則化,不能逼真反映地表采動裂縫在自然界中的真實(shí)形態(tài)。

圖4 由原始跡線點(diǎn)構(gòu)成的裂縫幾何形態(tài)
為模擬地表采動裂縫的真實(shí)形態(tài),本文基于分形理論[13-16]使用改進(jìn)后的中點(diǎn)細(xì)分內(nèi)插方法[17-18],從分?jǐn)?shù)維度視角利用較少的基元和跡線參數(shù)推演裂縫邊界。內(nèi)插方法如圖5所示。
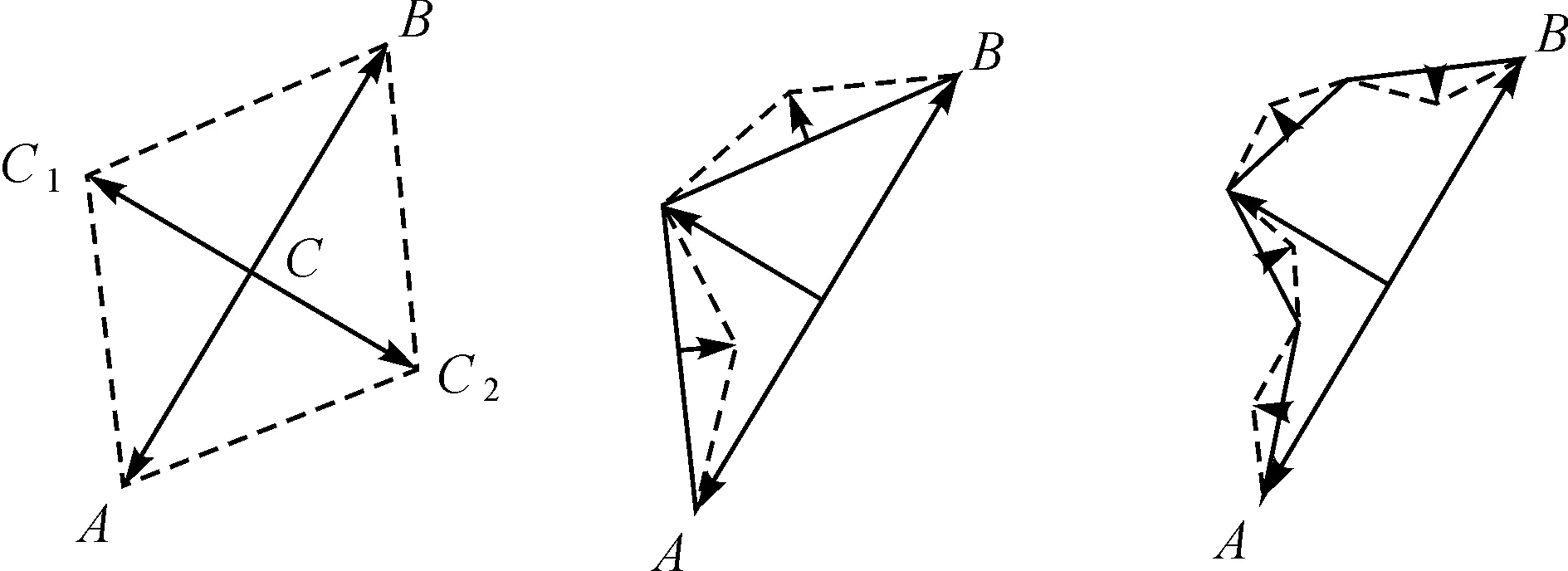
圖5 中點(diǎn)細(xì)分內(nèi)插方法
基元AB為相鄰邊界跡線點(diǎn)A和跡線點(diǎn)B連接而成的線段,在基元線段AB中點(diǎn)C處沿AB中垂線方向隨機(jī)地移動一段距離L,得到位移后的新點(diǎn)C1(或C2),將跡線點(diǎn)A、B及新點(diǎn)C1(或C2)順序相連,得到分形元AC1B。新點(diǎn)的偏移方向由一隨機(jī)方向參數(shù)J跡線。當(dāng)J>0時,新點(diǎn)在AB右側(cè)生成;當(dāng)J≤0時,新點(diǎn)在AB左側(cè)生成。將生成的分形元作為新的基元利用相同的方法進(jìn)行迭代,不斷推求出更小的分形元,直到滿足給定的迭代次數(shù)。新點(diǎn)的坐標(biāo)方程為
X=XA+XB/2+ΔX
(13)
Y=YA+YB/2+ΔY
(14)
式中,XA、YA分別為跡線點(diǎn)A在X軸和Y軸的坐標(biāo)分量;XB、YB分別為跡線點(diǎn)B在X軸和Y軸的坐標(biāo)分量。ΔX、ΔY為與AB長度有關(guān)的隨機(jī)坐標(biāo)偏移量,可根據(jù)跡線點(diǎn)的走向和點(diǎn)C的偏向求算。在保證不會造成地裂縫中斷的前提下,X、Y加上隨機(jī)坐標(biāo)偏移量后可以使新跡線點(diǎn)C1(或C2)更具不定因素,能模擬裂縫的不規(guī)則特征[19-20]。圖6展示了加入分形特征后裂縫的自然幾何形態(tài)。

圖6 具有分形特征的裂縫自然幾何形態(tài)
1.5 TIN模型重構(gòu)
經(jīng)過上述步驟生成了具有分形特征的裂縫跡線點(diǎn),對裂縫進(jìn)行三維建模,即將這些跡線點(diǎn)融入采動前地表的TIN模型中。為確保在重構(gòu)后TIN模型中表達(dá)出裂縫形態(tài),并避免非裂縫區(qū)域發(fā)生變形,本研究將裂縫邊界設(shè)置為隔斷線,可以約束TIN的三角網(wǎng)重構(gòu)僅在非裂縫區(qū)域進(jìn)行,且使裂縫邊界上的節(jié)點(diǎn)也參與重構(gòu)。在裂縫區(qū)域內(nèi),移除TIN模型的原始節(jié)點(diǎn),最終得到可以反映裂縫分布及三維空間形態(tài)的TIN模型。
需要注意的是,一旦三角網(wǎng)被修改,必須進(jìn)行LOP優(yōu)化。使用Delaunay空外接圓準(zhǔn)則檢查新生成三角形,如不滿足,則調(diào)換與相鄰三角形所組成的凸四邊形的對角線。若對角線發(fā)生交換,則繼續(xù)向相鄰三角形擴(kuò)展此過程,直至滿足空外接圓準(zhǔn)則或到達(dá)三角網(wǎng)邊界。
2 原型系統(tǒng)開發(fā)與應(yīng)用實(shí)例
2.1 開發(fā)環(huán)境
基于上述方法,本文以Visual Studio 2010作為開發(fā)工具,選擇C#為開發(fā)語言,利用ArcEngine三維分析類庫及相關(guān)算法,開發(fā)了對多類型復(fù)雜地表采動裂縫進(jìn)行建模與可視化的原型系統(tǒng)。該系統(tǒng)能根據(jù)采動前地表TIN模型和裂縫形態(tài)參數(shù)快速生成三維裂縫模型,還支持從不同角度、方位和距離展示裂縫,并可以通過裂縫所在地質(zhì)體的任意旋轉(zhuǎn)、移動、漫游、視景變換等操作對地裂縫進(jìn)行詳察。
2.2 應(yīng)用實(shí)例
本文以東峽礦區(qū)為試驗(yàn)區(qū),對該區(qū)域內(nèi)因采煤導(dǎo)致的地表裂縫進(jìn)行建模。東峽煤礦位于中國甘肅省華亭縣境內(nèi),地理坐標(biāo)為東經(jīng)106°40′14″,北緯35°12′04″,西距華亭縣城1.8 km。礦區(qū)井田內(nèi)地形復(fù)雜,溝壑縱橫,沖溝發(fā)育,表層幾乎全為黃土層所覆蓋,主要形成大小不等的梁卯相間的黃土低山丘陵地貌景觀。最高海拔為1 701.3 m,最低海拔為1 525.1 m,總體地勢東南高,西北低。
近10年來,隨著煤炭工業(yè)的迅速發(fā)展,東峽礦區(qū)內(nèi)先后建設(shè)了一批地方煤礦、鄉(xiāng)鎮(zhèn)煤礦及國有大中型礦井,煤炭工業(yè)成為當(dāng)?shù)氐闹еa(chǎn)業(yè)之一。但隨著開采量的不斷增加,采動過程中地表塌陷愈發(fā)嚴(yán)重,并出現(xiàn)了各種不同形態(tài)的采動裂縫。本文選取了該區(qū)域內(nèi)若干具有典型特點(diǎn)的裂縫,從多個視角展示裂縫三維建模效果。圖7展示了裂縫在Google Earth高分辨率影像中的效果和利用本文方法建模的可視化效果。
裂縫群中心位置位于北緯35°12′49.34″、東經(jīng)106°39′54.00″,裂縫長度從20 m到200 m不等,裂縫類型以曲線型為主。區(qū)域1的裂縫為俯視角度,可以看出建模結(jié)果準(zhǔn)確反映了裂縫的真實(shí)位置分布。區(qū)域2和區(qū)域3為側(cè)視角度,體現(xiàn)出本文方法很好地展示了山體不同高度處的裂縫狀態(tài)。區(qū)域4為裂縫的近距離展示,可以看出帶有分形特征的模型逼真地展現(xiàn)了裂縫的不規(guī)則自然形態(tài)。
為更好地展示生成裂縫后的TIN模型,著重展示研究區(qū)中的單條裂縫的效果,如圖8所示,左側(cè)為裂縫的渲染圖,右側(cè)為對應(yīng)裂縫的TIN模型,包括節(jié)點(diǎn)的分布和連接狀態(tài)。
2.3 復(fù)雜裂縫模擬
為更好地展示本文方法及原型系統(tǒng)在模擬更復(fù)雜裂縫形態(tài)的效果,通過人工設(shè)置裂縫形態(tài)參數(shù),模擬出臺階型裂縫、復(fù)雜曲線裂縫、弧線型裂縫和交叉型裂縫,分別如圖9—圖12所示。由圖可看出,本文方法能模擬出任意復(fù)雜形態(tài)的裂縫并能清晰地反映細(xì)節(jié)信息,無論是對裂縫可視化還是定量空間分析都具有非常好的效果。
3 結(jié) 語
地表采動裂縫是伴隨著地下煤炭等資源開采的一種表生地質(zhì)災(zāi)害現(xiàn)象,對裂縫的三維建模與可視化研究將促進(jìn)裂縫的形狀、成因研究,并為開采沉陷監(jiān)測和生態(tài)環(huán)境恢復(fù)提供科學(xué)支持,具有重要的實(shí)際應(yīng)用價值。本文結(jié)合三維地形建模、分形、空間插值等理論,提出了基于幾何形態(tài)參數(shù)的地表裂縫三維建模方法,并利用ArcEngine平臺編程實(shí)現(xiàn)了裂縫的三維建模與可視化功能。

圖7 東峽礦區(qū)地表裂縫建模效果對比
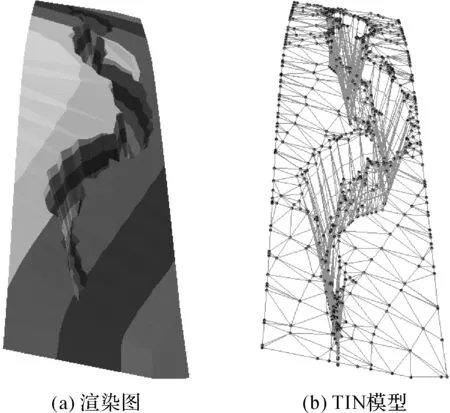
圖8 裂縫的TIN模型

圖9 臺階型裂縫

圖10 復(fù)雜曲線裂縫

圖11 弧線型裂縫
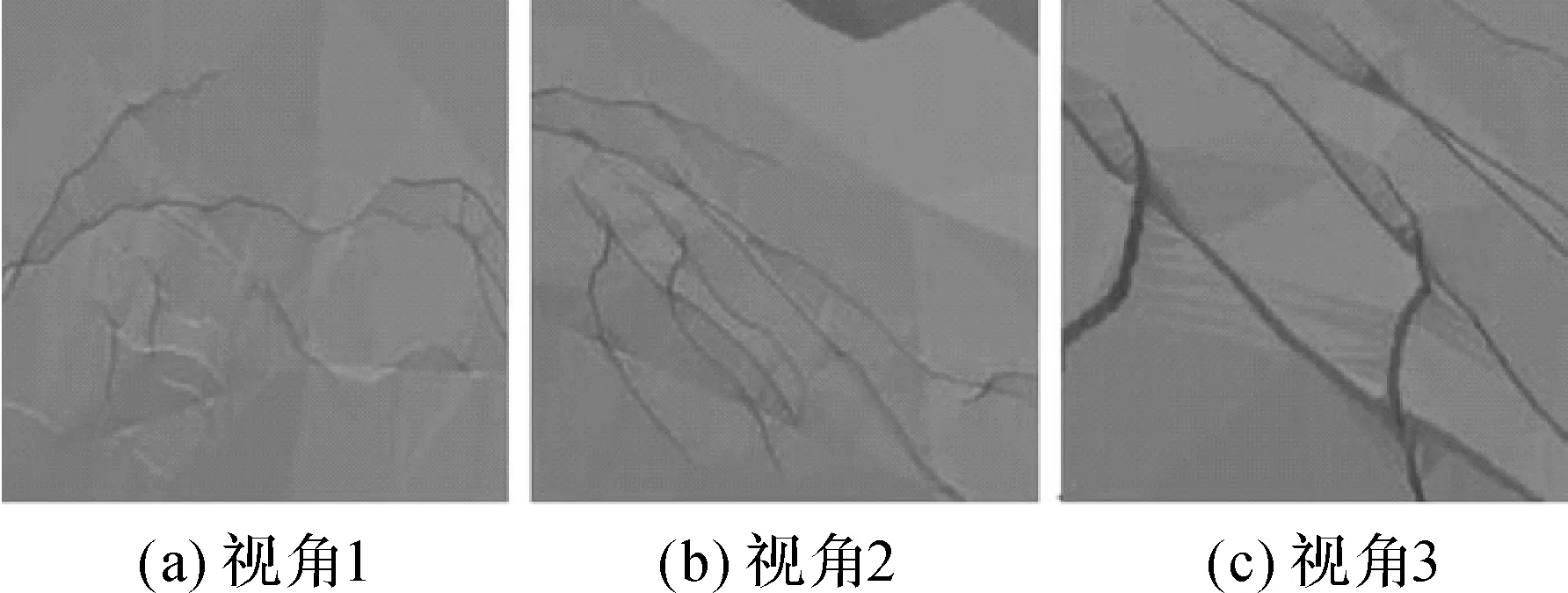
圖12 交叉型裂縫
本文選擇了東峽礦區(qū)為試驗(yàn)區(qū),利用提出的方法對典型區(qū)域的地表裂縫進(jìn)行三維模擬,能真實(shí)逼真呈現(xiàn)裂縫的形態(tài)、延伸與細(xì)節(jié)信息。通過與實(shí)測數(shù)據(jù)對比,驗(yàn)證了該方法的有效性和準(zhǔn)確性。但本文提出的建模方法、思路,僅僅是對地表采動裂縫在三維環(huán)境下分析與模擬的開始,仍然有許多問題需要繼續(xù)探索,包括數(shù)據(jù)的多元化、高效存儲方式、三維空間分析及應(yīng)用等方面。
[1] 謝和平,王金華,申寶宏,等.煤炭開采新理念——科學(xué)開采與科學(xué)產(chǎn)能[J].煤炭學(xué)報,2012,37(7):1069-1079.
[2] 胡青峰,崔希民,袁德寶,等.厚煤層開采地表裂縫形成機(jī)理與危害性分析[J].采礦與安全工程學(xué)報,2012,29(6):864-869.
[3] 張立強(qiáng),譚玉敏,康志忠,等.一種地質(zhì)體三維建模與可視化的方法研究[J].中國科學(xué)(D輯:地球科學(xué)),2009(11):1625-1632.
[4] 張暉,劉超,李妍,等.基于CityEngine的建筑物三維建模技術(shù)研究[J].測繪通報,2014(11):108-112.
[5] 張帆,史瓊芳,達(dá)漢橋.Creator應(yīng)用于虛擬城市三維建模的關(guān)鍵技術(shù)與實(shí)踐[J].測繪工程,2005,14(4):55-57.
[6] 尹暉,孫夢婷,干喆淵,等.基于SketchUp的輸電桿塔三維建模研究[J].測繪通報,2015(4):34-37.
[7] 程朋根,龔健雅,史文中,等.基于似三棱柱體的地質(zhì)體三維建模與應(yīng)用研究[J].武漢大學(xué)學(xué)報(信息科學(xué)版),2004,29(7):602-607.
[8] 顏輝武,祝國瑞,徐智勇,等.基于Kriging水文地質(zhì)層的三維建模與體視化[J].武漢大學(xué)學(xué)報(信息科學(xué)版),2004,29(7):611-614.
[9] 劉永和,張萬昌.不規(guī)則三角網(wǎng)的幾種數(shù)據(jù)結(jié)構(gòu)及其存儲機(jī)制研究[J].測繪科學(xué),2010,35(3):115-117,65.
[10] 羅勝,姜挺,江剛武,等.基于原始LiDAR點(diǎn)云TIN模型的建筑物自動提取[J].測繪通報,2012(S1):334-337.
[11] 熊祖強(qiáng),賀懷建,夏艷華.基于TIN的三維地層建模及可視化技術(shù)研究[J].巖土力學(xué),2007,28(9):1954-1958.
[12] 劉一冬,朱琳,于軍,等.一種地裂縫地質(zhì)體三維模型建模方法[J].地理與地理信息科學(xué),2016,32(2):51-54,66.
[13] 李宏艷,王維華,齊慶新,等.基于分形理論的采動裂隙時空演化規(guī)律研究[J].煤炭學(xué)報,2014,39(6):1023-1030.
[14] 呂秀琴,張毅.分形模擬在DEM內(nèi)插中的應(yīng)用[J].測繪科學(xué),2012,37(2):107-109.
[15] ZHU Xiaohua.Fractal Character of China Bedrock Coastline[J].Chinese Journal of Oceanology and Limnology,2004,22(2):130-135.
[16] LIU Chengyu,CHAO Jinlong,GU Wei,et al.On the Surface Roughness Characteristics of the Land Fast Sea-ice in the Bohai Sea[J].Acta Oceanologica Sinica,2014,33(7):97-106.
[17] 梁俊,王琪,劉坤良,等.基于隨機(jī)中點(diǎn)位移法的三維地形模擬[J].計(jì)算機(jī)仿真,2005,22(1):213-215.
[18] 梁俊,蔣金龍,趙雪蓮,等.隨機(jī)中點(diǎn)位移法在三維地形插值顯示的適用性分析[J].測繪科學(xué),2007,32(3):44-46,193.
[19] 陸娟,王建,朱曉華,等.海岸線分形模擬方法及其應(yīng)用——以江蘇省為例[J].黃渤海海洋,2002,20(2):47-52.
[20] 陸娟,王建,石麗.基于GIS和分形理論的海岸線模擬方法研究[J].中國圖象圖形學(xué)報,2003,8(6):692-696.

