圓錐曲線經典問題透析
■山東省壽光現代中學 陳傳璐
高考中圓錐曲線經典問題主要是圍繞“圓錐曲線的離心率、焦點弦長公式的應用、軌跡方程的探究、直線與圓錐曲線的位置關系、定值、定點、最值、范圍及探索性”等展開的,本文透析如下。
透析1——探究a,c滿足的關系求離心率的值或范圍
例1 (2 0 1 7年新課標Ⅱ卷原創押題預測卷0 1)如圖1,雙曲線的中心在坐標原點,焦點在x軸上,A1,A2為雙曲線實軸的頂點,B1,B2為雙曲線虛軸的端點,F2為右焦點,延長B1A2與F2B2交于點P,若∠B1P B2為銳角,則該雙曲線的離心率的取值范圍是( )。
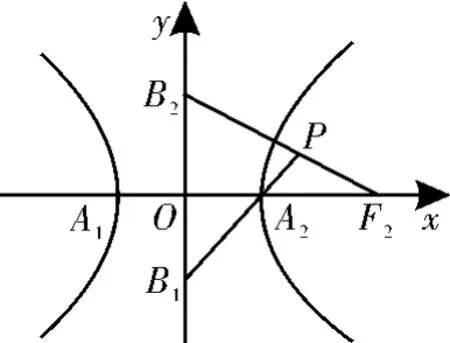
圖1

解析:利用向量的夾角為銳角構建a,c的二次不等式,再求解范圍。設B1(0,-b),B2(0,b),F2(c,0),A2(a,0),所以因為∠B1P B2為銳角,所以的夾角為銳角,所以,即a2-c2+a c>0。兩邊同時除以a2并化簡得e2-e-1<
感悟:橢圓和雙曲線的離心率的求值及范圍,關鍵就是確立一個關于a,b,c的方程或不等式,再根據a,b,c的關系消掉b得到a,c的關系式,進而構建關于a,c的齊次式方程或不等式,要充分利用橢圓和雙曲線的幾何性質、點的坐標的范圍和題設的關系等。
透析2——拋物線焦點弦長有關結論的探究及應用
例2 (2 0 1 7年第二次全國大聯考新課標Ⅰ卷)已知拋物線y2=2p x(p>0)的焦點為F,拋物線上一點P的橫坐標為2,Q(x,y),P(x0,y0)。過F且傾斜角為3 0°的直線交拋物線于A,B兩點,O為坐標原點,則△O A B的面積為____。
解析2:用方程可探究拋物線焦點弦長的有關結論,注意簡化運算途徑的選擇。
感悟:本題解析2的探究過程可得到拋物線焦點弦的幾個常用結論:
(1)弦端點A(x1,y1),B(x2,y2)的坐標之間的關系為
(3)弦被焦點分弦所成的兩焦半徑的倒數和為p的倒數的2倍,即
透析3——定點和定值問題的探究
上,橢圓C的左焦點為(-1,0)。
(1)求橢圓C的方程。
(2)如圖2,直線l過點T(m,0)(m>0)交橢圓C于M,N兩點,A B是橢圓C經過原點O的弦,且MN∥A B,問:是否存在正數m,使得為定值?若存在,請求出m的值;若不存在,請說明理由。
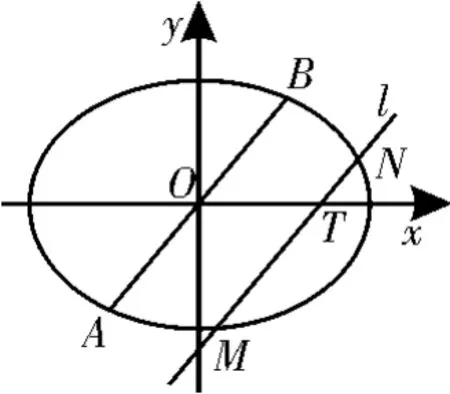
圖2
解析:(1)由左焦點(-1,0)可得c=1,因為b2=a2-c2,所以b2=a2-1。
(2)假設正數m存在,設直線l:y=k(x-m),M(x1,y1),N(x2,y2),聯立方程消去y整理得(3+4k2)x2
設A(x3,y3),B(x4,y4),聯立方程組消去y整理得
透析4——圓錐曲線中的最值或范圍問題
例4 (2 0 1 7年新課標Ⅰ卷原創押題預測卷0 1)已知橢圓的左右焦點分別為F1,F2,上下頂點分別是B1,B2,C是B1F2的中點,若且C F1⊥B1F2。
(1)求橢圓C的標準方程;
(2)過F2的直線l與橢圓C交于不同的兩點A,D,求△F1A D的面積的最大值。
解析:(1)由題意可得F1(-c,0),F2(c,,所以
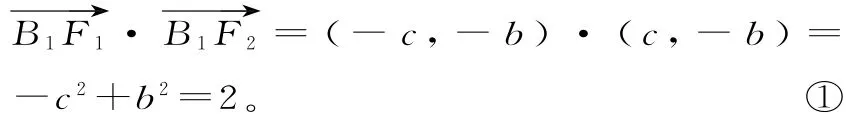
由C F1⊥B1F2,可得,即
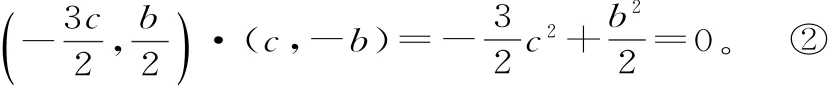
(2)設 A(x1,y1),D(x2,y2),S△F1AD=。由題意知,直線l的斜率不為零,可設直線l的方程消去x整理得為x=m y+1,由(3m2+4)y2+6m y-9=0,所以y1+
因為直線l與橢圓C交于不同的兩點,所以Δ>0,即(6m)2+3 6(3m2+4)>0,m∈R, 故 S△F1AD=|y1-y2|=。令t=,則t≥1,則。令,由函數的性質可知,函數f(t)在上是單調遞增函數,即當t≥1時,f(t)在[1,+∞)上單調遞增,因此有f(t)≥f(1)=,所以S△F1AD≤3,所以當t=1,即m=0時,S△F1AD最大,最大值為3。
感悟:解決圓錐曲線中的最值或范圍問題有兩種途徑:一是用圓錐曲線的定義和平面幾何的有關結論來解決;二是將圓錐曲線中的最值或范圍問題轉化為函數問題,然后根據函數的特征選用參數法、配方法、判別式法、三角函數有界法、函數單調性法及均值不等式法求解,其中換元法在化繁為簡時需認清函數的特征。

