碎紙片自動拼接復原

廖敏瑜，謝睿誠，余聲宇

（汕頭大學理學院數學系，廣東 汕頭 515063）

0 引言

破碎文件的拼接在司法物證復原、歷史文獻修復以及軍事情報獲取等領域都有著重要的應用.傳統上，拼接復原工作過分依賴人為干涉，當碎片數量巨大，內容復雜時，不但耗費大量的時間及人力，還可能對紙張信息造成損害.若紙張信息隱秘，還可能人為泄密造成不可估量的危害.因此，全自動拼接碎紙片的技術是十分必要的.

文獻[1]和文獻[2]研究了通過碎中文紙片內的文字行特征和表格特征來進行拼接，這種方法提高了拼接效率和降低了拼接難度，但是仍需要較多的人工干預進行拼接.文獻[3]研究的算法正確率高，但是僅適用于中文碎紙片的拼接不適用于英文碎紙片的拼接.文獻[4]是研究英文碎紙片的拼接，但是其摻雜了較多人工干預，而且各操作之間的連帶作用強，即前面操作錯誤就會導致后面的錯誤.文獻[5]通過聚類將碎紙片進行行分類，能夠不受人工干預就實現碎紙片的拼接，這種方法能夠將字母行位置相差明顯的碎紙片進行聚類，但是卻不能將字母行位置相差較小乃至無差距的碎紙片進行聚類，因此不能普遍解決碎紙片拼接問題.文獻[6]研究雙面英文碎紙片的拼接，提出一種運用聚類分析、MATLAB搜索算法和人工干預等相結合的方法，但其加入太多的人為干預.

為了得到無人工干預且適用性廣的碎紙片拼接方案，本文提出一種基于改進的遺傳算法（GA）及光學字符識別技術（OCR）的自動化拼接算法.針對英文文檔，通過研究碎紙片英文字母所在行的幾何特征信息及消除同行字母高度不同的干擾，對碎紙片進行分類；該分類是通過英文字母所在標準四格線的中部下基線的位置來構建的.將分類后的碎紙片間的拼接問題轉化為旅行商問題，采用改進的GA算法和OCR技術處理問題.通過字母中部下基線的位置及以貪婪算法為輔，處理組行成頁的問題.最后，本文還將對英文碎紙片拼接的方案推廣，結合中文文字的特點，將算法改裝為能夠處理中文碎紙片拼接問題.

本文采用2013年全國大學生數學建模競賽B題[8]209個英文碎紙片和209個中文碎紙片圖像（分別由一個A4大小的英文文檔碎紙片經橫縱切成11×19，大小都為row×col的規則碎紙片）作為仿真數據.

1 英文碎紙片拼接原理

1.1 文檔分類

通過觀察，英文字母與中文漢字具有不同的結構特征.在中文文檔中，同行文字的高度基本一致，而英文文檔中，同行英文字母高度一般不統一.將印刷字母放置于四線格上，可將其分為四線格的上、中、下3部（記為上部，中部，下部）由印刷字母的特點及英文文章中各字母出現的頻率統計結果可知，所有大寫字母都占上中部，有9個小寫字母（b，d，f，h，i，j，k，l，t）是有占上部，占比約為 28.95%，有 5 個小寫字母（g，j，p，q，y）是有占下部，占比約為6.17%，所有的小寫字母都有占中部.由上面的分析可知，英文字母中部能有效提供行分類的信息，而上下部則會對行分類產生干擾，且下部對行分類的干擾較少.為此，記英文字母中部和下部之間的分界線為下基線，如圖1所示.

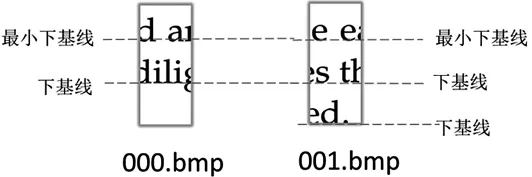
圖1 英文基線位置

如果碎紙片處于同一行中，則它們的部分下基線的位置基本相同.本文將最小下基線位置基本相同的碎紙片歸為一類，得到的類別有兩種情形：

（1）單行混合：當一行碎紙片的最小下基線與其他行的區別較大時，可將這一行碎紙片可歸為一類，得到單行混合的情況.

（2）多行混合：當一行碎紙片的最小下基線與其他部分行的區別較小乃至沒有區別時，可將其歸為一類，得到多行混合的情況.

1.2 行首和行尾的確定

分類后，每一類碎紙片中行首和行尾碎紙片個數與其組合行數一樣.由于文檔存在頁邊距，如圖2所示，所以本文通過處于行首碎紙片的左端和處于行尾碎紙片的右端存在較多空白，分別確定處于行首和行尾的碎紙片.

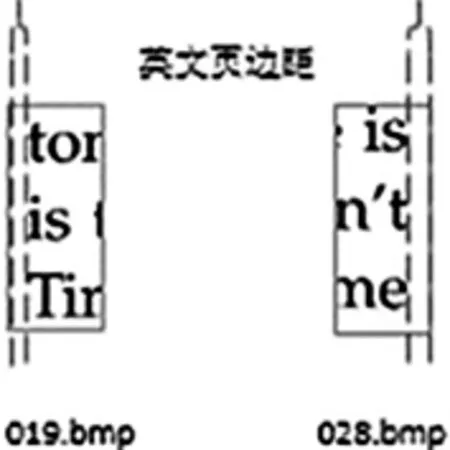
圖2 邊界位置

1.3 行內拼接

由于各碎紙片的縱向長度較小，如果依次匹配邊界不匹配距離最小的碎紙片，會造成很大的偏差.根據文獻[3]，本文類比旅行商問題設計問題：將各個碎紙片作為訪問點，定義碎紙片之間的距離，從行首碎紙片出發，經過其它碎紙片各一次，最后回到行尾碎紙片.將行內碎紙片的最佳排列問題轉化為相應的旅行商問題的最優解.

針對1.1的情形（1）中碎紙片的拼接：由于訪問點個數較少，將行首碎紙片和行尾碎紙片分別固定在第一個位置和最后一個位置，將尋找全局最小的不匹配問題轉化為旅行商問題，運用改進的遺傳算法進行求解.

針對1.1的情形（2）中碎紙片的拼接：由于訪問點個數是情形（1）的碎紙片個數的至少兩倍，如果直接采用遺傳算法進行求解會造成很大的偏差.為了減少計算復雜度并得到最優解，本文將旅行商問題進行推廣，不僅采用遺傳算法先求初步求解，還設計了一種光學字符識別（OCR）技術檢驗初步解的拼接情況.以兩行混合成類的碎紙片拼接為例，這兩行碎紙片分別含有兩個行首碎紙片（記為行首1，行首2）和兩個行尾碎紙片（記為行尾1，行尾2）.在第1，19，20，38位置依次固定行首1，行尾1，行首2及行尾2碎紙片（或行首1，行尾2，行首2及行尾1碎紙片），共有2種組合.我們對這兩種組合用改進的遺傳算法迭代一定的次數，然后挑選出迭代后距離較短的一種情況保留下來，作為初始拼接情況.采用OCR技術篩選初始拼接的狀況，再次用遺傳算法對拼接錯誤處進行求解.

1.4 組行成頁

當文檔完成所有行內拼接后，每行碎紙片看成一個新的碎紙條，先通過上端和下端較多的空白來確定行首碎紙條和行尾碎紙條.根據上下兩個碎紙條的下基線間的高度基本為間距行高和四線格高度之和的整數倍這一準則，得到碎紙條的排列，完成碎紙片的拼接.

2 碎紙片的拼接算法

2.1 圖像預處理

將碎紙片圖像轉化為灰度值矩陣A（k），k＝1，2，…，209，由于文字的邊緣輪廓是灰色的，避免這部分元素對確定行距高度等產生干擾，運用公式（1）對A（k）的元素進行二值化處理得到，那么由構成的矩陣B（k）的元素僅為0和1，即碎紙片圖像僅含黑白二色.

2.2 文檔分類

先尋找碎紙片的下基線，從而實現文檔分類，具體步驟如下：Step1：設一個維度為row的列向量α（k）的第i個元素值是大小為row×col的二值矩陣B（k）第i行中經過的墨跡數，其計算如公式（2）所示

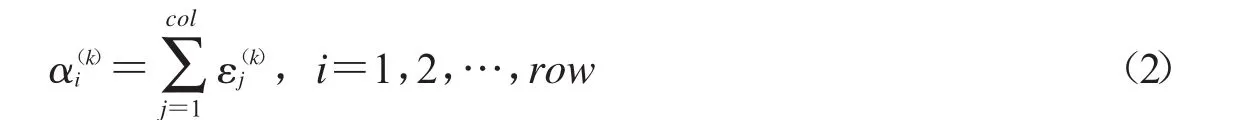
其中

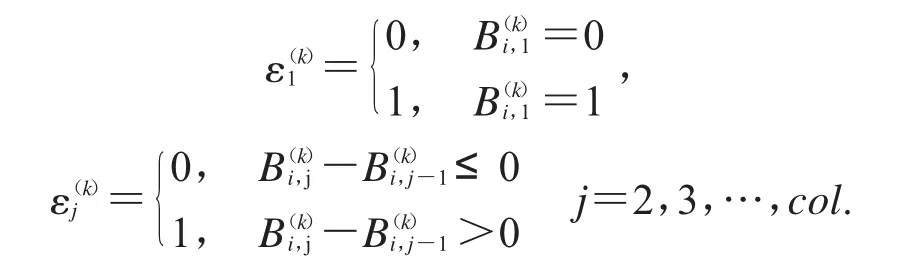
Step2：設一個維度為row的列向量β（k）的第i個元素為C（k）的第i個元素的等級劃分，如圖3所示，其計算如公式（3）所示

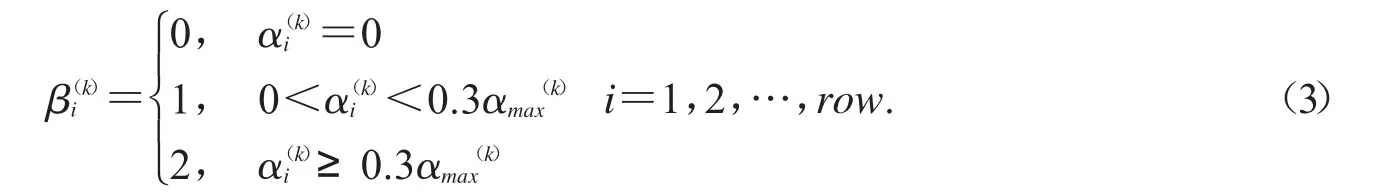
圖3 像素等級劃分

Step3：記四格線的上、中、下部和間距的像素點高度分別為highup，highmid，highlow和highgap.利用游程思想，計算出β（k），k＝1，2，…，209的局部分量全為 0，全為 1，全為 2的長度，再取各長度的眾數分別作為highgap，highup（highlow）和highmid的值.四格線高度及間距高度之和記為hightotal，其計算如公式（4）所示

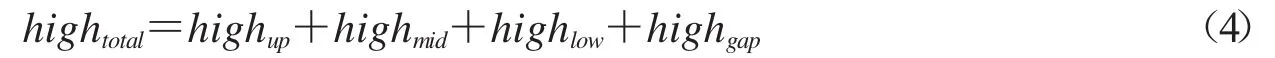
Step4：從上往下搜索β（k）向量，直到其局部向量元素全為2且長度至少為highmid判斷出其表示中部，取其下界作為下基線的位置base（k）.針對少部分β（k）向量沒有局部向量元素全為2且長度至少為highmid的情況，同樣從上往下搜索β（k）向量，直到其局部分量全為1且長度至少為highmid，若其長度近似為highmid，取其下界作為下基線的位置base（k）；若其長度近似為highmid＋highup且其上部分比下部分的值小，取其下界作為下基線的位置base（k）；若其長度近似為highmid＋highup且其下部分比上部分的值小，取其highmid對應的位置作為下基線的位置base（k）；記最小下基線的位置為base（k）min，其計算如公式（5）所示

Step5：利用同行碎紙片下基線基本相同的原理及每一行固定的碎紙片數目的整數倍進行分類.例如，下基線位置為19的碎紙片個數為18，而位置為20的碎紙片個數為1，則它們處于同一類；下基線位置為40的碎紙片個數為17，位置為41的碎紙片個數為19，位置為42的碎紙片個數為2，則它們處于同一類.

2.3 行首和行尾的確定

根據頁邊距尋找出行首和行尾碎紙片，具體步驟如下：

Step1：設一個維度為col的行向量γ（k）的第j個元素為大小為row×col的二值矩陣B（k）第j列有無墨跡的情況，其計算如公式（6）所示

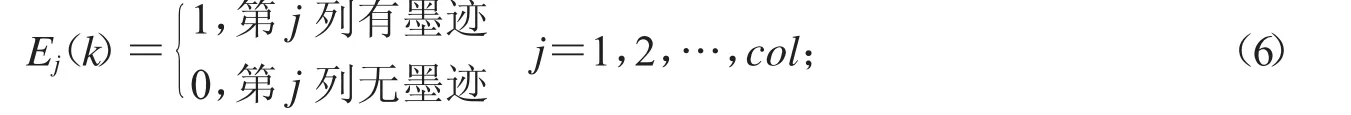
Step2：先確定每一類中碎紙片的行數n，然后挑選出E（k）左端向量0元素最多的n個碎紙片作為行首碎紙片，挑選出E（k）右端向量0元素最多的n個碎紙片最為行尾碎紙片.

2.4 行內拼接

2.4.1 碎紙片之間的距離

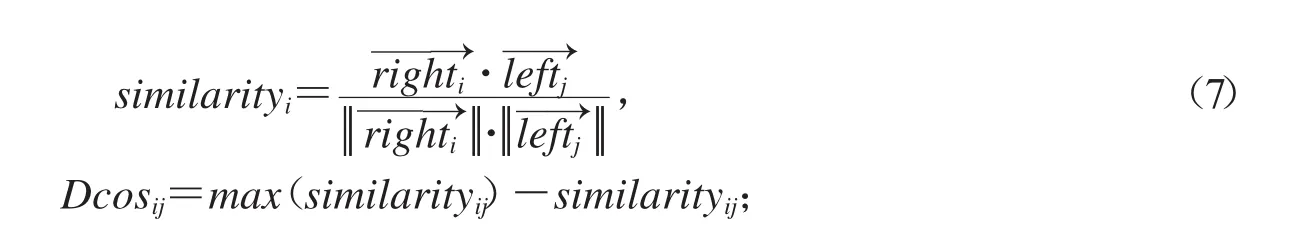
記第i個碎紙片和第j個碎紙片之間的有向不匹配距離為Dmisij，其計算如式（8）所示：

2.4.2 改進遺傳算法（GA）

遺傳算法是一種求解最短路的算法，為了使之能夠處理碎紙片拼接轉化為的旅行商問題，基于文獻[8]，本文對傳統的遺傳算法的交叉，變異，內部交換中做了改進，改進的如下：

1）交叉操作

采用部分映射雜交，確定交叉操作的父代，將父代樣本兩兩分組，每組重復以下過程（方便起見假定單行碎片數為10）：

a.產生兩個隨機整數r1，r2∈[2，9]確定兩個位置，對兩個位置間中間元素進行交叉，如 r1＝4，r2＝7：

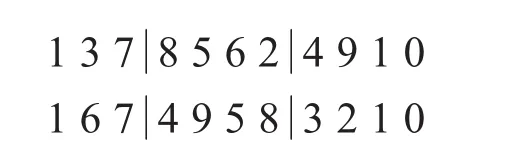
交叉為：

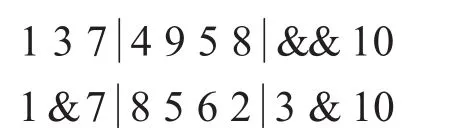
b.交叉后同一條染色體中有重復碎片編號的，不重復的編號進行保留，有沖突的數字（&位置）采用部分映射來消除沖突，即利用中間段的對應關系進行映射，結果為：

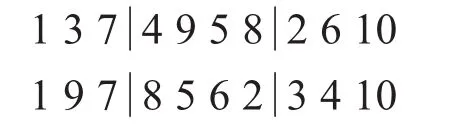
2）變異操作

變異操作采取隨機選取r1，r2∈[2，9]中的兩個位置，將其中的元素對換.如隨機選取位點 r1＝4，r2＝7：

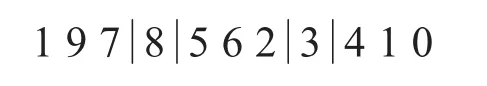
變異后為：

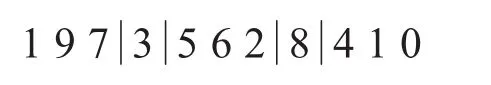
3）內部交換操作

隨機選取 r1，r2，r3∈[2，9]，3個位點，將r1與 r2之間的元素和 r2與 r3之間的元素對換，例如隨機選取 r1＝2，r2＝5，r3＝8：

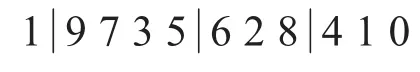
內部交換后的結果為：

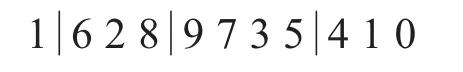
2.4.3 光學字符識別（OCR）

光學字符識別是一種能夠識別出圖像文本內容的技術.為了減少計算復雜度并得到最優解，本文自制OCR技術檢驗拼接口處字母是否完整正確，從而判斷碎紙片是否拼接正確.實現OCR技術的步驟如下：

1）制作字典

首先對文字進行自動化切割.切割時采用先橫切，后縱切，再橫切去除空白的流程進行操作，使得每個字母都處于最小的矩形中，一個切割的例子如圖4所示.切割獲取現有的完整字母，提取不同字母制成字典.為了減少計算復雜度并得到最優解，引入光學字符識別（OCR）技術來對連接處的正確狀況進行判斷.

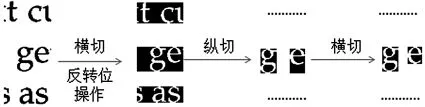
圖4 文字切割流程

2）建立模型

由于切割后即便相同的字母也并不完全相同，所以考慮字母圖像像素點的凈相似率f1和形狀相似度f2，其計算分別如公式（9），（10）所示：

其中d為切割后字母的像素點寬度，h為像素點高度，p為墨跡像素點總個數.假設拼接處有三行文字，設iscorrect表示是否通過OCR檢驗的檢驗量，則評價規則為：

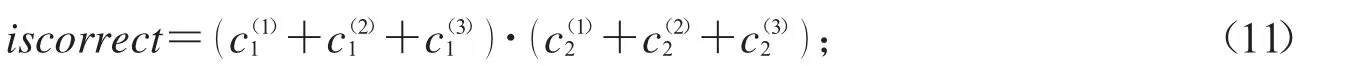
當iscorrect＞0時，通過檢驗，則判斷拼接處正確；

當iscorrect＝0時，不通過檢驗，則判斷拼接處錯誤.

2.4.4 針對一行碎紙片混合的拼接

針對一行碎紙片混合的拼接問題，本文將其轉化為旅行商問題，然后采用遺傳算法求解.在改進的遺傳算法中，固定第一個位置為行首碎紙片，最后一個為行尾碎紙片.由于不匹配距離收斂速率比余弦距離收斂速率大，因此采用不匹配距離作為遺傳算法中的距離，迭代300次，尋找余下碎紙片的全局最優排列.

2.4.5 針對兩行以上碎紙片混合的拼接

針對多行碎紙片混合的拼接問題，本文將其轉化為廣義上的旅行商問題，不但固定第一個（行首）和最后一個紙片（行尾），還在中間固定余下的行首和行尾.然后采用改進的遺傳算法先求初始解，再用OCR技術檢驗拼接處，將不通過的拼接處再次切開，再以余弦距離為遺傳算法中的距離進行迭代得到最終的結果.

在本例中針對兩行混合的碎紙片，需要拼接的紙片一行有38個碎片，因此我們固定的為第1，19，20，38號位置.在兩行混合的紙片中，行首和行尾共有2種組合，本文分別使用兩種組合進行拼接，分別迭代5000次后，最后選取距離最小的組合保留下來作為初步解.本文再采用OCR技術檢驗出初步解的情況，把認為錯誤處再切割開并將認為正確的連接合并成塊，例如圖5所示.再采用遺傳算法，以余弦距離作為距離迭代50次，得到最終解.

圖5 OCR結果

2.5 組行成頁

當文檔完成所有行內拼接后，每行可看成一個新的碎紙條，通過上端和下端較多的空白來確定行首碎紙條和行尾碎紙條.

下面是排列除行首碎紙條和行尾碎紙條剩余的碎紙條的算法：

1）設第i個碎紙條的最小下基線的位置為baseline（i）min第j個碎紙條的最小下基線的位置為baseline（j）min，第j個碎紙片要與第i個碎紙片之間字母行數n的數學表達式如下：

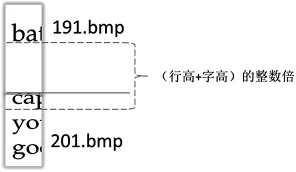
圖6 基線距離

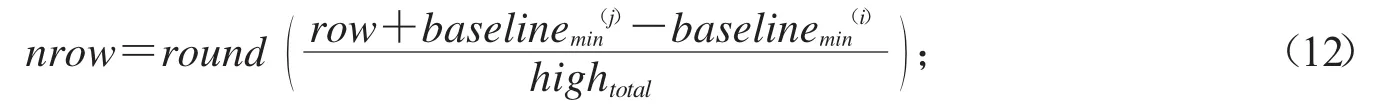
其中round表示四舍五入運算法.

2）第j個碎紙片要與第i個碎紙片匹配時，baselinej應該滿足：

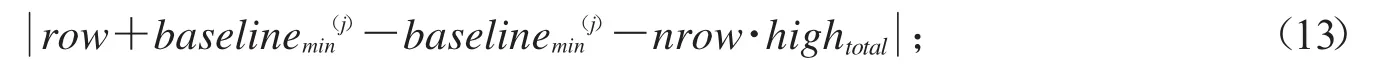
取值最小.其中row是碎紙條對應二值矩陣的行數.

3）如果滿足與第i個碎紙片匹配的碎紙條j有多個時，定義gi，j為第i個碎紙條下邊界和第j個碎紙條上邊界的不匹配距離，即：

其中n為每一行碎紙片含有碎紙片的個數.

選取與第i個碎紙片不匹配距離最小的第j個碎紙片.

2.6 拼接試驗

最后從拼接結果看，英文文檔碎紙片在行分類時由于處于不同行的碎紙片下基線相近，所以有部分分類中含有兩行碎紙片混搭的.針對這類問題，本文不僅將原來改進的遺傳算法進行拓展，還設計了適用于檢測邊緣字母是否正常的OCR技術，來挑選拼接錯誤的碎紙片.由于本文設計的OCR較為嚴格，會將少量拼接正確的碎紙片誤認為錯誤的，但是其能夠將所有拼接錯誤的碎紙片尋找出來，因此不會影響拼接結果.在組行成頁步驟中，由于較多是橫切到行距的，所以采用貪婪算法及遺傳算法都得不到好結果，所以采用基于基線的算法是行之有效的.從試驗結果看，本文設計來解決英文碎紙片拼接的算法是有效的.

3 模型的推廣

3.1 中文拼接

中文文字的高度基本一致，文字中間水平的線的差異較小.本文定義中心線為文字中間水平的線，如圖5所示.根據同行文字的中心線基本一致，建立基于最小中心線確定碎紙片行分類的算法.再用改進的遺傳算法，采用有向余弦距離，求解有中文碎紙片作為訪問點的旅行商問題.在組行成頁中，為了減少誤差，利用中文文字的高度基本一致這一準則，把碎紙片拼接分成兩種類型：

（1）針對橫切到文字的碎紙條，根據上邊碎紙條被切字體余下高度和下邊碎紙條被切字體余下高度之和基本等于字體高度的準則，如圖8所示，設第i個碎紙條最下部分黑色像素高為，第j個碎紙條最上邊黑色像素高為，第i個碎紙條要與第j個碎紙條匹配時，需要滿足以下式子：

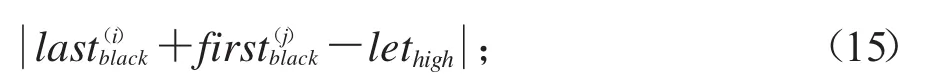
取值最小，其中lethigh表示文字像素高.

（2）針對橫切到空白間隔的碎紙條，根據上邊碎紙條被切空白間隔剩余的高度和下邊碎紙條被切空白間隔剩余的高度之和基本等于字體高度的準則，如圖9所示，設第i個碎紙條最下部分黑色像素高為last（i）white，第j個碎紙條最上邊白色像素高為first（j）white，第j個碎紙條要與第i個碎紙條匹配時，first（j）white需要滿足式子（16）：

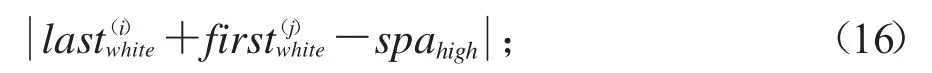
取值最小，其中spahigh表示行距像素高.

3.2 拼接試驗

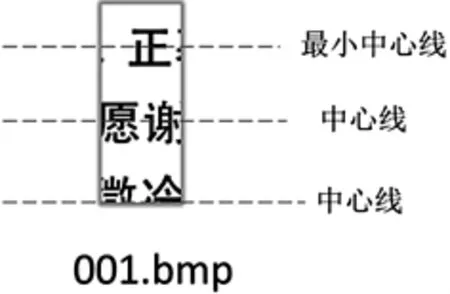
圖7 中心線

圖8 文字高度

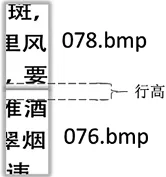
圖9 間距特征

由于中文文檔各行碎紙片的中心線不同，所以能夠實現行分類，即每一類中含每一行混合的碎紙片.本文在遺傳算法中分別采用余弦距離和不匹配距離作為距離求解旅行商問題.對比發現，以不匹配距離為距離求解出來的最優解不一定是最佳解，即求解出來的最短距離經過的點的順序對應的碎紙片序號拼接是不正確的；余弦距離作為距離求解出來的最優解是最佳解.在最后為了減少中心線間隔較遠帶來的誤差，本文利用字高和間距基本不變的原理實現組行成頁.試驗結果表明，本文設計的算法針對中文文檔碎紙片拼接也是有效的.

4 結語

本文消除了英文碎紙片中字母高度不同的干擾，找出了碎紙片的最小下基線，合理地利用最小下基線對碎紙片進行分類；將分類結果的拼接問題轉化為旅行商問題，采用改進的遺傳算法和自制的OCR技術對其進行求解；最后再次利用下基線，且以貪婪算法為輔，對碎紙條進行拼接.在文章最后進行仿真分析，采用本文提出的算法對209張英文碎紙片進行全自動拼接，無需人為干預.再結合中文文字的特點，對適用于英文碎紙片拼接的算法進行修改：在分類中采用中心線，而行內拼接中由于中文邊界信息量較大所以無需OCR技術，在組行成頁中利用字高及間距進行拼接得到適用于中文碎紙片拼接的算法，同樣可對209張中文碎紙片進行全自動拼接，無需人為干預.本文設計的算法僅對規則碎紙片的拼接有效，對于一些不規則的碎紙片，本文還是需要對算法進行修改，這是進一步研究的問題.

致謝：感謝李健老師的悉心指導.

[1]羅智中.基于文字特征的文檔碎紙片半自動拼接[J].計算機工程與應用，2012，48（5）：207-210.

[2]劉鐵.基于數字圖像的碎紙復原模型與算法——2013年全國大學生數學建模B題碎紙片的拼接復原問題[J].重慶理工大學學報（自然科學版），2015，27（3）：83-88.

[3]馬俊明，賴楚廷，卜尚明，等.基于文字特征的規則碎紙片自動拼接[J].汕頭大學學報（自然科學版），2014，29（2）：4-10.

[4]金明婭，孫丹蕾，趙艷，等.單面英文碎紙片的拼接復原及算法實現[J].延安大學學報（自然科學版），2015，34（1）：14-18.

[5]周一凡，王松靜，黃永斌.英文字母特征的雙面碎紙拼接[J].中國圖象圖形學報，2015，20（1）：85-94.

[6]張亮.基于聚類優化模型的碎紙自動拼接方法研究[J].計算機應用與軟件，2015，32（12）：218-221.

[7]2013年全國大學生數學建模競賽B題附件3和附件4的數據[EB/OL].（2013-09-13）[2017-02-25].http：//www.mcm.edu.cn/problem/2013/2013.html.

[8]郁磊，史峰，王輝，等.MATLAB智能算法30個案例分析[M].北京：北京航空航天大學出版社，2011.