催化裂化MIP工藝原料油聚類研究

歐陽福生，李 盾，方偉剛

(華東理工大學(xué)石油加工研究所，上海 200237)

催化裂化是重油輕質(zhì)化的主要工藝。我國(guó)催化裂化裝置所生產(chǎn)的汽油和柴油約占成品汽油和柴油總量的70%和30%[1]。實(shí)際生產(chǎn)過程中，催化裂化主要以餾分油和渣油為原料，其中餾分油主要為直餾減壓餾分油，也包括少量焦化蠟油，渣油主要為減壓渣油、加氫處理渣油或脫瀝青油等，并以一定比例摻入餾分油中進(jìn)行加工。因催化裂化原料油種類和渣油摻煉比例的不同，原料油性質(zhì)會(huì)發(fā)生較大變化。如果對(duì)不同原料油的加工不加以區(qū)分，僅憑借生產(chǎn)經(jīng)驗(yàn)進(jìn)行操作就會(huì)使大部分原料油難以達(dá)到最優(yōu)的加工狀態(tài)。聚類分析[2]是比較各個(gè)事物之間的性質(zhì)，并將性質(zhì)相似的歸于一類，將性質(zhì)差別較大的歸入不同的類別中，與平常所說的“物以類聚”相仿。聚類分析是數(shù)據(jù)挖掘的一項(xiàng)重要功能，它不需要事先確定分類的準(zhǔn)則來分析數(shù)據(jù)對(duì)象，而是在訓(xùn)練數(shù)據(jù)的過程中根據(jù)最大的組內(nèi)相似性和最小的組間相似性為原則進(jìn)行聚類和分組。在實(shí)際過程中，可以將一個(gè)類別中的數(shù)據(jù)對(duì)象作為一個(gè)整體來處理，因此，聚類分析在許多領(lǐng)域得到廣泛應(yīng)用[3-5]。傳統(tǒng)的聚類算法主要包括劃分聚類方法和層次聚類方法，劃分聚類方法主要的算法有K-means算法、K-medoids算法、CLARA算法和CLARANS算法[6]。層次聚類的方法有BRICH算法、CHAMELEON算法、ROCK算法和CURE算法[7-8]。除此之外，傳統(tǒng)的聚類算法還有基于網(wǎng)格的聚類、基于圖論的聚類、基于模型的聚類、機(jī)器學(xué)習(xí)中的聚類算法和高維數(shù)據(jù)的聚類算法等[9-10]。除了上述傳統(tǒng)聚類算法外，還有模糊聚類算法、綜合聚類算法和新對(duì)象的聚類算法[11]，這些聚類算法對(duì)傳統(tǒng)聚類算法進(jìn)行了擴(kuò)展，使得它們具有更強(qiáng)的適用性。

MIP工藝是由中國(guó)石化石油化工科學(xué)研究院開發(fā)，通過對(duì)催化裂化氫轉(zhuǎn)移反應(yīng)的調(diào)控，直接降低催化裂化汽油烯烴含量，同時(shí)多產(chǎn)異構(gòu)烷烴的催化裂化新工藝[12]。本研究在綜合分析MIP裝置原料油數(shù)據(jù)的基礎(chǔ)上，以汽油收率最大為目標(biāo)，通過建立原料油數(shù)據(jù)的聚類評(píng)價(jià)模型，旨在將性質(zhì)最為相近的原料油聚為一類，并對(duì)每一類原料油的特征進(jìn)行描述，以此為基礎(chǔ)，有助于建立相應(yīng)的智能化模型，尋找加工該類別原料油時(shí)目的產(chǎn)物收率最大的操作條件。

1 數(shù)據(jù)收集

原料油性質(zhì)是決定催化裂化產(chǎn)品的基礎(chǔ)。原料油為烷烴、烯烴、環(huán)烷烴和芳烴的混合物，其中烷烴發(fā)生分解反應(yīng)；烯烴除發(fā)生分解反應(yīng)外還發(fā)生氫轉(zhuǎn)移、異構(gòu)化、芳構(gòu)化反應(yīng)；環(huán)烷烴主要開環(huán)斷裂生成烯烴或通過氫轉(zhuǎn)移轉(zhuǎn)化為芳烴；芳烴的烷基側(cè)鏈容易發(fā)生斷裂生成烯烴。一般認(rèn)為原料油中支鏈烷烴、烯烴、環(huán)烷烴、帶側(cè)鏈芳烴的含量越高，其裂解性能越好，越有利于生成C5～C12汽油組分。因而，原料中各烴類含量對(duì)于反應(yīng)速率的影響較大。原料油中含有的金屬會(huì)引起催化劑的失活，主要影響反應(yīng)的金屬包括鎳、釩、鐵以及鈣。催化裂化反應(yīng)條件下，鎳起脫氫的作用，使催化裂化產(chǎn)物生成多環(huán)芳烴聚合物和焦炭，使催化劑的選擇性變差；釩會(huì)破壞分子篩中的晶體結(jié)構(gòu)并使催化劑的活性下降。殘?zhí)糠从吃现猩刮镔|(zhì)含量的多少和生焦傾向，殘?zhí)吭酱螅固慨a(chǎn)率越高。因此，殘?zhí)恳彩且粋€(gè)重要的影響因素。

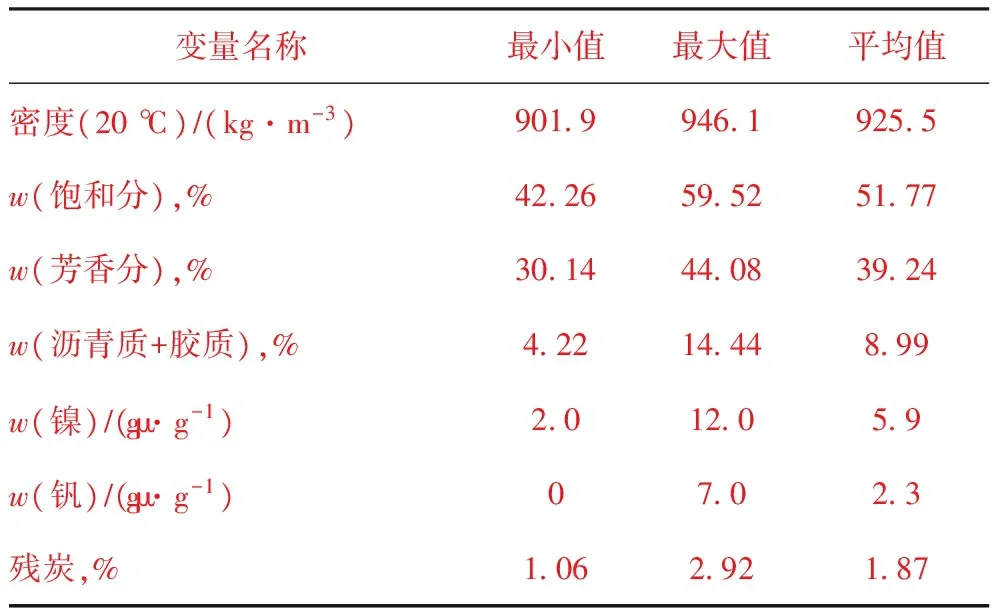
表1 原料油性質(zhì)分布

2 原料油聚類模型的建立

K-means算法理論可靠、算法簡(jiǎn)單并且收斂速率快，除此之外該算法對(duì)大數(shù)據(jù)集有較高的效率，因此K-means算法作為一種基本的劃分算法被廣泛應(yīng)用于數(shù)據(jù)挖掘領(lǐng)域[13]。模糊聚類算法可以得到每個(gè)樣本屬于各個(gè)類別的不確定程度，表達(dá)了樣本類屬的中介性，建立了樣本屬于各個(gè)類別的不確定程度，因此模糊聚類算法在聚類分析中的應(yīng)用也比較廣泛[14]。本研究分別采用K-means算法和模糊聚類算法建立原料油性質(zhì)的聚類模型，采用MATLAB作為原料油性質(zhì)聚類模型的編程平臺(tái)。

2.1 K-means算法聚類

2.1.1K-means算法K-means算法是在給定聚類數(shù)k時(shí)，通過最小化組內(nèi)誤差平方和得到每一個(gè)樣本點(diǎn)的分類。在使用時(shí)首先隨機(jī)選擇k個(gè)對(duì)象作為初始k個(gè)類的質(zhì)心，然后對(duì)剩余的每個(gè)對(duì)象，根據(jù)其與各個(gè)質(zhì)心的距離，將它賦給最近的類別，然后重新計(jì)算每個(gè)類別的質(zhì)心。K-means算法在應(yīng)用時(shí)通常采用歐式距離來計(jì)算對(duì)象與質(zhì)心距離，計(jì)算式如(1)所示。

(1)

式中，xik、xjk分別表示第i和第j個(gè)數(shù)據(jù)對(duì)象在屬性k上的取值。

數(shù)據(jù)對(duì)象和質(zhì)心的距離會(huì)不斷重復(fù)的計(jì)算，直到準(zhǔn)則函數(shù)收斂，通常采用的準(zhǔn)則函數(shù)為平方誤差和準(zhǔn)則函數(shù)，即SSE(sum of the squared error)：

(2)

式中：SSE為數(shù)據(jù)集中所有對(duì)象的平方誤差總和；p為數(shù)據(jù)對(duì)象；K-means算法將觀測(cè)樣本分為i個(gè)集合C= {C1，C2，…，Ci}；mi為集合Ci的平均值。這個(gè)準(zhǔn)則函數(shù)使得生成的結(jié)果盡可能緊湊和獨(dú)立。

K-means算法的具體過程如下：

(1)給定大小為n的數(shù)據(jù)集，令I(lǐng)=1，選取k個(gè)初始聚類中心Zj(I)，j=1，2，3，…，k。

(2)計(jì)算每個(gè)數(shù)據(jù)對(duì)象與聚類中心的距離D(xi，Zj(I))，i=1，2，3，…，n，j=1，2，3，…，k，如果滿足：

D(xi，Zk(I))=min{D(xi，Zk(I))，
i=1，2，3，…，n}

(3)

則xi∈Ck。

(3)計(jì)算k個(gè)新的聚類中心：

(4)

以便下一步進(jìn)行判斷。

(4)判斷：Zj(I+1)≠Zj(I)，j=1，2，3，…，k，則I=I+1，返回(2)；否則算法結(jié)束。

2.1.2K-means聚類結(jié)果分析K-means聚類的最佳聚類數(shù)kopt事先無法確定，目前許多學(xué)者已經(jīng)提出一些確定kopt的有效方法[15-16]，但是由于這些方法中的構(gòu)造函數(shù)自身存在缺陷，一般難以通過這些方法直接確定kopt。一般情況下，可以先確定聚類數(shù)的最小和最大值，然后在該范圍內(nèi)進(jìn)行試算，計(jì)算結(jié)果最符合實(shí)際過程的聚類數(shù)即為最佳聚類數(shù)。本研究設(shè)定最小聚類數(shù)kmin=3，最大聚類數(shù)采用經(jīng)驗(yàn)式(5)[17]計(jì)算。

(5)

式中，n表示聚類的樣本數(shù)，由于原料油性質(zhì)共95組樣本，因此kmax=9。

將95組包含ρ，SH，AH，AR，Ni，V，CR的原料油數(shù)據(jù)進(jìn)行歸一化計(jì)算，計(jì)算式如式(6)所示。

(6)

式中：xi表示屬性i的平均值；si表示屬性i的標(biāo)準(zhǔn)差；xij表示屬性i的第j組樣本原始值；zij表示屬性i的第j組樣本標(biāo)準(zhǔn)化值。

聚類數(shù)從3依次變化至9，并設(shè)定最大迭代次數(shù)為80。使用MATLAB編好的程序進(jìn)行原料油數(shù)據(jù)的聚類分析，計(jì)算結(jié)果如表2所示。

表2 變量貢獻(xiàn)度分布表

表2是聚類數(shù)在3～9變化的過程中，各變量對(duì)聚類結(jié)果貢獻(xiàn)度排列情況。因?yàn)榫垲惖哪康氖钦业矫恳活愒嫌?智能化模型)在汽油收率最大的同時(shí)盡可能控制生焦量的操作條件。因此，聚類過程中應(yīng)以影響汽油收率和生焦量的因素為主。汽油的生成主要是因?yàn)橥闊N發(fā)生分解反應(yīng)，烯烴發(fā)生裂化、氫轉(zhuǎn)移和異構(gòu)化反應(yīng)，環(huán)烷烴發(fā)生斷裂生成烯烴，芳烴的烷基側(cè)鏈發(fā)生斷裂生成烯烴等一系列反應(yīng)；焦炭一般是多環(huán)芳烴的縮合結(jié)構(gòu)，芳烴在側(cè)鏈基團(tuán)斷裂后具有強(qiáng)烈的生焦傾向，而瀝青質(zhì)和膠質(zhì)中也含有大量的多環(huán)芳烴和雜環(huán)芳烴。因此影響汽油收率的因素主要是SH和AH，其中SH對(duì)汽油的貢獻(xiàn)最大；影響焦炭收率的主要因素是AH和AR，其中AR是主要影響因素。ρ從一定程度上表示原料的輕重程度，ρ越大，AR和AH越大，SH越小；反之，AR和AH越小，SH越大。CR是表示生焦傾向的一個(gè)重要指標(biāo)，CR越大，表明原料在反應(yīng)時(shí)越容易生焦。Ni和V在反應(yīng)過程中主要影響催化劑的活性和使用壽命，一定程度上促進(jìn)焦炭的生成，而在實(shí)際生產(chǎn)過程可以通過加入新鮮催化劑和金屬鈍化劑來保持催化劑活性在指標(biāo)范圍內(nèi)。因此，重金屬含量可以作為次要的因素考慮。綜上所述，當(dāng)聚類數(shù)為4時(shí)，各變量對(duì)聚類結(jié)果影響的重要性由大到小的順序?yàn)椋篠H>AR>AH>ρ>CR>Ni>V，滿足上述的分析過程，因此確定最佳聚類數(shù)kopt=4。

表3為當(dāng)聚類數(shù)為4時(shí)，每一類每個(gè)變量的平均值。當(dāng)原料油飽和分含量越高時(shí)，芳香分含量和(瀝青質(zhì)+膠質(zhì))含量越低，原料油密度越小，殘?zhí)吭叫　５谝活愒嫌兔麨椤俺刭|(zhì)原料油”，其特點(diǎn)是芳香分含量和(瀝青質(zhì)+膠質(zhì))含量、殘?zhí)俊㈡嚭外C的含量最高，殘?zhí)恳沧罡摺Ｔ诜磻?yīng)過程中，該類油所產(chǎn)汽油收率很低，生焦量很高，高的燒焦負(fù)荷和高的重金屬含量大大縮短了催化劑的使用壽命，能耗也高，因此這類油煉制成本較高。第二類原料油命名為“重質(zhì)原料油”，該類油比第一類油飽和分含量高，但是由于(瀝青質(zhì)+膠質(zhì))含量也比較高，使得殘?zhí)枯^高，此外重金屬含量也較高，這類油所產(chǎn)汽油收率會(huì)比第一類油高，但是生焦量也會(huì)很大。第三類原料油命名為“超輕質(zhì)原料油”，這類油的特點(diǎn)是飽和分含量最高，芳香分和瀝青質(zhì)、膠質(zhì)總含量很低，同時(shí)鎳和釩的含量也很低，這類油加工的經(jīng)濟(jì)效益最高。第四類原料油命名為“輕質(zhì)原料油”，這類油的特點(diǎn)是飽和分含量較高，芳香分和瀝青質(zhì)、膠質(zhì)總含量較低，同時(shí)鎳和釩的含量也較低。

表3 當(dāng)聚類數(shù)為4時(shí)每一類變量的平均值

以對(duì)汽油收率貢獻(xiàn)大的飽和分含量為橫坐標(biāo)，對(duì)焦炭收率貢獻(xiàn)大的(瀝青質(zhì)+膠質(zhì))含量為縱坐標(biāo)，繪制了95組樣本的散點(diǎn)圖(圖1)。由圖1可以看出，每一類與其它類的邊界較為明顯，分類效果較好。

圖1 K-means聚類散點(diǎn)圖■—第一類油; ●—第二類油； ★—第三類油； 第四類油

2.2 模糊c均值聚類

K-means聚類分析是一種硬劃分，它把每個(gè)待辨識(shí)的對(duì)象嚴(yán)格地劃分到某個(gè)類中，具有非此即彼的性質(zhì)。因此，K-means的每一類都具有明確的界限。而實(shí)際上有些對(duì)象并沒有嚴(yán)格屬性，它們?cè)谛螒B(tài)類屬方面存在著中介性，于是人們開始使用模糊的方法來處理聚類問題，稱之為模糊聚類分析。模糊劃分的概念最早由Ruspini在1969年提出的[18]，它是指某些對(duì)象或者概念并沒有嚴(yán)格的屬性，它們?cè)谛螒B(tài)和類屬方面存在著中介性，利用這一概念人們提出了多種聚類方法，其中應(yīng)用最廣泛的是模糊c均值聚類算法(FCM，F(xiàn)uzzy c-means)。

FCM在計(jì)算時(shí)給定數(shù)據(jù)集X={x1，x2，……，xn}，其中每個(gè)元素包含s個(gè)屬性。模糊聚類就是要把X劃分為c類(2≤c≤n)，v={v1，v2，……，vc}為c個(gè)聚類中心。在FCM中，每一個(gè)樣本點(diǎn)不是嚴(yán)格地被劃分到某一類，而是以一定的隸屬度屬于某一類。令μij表示第j個(gè)樣本點(diǎn)屬于第i類的隸屬度，μij∈[0，1]，數(shù)據(jù)對(duì)象的隸屬度總和為1。

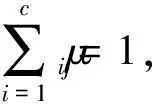
(7)

FCM的目標(biāo)函數(shù)為：

(8)

式中：dij=‖xj-vi‖，為樣本點(diǎn)xj與聚類中心vi之間的歐幾里德距離；m∈[1，∞)]是模糊加權(quán)指數(shù)，通常m=2。

構(gòu)造如下新的目標(biāo)函數(shù)，可求得使式(8)達(dá)到最小值的必要條件：

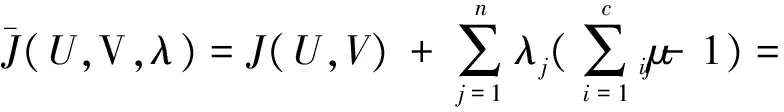
(9)

式中λj(j=1，2，……，n)是式(7)的n個(gè)約束式的拉格朗日算子。對(duì)輸入變量進(jìn)行求導(dǎo)，使式(8)達(dá)到最小的必要條件為：

(10)

(11)

有上述兩個(gè)必要條件，F(xiàn)CM算法就變成了一個(gè)簡(jiǎn)單地迭代計(jì)算過程。在批處理方式下，F(xiàn)CM通過以下步驟來確定聚類中心ci和隸屬矩陣U：步驟1，初始化隸屬矩陣U，其值是[0，1]間的隨機(jī)數(shù)并且滿足式(7)中的約束條件；步驟2，用式(10)計(jì)算各個(gè)聚類的中心，記為ci，i=1，2，……，c；步驟3，根據(jù)式(8)計(jì)算目標(biāo)函數(shù)的值，如果函數(shù)值小于預(yù)先設(shè)定的閥值，或它與上一次目標(biāo)函數(shù)的差值的絕對(duì)值小于閥值，則算法停止；步驟4，用式(11)計(jì)算新的U矩陣，返回步驟2。

2.3 模糊c均值聚類結(jié)果

FCM聚類算法最重要的任務(wù)是確定最佳聚類數(shù)，現(xiàn)有的算法需要預(yù)先確定聚類的數(shù)目，但是實(shí)際問題中由于樣本數(shù)量巨大，很難有效確定聚類數(shù)目。聚類有效性函數(shù)能夠通過找到函數(shù)的極值達(dá)到對(duì)聚類數(shù)c的優(yōu)選，而常用的有效性函數(shù)一般是基于隸屬度的有效性函數(shù)，包括劃分系數(shù)F(U，c)、可能性劃分系數(shù)P(U，c)和聚類有效性函數(shù)P(U，c)[19]。對(duì)于給定的聚類數(shù)c和隸屬度矩陣U：

(12)

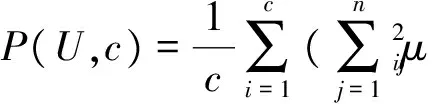
(13)

式中，n為聚類樣本個(gè)數(shù)。

FP(U，c)=F(U，c)-P(U，c)

(14)

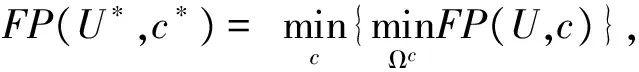
本研究中FCM算法的參數(shù)設(shè)置如表4所示。

表4 FCM算法主要參數(shù)

FCM的最佳聚類數(shù)copt事先無法確定，目前許多學(xué)者已經(jīng)提出一些確定copt的有效方法[15-16]，但是由于這些方法中的構(gòu)造函數(shù)自身存在缺陷，一般難以通過這些方法直接確定copt。一般情況下，可以先確定聚類數(shù)的最小和最大值，然后在該范圍內(nèi)進(jìn)行試算，計(jì)算結(jié)果最符合實(shí)際過程的聚類數(shù)即為最佳聚類數(shù)。本研究設(shè)定最小聚類數(shù)cmin=3，最大聚類數(shù)采用經(jīng)驗(yàn)公式(15)[17]計(jì)算。

(15)

式中，n為樣本個(gè)數(shù)。在式(15)的基礎(chǔ)上，取最大聚類數(shù)cmax=12。FCM聚類有效性函數(shù)值和收斂迭代次數(shù)與聚類數(shù)目的關(guān)系見表5。由表5可以看出，當(dāng)聚類數(shù)為5時(shí)，對(duì)應(yīng)的有效性函數(shù)值最小為0.006 8，因此，F(xiàn)CM算法的最佳聚類數(shù)copt=5。表5為當(dāng)聚類數(shù)為5時(shí)，95組原料油樣本對(duì)于不同類別的隸屬度。由表6可以看出，第1組樣本對(duì)于5個(gè)類別的隸屬度中，對(duì)第1個(gè)類別的隸屬度最大，為0.269 720，說明第1組樣本的原料油性質(zhì)與第1個(gè)類別的原料油性質(zhì)最相近；第3組樣本對(duì)于5個(gè)類別的隸屬度中，對(duì)第3個(gè)類別的隸屬度最大，為0.389 022，說明第3組樣本的原料油性質(zhì)與第3個(gè)類別的原料油性質(zhì)最相近。

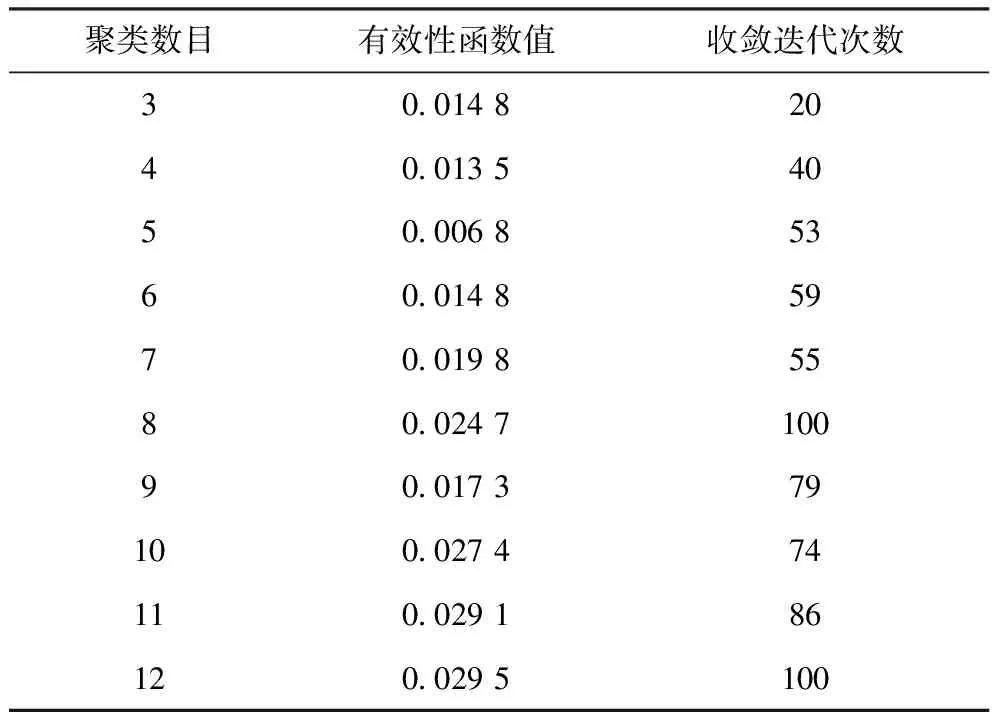
表5 數(shù)據(jù)集分類的有效性函數(shù)值和收斂迭代次數(shù)與聚類數(shù)目的關(guān)系

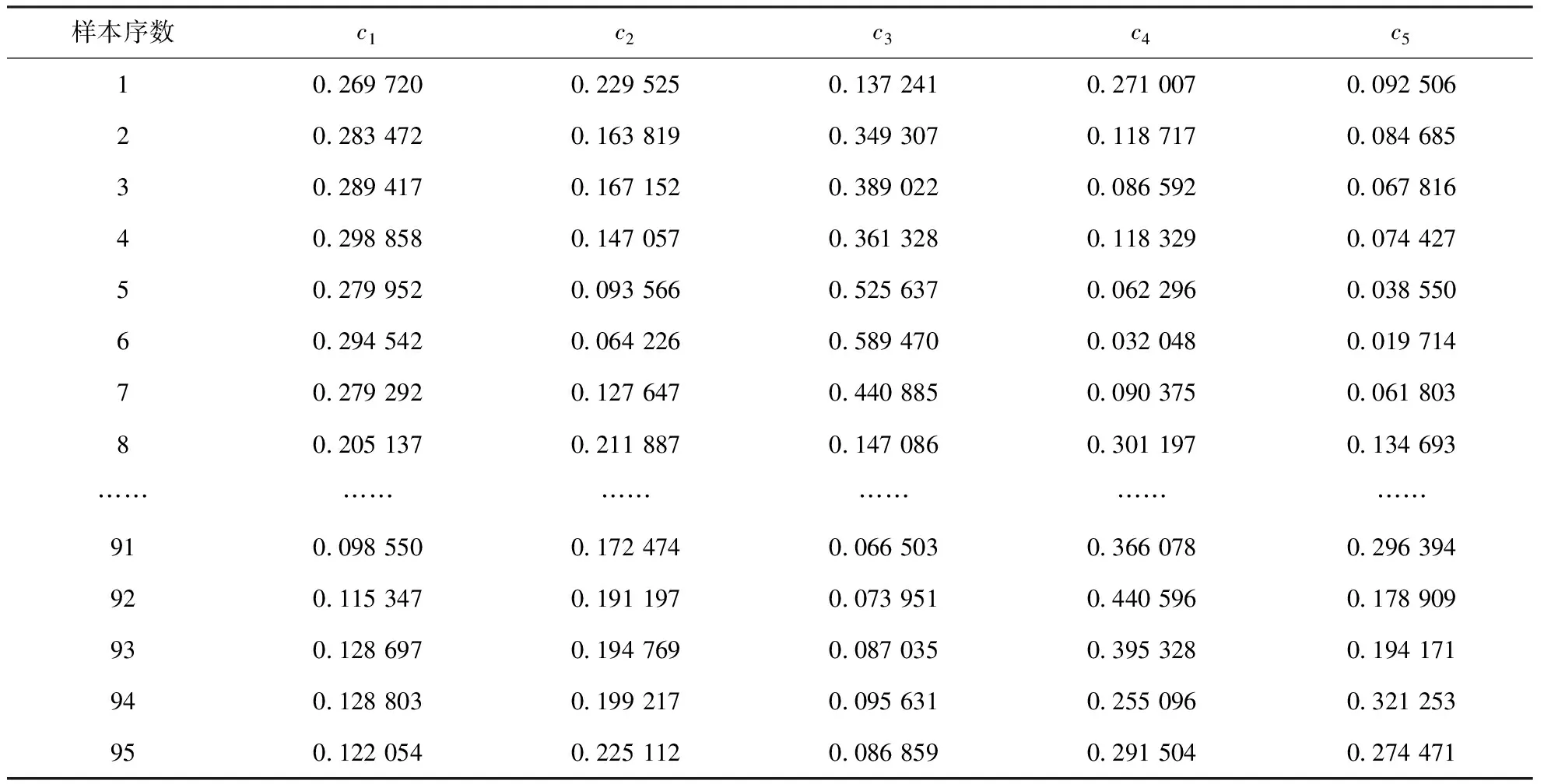
表6 聚類數(shù)為5時(shí)原料油樣本對(duì)于不同類別的隸屬度

表7為當(dāng)聚類數(shù)為5時(shí)，每一類中每個(gè)變量的平均值。由表7可以看出，原料油飽和分含量越高，(膠質(zhì)+瀝青質(zhì))含量越低，原料油密度越小，殘?zhí)吭降汀５谝活愒嫌兔麨椤拜p質(zhì)原料油”，這類油的特點(diǎn)是飽和分含量較高，芳香分和(瀝青質(zhì)+膠質(zhì))含量較低，同時(shí)鎳和釩的含量也較低。第二類和第五類原料油密度相近，(膠質(zhì)+瀝青質(zhì))含量也相近，說明這兩類油輕重程度相似，但是這兩類油重金屬含量不同，第二類重金屬含量明顯低于第五類油，因此可以將第二類油命名為“低金屬重質(zhì)原料油”，第五類原料油命名為“高金屬重質(zhì)原料油”，第二類油的飽和分含量相對(duì)較高，殘?zhí)肯鄬?duì)較低，因此汽油收率相對(duì)于第五類油大，同時(shí)焦炭收率小，催化劑的消耗量較小。第三類原料油命名為“超輕質(zhì)原料油”，這類油的特點(diǎn)是飽和分含量最高，芳香分和(瀝青質(zhì)+膠質(zhì))含量最低，同時(shí)鎳和釩的含量也最低，這類油的經(jīng)濟(jì)效益最高。第四類原料油命名為“超重質(zhì)原料油”，其特點(diǎn)是芳香分含量和(瀝青質(zhì)+膠質(zhì))含量最高，殘?zhí)恳沧罡撸诜磻?yīng)過程中，該類油汽油收率很低，生焦量很高，同時(shí)鎳和釩的含量也最高，催化劑的損耗也最高，因此這類油煉制成本最高。

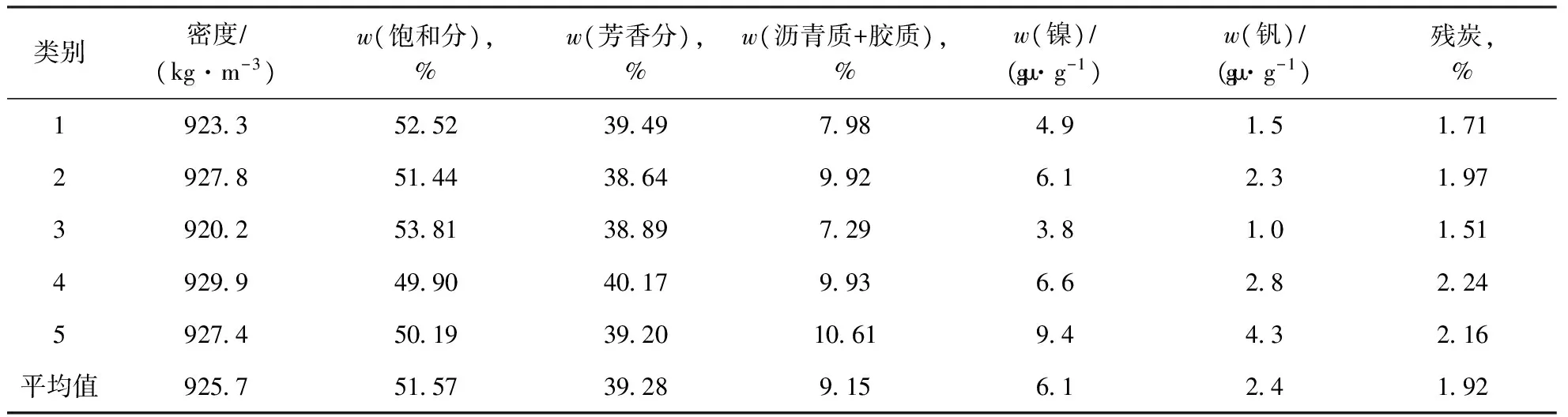
表7 聚類數(shù)為5時(shí)每一類變量的平均值

3 結(jié) 論

以催化裂化MIP裝置工業(yè)數(shù)據(jù)為基礎(chǔ)，選取原料油性質(zhì)中的密度、飽和分含量、芳香分、(瀝青質(zhì)+膠質(zhì))含量、鎳含量、釩含量、殘?zhí)康?個(gè)變量，建立了原料油性質(zhì)的K-means和FCM聚類模型。K-means聚類法將原料油性質(zhì)的95組樣本分為4類，分別為“超重質(zhì)原料油”、“重質(zhì)原料油”、“超輕質(zhì)油”和“輕質(zhì)油”，F(xiàn)CM聚類法將原料油性質(zhì)的95組樣本分為5類，5類油的命名方式是在K-means的基礎(chǔ)上將重質(zhì)原料油分為“低金屬重質(zhì)油”和“高金屬重質(zhì)油”兩類。聚類結(jié)果中的每一類原料油特征都比較明顯，表明K-means和FCM聚類法對(duì)于原料油性質(zhì)的聚類分析均具有較好的適用性。這樣，可以針對(duì)每一類原料油建立相應(yīng)的產(chǎn)品分布優(yōu)化智能模型，從而尋找到使目的產(chǎn)品收率最大的操作條件，對(duì)提高煉油廠的經(jīng)濟(jì)效益具有一定的指導(dǎo)意義。

[1] 許友好. 我國(guó)催化裂化工藝技術(shù)進(jìn)展[J]. 中國(guó)科學(xué)，2014，44(1)：13-24

[2] 周濤，陸惠玲. 數(shù)據(jù)挖掘中聚類算法研究進(jìn)展[J]. 計(jì)算機(jī)工程與應(yīng)用，2012，48(12)：100-111

[3] 楊敬一，鄒華偉，蔡海軍，等. 原料性質(zhì)對(duì)焦化行為的影響[J]. 石油煉制與化工，2015，46(10)：6-11

[4] 魯紅英，肖思和，楊盡. 模糊聚類分析方法在土地整治分區(qū)中的應(yīng)用[J]. 成都理工大學(xué)學(xué)報(bào)：自然科學(xué)版，2014，41(1)：124-128

[5] 周俊，劉麗川，楊繼平. 基于K-均值聚類與小波分析的聲發(fā)射信號(hào)去噪[J]. 石油化工高等學(xué)校學(xué)報(bào)，2013，26(3)：69-73

[6] 黎敏. 數(shù)據(jù)挖掘算法研究與應(yīng)用[D]. 大連：大連理工大學(xué)，2004

[7] 向先全，王海波，路文海，等. 基于數(shù)據(jù)挖掘的渤海灣水生態(tài)環(huán)境特性研究[J]. 海洋通報(bào)，2013，32(1)：72-77

[8] Guha S，Rastogi R，Shim K. Cure：An efficient clustering algorithm for large databases [J]. Information Systems，2001，26(1)：35-58.

[9] 賀玲，吳玲達(dá)，蔡益朝，等. 數(shù)據(jù)挖掘中的聚類算法綜述[J]. 計(jì)算機(jī)應(yīng)用研究，2007，24(1)：10-13

[10] 陳安，陳寧，周龍?bào)J. 數(shù)據(jù)挖掘技術(shù)及應(yīng)用[M]. 北京：科學(xué)出版社，2006：183-203

[11] 馬飛. 數(shù)據(jù)挖掘中的聚類算法研究[D]. 南京：南京理工大學(xué)，2008

[12] 許友好，張久順，龍軍，等. 多產(chǎn)異構(gòu)烷烴的催化裂化工業(yè)技術(shù)開發(fā)與應(yīng)用[J]. 中國(guó)工程科學(xué)，2003，5(5)：55-58

[13] 王千，王成，馮振元，等. K-means 聚類算法研究綜述[J]. 電子設(shè)計(jì)工程，2012，20(7)：21-24

[14] 高新波，謝維信. 模糊聚類理論發(fā)展及應(yīng)用的研究進(jìn)展[J]. 科學(xué)通報(bào)，1999，44(21)：2241-2251

[15] Bezdek J C，Pal N R. Some new indexes of cluster validity [J]. IEEE Transactions on Systems，Man，and Cybernetics，Part B(Cybernetics)，1998，28(3)：301-315.

[16] 于劍，程乾生. 模糊聚類方法中的最佳聚類數(shù)的搜索范圍[J]. 中國(guó)科學(xué)(E輯)，2002，32(2)：274-280

[17] Rezaee M R，Lelieveldt B P，Reiber J H. A new cluster validity index for the fuzzyc-mean[J]. Pattern Recognition Letters，1998，19(3)：237-246

[18] Ruspini E H. A new approach to clustering[J]. Information and Control，1969，15(1)：22-32

[19] Bezdek J C. Clustering validity with fuzzy sets[J]. Mathematical Biology，1974(1)：57-71